Scikit Learn - машины опорных векторов
В этой главе рассматривается метод машинного обучения, называемый машинами опорных векторов (SVM).
Введение
Машины опорных векторов (SVM) - это мощные, но гибкие методы контролируемого машинного обучения, используемые для классификации, регрессии и обнаружения выбросов. SVM очень эффективны в пространствах большой размерности и обычно используются в задачах классификации. SVM популярны и эффективны с точки зрения памяти, потому что они используют подмножество обучающих точек в функции принятия решения.
Основная цель SVM - разделить наборы данных на несколько классов, чтобы найти maximum marginal hyperplane (MMH) что можно сделать в следующие два шага -
Машины опорных векторов сначала будут генерировать гиперплоскости итеративно, что наилучшим образом разделяет классы.
После этого он выберет гиперплоскость, которая правильно разделяет классы.
Некоторые важные концепции в SVM следующие:
Support Vectors- Их можно определить как точки данных, наиболее близкие к гиперплоскости. Опорные векторы помогают определить разделительную линию.
Hyperplane - Плоскость решения или пространство, разделяющее множество объектов разных классов.
Margin - Промежуток между двумя линиями на точках данных шкафа разных классов называется маржей.
Следующие диаграммы дадут вам представление об этих концепциях SVM.
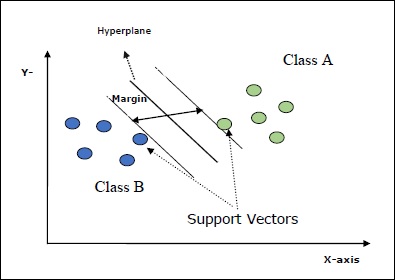
SVM в Scikit-learn поддерживает в качестве входных данных как разреженные, так и плотные выборочные векторы.
Классификация SVM
Scikit-learn предоставляет три класса, а именно: SVC, NuSVC и LinearSVC который может выполнять классификацию мультиклассов.
SVC
Это классификация C-опорных векторов, реализация которой основана на libsvm. Модуль, используемый scikit-learn:sklearn.svm.SVC. Этот класс обрабатывает поддержку мультикласса по схеме «один против одного».
Параметры
В следующей таблице представлены параметры, используемые sklearn.svm.SVC класс -
| Старший Нет | Параметр и описание |
|---|---|
| 1 | C - float, необязательно, по умолчанию = 1.0 Это штрафной параметр члена ошибки. |
| 2 | kernel - строка, необязательно, по умолчанию = 'rbf' Этот параметр указывает тип ядра, которое будет использоваться в алгоритме. мы можем выбрать любой среди,‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’. Значение ядра по умолчанию будет‘rbf’. |
| 3 | degree - int, необязательно, по умолчанию = 3 Он представляет собой степень функции ядра «poly» и будет игнорироваться всеми другими ядрами. |
| 4 | gamma - {'scale', 'auto'} или float, Это коэффициент ядра для ядер "rbf", "poly" и "sigmoid". |
| 5 | optinal default - = 'масштаб' Если вы выберете значение по умолчанию, то есть gamma = 'scale', тогда значение гаммы, которое будет использоваться SVC, будет 1 / (_ ∗. ()). С другой стороны, если gamma = 'auto', используется 1 / _. |
| 6 | coef0 - float, необязательно, по умолчанию = 0,0 Независимый термин в функции ядра, который имеет значение только в 'poly' и 'sigmoid'. |
| 7 | tol - float, необязательно, по умолчанию = 1.e-3 Этот параметр представляет собой критерий остановки для итераций. |
| 8 | shrinking - Логическое значение, необязательно, по умолчанию = True Этот параметр указывает, хотим ли мы использовать эвристику сжатия или нет. |
| 9 | verbose - Boolean, по умолчанию: false Он включает или отключает подробный вывод. Его значение по умолчанию - false. |
| 10 | probability - логическое, необязательное, по умолчанию = true Этот параметр включает или отключает оценки вероятности. Значение по умолчанию - false, но оно должно быть включено перед вызовом fit. |
| 11 | max_iter - int, необязательно, по умолчанию = -1 Как следует из названия, он представляет собой максимальное количество итераций в решателе. Значение -1 означает, что количество итераций не ограничено. |
| 12 | cache_size - поплавок, необязательно Этот параметр указывает размер кеша ядра. Значение будет в МБ (мегабайтах). |
| 13 | random_state - int, экземпляр RandomState или None, необязательно, по умолчанию = none Этот параметр представляет собой начальное число сгенерированного псевдослучайного числа, которое используется при перетасовке данных. Следующие варианты -
|
| 14 | class_weight - {dict, 'сбалансированный'}, необязательно Этот параметр устанавливает для параметра C класса j значение _ℎ [] ∗ для SVC. Если мы используем вариант по умолчанию, это означает, что все классы должны иметь единичный вес. С другой стороны, если вы выберетеclass_weight:balanced, он будет использовать значения y для автоматической настройки весов. |
| 15 | decision_function_shape - ovo ',' ovr ', по умолчанию =' ovr ' Этот параметр решает, вернет ли алгоритм ‘ovr’ (one-vs-rest) решающая функция формы, как и все другие классификаторы, или исходная ovo(один против одного) функция принятия решений libsvm. |
| 16 | break_ties - логическое, необязательное, по умолчанию = false True - Прогноз разорвет связи в соответствии со значениями достоверности solution_function False - Прогноз вернет первый класс среди связанных классов. |
Атрибуты
Следующая таблица содержит атрибуты, используемые sklearn.svm.SVC класс -
| Старший Нет | Атрибуты и описание |
|---|---|
| 1 | support_ - в виде массива, shape = [n_SV] Возвращает индексы опорных векторов. |
| 2 | support_vectors_ - в виде массива, shape = [n_SV, n_features] Он возвращает опорные векторы. |
| 3 | n_support_ - как массив, dtype = int32, shape = [n_class] Он представляет количество опорных векторов для каждого класса. |
| 4 | dual_coef_ - массив, shape = [n_class-1, n_SV] Это коэффициенты опорных векторов в решающей функции. |
| 5 | coef_ - массив, форма = [n_class * (n_class-1) / 2, n_features] Этот атрибут, доступный только в случае линейного ядра, обеспечивает вес, присвоенный функциям. |
| 6 | intercept_ - массив, форма = [n_class * (n_class-1) / 2] Он представляет собой независимый член (константу) в решающей функции. |
| 7 | fit_status_ - int Если он установлен правильно, то на выходе будет 0. Если он установлен неправильно, выход будет 1. |
| 8 | classes_ - массив формы = [n_classes] Он дает метки классов. |
Implementation Example
Как и другие классификаторы, SVC также должен быть оснащен следующими двумя массивами:
Массив Xпроведение обучающих выборок. Он имеет размер [n_samples, n_features].
Массив Yудерживая целевые значения, то есть метки классов для обучающих выборок. Его размер [n_samples].
Следующий скрипт Python использует sklearn.svm.SVC класс -
import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import SVC
SVCClf = SVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
SVCClf.fit(X, y)Output
SVC(C = 1.0, cache_size = 200, class_weight = None, coef0 = 0.0,
decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
max_iter = -1, probability = False, random_state = None, shrinking = False,
tol = 0.001, verbose = False)Example
Теперь, после установки, мы можем получить вектор веса с помощью следующего скрипта Python -
SVCClf.coef_Output
array([[0.5, 0.5]])Example
Точно так же мы можем получить значение других атрибутов следующим образом:
SVCClf.predict([[-0.5,-0.8]])Output
array([1])Example
SVCClf.n_support_Output
array([1, 1])Example
SVCClf.support_vectors_Output
array(
[
[-1., -1.],
[ 1., 1.]
]
)Example
SVCClf.support_Output
array([0, 2])Example
SVCClf.intercept_Output
array([-0.])Example
SVCClf.fit_status_Output
0NuSVC
NuSVC - это классификация опорных векторов Nu. Это еще один класс, предоставляемый scikit-learn, который может выполнять мультиклассовую классификацию. Это похоже на SVC, но NuSVC принимает несколько другие наборы параметров. Параметр, который отличается от SVC, выглядит следующим образом -
nu - float, необязательно, по умолчанию = 0.5
Он представляет собой верхнюю границу доли ошибок обучения и нижнюю границу доли опорных векторов. Его значение должно быть в интервале (o, 1].
Остальные параметры и атрибуты такие же, как у SVC.
Пример реализации
Мы можем реализовать тот же пример, используя sklearn.svm.NuSVC класс тоже.
import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
from sklearn.svm import NuSVC
NuSVCClf = NuSVC(kernel = 'linear',gamma = 'scale', shrinking = False,)
NuSVCClf.fit(X, y)Вывод
NuSVC(cache_size = 200, class_weight = None, coef0 = 0.0,
decision_function_shape = 'ovr', degree = 3, gamma = 'scale', kernel = 'linear',
max_iter = -1, nu = 0.5, probability = False, random_state = None,
shrinking = False, tol = 0.001, verbose = False)Мы можем получить выходные данные остальных атрибутов, как это было в случае с SVC.
LinearSVC
Это классификация линейных опорных векторов. Это похоже на SVC с ядром = 'linear'. Разница между ними в том, чтоLinearSVC реализован в терминах liblinear, в то время как SVC реализован в libsvm. Вот в чем причинаLinearSVCимеет большую гибкость в выборе функций штрафов и потерь. Он также лучше масштабируется для большого количества выборок.
Если говорить о его параметрах и атрибутах, то он не поддерживает ‘kernel’ поскольку предполагается, что он линейный, и ему также не хватает некоторых атрибутов, таких как support_, support_vectors_, n_support_, fit_status_ и, dual_coef_.
Однако он поддерживает penalty и loss параметры следующим образом -
penalty − string, L1 or L2(default = ‘L2’)
Этот параметр используется для указания нормы (L1 или L2), используемой при штрафных санкциях (регуляризации).
loss − string, hinge, squared_hinge (default = squared_hinge)
Он представляет функцию потерь, где «шарнир» - это стандартные потери SVM, а «квадрат_холоста» - это квадрат потерь в шарнире.
Пример реализации
Следующий скрипт Python использует sklearn.svm.LinearSVC класс -
from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
X, y = make_classification(n_features = 4, random_state = 0)
LSVCClf = LinearSVC(dual = False, random_state = 0, penalty = 'l1',tol = 1e-5)
LSVCClf.fit(X, y)Вывод
LinearSVC(C = 1.0, class_weight = None, dual = False, fit_intercept = True,
intercept_scaling = 1, loss = 'squared_hinge', max_iter = 1000,
multi_class = 'ovr', penalty = 'l1', random_state = 0, tol = 1e-05, verbose = 0)пример
Теперь, после подбора, модель может предсказывать новые значения следующим образом:
LSVCClf.predict([[0,0,0,0]])Вывод
[1]пример
В приведенном выше примере мы можем получить вектор веса с помощью следующего скрипта Python:
LSVCClf.coef_Вывод
[[0. 0. 0.91214955 0.22630686]]пример
Точно так же мы можем получить значение перехвата с помощью следующего скрипта Python -
LSVCClf.intercept_Вывод
[0.26860518]Регрессия с SVM
Как обсуждалось ранее, SVM используется для задач классификации и регрессии. Метод классификации опорных векторов (SVC) Scikit-learn также может быть расширен для решения задач регрессии. Этот расширенный метод называется регрессией опорных векторов (SVR).
Основное сходство между SVM и SVR
Модель, созданная SVC, зависит только от подмножества обучающих данных. Почему? Потому что функция затрат для построения модели не заботится о точках данных обучения, которые лежат за пределами поля.
Принимая во внимание, что модель, созданная SVR (регрессия вектора поддержки), также зависит только от подмножества обучающих данных. Почему? Поскольку функция стоимости для построения модели игнорирует любые точки обучающих данных, близкие к предсказанию модели.
Scikit-learn предоставляет три класса, а именно: SVR, NuSVR and LinearSVR как три разные реализации SVR.
СВР
Это векторная регрессия с поддержкой Epsilon, реализация которой основана на libsvm. В отличие отSVC В модели есть два свободных параметра, а именно ‘C’ и ‘epsilon’.
epsilon - float, необязательно, по умолчанию = 0,1
Он представляет собой эпсилон в модели эпсилон-SVR и определяет эпсилон-трубку, внутри которой в функции потерь при обучении не связано никаких штрафов с точками, предсказанными в пределах эпсилон-расстояния от фактического значения.
Остальные параметры и атрибуты аналогичны тем, которые мы использовали в SVC.
Пример реализации
Следующий скрипт Python использует sklearn.svm.SVR класс -
from sklearn import svm
X = [[1, 1], [2, 2]]
y = [1, 2]
SVRReg = svm.SVR(kernel = ’linear’, gamma = ’auto’)
SVRReg.fit(X, y)Вывод
SVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, epsilon = 0.1, gamma = 'auto',
kernel = 'linear', max_iter = -1, shrinking = True, tol = 0.001, verbose = False)пример
Теперь, после установки, мы можем получить вектор веса с помощью следующего скрипта Python -
SVRReg.coef_Вывод
array([[0.4, 0.4]])пример
Точно так же мы можем получить значение других атрибутов следующим образом:
SVRReg.predict([[1,1]])Вывод
array([1.1])Точно так же мы можем получить значения других атрибутов.
NuSVR
NuSVR является Nu Support Vector регрессия. Это похоже на NuSVC, но NuSVR использует параметрnuдля контроля количества опорных векторов. Причем, в отличие от NuSVC, гдеnu заменен параметр C, здесь он заменяет epsilon.
Пример реализации
Следующий скрипт Python использует sklearn.svm.SVR класс -
from sklearn.svm import NuSVR
import numpy as np
n_samples, n_features = 20, 15
np.random.seed(0)
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
NuSVRReg = NuSVR(kernel = 'linear', gamma = 'auto',C = 1.0, nu = 0.1)^M
NuSVRReg.fit(X, y)Вывод
NuSVR(C = 1.0, cache_size = 200, coef0 = 0.0, degree = 3, gamma = 'auto',
kernel = 'linear', max_iter = -1, nu = 0.1, shrinking = True, tol = 0.001,
verbose = False)пример
Теперь, после установки, мы можем получить вектор веса с помощью следующего скрипта Python -
NuSVRReg.coef_Вывод
array(
[
[-0.14904483, 0.04596145, 0.22605216, -0.08125403, 0.06564533,
0.01104285, 0.04068767, 0.2918337 , -0.13473211, 0.36006765,
-0.2185713 , -0.31836476, -0.03048429, 0.16102126, -0.29317051]
]
)Точно так же мы можем получить значение других атрибутов.
LinearSVR
Это линейная регрессия опорных векторов. Это похоже на SVR с ядром = 'linear'. Разница между ними в том, чтоLinearSVR реализовано с точки зрения liblinear, а SVC реализован в libsvm. Вот в чем причинаLinearSVRимеет большую гибкость в выборе функций штрафов и потерь. Он также лучше масштабируется для большого количества выборок.
Если говорить о его параметрах и атрибутах, то он не поддерживает ‘kernel’ поскольку предполагается, что он линейный, и ему также не хватает некоторых атрибутов, таких как support_, support_vectors_, n_support_, fit_status_ и, dual_coef_.
Однако он поддерживает следующие параметры «потери»:
loss - строка, необязательно, по умолчанию = 'epsilon_insensitive'
Он представляет функцию потерь, где epsilon_insensitive loss - это потеря L1, а квадратичная потеря нечувствительности к epsilon - это потеря L2.
Пример реализации
Следующий скрипт Python использует sklearn.svm.LinearSVR класс -
from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression
X, y = make_regression(n_features = 4, random_state = 0)
LSVRReg = LinearSVR(dual = False, random_state = 0,
loss = 'squared_epsilon_insensitive',tol = 1e-5)
LSVRReg.fit(X, y)Вывод
LinearSVR(
C=1.0, dual=False, epsilon=0.0, fit_intercept=True,
intercept_scaling=1.0, loss='squared_epsilon_insensitive',
max_iter=1000, random_state=0, tol=1e-05, verbose=0
)пример
Теперь, после подбора, модель может предсказывать новые значения следующим образом:
LSRReg.predict([[0,0,0,0]])Вывод
array([-0.01041416])пример
В приведенном выше примере мы можем получить вектор веса с помощью следующего скрипта Python:
LSRReg.coef_Вывод
array([20.47354746, 34.08619401, 67.23189022, 87.47017787])пример
Точно так же мы можем получить значение перехвата с помощью следующего скрипта Python -
LSRReg.intercept_Вывод
array([-0.01041416])