SciPy - Краткое руководство
SciPy, произносится как Sigh Pi, представляет собой научный питон с открытым исходным кодом, распространяемый в рамках лицензированной библиотеки BSD для выполнения математических, научных и инженерных вычислений.
Библиотека SciPy зависит от NumPy, который обеспечивает удобные и быстрые манипуляции с N-мерными массивами. Библиотека SciPy создана для работы с массивами NumPy и предоставляет множество удобных и эффективных числовых методов, таких как процедуры для численного интегрирования и оптимизации. Вместе они работают во всех популярных операционных системах, быстро устанавливаются и бесплатны. NumPy и SciPy просты в использовании, но достаточно мощны, чтобы на них могли положиться некоторые ведущие ученые и инженеры мира.
Подпакеты SciPy
SciPy состоит из подпакетов, охватывающих различные области научных вычислений. Они приведены в следующей таблице -
| scipy.cluster | Векторное квантование / Kmeans |
| scipy.constants | Физико-математические константы |
| scipy.fftpack | преобразование Фурье |
| scipy.integrate | Процедуры интеграции |
| scipy.interpolate | Интерполяция |
| scipy.io | Ввод и вывод данных |
| scipy.linalg | Процедуры линейной алгебры |
| scipy.ndimage | пакет n-мерных изображений |
| scipy.odr | Ортогональная дистанционная регрессия |
| scipy.optimize | Оптимизация |
| scipy.signal | Обработка сигналов |
| scipy.sparse | Разреженные матрицы |
| scipy.spatial | Структуры и алгоритмы пространственных данных |
| scipy.special | Любые специальные математические функции |
| scipy.stats | Статистика |
Структура данных
Базовая структура данных, используемая SciPy, представляет собой многомерный массив, предоставляемый модулем NumPy. NumPy предоставляет некоторые функции для линейной алгебры, преобразования Фурье и генерации случайных чисел, но не с общностью эквивалентных функций в SciPy.
Стандартный дистрибутив Python не поставляется в комплекте с каким-либо модулем SciPy. Легкая альтернатива - установить SciPy с помощью популярного установщика пакетов Python,
pip install pandasЕсли мы установим Anaconda Python package, Панды будут установлены по умолчанию. Ниже приведены пакеты и ссылки для их установки в различных операционных системах.
Windows
Anaconda (из https://www.continuum.io) - это бесплатный дистрибутив Python для стека SciPy. Он также доступен для Linux и Mac.
Canopy (https://www.enthought.com/products/canopy/) доступен бесплатно, а также для коммерческого распространения с полным стеком SciPy для Windows, Linux и Mac.
Python (x,y)- Это бесплатный дистрибутив Python со стеком SciPy и Spyder IDE для ОС Windows. (Можно загрузить сhttps://python-xy.github.io/)
Linux
Менеджеры пакетов соответствующих дистрибутивов Linux используются для установки одного или нескольких пакетов в стек SciPy.
Ubuntu
Мы можем использовать следующий путь для установки Python в Ubuntu.
sudo apt-get install python-numpy python-scipy
python-matplotlibipythonipython-notebook python-pandas python-sympy python-noseFedora
Мы можем использовать следующий путь для установки Python в Fedora.
sudo yum install numpyscipy python-matplotlibipython python-pandas
sympy python-nose atlas-develПо умолчанию все функции NumPy доступны через пространство имен SciPy. При импорте SciPy нет необходимости явно импортировать функции NumPy. Главный объект NumPy - это однородный многомерный массив. Это таблица элементов (обычно чисел) одного типа, проиндексированных набором положительных целых чисел. В NumPy размеры называются осями. Номерaxes называется как rank.
Теперь давайте пересмотрим базовую функциональность векторов и матриц в NumPy. Поскольку SciPy построен на основе массивов NumPy, необходимо понимание основ NumPy. Поскольку большинство разделов линейной алгебры имеет дело только с матрицами.
NumPy Вектор
Вектор можно создать несколькими способами. Некоторые из них описаны ниже.
Преобразование объектов Python, подобных массиву, в NumPy
Рассмотрим следующий пример.
import numpy as np
list = [1,2,3,4]
arr = np.array(list)
print arrРезультат вышеупомянутой программы будет следующим.
[1 2 3 4]Внутреннее создание массива NumPy
NumPy имеет встроенные функции для создания массивов с нуля. Некоторые из этих функций описаны ниже.
Использование нулей ()
Функция нулей (форма) создаст массив, заполненный значениями 0 с указанной формой. По умолчанию dtype - float64. Рассмотрим следующий пример.
import numpy as np
print np.zeros((2, 3))Результат вышеупомянутой программы будет следующим.
array([[ 0., 0., 0.],
[ 0., 0., 0.]])Используя единицы ()
Функция ones (shape) создаст массив, заполненный 1 значениями. Во всем остальном он идентичен нулям. Рассмотрим следующий пример.
import numpy as np
print np.ones((2, 3))Результат вышеупомянутой программы будет следующим.
array([[ 1., 1., 1.],
[ 1., 1., 1.]])Использование arange ()
Функция arange () создает массивы с регулярно увеличивающимися значениями. Рассмотрим следующий пример.
import numpy as np
print np.arange(7)Вышеупомянутая программа сгенерирует следующий вывод.
array([0, 1, 2, 3, 4, 5, 6])Определение типа данных значений
Рассмотрим следующий пример.
import numpy as np
arr = np.arange(2, 10, dtype = np.float)
print arr
print "Array Data Type :",arr.dtypeВышеупомянутая программа сгенерирует следующий вывод.
[ 2. 3. 4. 5. 6. 7. 8. 9.]
Array Data Type : float64Использование linspace ()
Функция linspace () создаст массивы с указанным количеством элементов, которые будут равномерно распределены между указанными начальным и конечным значениями. Рассмотрим следующий пример.
import numpy as np
print np.linspace(1., 4., 6)Вышеупомянутая программа сгенерирует следующий вывод.
array([ 1. , 1.6, 2.2, 2.8, 3.4, 4. ])Матрица
Матрица - это специализированный двумерный массив, который сохраняет свою двумерную природу посредством операций. Он имеет определенные специальные операторы, такие как * (умножение матриц) и ** (степень матрицы). Рассмотрим следующий пример.
import numpy as np
print np.matrix('1 2; 3 4')Вышеупомянутая программа сгенерирует следующий вывод.
matrix([[1, 2],
[3, 4]])Сопряженное транспонирование матрицы
Эта функция возвращает (сложное) сопряженное транспонирование self. Рассмотрим следующий пример.
import numpy as np
mat = np.matrix('1 2; 3 4')
print mat.HВышеупомянутая программа сгенерирует следующий вывод.
matrix([[1, 3],
[2, 4]])Транспонировать матрицу
Эта функция возвращает транспонирование себя. Рассмотрим следующий пример.
import numpy as np
mat = np.matrix('1 2; 3 4')
mat.TВышеупомянутая программа сгенерирует следующий вывод.
matrix([[1, 3],
[2, 4]])Когда мы транспонируем матрицу, мы создаем новую матрицу, строки которой являются столбцами оригинала. С другой стороны, сопряженная транспозиция меняет местами строку и индекс столбца для каждого элемента матрицы. Обращение к матрице - это матрица, которая при умножении на исходную матрицу дает единичную матрицу.
K-means clustering- это метод поиска кластеров и центров кластеров в наборе данных без метки. Интуитивно мы могли бы думать о кластере как о группе точек данных, расстояния между точками которых малы по сравнению с расстояниями до точек за пределами кластера. Учитывая начальный набор из K центров, алгоритм K-средних повторяет следующие два шага:
Для каждого центра определяется подмножество тренировочных точек (его кластер), которое ближе к нему, чем к любому другому центру.
Вычисляется среднее значение каждой функции для точек данных в каждом кластере, и этот средний вектор становится новым центром для этого кластера.
Эти два шага повторяются до тех пор, пока центры не перестанут двигаться или назначения больше не изменятся. Затем новая точкаxможет быть отнесен к кластеру ближайшего прототипа. Библиотека SciPy обеспечивает хорошую реализацию алгоритма K-средних посредством кластерного пакета. Давайте разберемся, как им пользоваться.
Реализация K-средних в SciPy
Мы поймем, как реализовать K-Means в SciPy.
Импорт K-средних
Мы увидим реализацию и использование каждой импортированной функции.
from SciPy.cluster.vq import kmeans,vq,whitenГенерация данных
Нам нужно смоделировать некоторые данные, чтобы изучить кластеризацию.
from numpy import vstack,array
from numpy.random import rand
# data generation with three features
data = vstack((rand(100,3) + array([.5,.5,.5]),rand(100,3)))Теперь нам нужно проверить данные. Вышеупомянутая программа сгенерирует следующий вывод.
array([[ 1.48598868e+00, 8.17445796e-01, 1.00834051e+00],
[ 8.45299768e-01, 1.35450732e+00, 8.66323621e-01],
[ 1.27725864e+00, 1.00622682e+00, 8.43735610e-01],
…………….Нормализовать группу наблюдений для каждой функции. Перед запуском K-средних полезно изменить масштаб каждого измерения объекта наблюдения с помощью отбеливания. Каждую особенность делят на ее стандартное отклонение по всем наблюдениям, чтобы получить единичную дисперсию.
Отбелить данные
Мы должны использовать следующий код, чтобы осветлить данные.
# whitening of data
data = whiten(data)Вычислить K-средние с тремя кластерами
Давайте теперь вычислим K-Means с тремя кластерами, используя следующий код.
# computing K-Means with K = 3 (2 clusters)
centroids,_ = kmeans(data,3)Приведенный выше код выполняет K-средние для набора векторов наблюдения, образующих K кластеров. Алгоритм K-средних регулирует центроиды до тех пор, пока не будет достигнут достаточный прогресс, т. Е. Изменение искажения, поскольку последняя итерация меньше некоторого порога. Здесь мы можем наблюдать центроид кластера, распечатав переменную центроидов, используя приведенный ниже код.
print(centroids)Приведенный выше код сгенерирует следующий вывод.
print(centroids)[ [ 2.26034702 1.43924335 1.3697022 ]
[ 2.63788572 2.81446462 2.85163854]
[ 0.73507256 1.30801855 1.44477558] ]Назначьте каждое значение кластеру, используя приведенный ниже код.
# assign each sample to a cluster
clx,_ = vq(data,centroids)В vq функция сравнивает каждый вектор наблюдения в 'M' на 'N' obsмассив с центроидами и назначает наблюдение ближайшему кластеру. Он возвращает кластер каждого наблюдения и искажения. Мы также можем проверить искажение. Давайте проверим кластер каждого наблюдения, используя следующий код.
# check clusters of observation
print clxПриведенный выше код сгенерирует следующий вывод.
array([1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 2, 0, 2, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0,
0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 0,
2, 2, 2, 1, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2], dtype=int32)Различные значения 0, 1, 2 указанного выше массива указывают на кластеры.
Пакет констант SciPy предоставляет широкий спектр констант, которые используются в общей научной области.
Пакет констант SciPy
В scipy.constants packageпредоставляет различные константы. Мы должны импортировать необходимые константы и использовать их в соответствии с требованиями. Давайте посмотрим, как эти постоянные переменные импортируются и используются.
Для начала давайте сравним значение «пи», рассмотрев следующий пример.
#Import pi constant from both the packages
from scipy.constants import pi
from math import pi
print("sciPy - pi = %.16f"%scipy.constants.pi)
print("math - pi = %.16f"%math.pi)Вышеупомянутая программа сгенерирует следующий вывод.
sciPy - pi = 3.1415926535897931
math - pi = 3.1415926535897931Список доступных констант
В следующих таблицах кратко описаны различные константы.
Математические константы
| Sr. No. | Постоянный | Описание |
|---|---|---|
| 1 | Пи | Пи |
| 2 | золотой | Золотое сечение |
Физические константы
В следующей таблице перечислены наиболее часто используемые физические константы.
| Sr. No. | Константа и описание |
|---|---|
| 1 | c Скорость света в вакууме |
| 2 | speed_of_light Скорость света в вакууме |
| 3 | h Постоянная Планка |
| 4 | Planck Постоянная Планка h |
| 5 | G Гравитационная постоянная Ньютона |
| 6 | e Элементарный заряд |
| 7 | R Молярная газовая постоянная |
| 8 | Avogadro Константа Авогадро |
| 9 | k Постоянная Больцмана |
| 10 | electron_mass(OR) m_e Электронная масса |
| 11 | proton_mass (OR) m_p Масса протона |
| 12 | neutron_mass(OR)m_n Масса нейтрона |
Единицы
В следующей таблице приведен список единиц СИ.
| Sr. No. | Единица измерения | Значение |
|---|---|---|
| 1 | Милли | 0,001 |
| 2 | микро | 1e-06 |
| 3 | килограмм | 1000 |
Эти единицы варьируются от йотта, дзетта, экса, пета, тера …… килограмм, гектор,… нано, пико,… до зепто.
Другие важные константы
В следующей таблице перечислены другие важные константы, используемые в SciPy.
| Sr. No. | Единица измерения | Значение |
|---|---|---|
| 1 | грамм | 0,001 кг |
| 2 | атомная масса | Постоянная атомной массы |
| 3 | степень | Градус в радианах |
| 4 | минута | Одна минута в секундах |
| 5 | день | Один день за секунды |
| 6 | дюйм | Один дюйм в метрах |
| 7 | микрон | Один микрон в метрах |
| 8 | световой год | Один световой год в метрах |
| 9 | банкомат | Стандартная атмосфера в паскалях |
| 10 | акр | Один акр в квадратных метрах |
| 11 | литр | Один литр в кубических метрах |
| 12 | галлон | Один галлон в кубических метрах |
| 13 | км / ч | Километры в час в метрах в секунду |
| 14 | градус Фаренгейта | Один Фаренгейт в Кельвинах |
| 15 | эВ | Один электрон-вольт в джоулях |
| 16 | л.с. | Одна лошадиная сила в ваттах |
| 17 | дин | Один дин в ньютонах |
| 18 | lambda2nu | Преобразовать длину волны в оптическую частоту |
Запоминать все это довольно сложно. Легкий способ узнать, какая клавиша для какой функции находится сscipy.constants.find()метод. Рассмотрим следующий пример.
import scipy.constants
res = scipy.constants.physical_constants["alpha particle mass"]
print resВышеупомянутая программа сгенерирует следующий вывод.
[
'alpha particle mass',
'alpha particle mass energy equivalent',
'alpha particle mass energy equivalent in MeV',
'alpha particle mass in u',
'electron to alpha particle mass ratio'
]Этот метод возвращает список ключей, иначе ничего, если ключевое слово не совпадает.
Fourier Transformationвычисляется на сигнале временной области, чтобы проверить его поведение в частотной области. Преобразование Фурье находит свое применение в таких дисциплинах, как обработка сигналов и шумов, обработка изображений, обработка аудиосигналов и т. Д. SciPy предлагает модуль fftpack, который позволяет пользователю вычислять быстрые преобразования Фурье.
Ниже приведен пример синусоидальной функции, которая будет использоваться для вычисления преобразования Фурье с использованием модуля fftpack.
Быстрое преобразование Фурье
Давайте разберемся, что такое быстрое преобразование Фурье подробнее.
Одномерное дискретное преобразование Фурье
БПФ y [k] длины N последовательности x [n] длины N вычисляется с помощью fft (), а обратное преобразование вычисляется с помощью ifft (). Рассмотрим следующий пример
#Importing the fft and inverse fft functions from fftpackage
from scipy.fftpack import fft
#create an array with random n numbers
x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
#Applying the fft function
y = fft(x)
print yВышеупомянутая программа сгенерирует следующий вывод.
[ 4.50000000+0.j 2.08155948-1.65109876j -1.83155948+1.60822041j
-1.83155948-1.60822041j 2.08155948+1.65109876j ]Давайте посмотрим на другой пример
#FFT is already in the workspace, using the same workspace to for inverse transform
yinv = ifft(y)
print yinvВышеупомянутая программа сгенерирует следующий вывод.
[ 1.0+0.j 2.0+0.j 1.0+0.j -1.0+0.j 1.5+0.j ]В scipy.fftpackмодуль позволяет вычислять быстрые преобразования Фурье. В качестве иллюстрации (зашумленный) входной сигнал может выглядеть следующим образом:
import numpy as np
time_step = 0.02
period = 5.
time_vec = np.arange(0, 20, time_step)
sig = np.sin(2 * np.pi / period * time_vec) + 0.5 *np.random.randn(time_vec.size)
print sig.sizeСоздаем сигнал с временным шагом 0,02 секунды. Последний оператор печатает размер сигнала. Результат будет следующим -
1000Мы не знаем частоту сигнала; нам известен только временной шаг дискретизации сигнала sig. Предполагается, что сигнал поступает от реальной функции, поэтому преобразование Фурье будет симметричным. Вscipy.fftpack.fftfreq() функция будет генерировать частоты дискретизации и scipy.fftpack.fft() вычислит быстрое преобразование Фурье.
Разберемся в этом на примере.
from scipy import fftpack
sample_freq = fftpack.fftfreq(sig.size, d = time_step)
sig_fft = fftpack.fft(sig)
print sig_fftВышеупомянутая программа сгенерирует следующий вывод.
array([
25.45122234 +0.00000000e+00j, 6.29800973 +2.20269471e+00j,
11.52137858 -2.00515732e+01j, 1.08111300 +1.35488579e+01j,
…….])Дискретное косинусное преобразование
А Discrete Cosine Transform (DCT)выражает конечную последовательность точек данных в виде суммы функций косинуса, колеблющихся на разных частотах. SciPy предоставляет DCT с функциейdct и соответствующий IDCT с функцией idct. Рассмотрим следующий пример.
from scipy.fftpack import dct
print dct(np.array([4., 3., 5., 10., 5., 3.]))Вышеупомянутая программа сгенерирует следующий вывод.
array([ 60., -3.48476592, -13.85640646, 11.3137085, 6., -6.31319305])Обратное дискретное косинусное преобразование восстанавливает последовательность из ее коэффициентов дискретного косинусного преобразования (DCT). Функция idct является обратной функцией dct. Давайте разберемся в этом на следующем примере.
from scipy.fftpack import dct
print idct(np.array([4., 3., 5., 10., 5., 3.]))Вышеупомянутая программа сгенерирует следующий вывод.
array([ 39.15085889, -20.14213562, -6.45392043, 7.13341236,
8.14213562, -3.83035081])Когда функция не может быть интегрирована аналитически или ее очень сложно интегрировать аналитически, обычно обращаются к методам численного интегрирования. SciPy имеет ряд процедур для выполнения численного интегрирования. Большинство из них находится в одномscipy.integrateбиблиотека. В следующей таблице перечислены некоторые часто используемые функции.
| Sr Нет. | Описание функции |
|---|---|
| 1 | quad Единая интеграция |
| 2 | dblquad Двойная интеграция |
| 3 | tplquad Тройная интеграция |
| 4 | nquad n- кратная множественная интеграция |
| 5 | fixed_quad Квадратура Гаусса, порядок n |
| 6 | quadrature Квадратура Гаусса с допуском |
| 7 | romberg Интеграция Ромберга |
| 8 | trapz Трапецеидальная линейка |
| 9 | cumtrapz Правило трапеции для кумулятивного вычисления интеграла |
| 10 | simps Правило Симпсона |
| 11 | romb Интеграция Ромберга |
| 12 | polyint Аналитическое полиномиальное интегрирование (NumPy) |
| 13 | poly1d Вспомогательная функция для polyint (NumPy) |
Отдельные интегралы
Функция Quad - это рабочая лошадка функций интеграции SciPy. Численное интегрирование иногда называютquadrature, отсюда и название. Обычно это выбор по умолчанию для выполнения единичных интегралов функции f (x) в заданном фиксированном диапазоне от a до b.
$$\int_{a}^{b} f(x)dx$$
Общий вид квадрата: scipy.integrate.quad(f, a, b), Где «f» - имя интегрируемой функции. Принимая во внимание, что «a» и «b» - это нижний и верхний пределы соответственно. Давайте посмотрим на пример функции Гаусса, интегрированной в диапазоне от 0 до 1.
Сначала нам нужно определить функцию → $f(x) = e^{-x^2}$ , это можно сделать с помощью лямбда-выражения, а затем вызвать метод quad для этой функции.
import scipy.integrate
from numpy import exp
f= lambda x:exp(-x**2)
i = scipy.integrate.quad(f, 0, 1)
print iВышеупомянутая программа сгенерирует следующий вывод.
(0.7468241328124271, 8.291413475940725e-15)Функция quad возвращает два значения, в которых первое число - это значение интеграла, а второе значение - оценка абсолютной ошибки в значении интеграла.
Note- Поскольку для quad требуется функция в качестве первого аргумента, мы не можем напрямую передать exp в качестве аргумента. Функция Quad принимает в качестве пределов положительную и отрицательную бесконечность. Функция Quad может интегрировать стандартные предопределенные функции NumPy одной переменной, такие как exp, sin и cos.
Кратные интегралы
Механика двойной и тройной интеграции объединена в функции dblquad, tplquad и nquad. Эти функции объединяют четыре или шесть аргументов соответственно. Пределы всех внутренних интегралов должны быть определены как функции.
Двойные интегралы
Общая форма dblquadэто scipy.integrate.dblquad (func, a, b, gfun, hfun). Где func - это имя интегрируемой функции, 'a' и 'b' - это нижний и верхний пределы переменной x, соответственно, а gfun и hfun - имена функций, которые определяют нижний и верхний пределы. переменной y.
В качестве примера воспользуемся методом двойного интеграла.
$$\int_{0}^{1/2} dy \int_{0}^{\sqrt{1-4y^2}} 16xy \:dx$$
Мы определяем функции f, g и h, используя лямбда-выражения. Обратите внимание, что даже если g и h являются константами, как они могут быть во многих случаях, они должны быть определены как функции, как мы сделали здесь для нижнего предела.
import scipy.integrate
from numpy import exp
from math import sqrt
f = lambda x, y : 16*x*y
g = lambda x : 0
h = lambda y : sqrt(1-4*y**2)
i = scipy.integrate.dblquad(f, 0, 0.5, g, h)
print iВышеупомянутая программа сгенерирует следующий вывод.
(0.5, 1.7092350012594845e-14)В дополнение к процедурам, описанным выше, scipy.integrate имеет ряд других подпрограмм интеграции, включая nquad, который выполняет n-кратную множественную интеграцию, а также другие подпрограммы, реализующие различные алгоритмы интеграции. Однако quad и dblquad удовлетворит большинство наших потребностей в численном интегрировании.
В этой главе мы обсудим, как интерполяция помогает в SciPy.
Что такое интерполяция?
Интерполяция - это процесс нахождения значения между двумя точками на линии или кривой. Чтобы помочь нам запомнить, что это означает, мы должны думать о первой части слова «интер» как о значении «вводить», что напоминает нам о том, чтобы заглянуть «внутрь» данных, которые у нас были изначально. Этот инструмент, интерполяция, полезен не только в статистике, но также полезен в науке, бизнесе или когда необходимо предсказать значения, которые попадают в две существующие точки данных.
Давайте создадим некоторые данные и посмотрим, как эту интерполяцию можно выполнить с помощью scipy.interpolate пакет.
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(0, 4, 12)
y = np.cos(x**2/3+4)
print x,yВышеупомянутая программа сгенерирует следующий вывод.
(
array([0., 0.36363636, 0.72727273, 1.09090909, 1.45454545, 1.81818182,
2.18181818, 2.54545455, 2.90909091, 3.27272727, 3.63636364, 4.]),
array([-0.65364362, -0.61966189, -0.51077021, -0.31047698, -0.00715476,
0.37976236, 0.76715099, 0.99239518, 0.85886263, 0.27994201,
-0.52586509, -0.99582185])
)Теперь у нас есть два массива. Предполагая, что эти два массива являются двумя измерениями точек в пространстве, давайте построим график с помощью следующей программы и посмотрим, как они выглядят.
plt.plot(x, y,’o’)
plt.show()Вышеупомянутая программа сгенерирует следующий вывод.
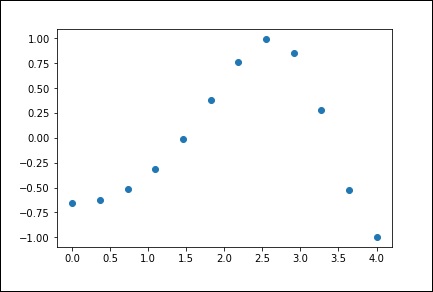
1-D интерполяция
Класс interp1d в scipy.interpolate - это удобный метод для создания функции на основе фиксированных точек данных, которая может быть оценена в любом месте в пределах домена, определенного данными данными, с использованием линейной интерполяции.
Используя приведенные выше данные, давайте создадим функцию интерполяции и нарисуем новый интерполированный график.
f1 = interp1d(x, y,kind = 'linear')
f2 = interp1d(x, y, kind = 'cubic')Используя функцию interp1d, мы создали две функции f1 и f2. Эти функции для заданного входа x возвращают y. Третий вид переменных представляет тип метода интерполяции. «Линейный», «Ближайший», «Нулевой», «Линейный», «Квадратичный», «Кубический» - это несколько методов интерполяции.
Теперь давайте создадим новый ввод большей длины, чтобы увидеть четкую разницу в интерполяции. Мы будем использовать ту же функцию старых данных для новых данных.
xnew = np.linspace(0, 4,30)
plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best')
plt.show()Вышеупомянутая программа сгенерирует следующий вывод.
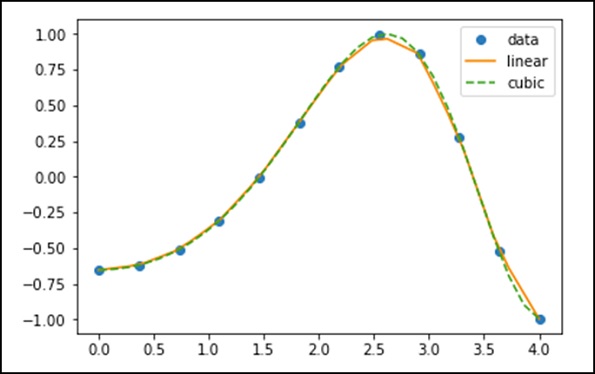
Сплайны
Чтобы рисовать плавные кривые через точки данных, рисовальщики когда-то использовали тонкие гибкие полосы из дерева, твердой резины, металла или пластика, называемые механическими шлицами. Чтобы использовать механический шлиц, штифты помещались в разумный выбор точек вдоль кривой в конструкции, а затем шлицы изгибались так, чтобы касаться каждого из этих штифтов.
Ясно, что при такой конструкции сплайн интерполирует кривую на этих выводах. Его можно использовать для воспроизведения кривой на других чертежах. Точки расположения штифтов называются узлами. Мы можем изменить форму кривой, определяемой сплайном, отрегулировав расположение узлов.
Одномерный сплайн
Одномерный сплайн сглаживания соответствует заданному набору точек данных. Класс UnivariateSpline в scipy.interpolate - это удобный метод для создания функции на основе класса фиксированных точек данных - scipy.interpolate.UnivariateSpline (x, y, w = None, bbox = [None, None], k = 3, s = Нет, ext = 0, check_finite = False).
Parameters - Ниже приведены параметры одномерного сплайна.
Это соответствует сплайну y = spl (x) степени k к предоставленным данным x, y.
'w' - указывает веса для подгонки сплайна. Должен быть положительным. Если нет (по умолчанию), все веса равны.
's' - указывает количество узлов, задавая условие сглаживания.
'k' - Степень сглаживания сплайна. Должно быть <= 5. По умолчанию k = 3, кубический сплайн.
Ext - управляет режимом экстраполяции для элементов, не попадающих в интервал, определенный последовательностью узлов.
если ext = 0 или 'extrapolate', возвращает экстраполированное значение.
если ext = 1 или 'ноль', возвращает 0
если ext = 2 или 'raise', вызывает ValueError
если ext = 3 из 'const', возвращает граничное значение.
check_finite - следует ли проверять, что входные массивы содержат только конечные числа.
Рассмотрим следующий пример.
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
x = np.linspace(-3, 3, 50)
y = np.exp(-x**2) + 0.1 * np.random.randn(50)
plt.plot(x, y, 'ro', ms = 5)
plt.show()Используйте значение по умолчанию для параметра сглаживания.
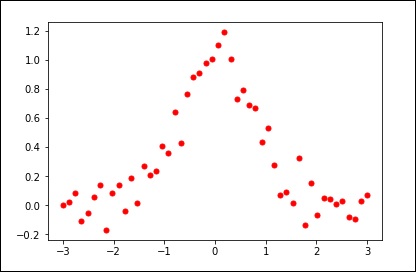
spl = UnivariateSpline(x, y)
xs = np.linspace(-3, 3, 1000)
plt.plot(xs, spl(xs), 'g', lw = 3)
plt.show()Вручную измените степень сглаживания.
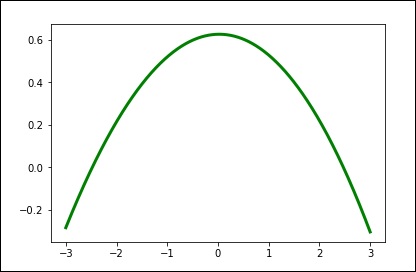
spl.set_smoothing_factor(0.5)
plt.plot(xs, spl(xs), 'b', lw = 3)
plt.show()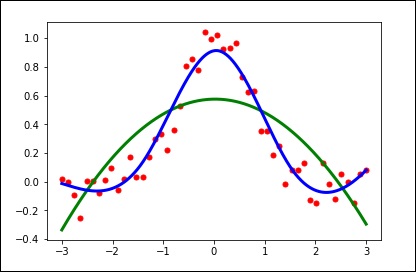
Пакет Scipy.io (ввод и вывод) предоставляет широкий спектр функций для работы с разными форматами файлов. Некоторые из этих форматов -
- Matlab
- IDL
- Матричный рынок
- Wave
- Arff
- Netcdf и др.
Давайте подробно обсудим наиболее часто используемые форматы файлов -
MATLAB
Ниже приведены функции, используемые для загрузки и сохранения файла .mat.
| Sr. No. | Описание функции |
|---|---|
| 1 | loadmat Загружает файл MATLAB |
| 2 | savemat Сохраняет файл MATLAB |
| 3 | whosmat Перечисляет переменные внутри файла MATLAB |
Рассмотрим следующий пример.
import scipy.io as sio
import numpy as np
#Save a mat file
vect = np.arange(10)
sio.savemat('array.mat', {'vect':vect})
#Now Load the File
mat_file_content = sio.loadmat(‘array.mat’)
Print mat_file_contentВышеупомянутая программа сгенерирует следующий вывод.
{
'vect': array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]), '__version__': '1.0',
'__header__': 'MATLAB 5.0 MAT-file Platform: posix, Created on: Sat Sep 30
09:49:32 2017', '__globals__': []
}Мы можем видеть массив вместе с метаинформацией. Если мы хотим проверить содержимое файла MATLAB без чтения данных в память, используйтеwhosmat command как показано ниже.
import scipy.io as sio
mat_file_content = sio.whosmat(‘array.mat’)
print mat_file_contentВышеупомянутая программа сгенерирует следующий вывод.
[('vect', (1, 10), 'int64')]SciPy построен с использованием оптимизированной ATLAS LAPACK и BLASбиблиотеки. Он имеет очень быстрые возможности линейной алгебры. Все эти процедуры линейной алгебры ожидают объект, который можно преобразовать в двумерный массив. Результатом работы этих подпрограмм также является двумерный массив.
SciPy.linalg против NumPy.linalg
Scipy.linalg содержит все функции, которые находятся в numpy.linalg. Кроме того, scipy.linalg также имеет некоторые другие расширенные функции, которых нет в numpy.linalg. Еще одно преимущество использования scipy.linalg перед numpy.linalg заключается в том, что он всегда компилируется с поддержкой BLAS / LAPACK, а для NumPy это необязательно. Следовательно, версия SciPy может быть быстрее в зависимости от того, как был установлен NumPy.
Линейные уравнения
В scipy.linalg.solve Функция решает линейное уравнение a * x + b * y = Z для неизвестных значений x, y.
В качестве примера предположим, что требуется решить следующие одновременные уравнения.
x + 3y + 5z = 10
2x + 5y + z = 8
2x + 3y + 8z = 3
Чтобы решить приведенное выше уравнение для значений x, y, z, мы можем найти вектор решения, используя обратную матрицу, как показано ниже.
$$\begin{bmatrix} x\\ y\\ z \end{bmatrix} = \begin{bmatrix} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8 \end{bmatrix}^{-1} \begin{bmatrix} 10\\ 8\\ 3 \end{bmatrix} = \frac{1}{25} \begin{bmatrix} -232\\ 129\\ 19 \end{bmatrix} = \begin{bmatrix} -9.28\\ 5.16\\ 0.76 \end{bmatrix}.$$
Однако лучше использовать linalg.solve команда, которая может быть быстрее и численно стабильнее.
Функция решения принимает два входных параметра «a» и «b», в которых «a» представляет коэффициенты, а «b» представляет соответствующее значение правой части и возвращает массив решений.
Рассмотрим следующий пример.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy arrays
a = np.array([[3, 2, 0], [1, -1, 0], [0, 5, 1]])
b = np.array([2, 4, -1])
#Passing the values to the solve function
x = linalg.solve(a, b)
#printing the result array
print xВышеупомянутая программа сгенерирует следующий вывод.
array([ 2., -2., 9.])В поисках детерминанта
Определитель квадратной матрицы A часто обозначается как | A | и - величина, часто используемая в линейной алгебре. В SciPy это вычисляется с использованиемdet()функция. Он принимает на вход матрицу и возвращает скалярное значение.
Рассмотрим следующий пример.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the det function
x = linalg.det(A)
#printing the result
print xВышеупомянутая программа сгенерирует следующий вывод.
-2.0Собственные значения и собственные векторы
Задача собственное значение-собственный вектор - одна из наиболее часто используемых операций линейной алгебры. Мы можем найти собственные значения (λ) и соответствующие собственные векторы (v) квадратной матрицы (A), учитывая следующее соотношение -
Av = λv
scipy.linalg.eigвычисляет собственные значения из обычной или обобщенной задачи на собственные значения. Эта функция возвращает собственные значения и собственные векторы.
Рассмотрим следующий пример.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the eig function
l, v = linalg.eig(A)
#printing the result for eigen values
print l
#printing the result for eigen vectors
print vВышеупомянутая программа сгенерирует следующий вывод.
array([-0.37228132+0.j, 5.37228132+0.j]) #--Eigen Values
array([[-0.82456484, -0.41597356], #--Eigen Vectors
[ 0.56576746, -0.90937671]])Разложение по сингулярным значениям
Разложение по сингулярным значениям (SVD) можно рассматривать как расширение проблемы собственных значений на матрицы, которые не являются квадратными.
В scipy.linalg.svd факторизует матрицу 'a' на две унитарные матрицы 'U' и 'Vh' и одномерный массив 's' сингулярных значений (действительных, неотрицательных), так что a == U * S * Vh, где 'S 'представляет собой матрицу нулей подходящей формы с главной диагональю' s '.
Рассмотрим следующий пример.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
a = np.random.randn(3, 2) + 1.j*np.random.randn(3, 2)
#Passing the values to the eig function
U, s, Vh = linalg.svd(a)
# printing the result
print U, Vh, sВышеупомянутая программа сгенерирует следующий вывод.
(
array([
[ 0.54828424-0.23329795j, -0.38465728+0.01566714j,
-0.18764355+0.67936712j],
[-0.27123194-0.5327436j , -0.57080163-0.00266155j,
-0.39868941-0.39729416j],
[ 0.34443818+0.4110186j , -0.47972716+0.54390586j,
0.25028608-0.35186815j]
]),
array([ 3.25745379, 1.16150607]),
array([
[-0.35312444+0.j , 0.32400401+0.87768134j],
[-0.93557636+0.j , -0.12229224-0.33127251j]
])
)Подмодуль SciPy ndimage предназначен для обработки изображений. Здесь ndimage означает n-мерное изображение.
Вот некоторые из наиболее распространенных задач обработки изображений: & miuns;
- Ввод / вывод, отображение изображений
- Основные манипуляции - кадрирование, переворачивание, поворот и т. Д.
- Фильтрация изображений - уменьшение шума, повышение резкости и т. Д.
- Сегментация изображения - маркировка пикселей, соответствующих различным объектам
- Classification
- Извлечение признаков
- Registration
Давайте обсудим, как некоторых из них можно достичь с помощью SciPy.
Открытие и запись в файлы изображений
В misc packageв SciPy есть несколько изображений. Мы используем эти изображения для изучения манипуляций с изображениями. Рассмотрим следующий пример.
from scipy import misc
f = misc.face()
misc.imsave('face.png', f) # uses the Image module (PIL)
import matplotlib.pyplot as plt
plt.imshow(f)
plt.show()Вышеупомянутая программа сгенерирует следующий вывод.

Любые изображения в исходном формате представляют собой комбинацию цветов, представленных числами в матричном формате. Машина понимает изображения и манипулирует ими только на основе этих чисел. RGB - популярный способ представления.
Давайте посмотрим статистическую информацию на изображении выше.
from scipy import misc
face = misc.face(gray = False)
print face.mean(), face.max(), face.min()Вышеупомянутая программа сгенерирует следующий вывод.
110.16274388631184, 255, 0Теперь мы знаем, что изображение состоит из чисел, поэтому любое изменение значения числа изменяет исходное изображение. Выполним геометрические преобразования изображения. Основная геометрическая операция - обрезка
from scipy import misc
face = misc.face(gray = True)
lx, ly = face.shape
# Cropping
crop_face = face[lx / 4: - lx / 4, ly / 4: - ly / 4]
import matplotlib.pyplot as plt
plt.imshow(crop_face)
plt.show()Вышеупомянутая программа сгенерирует следующий вывод.
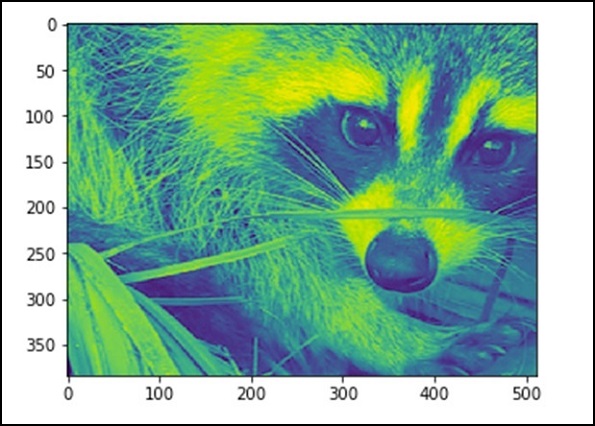
Мы также можем выполнить некоторые базовые операции, такие как перевернуть изображение вверх ногами, как описано ниже.
# up <-> down flip
from scipy import misc
face = misc.face()
flip_ud_face = np.flipud(face)
import matplotlib.pyplot as plt
plt.imshow(flip_ud_face)
plt.show()Вышеупомянутая программа сгенерирует следующий вывод.

Помимо этого, у нас есть rotate() function, который поворачивает изображение на заданный угол.
# rotation
from scipy import misc,ndimage
face = misc.face()
rotate_face = ndimage.rotate(face, 45)
import matplotlib.pyplot as plt
plt.imshow(rotate_face)
plt.show()Вышеупомянутая программа сгенерирует следующий вывод.
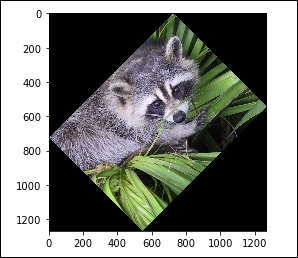
Фильтры
Давайте обсудим, как фильтры помогают в обработке изображений.
Что такое фильтрация при обработке изображений?
Фильтрация - это метод изменения или улучшения изображения. Например, вы можете отфильтровать изображение, чтобы выделить определенные особенности или удалить другие особенности. Операции обработки изображений, реализованные с помощью фильтрации, включают сглаживание, повышение резкости и улучшение краев.
Фильтрация - это операция соседства, в которой значение любого заданного пикселя в выходном изображении определяется путем применения некоторого алгоритма к значениям пикселей в окрестности соответствующего входного пикселя. Давайте теперь выполним несколько операций с помощью SciPy ndimage.
Размытие
Размытие широко используется для уменьшения шума на изображении. Мы можем выполнить операцию фильтрации и увидеть изменение изображения. Рассмотрим следующий пример.
from scipy import misc
face = misc.face()
blurred_face = ndimage.gaussian_filter(face, sigma=3)
import matplotlib.pyplot as plt
plt.imshow(blurred_face)
plt.show()Вышеупомянутая программа сгенерирует следующий вывод.

Значение сигмы указывает уровень размытия по пятибалльной шкале. Мы можем увидеть изменение качества изображения, настроив значение сигмы. Для получения дополнительных сведений о размытии щелкните → Учебное пособие по DIP (обработка цифровых изображений).
Обнаружение края
Давайте обсудим, как обнаружение краев помогает при обработке изображений.
Что такое обнаружение краев?
Обнаружение краев - это метод обработки изображений для определения границ объектов внутри изображений. Он работает, обнаруживая скачки яркости. Обнаружение краев используется для сегментации изображения и извлечения данных в таких областях, как обработка изображений, компьютерное зрение и машинное зрение.
Наиболее часто используемые алгоритмы обнаружения кромок включают:
- Sobel
- Canny
- Prewitt
- Roberts
- Методы нечеткой логики
Рассмотрим следующий пример.
import scipy.ndimage as nd
import numpy as np
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
import matplotlib.pyplot as plt
plt.imshow(im)
plt.show()Вышеупомянутая программа сгенерирует следующий вывод.

Изображение выглядит как квадратный блок цветов. Теперь мы обнаружим края этих цветных блоков. Здесь ndimage предоставляет функцию под названиемSobelпровести эту операцию. Принимая во внимание, что NumPy предоставляетHypot функция для объединения двух результирующих матриц в одну.
Рассмотрим следующий пример.
import scipy.ndimage as nd
import matplotlib.pyplot as plt
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
sx = ndimage.sobel(im, axis = 0, mode = 'constant')
sy = ndimage.sobel(im, axis = 1, mode = 'constant')
sob = np.hypot(sx, sy)
plt.imshow(sob)
plt.show()Вышеупомянутая программа сгенерирует следующий вывод.
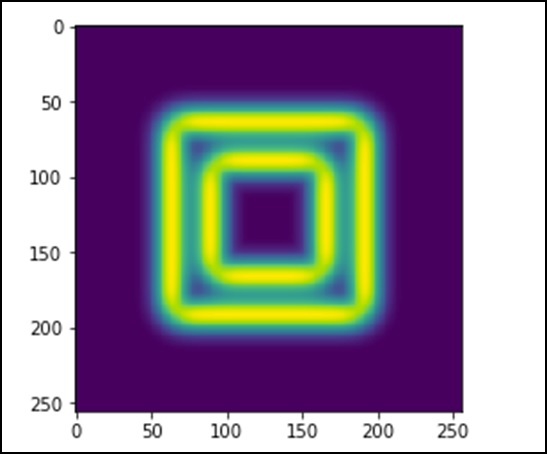
В scipy.optimize packageпредоставляет несколько часто используемых алгоритмов оптимизации. Этот модуль содержит следующие аспекты -
Неограниченная и ограниченная минимизация многомерных скалярных функций (минимизация ()) с использованием различных алгоритмов (например, BFGS, симплекс Нелдера-Мида, сопряженный градиент Ньютона, COBYLA или SLSQP)
Процедуры глобальной (грубой силы) оптимизации (например, anneal (), poolhopping ())
Алгоритмы минимизации наименьших квадратов (leastsq ()) и аппроксимации кривой (curve_fit ())
Минимизаторы скалярных одномерных функций (minim_scalar ()) и средства поиска корня (newton ())
Решатели многомерных систем уравнений (root ()) с использованием различных алгоритмов (например, гибридных методов Пауэлла, Левенберга-Марквардта или крупномасштабных методов, таких как Ньютон-Крылов)
Неограниченная и ограниченная минимизация многомерных скалярных функций
В minimize() function предоставляет общий интерфейс к алгоритмам неограниченной и ограниченной минимизации для многомерных скалярных функций в scipy.optimize. Чтобы продемонстрировать функцию минимизации, рассмотрим задачу минимизации функции Розенброка переменных NN -
$$f(x) = \sum_{i = 1}^{N-1} \:100(x_i - x_{i-1}^{2})$$
Минимальное значение этой функции равно 0, что достигается при xi = 1.
Симплексный алгоритм Нелдера – Мида
В следующем примере процедура минимизации () используется с Nelder-Mead simplex algorithm (method = 'Nelder-Mead')(выбирается с помощью параметра метода). Рассмотрим следующий пример.
import numpy as np
from scipy.optimize import minimize
def rosen(x):
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='nelder-mead')
print(res.x)Вышеупомянутая программа сгенерирует следующий вывод.
[7.93700741e+54 -5.41692163e+53 6.28769150e+53 1.38050484e+55 -4.14751333e+54]Симплексный алгоритм, вероятно, является самым простым способом минимизировать довольно хорошо работающую функцию. Он требует только оценки функций и является хорошим выбором для простых задач минимизации. Однако, поскольку он не использует никаких оценок градиента, поиск минимума может занять больше времени.
Другой алгоритм оптимизации, которому для нахождения минимума нужны только вызовы функций, - это Powell‘s method, который доступен путем установки method = 'powell' в функции minim ().
Наименьших квадратов
Решите нелинейную задачу наименьших квадратов с оценками переменных. Учитывая невязки f (x) (m-мерная вещественная функция n вещественных переменных) и функция потерь rho (s) (скалярная функция), функция minimum_squares находит локальный минимум функции стоимости F (x). Рассмотрим следующий пример.
В этом примере мы находим минимум функции Розенброка без ограничений на независимые переменные.
#Rosenbrock Function
def fun_rosenbrock(x):
return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])
from scipy.optimize import least_squares
input = np.array([2, 2])
res = least_squares(fun_rosenbrock, input)
print resОбратите внимание, что мы предоставляем только вектор остатков. Алгоритм строит функцию стоимости как сумму квадратов остатков, которая дает функцию Розенброка. Точный минимум находится при x = [1.0,1.0].
Вышеупомянутая программа сгенерирует следующий вывод.
active_mask: array([ 0., 0.])
cost: 9.8669242910846867e-30
fun: array([ 4.44089210e-15, 1.11022302e-16])
grad: array([ -8.89288649e-14, 4.44089210e-14])
jac: array([[-20.00000015,10.],[ -1.,0.]])
message: '`gtol` termination condition is satisfied.'
nfev: 3
njev: 3
optimality: 8.8928864934219529e-14
status: 1
success: True
x: array([ 1., 1.])Поиск корня
Давайте разберемся, как поиск корней помогает в SciPy.
Скалярные функции
Если у вас есть уравнение с одной переменной, есть четыре различных алгоритма поиска корня, которые можно попробовать. Для каждого из этих алгоритмов требуются конечные точки интервала, в котором ожидается корень (поскольку функция меняет знаки). В общем,brentq - лучший выбор, но другие методы могут быть полезны в определенных обстоятельствах или в академических целях.
Решение с фиксированной точкой
Проблема, тесно связанная с нахождением нулей функции, - это проблема нахождения неподвижной точки функции. Фиксированная точка функции - это точка, в которой оценка функции возвращает точку: g (x) = x. Ясно, что неподвижная точкаggявляется корнем f (x) = g (x) −x. Эквивалентно кореньffфиксированная_точка функции g (x) = f (x) + x. Подпрограмма fixed_point предоставляет простой итерационный метод с использованиемAitkens sequence acceleration оценить неподвижную точку gg, если задана отправная точка.
Наборы уравнений
Нахождение корня системы нелинейных уравнений может быть достигнуто с помощью root() function. Доступно несколько методов, среди которыхhybr (по умолчанию) и lm соответственно используют hybrid method of Powell и Levenberg-Marquardt method из MINPACK.
В следующем примере рассматривается трансцендентное уравнение с одной переменной.
x2 + 2cos(x) = 0
Корень которого можно найти следующим образом -
import numpy as np
from scipy.optimize import root
def func(x):
return x*2 + 2 * np.cos(x)
sol = root(func, 0.3)
print solВышеупомянутая программа сгенерирует следующий вывод.
fjac: array([[-1.]])
fun: array([ 2.22044605e-16])
message: 'The solution converged.'
nfev: 10
qtf: array([ -2.77644574e-12])
r: array([-3.34722409])
status: 1
success: True
x: array([-0.73908513])Все статистические функции находятся в подпакете scipy.stats и довольно полный список этих функций можно получить, используя info(stats)функция. Список доступных случайных величин также можно получить изdocstringдля подпакета статистики. Этот модуль содержит большое количество распределений вероятностей, а также растущую библиотеку статистических функций.
Каждое одномерное распределение имеет свой собственный подкласс, как описано в следующей таблице:
| Sr. No. | Класс и описание |
|---|---|
| 1 | rv_continuous Общий непрерывный класс случайных величин, предназначенный для создания подклассов |
| 2 | rv_discrete Общий класс дискретных случайных величин, предназначенный для создания подклассов |
| 3 | rv_histogram Создает распределение, заданное гистограммой |
Нормальная непрерывная случайная переменная
Распределение вероятностей, в котором случайная величина X может принимать любое значение, является непрерывной случайной величиной. Ключевое слово location (loc) определяет среднее значение. Ключевое слово scale (масштаб) определяет стандартное отклонение.
Как пример rv_continuous класс, norm объект наследует от него набор универсальных методов и дополняет их деталями, специфичными для этого конкретного распределения.
Чтобы вычислить CDF в нескольких точках, мы можем передать список или массив NumPy. Рассмотрим следующий пример.
from scipy.stats import norm
import numpy as np
print norm.cdf(np.array([1,-1., 0, 1, 3, 4, -2, 6]))Вышеупомянутая программа сгенерирует следующий вывод.
array([ 0.84134475, 0.15865525, 0.5 , 0.84134475, 0.9986501 ,
0.99996833, 0.02275013, 1. ])Чтобы найти медиану распределения, мы можем использовать функцию процентной точки (PPF), которая является обратной по отношению к CDF. Давайте разберемся, используя следующий пример.
from scipy.stats import norm
print norm.ppf(0.5)Вышеупомянутая программа сгенерирует следующий вывод.
0.0Чтобы сгенерировать последовательность случайных значений, мы должны использовать аргумент ключевого слова size, который показан в следующем примере.
from scipy.stats import norm
print norm.rvs(size = 5)Вышеупомянутая программа сгенерирует следующий вывод.
array([ 0.20929928, -1.91049255, 0.41264672, -0.7135557 , -0.03833048])Приведенный выше вывод не воспроизводится. Чтобы сгенерировать те же случайные числа, используйте функцию начального числа.
Равномерное распределение
Равномерное распределение может быть создано с помощью функции uniform. Рассмотрим следующий пример.
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)Вышеупомянутая программа сгенерирует следующий вывод.
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])Построить дискретное распределение
Сгенерируем случайную выборку и сравним наблюдаемые частоты с вероятностями.
Биномиальное распределение
Как пример rv_discrete class, то binom objectнаследует от него набор общих методов и дополняет их деталями, специфичными для этого конкретного дистрибутива. Рассмотрим следующий пример.
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)Вышеупомянутая программа сгенерирует следующий вывод.
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])Описательная статистика
Базовая статистика, такая как Min, Max, Mean и Variance, принимает массив NumPy в качестве входных данных и возвращает соответствующие результаты. Несколько основных статистических функций, доступных вscipy.stats package описаны в следующей таблице.
| Sr. No. | Описание функции |
|---|---|
| 1 | describe() Вычисляет несколько описательных статистик переданного массива |
| 2 | gmean() Вычисляет среднее геометрическое по указанной оси |
| 3 | hmean() Вычисляет среднее гармоническое по указанной оси. |
| 4 | kurtosis() Вычисляет эксцесс |
| 5 | mode() Возвращает модальное значение |
| 6 | skew() Проверяет асимметрию данных |
| 7 | f_oneway() Выполняет односторонний дисперсионный анализ |
| 8 | iqr() Вычисляет межквартильный диапазон данных по указанной оси |
| 9 | zscore() Вычисляет z-балл каждого значения в выборке относительно среднего значения выборки и стандартного отклонения. |
| 10 | sem() Вычисляет стандартную ошибку среднего (или стандартную ошибку измерения) значений во входном массиве. |
Некоторые из этих функций имеют аналогичную версию в scipy.stats.mstats, которые работают с маскированными массивами. Давайте разберемся в этом на примере, приведенном ниже.
from scipy import stats
import numpy as np
x = np.array([1,2,3,4,5,6,7,8,9])
print x.max(),x.min(),x.mean(),x.var()Вышеупомянутая программа сгенерирует следующий вывод.
(9, 1, 5.0, 6.666666666666667)Т-тест
Давайте разберемся, чем полезен T-тест в SciPy.
ttest_1samp
Вычисляет T-тест для среднего значения ОДНОЙ группы баллов. Это двусторонний тест для нулевой гипотезы о том, что ожидаемое значение (среднее) выборки независимых наблюдений 'a' равно заданному среднему значению генеральной совокупности,popmean. Рассмотрим следующий пример.
from scipy import stats
rvs = stats.norm.rvs(loc = 5, scale = 10, size = (50,2))
print stats.ttest_1samp(rvs,5.0)Вышеупомянутая программа сгенерирует следующий вывод.
Ttest_1sampResult(statistic = array([-1.40184894, 2.70158009]),
pvalue = array([ 0.16726344, 0.00945234]))Сравнение двух образцов
В следующих примерах представлены две выборки, которые могут происходить как из одного, так и из разных распределений, и мы хотим проверить, имеют ли эти образцы одинаковые статистические свойства.
ttest_ind- Вычисляет Т-критерий для средних значений двух независимых выборок оценок. Это двусторонняя проверка нулевой гипотезы о том, что две независимые выборки имеют одинаковые средние (ожидаемые) значения. Этот тест предполагает, что по умолчанию совокупности имеют идентичные дисперсии.
Мы можем использовать этот тест, если наблюдаем две независимые выборки из одной или разной совокупности. Рассмотрим следующий пример.
from scipy import stats
rvs1 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
rvs2 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
print stats.ttest_ind(rvs1,rvs2)Вышеупомянутая программа сгенерирует следующий вывод.
Ttest_indResult(statistic = -0.67406312233650278, pvalue = 0.50042727502272966)Вы можете протестировать то же самое с новым массивом той же длины, но с другим средним значением. Используйте другое значение вloc и проверить то же самое.
CSGraph означает Compressed Sparse Graph, который фокусируется на алгоритмах быстрых графов, основанных на представлениях разреженных матриц.
Графические представления
Для начала давайте разберемся, что такое разреженный граф и как он помогает в представлениях графов.
Что такое разреженный граф?
Граф - это просто набор узлов, между которыми есть связи. Графики могут представлять практически что угодно - связи в социальных сетях, где каждый узел - это человек и связан со знакомыми; изображения, где каждый узел является пикселем и связан с соседними пикселями; точки в распределении большой размерности, где каждый узел связан со своими ближайшими соседями; и практически все, что вы можете вообразить.
Один очень эффективный способ представления данных графа - это разреженная матрица: назовем ее G. Матрица G имеет размер N x N, а G [i, j] дает значение связи между узлом 'i' и узлом 'j'. Разреженный граф содержит в основном нули, то есть большинство узлов имеют только несколько соединений. Это свойство оказывается верным в большинстве интересных случаев.
Создание подмодуля разреженного графа было мотивировано несколькими алгоритмами, используемыми в scikit-learn, которые включали следующее:
Isomap - Алгоритм обучения многообразию, который требует нахождения кратчайших путей в графе.
Hierarchical clustering - Алгоритм кластеризации на основе минимального остовного дерева.
Spectral Decomposition - Алгоритм проекции, основанный на лапласианах разреженных графов.
В качестве конкретного примера представьте, что мы хотели бы представить следующий неориентированный граф -
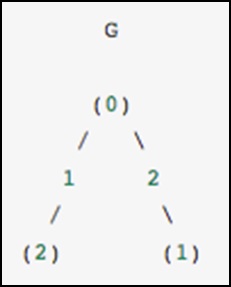
Этот граф имеет три узла, где узлы 0 и 1 соединены ребром веса 2, а узлы 0 и 2 соединены ребром веса 1. Мы можем построить плотные, замаскированные и разреженные представления, как показано в следующем примере. , имея в виду, что неориентированный граф представлен симметричной матрицей.
G_dense = np.array([ [0, 2, 1],
[2, 0, 0],
[1, 0, 0] ])
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix
G_sparse = csr_matrix(G_dense)
print G_sparse.dataВышеупомянутая программа сгенерирует следующий вывод.
array([2, 1, 2, 1])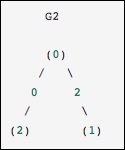
Это идентично предыдущему графу, за исключением того, что узлы 0 и 2 соединены ребром с нулевым весом. В этом случае плотное представление выше приводит к неоднозначности - как можно представить не ребра, если ноль является значимым значением. В этом случае для устранения неоднозначности необходимо использовать либо замаскированное, либо разреженное представление.
Рассмотрим следующий пример.
from scipy.sparse.csgraph import csgraph_from_dense
G2_data = np.array
([
[np.inf, 2, 0 ],
[2, np.inf, np.inf],
[0, np.inf, np.inf]
])
G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)
print G2_sparse.dataВышеупомянутая программа сгенерирует следующий вывод.
array([ 2., 0., 2., 0.])Словарные лестницы с использованием разреженных графов
Лестницы слов - это игра, изобретенная Льюисом Кэрроллом, в которой слова связываются путем изменения одной буквы на каждом шаге. Например -
APE → APT → AIT → BIT → BIG → BAG → MAG → MAN
Здесь мы перешли от «APE» к «MAN» за семь шагов, каждый раз меняя одну букву. Вопрос в том, можем ли мы найти более короткий путь между этими словами, используя то же правило? Эта проблема естественно выражается как проблема разреженного графа. Узлы будут соответствовать отдельным словам, и мы создадим связи между словами, которые отличаются максимум - одной буквой.
Получение списка слов
Сначала, конечно, мы должны получить список допустимых слов. Я использую Mac, и у Mac есть словарь слов в месте, указанном в следующем блоке кода. Если вы используете другую архитектуру, вам, возможно, придется немного поискать, чтобы найти свой системный словарь.
wordlist = open('/usr/share/dict/words').read().split()
print len(wordlist)Вышеупомянутая программа сгенерирует следующий вывод.
235886Теперь мы хотим взглянуть на слова длины 3, поэтому давайте выберем только те слова правильной длины. Мы также исключим слова, которые начинаются с верхнего регистра (имена собственные) или содержат не буквенно-цифровые символы, такие как апострофы и дефисы. Наконец, мы убедимся, что все написано в нижнем регистре, для сравнения позже.
word_list = [word for word in word_list if len(word) == 3]
word_list = [word for word in word_list if word[0].islower()]
word_list = [word for word in word_list if word.isalpha()]
word_list = map(str.lower, word_list)
print len(word_list)Вышеупомянутая программа сгенерирует следующий вывод.
1135Теперь у нас есть список из 1135 допустимых трехбуквенных слов (точное число может меняться в зависимости от конкретного используемого списка). Каждое из этих слов станет узлом в нашем графе, и мы создадим ребра, соединяющие узлы, связанные с каждой парой слов, которая отличается только одной буквой.
import numpy as np
word_list = np.asarray(word_list)
word_list.dtype
word_list.sort()
word_bytes = np.ndarray((word_list.size, word_list.itemsize),
dtype = 'int8',
buffer = word_list.data)
print word_bytes.shapeВышеупомянутая программа сгенерирует следующий вывод.
(1135, 3)Мы будем использовать расстояние Хэмминга между каждой точкой, чтобы определить, какие пары слов связаны. Расстояние Хэмминга измеряет долю записей между двумя векторами, которые различаются: любые два слова с расстоянием Хэмминга, равным 1 / N1 / N, где NN - количество букв, которые связаны в словарной лестнице.
from scipy.spatial.distance import pdist, squareform
from scipy.sparse import csr_matrix
hamming_dist = pdist(word_bytes, metric = 'hamming')
graph = csr_matrix(squareform(hamming_dist < 1.5 / word_list.itemsize))При сравнении расстояний мы не используем равенство, потому что это может быть нестабильным для значений с плавающей запятой. Неравенство дает желаемый результат до тех пор, пока никакие две записи списка слов не совпадают. Теперь, когда наш граф настроен, мы будем использовать поиск по кратчайшему пути, чтобы найти путь между любыми двумя словами в графе.
i1 = word_list.searchsorted('ape')
i2 = word_list.searchsorted('man')
print word_list[i1],word_list[i2]Вышеупомянутая программа сгенерирует следующий вывод.
ape, manНам нужно проверить, что они совпадают, потому что, если слов нет в списке, на выходе будет ошибка. Теперь все, что нам нужно, - это найти кратчайший путь между этими двумя индексами в графе. Мы будем использоватьdijkstra’s алгоритм, потому что он позволяет нам найти путь только для одного узла.
from scipy.sparse.csgraph import dijkstra
distances, predecessors = dijkstra(graph, indices = i1, return_predecessors = True)
print distances[i2]Вышеупомянутая программа сгенерирует следующий вывод.
5.0Таким образом, мы видим, что кратчайший путь между «обезьяной» и «человеком» состоит всего из пяти шагов. Мы можем использовать предшественников, возвращенных алгоритмом, для восстановления этого пути.
path = []
i = i2
while i != i1:
path.append(word_list[i])
i = predecessors[i]
path.append(word_list[i1])
print path[::-1]i2]Вышеупомянутая программа сгенерирует следующий вывод.
['ape', 'ope', 'opt', 'oat', 'mat', 'man']В scipy.spatial package может вычислять триангуляции, диаграммы Вороного и выпуклые оболочки набора точек, используя Qhull library. Кроме того, он содержитKDTree implementations для запросов точки ближайшего соседа и утилит для вычисления расстояния в различных показателях.
Триангуляции Делоне
Давайте разберемся, что такое триангуляции Делоне и как они используются в SciPy.
Что такое триангуляции Делоне?
В математике и вычислительной геометрии триангуляция Делоне для заданного множества P дискретных точек на плоскости представляет собой триангуляцию DT(P) так что нет смысла в P находится внутри описанной окружности любого треугольника в DT (P).
Мы можем вычислить то же самое через SciPy. Рассмотрим следующий пример.
from scipy.spatial import Delaunay
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()Вышеупомянутая программа сгенерирует следующий вывод.

Копланарные точки
Давайте разберемся, что такое Coplanar Points и как они используются в SciPy.
Что такое копланарные точки?
Копланарные точки - это три или более точки, лежащие в одной плоскости. Напомним, что плоскость - это плоская поверхность, которая проходит без конца во всех направлениях. Обычно в учебниках математики он изображается в виде четырехгранной фигуры.
Давайте посмотрим, как мы можем найти это с помощью SciPy. Рассмотрим следующий пример.
from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanarВышеупомянутая программа сгенерирует следующий вывод.
array([[4, 0, 3]], dtype = int32)Это означает, что точка 4 находится рядом с треугольником 0 и вершиной 3, но не включена в триангуляцию.
Выпуклые корпуса
Давайте разберемся, что такое выпуклые оболочки и как они используются в SciPy.
Что такое выпуклая оболочка?
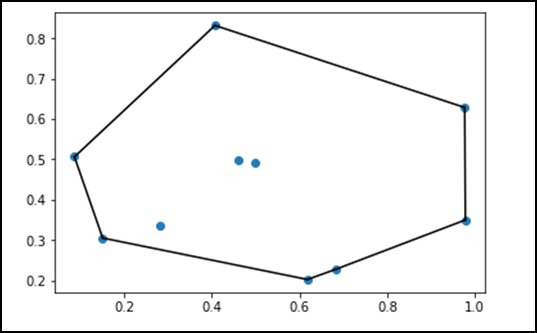
В математике convex hull или же convex envelope набора точек X на евклидовой плоскости или в евклидовом пространстве (или, в более общем смысле, в аффинном пространстве над вещественными числами) является наименьшим convex set который содержит X.
Давайте рассмотрим следующий пример, чтобы понять это подробно.
from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()Вышеупомянутая программа сгенерирует следующий вывод.
ODR означает Orthogonal Distance Regression, который используется в регрессионных исследованиях. Базовая линейная регрессия часто используется для оценки взаимосвязи между двумя переменными.y и x проведя линию наилучшего соответствия на графике.
Используемый для этого математический метод известен как Least Squares, и стремится минимизировать сумму квадратов ошибок для каждой точки. Ключевой вопрос здесь - как рассчитать ошибку (также известную как невязка) для каждой точки?
В стандартной линейной регрессии цель состоит в том, чтобы предсказать значение Y по значению X, поэтому разумно рассчитать ошибку в значениях Y (показано серыми линиями на следующем изображении). Однако иногда более разумно учитывать ошибку как по X, так и по Y (как показано пунктирными красными линиями на следующем изображении).
Например - когда вы знаете, что ваши измерения X неточны, или когда вы не хотите сосредотачиваться на ошибках одной переменной над другой.
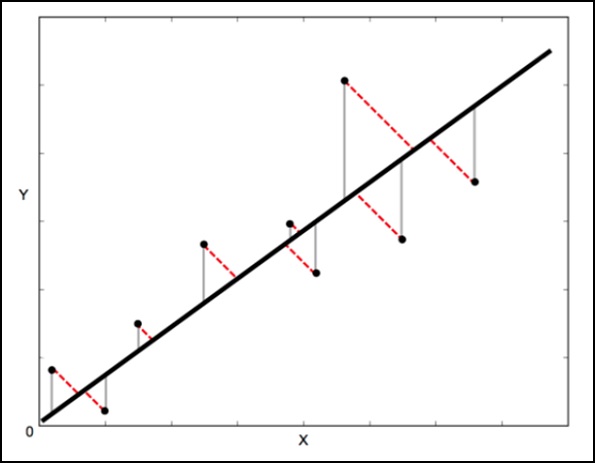
Ортогональная дистанционная регрессия (ODR) - это метод, который может это сделать (ортогональный в этом контексте означает перпендикулярный - поэтому он вычисляет ошибки перпендикулярно линии, а не просто «вертикально»).
scipy.odr Реализация для одномерной регрессии
В следующем примере демонстрируется реализация scipy.odr для одномерной регрессии.
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random
# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])
# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
m, c = p
return m*x + c
# Create a model for fitting.
linear_model = Model(linear_func)
# Create a RealData object using our initiated data from above.
data = RealData(x, y)
# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])
# Run the regression.
out = odr.run()
# Use the in-built pprint method to give us results.
out.pprint()Вышеупомянутая программа сгенерирует следующий вывод.
Beta: [ 5.51846098 -4.25744878]
Beta Std Error: [ 0.7786442 2.33126407]
Beta Covariance: [
[ 1.93150969 -4.82877433]
[ -4.82877433 17.31417201
]]
Residual Variance: 0.313892697582
Inverse Condition #: 0.146618499389
Reason(s) for Halting:
Sum of squares convergenceВ специальном пакете доступны универсальные функции, которые следуют за широковещательной рассылкой и автоматическим зацикливанием массива.
Давайте посмотрим на некоторые из наиболее часто используемых специальных функций -
- Кубическая корневая функция
- Экспоненциальная функция
- Экспоненциальная функция относительной ошибки
- Экспоненциальная функция лог-суммы
- Функция Ламберта
- Функция перестановок и комбинаций
- Гамма-функция
Давайте теперь вкратце разберемся с каждой из этих функций.
Кубическая корневая функция
Синтаксис этой кубической корневой функции - scipy.special.cbrt (x). Это приведет к поэлементному извлечению кубического корня изx.
Рассмотрим следующий пример.
from scipy.special import cbrt
res = cbrt([10, 9, 0.1254, 234])
print resВышеупомянутая программа сгенерирует следующий вывод.
[ 2.15443469 2.08008382 0.50053277 6.16224015]Экспоненциальная функция
Синтаксис экспоненциальной функции - scipy.special.exp10 (x). Это будет вычислять 10 ** x поэлементно.
Рассмотрим следующий пример.
from scipy.special import exp10
res = exp10([2, 9])
print resВышеупомянутая программа сгенерирует следующий вывод.
[1.00000000e+02 1.00000000e+09]Экспоненциальная функция относительной ошибки
Синтаксис этой функции - scipy.special.exprel (x). Он генерирует экспоненту относительной ошибки (exp (x) - 1) / x.
когда xблизко к нулю, exp (x) близко к 1, поэтому численное вычисление exp (x) - 1 может страдать от катастрофической потери точности. Затем используется exprel (x), чтобы избежать потери точности, которая происходит, когдаx близок к нулю.
Рассмотрим следующий пример.
from scipy.special import exprel
res = exprel([-0.25, -0.1, 0, 0.1, 0.25])
print resВышеупомянутая программа сгенерирует следующий вывод.
[0.88479687 0.95162582 1. 1.05170918 1.13610167]Экспоненциальная функция лог-суммы
Синтаксис этой функции - scipy.special.logsumexp (x). Это помогает вычислить логарифм суммы экспонент входных элементов.
Рассмотрим следующий пример.
from scipy.special import logsumexp
import numpy as np
a = np.arange(10)
res = logsumexp(a)
print resВышеупомянутая программа сгенерирует следующий вывод.
9.45862974443Функция Ламберта
Синтаксис этой функции - scipy.special.lambertw (x). Ее также называют W-функцией Ламберта. Функция Ламберта W W (z) определяется как функция, обратная к w * exp (w). Другими словами, значение W (z) таково, что z = W (z) * exp (W (z)) для любого комплексного числа z.
Функция Ламберта W является многозначной функцией с бесконечным числом ветвей. Каждая ветвь дает отдельное решение уравнения z = w exp (w). Здесь ветви пронумерованы целым числом k.
Рассмотрим следующий пример. Здесь функция Ламберта W является обратной к w exp (w).
from scipy.special import lambertw
w = lambertw(1)
print w
print w * np.exp(w)Вышеупомянутая программа сгенерирует следующий вывод.
(0.56714329041+0j)
(1+0j)Перестановки и комбинации
Давайте обсудим перестановки и комбинации отдельно для их четкого понимания.
Combinations- Синтаксис функции комбинаций - scipy.special.comb (N, k). Давайте рассмотрим следующий пример -
from scipy.special import comb
res = comb(10, 3, exact = False,repetition=True)
print resВышеупомянутая программа сгенерирует следующий вывод.
220.0Note- Аргументы массива принимаются только для случая точного = Ложь. Если k> N, N <0 или k <0, то возвращается 0.
Permutations- Синтаксис функции комбинаций - scipy.special.perm (N, k). Перестановки N вещей, взятых k за раз, то есть k-перестановки N. Это также известно как «частичные перестановки».
Рассмотрим следующий пример.
from scipy.special import perm
res = perm(10, 3, exact = True)
print resВышеупомянутая программа сгенерирует следующий вывод.
720Гамма-функция
Гамма-функцию часто называют обобщенным факториалом, поскольку z * gamma (z) = gamma (z + 1) и gamma (n + 1) = n !, для натурального числа «n».
Синтаксис функции комбинаций - scipy.special.gamma (x). Перестановки N вещей, взятых k за раз, то есть k-перестановки N. Это также известно как «частичные перестановки».
Синтаксис функции комбинаций - scipy.special.gamma (x). Перестановки N вещей, взятых k за раз, то есть k-перестановки N. Это также известно как «частичные перестановки».
from scipy.special import gamma
res = gamma([0, 0.5, 1, 5])
print resВышеупомянутая программа сгенерирует следующий вывод.
[inf 1.77245385 1. 24.]