SciPy - Пространственный
В scipy.spatial package может вычислять триангуляции, диаграммы Вороного и выпуклые оболочки набора точек, используя Qhull library. Кроме того, он содержитKDTree implementations для запросов точки ближайшего соседа и утилит для вычисления расстояния в различных показателях.
Триангуляции Делоне
Давайте разберемся, что такое триангуляции Делоне и как они используются в SciPy.
Что такое триангуляции Делоне?
В математике и вычислительной геометрии триангуляция Делоне для заданного набора P дискретных точек на плоскости представляет собой триангуляцию DT(P) так что нет смысла в P находится внутри описанной окружности любого треугольника в DT (P).
Мы можем вычислить то же самое через SciPy. Рассмотрим следующий пример.
from scipy.spatial import Delaunay
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()Вышеупомянутая программа выдаст следующий результат.

Копланарные точки
Давайте разберемся, что такое Coplanar Points и как они используются в SciPy.
Что такое копланарные точки?
Копланарные точки - это три или более точки, лежащие в одной плоскости. Напомним, что плоскость - это плоская поверхность, которая проходит без конца во всех направлениях. Обычно в учебниках по математике он изображается в виде четырехгранной фигуры.
Давайте посмотрим, как мы можем найти это с помощью SciPy. Рассмотрим следующий пример.
from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanarВышеупомянутая программа выдаст следующий результат.
array([[4, 0, 3]], dtype = int32)Это означает, что точка 4 находится около треугольника 0 и вершины 3, но не включена в триангуляцию.
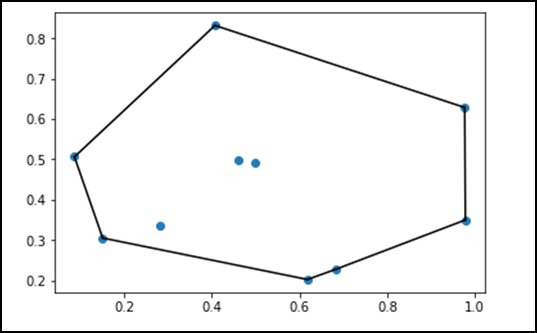
Выпуклые корпуса
Давайте разберемся, что такое выпуклые оболочки и как они используются в SciPy.
Что такое выпуклая оболочка?
В математике convex hull или же convex envelope набора точек X на евклидовой плоскости или в евклидовом пространстве (или, в более общем смысле, в аффинном пространстве над вещественными числами) является наименьшим convex set который содержит X.
Давайте рассмотрим следующий пример, чтобы понять это подробно.
from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()Вышеупомянутая программа выдаст следующий результат.