SymPy - Краткое руководство

SymPy - это библиотека Python для выполнения символьных вычислений. Этоcomputer algebra system(CAS), который можно использовать как отдельное приложение или как библиотеку для других приложений. Его прямая трансляция также доступна наhttps://live.sympy.org/. Поскольку это чистая библиотека Python, ее можно использовать как в интерактивном режиме, так и в качестве программного приложения. SymPy теперь стала популярной символической библиотекой для научной экосистемы Python.

SymPy имеет широкий спектр функций, применимых в области базовой символьной арифметики, исчисления, алгебры, дискретной математики, квантовой физики и т. Д. SymPy может форматировать результаты в различных форматах, включая LaTeX, MathML и т. Д. SymPy распространяется под Новая лицензия BSD. Команда разработчиков во главе сOndřej Čertík и Aaron Meurer опубликовал первую версию SymPy в 2007 году. Текущая версия - 1.5.1.

Некоторые из областей применения SymPy:

• Polynomials
• Calculus
• Дискретная математика
• Matrices
• Geometry
• Plotting
• Physics
• Statistics
• Combinatorics

SymPy имеет одну важную предварительную библиотеку с именем mpmath. Это библиотека Python для реальной и сложной арифметики с плавающей запятой с произвольной точностью. Однако установщик пакетов Python PIP устанавливает его автоматически при установке SymPy следующим образом:

pip install sympy

В других дистрибутивах Python, таких как Anaconda, Enthought Canopy и т. Д., Может быть уже включен SymPy. Чтобы проверить, вы можете ввести следующее в командной строке Python -

>>> import sympy
>>> sympy.__version__

И вы получите следующий результат как текущую версию sympy -

'1.5.1'

Исходный код пакета SymPy доступен по адресу https://github.com/sympy/sympy.

Символьные вычисления относятся к разработке алгоритмов для управления математическими выражениями и другими математическими объектами. Символьные вычисления объединяют математику с информатикой для решения математических выражений с использованием математических символов. Система компьютерной алгебры (CAS), такая как SymPy, точно (а не приблизительно) вычисляет алгебраические выражения, используя те же символы, которые используются в традиционном ручном методе. Например, мы вычисляем квадратный корень из числа, используя математический модуль Python, как показано ниже -

>>> import math 
>>> print (math.sqrt(25), math.sqrt(7))

Вывод для приведенного выше фрагмента кода следующий:

5.0 2.6457513110645907

Как видите, квадратный корень из 7 рассчитывается приблизительно. Но в SymPy квадратные корни чисел, которые не являются точными квадратами, по умолчанию не вычисляются, как указано ниже -

>>> import sympy 
>>> print (sympy.sqrt(7))

Вывод для приведенного выше фрагмента кода следующий:

sqrt(7)

Можно упростить и показать результат выражения символически с помощью фрагмента кода ниже -

>>> import math
>>> print (math.sqrt(12))

Вывод для приведенного выше фрагмента кода следующий:

3.4641016151377544

Вам нужно использовать приведенный ниже фрагмент кода, чтобы выполнить то же самое с помощью sympy -

##sympy output 
>>> print (sympy.sqrt(12))

И результат для этого следующий -

2*sqrt(3)

Код SymPy при запуске в блокноте Jupyter использует библиотеку MathJax для отображения математических символов в форме LatEx. Это показано во фрагменте кода ниже -

>>> from sympy import * 
>>> x=Symbol ('x') 
>>> expr = integrate(x**x, x) 
>>> expr

При выполнении вышеуказанной команды в оболочке python будет сгенерирован следующий вывод:

Integral(x**x, x)

Что эквивалентно

$\int \mathrm{x}^{x}\,\mathrm{d}x$

Квадратный корень из неполного квадрата может быть представлен латексом следующим образом с использованием традиционного символа -

>>> from sympy import * 
>>> x=7 
>>> sqrt(x)

Вывод для приведенного выше фрагмента кода следующий:

$\sqrt7$

Система символьных вычислений, такая как SymPy, выполняет все виды вычислений (например, производные, интегралы и пределы, решает уравнения, работает с матрицами) символически. В пакете SymPy есть различные модули, которые поддерживают построение графиков, печать (например, LATEX), физику, статистику, комбинаторику, теорию чисел, геометрию, логику и т. Д.

Основной модуль в пакете SymPy содержит класс Number, который представляет атомные числа. Этот класс имеет два подкласса: класс Float и Rational. Класс Rational расширен классом Integer.

Класс Float представляет собой число с плавающей запятой произвольной точности.

>>> from sympy import Float 
>>> Float(6.32)

Вывод для приведенного выше фрагмента кода следующий:

6.32

SymPy может преобразовывать целое число или строку в число с плавающей запятой.

>>> Float(10)

10.0

Float('1.33E5')# scientific notation

133000.0

При преобразовании в число с плавающей запятой также можно указать количество цифр для точности, как указано ниже -

>>> Float(1.33333,2)

Вывод для приведенного выше фрагмента кода следующий:

1.3

Представление числа (p / q) представлено как объект класса Rational, где q - ненулевое число.

>>> Rational(3/4)

Вывод для приведенного выше фрагмента кода следующий:

$\frac{3}{4}$

Если число с плавающей запятой передается конструктору Rational (), он возвращает базовое значение своего двоичного представления.

>>> Rational(0.2)

Вывод для приведенного выше фрагмента кода следующий:

$\frac{3602879701896397}{18014398509481984}$

Для упрощения представления укажите ограничение знаменателя.

>>> Rational(0.2).limit_denominator(100)

Вывод для приведенного выше фрагмента кода следующий:

$\frac{1}{5}$

Когда строка передается конструктору Rational (), возвращается рациональное число произвольной точности.

>>> Rational("3.65")

Вывод для приведенного выше фрагмента кода следующий:

$\frac{73}{20}$

Рациональный объект также может быть получен, если переданы два числовых аргумента. Части числителя и знаменателя доступны как свойства.

>>> a=Rational(3,5) 
>>> print (a) 
>>> print ("numerator:{}, denominator:{}".format(a.p, a.q))

Вывод для приведенного выше фрагмента кода следующий:

3/5

numerator:3, denominator:5

>>> a

Вывод для приведенного выше фрагмента кода следующий:

$\frac{3}{5}$

Целочисленный класс в SymPy представляет собой целое число любого размера. Конструктор может принимать число с плавающей запятой или рациональное число, но дробная часть отбрасывается.

>>> Integer(10)

Вывод для приведенного выше фрагмента кода следующий:

10

>>> Integer(3.4)

Вывод для приведенного выше фрагмента кода следующий:

3

>>> Integer(2/7)

Вывод для приведенного выше фрагмента кода следующий:

0

SymPy имеет RealNumberкласс, который действует как псевдоним для Float. SymPy также определяет Zero и One как одноэлементные классы, доступные через S.Zero и S.One соответственно, как показано ниже -

>>> S.Zero

Результат выглядит следующим образом -

0

>>> S.One

Результат выглядит следующим образом -

1

Другими предопределенными объектами числа Singleton являются Half, NaN, Infinity и ImaginaryUnit.

>>> from sympy import S 
>>> print (S.Half)

Результат выглядит следующим образом -

½

>>> print (S.NaN)

Результат выглядит следующим образом -

nan

Бесконечность доступна как объект символа oo или S.Infinity.

>>> from sympy import oo 
>>> oo

Вывод для приведенного выше фрагмента кода следующий:

$\infty$

>>> S.Infinity

Вывод для приведенного выше фрагмента кода следующий:

$\infty$

Номер ImaginaryUnit может быть импортирован как символ I или доступен как S.ImaginaryUnit и представляет собой квадратный корень из -1.

>>> from sympy import I 
>>> I

Когда вы выполняете приведенный выше фрагмент кода, вы получаете следующий результат:

i

>>> S.ImaginaryUnit

Вывод приведенного выше фрагмента выглядит следующим образом:

i

>>> from sympy import sqrt 
>>> i=sqrt(-1) 
>>> i*i

Когда вы выполняете приведенный выше фрагмент кода, вы получаете следующий результат:

-1

Symbolэто самый важный класс в библиотеке symPy. Как упоминалось ранее, символьные вычисления выполняются с помощью символов. Переменные SymPy являются объектами класса Symbols.

Аргументом функции Symbol () является строка, содержащая символ, который можно присвоить переменной.

>>> from sympy import Symbol 
>>> x=Symbol('x') 
>>> y=Symbol('y') 
>>> expr=x**2+y**2 
>>> expr

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x^2 + y^2$

Символ может состоять из более чем одного алфавита.

>>> s=Symbol('side') 
>>> s**3

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$side^3$

SymPy также имеет Symbols()функция, которая может определять несколько символов одновременно. Строка содержит имена переменных, разделенных запятой или пробелом.

>>> from sympy import symbols 
>>> x,y,z=symbols("x,y,z")

В модуле abc SymPy все латинские и греческие алфавиты определены как символы. Следовательно, этот метод удобен вместо создания экземпляра объекта Symbol.

>>> from sympy.abc import x,y,z

Однако имена C, O, S, I, N, E и Qпредопределенные символы. Кроме того, символы с более чем одним алфавитом не определены в модуле abc, для которого вы должны использовать объект Symbol, как указано выше. Модуль abc определяет специальные имена, которые могут обнаруживать определения в пространстве имен SymPy по умолчанию. clash1 содержит одиночные буквы, а clash2 - многобуквенные символы конфликта

>>> from sympy.abc import _clash1, _clash2 
>>> _clash1

Вывод приведенного выше фрагмента выглядит следующим образом:

{'C': C, 'O': O, 'Q': Q, 'N': N, 'I': I, 'E': E, 'S': S}

>>> _clash2

Вывод приведенного выше фрагмента выглядит следующим образом:

{'beta': beta, 'zeta': zeta, 'gamma': gamma, 'pi': pi}

Индексированные символы могут быть определены с использованием синтаксиса, аналогичного функции range (). Диапазоны обозначаются двоеточием. Тип диапазона определяется символом справа от двоеточия. Если itr - цифра, все смежные цифры слева принимаются в качестве неотрицательного начального значения. Все смежные цифры справа считаются на 1 больше конечного значения.

>>> from sympy import symbols 
>>> symbols('a:5')

Вывод приведенного выше фрагмента выглядит следующим образом:

(a0, a1, a2, a3, a4)

>>> symbols('mark(1:4)')

Вывод приведенного выше фрагмента выглядит следующим образом:

(mark1, mark2, mark3)

Одна из самых простых операций, выполняемых с математическим выражением, - это подстановка. Функция subs () в SymPy заменяет все вхождения первого параметра вторым.

>>> from sympy.abc import x,a 
>>> expr=sin(x)*sin(x)+cos(x)*cos(x) 
>>> expr

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\sin^2(x)+\cos^2(x)$

>>> expr.subs(x,a)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\sin^2(a)+\cos^2(a)$

Эта функция полезна, если мы хотим оценить определенное выражение. Например, мы хотим вычислить значения следующего выражения, заменив a на 5.

>>> expr=a*a+2*a+5 
>>> expr

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$a^2 + 2a + 5$

expr.subs(a,5)

Приведенный выше фрагмент кода дает следующий результат -

40

>>> from sympy.abc import x 
>>> from sympy import sin, pi 
>>> expr=sin(x) 
>>> expr1=expr.subs(x,pi) 
>>> expr1

Приведенный выше фрагмент кода дает следующий результат -

0

Эта функция также используется для замены части выражения на другую часть выражения. В следующем примере b заменяется на a + b.

>>> from sympy.abc import a,b 
>>> expr=(a+b)**2 
>>> expr1=expr.subs(b,a+b) 
>>> expr1

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$(2a + b)^2$

Функция sympify () используется для преобразования любого произвольного выражения, чтобы его можно было использовать как выражение SymPy. Обычные объекты Python, такие как целочисленные объекты, конвертируются в SymPy. Целые числа и т. Д., Строки также преобразуются в выражения SymPy.

>>> expr="x**2+3*x+2" 
>>> expr1=sympify(expr) 
>>> expr1 
>>> expr1.subs(x,2)

Приведенный выше фрагмент кода дает следующий результат -

12

Любой объект Python можно преобразовать в объект SymPy. Однако, поскольку преобразование внутренне использует функцию eval (), не следует использовать несанкционированное выражение, иначе возникает SympifyError.

>>> sympify("x***2")
---------------------------------------------------------------------------

SympifyError: ошибка Sympify выражения "не удалось проанализировать" x *** 2 "из-за того, что возникло исключение.

Функция sympify () принимает следующие аргументы: * strict: по умолчанию False. Если установлено значение True, преобразуются только типы, для которых определено явное преобразование. В противном случае возникает SympifyError. * оценить: если установлено значение False, арифметические операции и операторы будут преобразованы в их эквиваленты в SymPy без оценки выражения.

>>> sympify("10/5+4/2")

Приведенный выше фрагмент кода дает следующий результат -

4

>>> sympify("10/5+4/2", evaluate=False)

Приведенный выше фрагмент кода дает следующий результат -

$\frac{10}{5}+\frac{4}{2}$

Эта функция оценивает данное числовое выражение с точностью до 100 цифр с плавающей запятой. Функция также принимает параметр subs как объект словаря числовых значений для символов. Рассмотрим следующее выражение

>>> from sympy.abc import r 
>>> expr=pi*r**2 
>>> expr

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\Pi{r^2}$

Чтобы оценить приведенное выше выражение с помощью функции evalf (), заменив r на 5

>>> expr.evalf(subs={r:5})

Приведенный выше фрагмент кода дает следующий результат -

78.5398163397448

По умолчанию точность с плавающей запятой составляет до 15 цифр, которые могут быть заменены любым числом до 100. Следующее выражение оценивается с точностью до 20 цифр.

>>> expr=a/b 
>>> expr.evalf(20, subs={a:100, b:3})

Приведенный выше фрагмент кода дает следующий результат -

33.333333333333333333

Функция lambdify переводит выражения SymPy в функции Python. Если выражение должно оцениваться в большом диапазоне значений, функция evalf () неэффективна. lambdify действует как лямбда-функция, за исключением того, что он преобразует имена SymPy в имена заданной числовой библиотеки, обычно NumPy. По умолчанию lambdify реализуется в стандартной математической библиотеке.

>>> expr=1/sin(x) 
>>> f=lambdify(x, expr) 
>>> f(3.14)

Приведенный выше фрагмент кода дает следующий результат -

627.8831939138764

Выражение может иметь более одной переменной. В этом случае первым аргументом функции lambdify () является список переменных, за которым следует выражение, которое нужно оценить.

>>> expr=a**2+b**2 
>>> f=lambdify([a,b],expr) 
>>> f(2,3)

Приведенный выше фрагмент кода дает следующий результат -

13

Однако, чтобы использовать библиотеку numpy в качестве числового бэкенда, мы должны определить то же самое в качестве аргумента для функции lambdify ().

>>> f=lambdify([a,b],expr, "numpy")

Мы используем два массива numpy для двух аргументов a и b в приведенной выше функции. Время выполнения значительно меньше в случае массивов numpy.

>>> import numpy 
>>> l1=numpy.arange(1,6) 
>>> l2=numpy.arange(6,11) 
>>> f(l1,l2)

Приведенный выше фрагмент кода дает следующий результат -

array([ 37, 53, 73, 97, 125], dtype=int32)

Булевы функции определены в sympy.basic.booleanarg module. Можно создавать логические выражения с помощью стандартных операторов Python & (And), | (Или), ~ (Не), а также с >> и <<. Логические выражения наследуются от класса Basic, определенного в основном модуле SymPy.

Функция BooleanTrue

Эта функция эквивалентна True, как в ядре Python. Он возвращает синглтон, который может быть получен S.true.

>>> from sympy import * 
>>> x=sympify(true) 
>>> x, S.true

Приведенный выше фрагмент кода дает следующий результат -

(Правда правда)

Функция BooleanFalse

Точно так же эта функция эквивалентна Boolean False в Python и может быть доступна с помощью S.false

>>> from sympy import * 
>>> x=sympify(false) 
>>> x, S.false

Приведенный выше фрагмент кода дает следующий результат -

(Ложь, Ложь)

И функция

Логическая функция И оценивает два своих аргумента и возвращает False, если любой из них имеет значение False. Функция эмулирует оператор &.

>>> from sympy import * 
>>> from sympy.logic.boolalg import And 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=True 
>>> And(x,y), x"&"y

Приведенный выше фрагмент кода дает следующий результат -

(Правда правда)

>>> y=False 
>>> And(x,y), x"&"y

Приведенный выше фрагмент кода дает следующий результат -

(Ложь, Ложь)

Или функция

Эта функция оценивает два логических аргумента и возвращает True, если любой из них имеет значение True. | Оператор удобно имитирует его поведение.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Or 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False 
>>> Or(x,y), x|y

Приведенный выше фрагмент кода дает следующий результат -

(Правда правда)

>>> x=False 
>>> y=False 
>>> Or(x,y), x|y

Приведенный выше фрагмент кода дает следующий результат -

(Ложь, Ложь)

Не работает

Функция Logical Not приводит к отрицанию логического аргумента. Он возвращает True, если его аргумент равен False, и возвращает False, если True. Оператор ~ выполняет операцию, аналогичную функции Not. Это показано в примере ниже -

>>> from sympy import * 
>>> from sympy.logic.boolalg import Or, And, Not 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False 
>>> Not(x), Not(y)

Приведенный выше фрагмент кода дает следующий результат -

(Ложь Правда)

>>> Not(And(x,y)), Not(Or(x,y))

Приведенный выше фрагмент кода дает следующий результат -

(Верно, неверно)

Функция Xor

Функция логического XOR (исключающее ИЛИ) возвращает True, если нечетное число аргументов равно True, а остальные - False, и возвращает False, если четное количество аргументов имеет значение True, а остальные - False. Аналогичную операцию выполняет оператор ^.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Xor 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False

>>> Xor(x,y), x^y

Приведенный выше фрагмент кода дает следующий результат -

(Правда правда)

>>> a,b,c,d,e=symbols('a b c d e') 
>>> a,b,c,d,e=(True, False, True, True, False) 
>>> Xor(a,b,c,d,e)

Приведенный выше фрагмент кода дает следующий результат -

Правда

В приведенном выше случае три аргумента (нечетное число) имеют значение True, поэтому Xor возвращает true. Однако, если количество аргументов True четное, это приводит к False, как показано ниже -

>>> a,b,c,d,e=(True, False, False, True, False) 
>>> Xor(a,b,c,d,e)

Приведенный выше фрагмент кода дает следующий результат -

Ложь

Функция Nand

Эта функция выполняет операцию логической И-НЕ. Он оценивает свои аргументы и возвращает True, если любой из них имеет значение False, и False, если все они истинны.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Nand 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Nand(a,b,c), Nand(a,c)

Приведенный выше фрагмент кода дает следующий результат -

(Верно, неверно)

Ни функции

Эта функция выполняет операцию логического ИЛИ-ИЛИ. Он оценивает свои аргументы и возвращает False, если какой-либо из них является True, и True, если все они ложны.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Nor 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Nor(a,b,c), Nor(a,c)

Приведенный выше фрагмент кода дает следующий результат -

(Ложь, Ложь)

Обратите внимание, что хотя SymPy предоставляет оператор ^ для Xor, ~ для Not, | для функций Or и & для And для удобства, их обычное использование в Python - побитовые операторы. Следовательно, если операнды являются целыми числами, результаты будут другими.

Эквивалентная функция

Эта функция возвращает отношение эквивалентности. Эквивалент (A, B) равен True тогда и только тогда, когда A и B оба True или оба False. Функция возвращает True, если все аргументы логически эквивалентны. В противном случае возвращает False.

>>> from sympy import * 
>>> from sympy.logic.boolalg import Equivalent 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Equivalent(a,b), Equivalent(a,c)

Приведенный выше фрагмент кода дает следующий результат -

(Ложь Правда)

Функция ITE

Эта функция действует как предложение If then else в языке программирования. Site (A, B, C) оценивает и возвращает результат B, если A истинно, иначе он возвращает результат C. Все аргументы должны быть логическими.

>>> from sympy import * >>> from sympy.logic.boolalg import ITE >>> a,b,c=symbols('a b c') >>> a,b,c=(True, False, True) 
>>> ITE(a,b,c), ITE(a,c,b)

Приведенный выше фрагмент кода дает следующий результат -

(Ложь Правда)

Модуль предположений в пакете SymPy содержит инструменты для извлечения информации о выражениях. Для этого модуль определяет функцию ask ().

sympy.assumptions.ask(property)

Следующие свойства предоставляют полезную информацию о выражении -

algebraic(x)

Чтобы быть алгебраическим, число должно быть корнем ненулевого полиномиального уравнения с рациональными коэффициентами. √2, потому что √2 является решением x2 - 2 = 0, поэтому оно алгебраическое.

complex(x)

Предикат комплексного числа. Это верно тогда и только тогда, когда x принадлежит набору комплексных чисел.

composite(x)

Предикат составного числа, возвращаемый функцией ask (Q.composite (x)), истинен тогда и только тогда, когда x является положительным целым числом и имеет по крайней мере один положительный делитель, отличный от 1 и самого числа.

even, odd

Метод ask () возвращает true, если x находится в наборе четных чисел и наборе нечетных чисел соответственно.

imaginary

Это свойство представляет предикат мнимого числа. Это правда, если x можно записать как действительное число, умноженное на мнимую единицу I.

integer

Это свойство, возвращаемое Q.integer (x), возвращает истину, если x принадлежит набору четных чисел.

rational, irrational

Q.irrational (x) истинно тогда и только тогда, когда x - любое действительное число, которое не может быть выражено как отношение целых чисел. Например, пи - иррациональное число.

positive, negative

Предикаты для проверки положительного или отрицательного числа

zero, nonzero

Предикаты для проверки, равно ли число нулю или нет

>>> from sympy import * 
>>> x=Symbol('x') 
>>> x=10 
>>> ask(Q.algebraic(pi))
False
>>> ask(Q.complex(5-4*I)), ask( Q.complex(100))
(True, True)
>>> x,y=symbols("x y") 
>>> x,y=5,10 
>>> ask(Q.composite(x)), ask(Q.composite(y))
(False, True)
>>> ask(Q.even(x)), ask(Q.even(y))
(False, True)
>>> x,y= 2*I, 4+5*I 
>>> ask(Q.imaginary(x)), ask(Q.imaginary(y))
(True, False)
>>> x,y=5,10 
>>> ask(Q.even(x)), ask(Q.even(y)), ask(Q.odd(x)), ask(Q.odd(y))
(False, True, True, False)
>>> x,y=5,-5 
>>> ask(Q.positive(x)), ask(Q.negative(y)), ask(Q.positive(x)), ask(Q.negative(y))
(True, True, True, True)
>>> ask(Q.rational(pi)), ask(Q.irrational(S(2)/3))
(False, False)
>>> ask(Q.zero(oo)), ask(Q.nonzero(I))
(False, False)

Sympy обладает мощной способностью упрощать математические выражения. В SymPy есть много функций для выполнения различного рода упрощений. Существует общая функция, называемая simpleify (), которая пытается получить простейшую форму выражения.

упрощать

Эта функция определена в модуле sympy.simplify. simpleify () пытается применить интеллектуальную эвристику, чтобы сделать входное выражение «проще». Следующий код показывает упрощенное выражение$sin^2(x)+cos^2(x)$.

>>> from sympy import * 
>>> x=Symbol('x')
>>> expr=sin(x)**2 + cos(x)**2 
>>> simplify(expr)

Приведенный выше фрагмент кода дает следующий результат -

1

расширять

Expand () - одна из наиболее распространенных функций упрощения в SymPy, используемая для раскрытия полиномиальных выражений. Например -

>>> a,b=symbols('a b') 
>>> expand((a+b)**2)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$a^2 + 2ab + b^2$

>>> expand((a+b)*(a-b))

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$a^2 - b^2$

Функция expand () делает выражения больше, а не меньше. Обычно это так, но часто выражение становится меньше после вызова для него метода expand ().

>>> expand((x + 1)*(x - 2) - (x - 1)*x)

Приведенный выше фрагмент кода дает следующий результат -

-2

фактор

Эта функция берет многочлен и разлагает его на неприводимые множители по рациональным числам.

>>> x,y,z=symbols('x y z') 
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
>>> factor(expr)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$z(x + 2y)^2$

>>> factor(x**2+2*x+1)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$(x + 1)^2$

Функция factor () противоположна функции expand (). Каждый из факторов, возвращаемых функцией factor (), гарантированно несократим. Функция factor_list () возвращает более структурированный вывод.

>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
>>> factor_list(expr)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

(1, [(z, 1), (x + 2*y, 2)])

собирать

Эта функция собирает дополнительные члены выражения относительно списка выражений с точностью до степеней с рациональными показателями.

>>> expr=x*y + x - 3 + 2*x**2 - z*x**2 + x**3 
>>> expr

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x^3 + x^2z + 2x^2 + xy + x - 3$

Функция collect () для этого выражения приводит к следующему:

>>> collect(expr,x)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x^3 + x^2(2 - z) + x(y + 1) - 3$

>>> expr=y**2*x + 4*x*y*z + 4*y**2*z+y**3+2*x*y 
>>> collect(expr,y)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$Y^3+Y^2(x+4z)+y(4xz+2x)$

отменить

Функция cancel () принимает любую рациональную функцию и преобразует ее в стандартную каноническую форму, p / q, где p и q - расширенные многочлены без общих множителей. Старшие коэффициенты p и q не имеют знаменателей, т. Е. Являются целыми числами.

>>> expr1=x**2+2*x+1 
>>> expr2=x+1 
>>> cancel(expr1/expr2)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x+1$

>>> expr = 1/x + (3*x/2 - 2)/(x - 4) 
>>> expr

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\frac{\frac{3x}{2} - 2}{x - 4} + \frac{1}{x}$

>>> cancel(expr)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\frac{3x^2 - 2x - 8}{2x^2 - 8}$

>>> expr=1/sin(x)**2 
>>> expr1=sin(x) 
>>> cancel(expr1*expr)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\frac{1}{\sin(x)}$

trigsimp

Эта функция используется для упрощения тригонометрических тождеств. Можно отметить, что соглашения об именах для обратных тригонометрических функций заключаются в добавлении a перед именем функции. Например, обратный косинус или арккосинус называется acos ().

>>> from sympy import trigsimp, sin, cos 
>>> from sympy.abc import x, y
>>> expr = 2*sin(x)**2 + 2*cos(x)**2 
>>> trigsimp(expr)

2

Функция trigsimp использует эвристику для применения наиболее подходящего тригонометрического тождества.

Powersimp

Эта функция уменьшает данное выражение, комбинируя степени с аналогичными основаниями и показателями.

>>> expr=x**y*x**z*y**z 
>>> expr

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x^y x^z y^z$

>>> powsimp(expr)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x^{y+z} y^z$

Вы можете заставить powsimp () объединять только базы или только показатели, изменяя comb = 'base' или comb = 'exp'. По умолчанию Combine = 'all' делает и то, и другое. Если force имеет значение True, базы будут объединены без проверки предположений.

>>> powsimp(expr, combine='base', force=True)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x^y(xy)^z$

гребешок

Комбинаторные выражения, включающие факториал и биномы, можно упростить с помощью функции combsimp (). SymPy предоставляет функцию factorial ()

>>> expr=factorial(x)/factorial(x - 3) 
>>> expr

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\frac{x!}{(x - 3)!}$

Чтобы упростить приведенное выше комбинаторное выражение, мы используем функцию combsimp () следующим образом:

>>> combsimp(expr)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x(x-2)(x-1)$

Бином (x, y) - это количество способов выбрать y элементов из набора x различных элементов. Его также часто пишут как xCy.

>>> binomial(x,y)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$(\frac{x}{y})$

>>> combsimp(binomial(x+1, y+1)/binomial(x, y))

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\frac{x + 1}{y + 1}$

бревенчатый комбайн

Эта функция берет логарифмы и объединяет их, используя следующие правила:

• log (x) + log (y) == log (x * y), если оба положительны
• a * log (x) == log (x ** a), если x положительно, а a реально

>>> logcombine(a*log(x) + log(y) - log(z))

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$a\log(x) + \log(y) - \log(z)$

Если для параметра силы этой функции установлено значение True, то предположения, приведенные выше, будут считаться выполненными, если уже не существует предположений относительно количества.

>>> logcombine(a*log(x) + log(y) - log(z), force=True)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\log\frac{x^a y}{z}$

Производная функции - это мгновенная скорость изменения одной из переменных. Это эквивалентно нахождению наклона касательной к функции в точке. Мы можем найти дифференцирование математических выражений в форме переменных, используя функцию diff () в пакете SymPy.

diff(expr, variable)
>>> from sympy import diff, sin, exp 
>>> from sympy.abc import x,y 
>>> expr=x*sin(x*x)+1 >>> expr

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x\sin(x^2) + 1$

>>> diff(expr,x)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$2x^2\cos(x^2) + \sin(x^2)$

>>> diff(exp(x**2),x)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

2xe^x2

Чтобы взять несколько производных, передайте переменную столько раз, сколько хотите дифференцировать, или передайте число после переменной.

>>> diff(x**4,x,3)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$24x$

>>> for i in range(1,4): print (diff(x**4,x,i))

Приведенный выше фрагмент кода дает следующее выражение -

4*x**3

12*x**2

24*x

Также можно вызвать метод diff () выражения. Работает аналогично функции diff ().

>>> expr=x*sin(x*x)+1 
>>> expr.diff(x)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$2x^2\cos(x^2) + \sin(x^2)$

Неоцененный производный инструмент создается с использованием класса Derivative. Он имеет тот же синтаксис, что и функция diff (). Чтобы оценить неоцененную производную, используйте метод doit.

>>> from sympy import Derivative 
>>> d=Derivative(expr) 
>>> d

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\frac{d}{dx}(x\sin(x^2)+1)$

>>> d.doit()

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$2x^2\cos(x^2) + \sin(x^2)$

Пакет SymPy содержит модуль интегралов. В нем реализованы методы вычисления определенных и неопределенных интегралов выражений. Метод интегрировать () используется для вычисления как определенных, так и неопределенных интегралов. Чтобы вычислить неопределенный или примитивный интеграл, просто передайте переменную после выражения.

Например -

integrate(f, x)

Чтобы вычислить определенный интеграл, передайте аргумент следующим образом:

(integration_variable, lower_limit, upper_limit)

>>> from sympy import * 
>>> x,y = symbols('x y') 
>>> expr=x**2 + x + 1 
>>> integrate(expr, x)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\frac{x^3}{3} + \frac{x^2}{2} + x$

>>> expr=sin(x)*tan(x) 
>>> expr 
>>> integrate(expr,x)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$-\frac{\log(\sin(x) - 1)}{2} + \frac{\log(\sin(x) + 1)}{2} - \sin(x)$

Пример определенного интеграла приведен ниже -

>>> expr=exp(-x**2) 
>>> integrate(expr,(x,0,oo) )

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\frac{\sqrt\pi}{2}$

Вы можете передать несколько предельных кортежей для выполнения множественного интеграла. Пример приведен ниже -

>>> expr=exp(-x**2 - y**2)
>>> integrate(expr,(x,0,oo),(y,0,oo))

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\frac{\pi}{4}$

Вы можете создать неоцененный интеграл с помощью объекта Integral, который можно оценить, вызвав метод doit ().

>>> expr = Integral(log(x)**2, x) 
>>> expr

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\int \mathrm\log(x)^2 \mathrm{d}x$

>>> expr.doit()

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x\log(x)^2 - 2xlog(x) + 2x$

Интегральные преобразования

SymPy поддерживает различные типы интегральных преобразований следующим образом:

• laplace_transform
• fourier_transform
• sine_transform
• cosine_transform
• hankel_transform

Эти функции определены в модуле sympy.integrals.transforms. Следующие примеры вычисляют преобразование Фурье и преобразование Лапласа соответственно.

Example 1

>>> from sympy import fourier_transform, exp 
>>> from sympy.abc import x, k 
>>> expr=exp(-x**2) 
>>> fourier_transform(expr, x, k)

При выполнении вышеуказанной команды в оболочке python будет сгенерирован следующий вывод:

sqrt(pi)*exp(-pi**2*k**2)

Что эквивалентно -

$\sqrt\pi * e^{\pi^2k^2}$

Example 2

>>> from sympy.integrals import laplace_transform 
>>> from sympy.abc import t, s, a 
>>> laplace_transform(t**a, t, s)

При выполнении вышеуказанной команды в оболочке python будет сгенерирован следующий вывод:

(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)

В математике матрица - это двумерный массив чисел, символов или выражений. Теория манипуляций с матрицами занимается выполнением арифметических операций над матричными объектами при соблюдении определенных правил.

Линейное преобразование - одно из важных приложений матриц. Многие научные области, особенно связанные с физикой, используют приложения, связанные с матрицами.

В пакете SymPy есть модуль матриц, который занимается обработкой матриц. Он включает класс Matrix, объект которого представляет собой матрицу.

Note: If you want to execute all the snippets in this chapter individually, you need to import the matrix module as shown below −

>>> from sympy.matrices import Matrix

Example

>>> from sympy.matrices import Matrix 
>>> m=Matrix([[1,2,3],[2,3,1]]) 
>>> m
$\displaystyle \left[\begin{matrix}1 & 2 & 3\\2 & 3 & 1\end{matrix}\right]$

При выполнении вышеуказанной команды в оболочке python будет сгенерирован следующий вывод:

[1 2 3 2 3 1]

Матрица создается из объектов List соответствующего размера. Вы также можете получить матрицу, распределив элементы списка по заданному количеству строк и столбцов.

>>> M=Matrix(2,3,[10,40,30,2,6,9]) 
>>> M
$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$

При выполнении вышеуказанной команды в оболочке python будет сгенерирован следующий вывод:

[10 40 30 2 6 9]

Матрица - изменяемый объект. Модуль матриц также предоставляет класс ImmutableMatrix для получения неизменяемой матрицы.

Основные манипуляции

В shape Свойство объекта Matrix возвращает его размер.

>>> M.shape

Вывод для приведенного выше кода выглядит следующим образом:

(2,3)

Методы row () и col () соответственно возвращают строку или столбец указанного числа.

>>> M.row(0)
$\displaystyle \left[\begin{matrix}10 & 40 & 30\end{matrix}\right]$

Вывод для приведенного выше кода выглядит следующим образом:

[10 40 30]

>>> M.col(1)
$\displaystyle \left[\begin{matrix}40\\6\end{matrix}\right]$

Вывод для приведенного выше кода выглядит следующим образом:

[40 6]

Используйте оператор среза Python для извлечения одного или нескольких элементов, принадлежащих строке или столбцу.

>>> M.row(1)[1:3]
[6, 9]

Класс Matrix имеет методы row_del () и col_del (), которые удаляют указанную строку / столбец из данной матрицы -

>>> M=Matrix(2,3,[10,40,30,2,6,9]) 
>>> M.col_del(1) 
>>> M

При выполнении вышеуказанной команды в оболочке python будет сгенерирован следующий вывод:

Matrix([[10, 30],[ 2, 9]])

Вы можете применить стиль к выводу, используя следующую команду -

$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$

После выполнения приведенного выше фрагмента кода вы получите следующий результат:

[10 30 2 9]

>>> M.row_del(0) 
>>> M

$\displaystyle \left[\begin{matrix}2 & 9\end{matrix}\right]$

После выполнения приведенного выше фрагмента кода вы получите следующий результат:

[2 9]

Точно так же методы row_insert () и col_insert () добавляют строки или столбцы по указанному индексу строки или столбца.

>>> M1=Matrix([[10,30]]) 
>>> M=M.row_insert(0,M1)
>>> M

$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$

После выполнения приведенного выше фрагмента кода вы получите следующий результат:

[10 40 30 2 9]

>>> M2=Matrix([40,6]) 
>>> M=M.col_insert(1,M2) 
>>> M

$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$

После выполнения приведенного выше фрагмента кода вы получите следующий результат:

[10 40 30 6 9]

Арифметические операции

Обычные операторы +, - и * определены для выполнения сложения, вычитания и умножения.

>>> M1=Matrix([[1,2,3],[3,2,1]]) 
>>> M2=Matrix([[4,5,6],[6,5,4]]) 
>>> M1+M2

$\displaystyle \left[\begin{matrix}5 & 7 & 9\\9 & 7 & 5\end{matrix}\right]$

После выполнения приведенного выше фрагмента кода вы получите следующий результат:

[5 7 9 9 7 5]

>>> M1-M2
$\displaystyle \left[\begin{matrix}-3 & -3 & -3\\-3 & -3 & -3\end{matrix}\right]$

После выполнения приведенного выше фрагмента кода вы получите следующий результат:

[- 3 -3 -3 -3 -3 -3]

Умножение матриц возможно только в том случае, если - Количество столбцов 1-й матрицы должно равняться количеству строк 2-й матрицы. - И результат будет иметь то же количество строк, что и первая матрица, и такое же количество столбцов, как и вторая матрица.

>>> M1=Matrix([[1,2,3],[3,2,1]]) 
>>> M2=Matrix([[4,5],[6,6],[5,4]]) 
>>> M1*M2
$\displaystyle \left[\begin{matrix}31 & 29\\29 & 31\end{matrix}\right]$

Вывод для приведенного выше кода выглядит следующим образом:

[31 29 29 31]

>>> M1.T
$\displaystyle \left[\begin{matrix}1 & 3\\2 & 2\\3 & 1\end{matrix}\right]$

После выполнения кода получается следующий вывод -

[1 3 2 2 3 1]

Для вычисления определителя матрицы используйте метод det (). Определитель - это скалярное значение, которое может быть вычислено из элементов квадратной матрицы.

>>> M=Matrix(3,3,[10,20,30,5,8,12,9,6,15])
>>> M
$\displaystyle \left[\begin{matrix}10 & 20 & 30\\5 & 8 & 12\\9 & 6 & 15\end{matrix}\right]$

Вывод для приведенного выше кода выглядит следующим образом:

[10 20 30 5 8 12 9 6 15]

>>> M.det()

Вывод для приведенного выше кода выглядит следующим образом:

-120

Матричные конструкторы

SymPy предоставляет множество специальных типов матричных классов. Например, матрица идентичности, матрица всех нулей и единиц и т.д. Эти классы называются глазами, нулями и единицами соответственно. Матрица идентичности - это квадратная матрица, элементы которой по диагонали равны 1, остальные элементы равны 0.

Example

from sympy.matrices import eye eye(3)

Output

Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])

$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right]$

Вывод для приведенного выше кода выглядит следующим образом:

[1 0 0 0 1 0 0 0 1]

В матрице diag элементы по диагонали инициализируются в соответствии с предоставленными аргументами.

>>> from sympy.matrices import diag 
>>> diag(1,2,3)

$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 2 & 0\\0 & 0 & 3\end{matrix}\right]$

Вывод для приведенного выше кода выглядит следующим образом:

[1 0 0 0 2 0 0 0 3]

Все элементы в нулевой матрице инициализируются нулем.

>>> from sympy.matrices import zeros 
>>> zeros(2,3)

$\displaystyle \left[\begin{matrix}0 & 0 & 0\\0 & 0 & 0\end{matrix}\right]$

Вывод для приведенного выше кода выглядит следующим образом:

[0 0 0 0 0 0]

Аналогично, единицы - это матрица, в которой все элементы установлены в 1.

>>> from sympy.matrices import ones
>>> ones(2,3)

$\displaystyle \left[\begin{matrix}1 & 1 & 1\\1 & 1 & 1\end{matrix}\right]$

Вывод для приведенного выше кода выглядит следующим образом:

[1 1 1 1 1 1]

Пакет Sympy имеет класс Function, который определен в модуле sympy.core.function. Это базовый класс для всех прикладных математических функций, а также конструктор для неопределенных классов функций.

Следующие категории функций унаследованы от класса Function -

• Функции для комплексного числа
• Тригонометрические функции
• Функции для целого числа
• Комбинаторные функции
• Прочие разные функции

Функции для комплексного числа

Этот набор функций определен в sympy.functions.elementary.complexes модуль.

re

Эта функция возвращает действительную часть выражения -

>>> from sympy import * 
>>> re(5+3*I)

Вывод для приведенного выше фрагмента кода приведен ниже -

5

>>> re(I)

Вывод для приведенного выше фрагмента кода -

0

Im

Эта функция возвращает мнимую часть выражения -

>>> im(5+3*I)

Вывод для приведенного выше фрагмента кода приведен ниже -

3

>>> im(I)

Вывод для приведенного выше фрагмента кода приведен ниже -

1

sign

Эта функция возвращает комплексный знак выражения.

Для реального выражения знак будет -

• 1, если выражение положительное
• 0, если выражение равно нулю
• -1, если выражение отрицательное

Если выражение мнимое, возвращается знак -

• I, если im (выражение) положительно
• -I, если im (выражение) отрицательное

>>> sign(1.55), sign(-1), sign(S.Zero)

Вывод для приведенного выше фрагмента кода приведен ниже -

(1, -1, 0)

>>> sign (-3*I), sign(I*2)

Вывод для приведенного выше фрагмента кода приведен ниже -

(-I, I)

Abs

Эта функция возвращает абсолютное значение комплексного числа. Он определяется как расстояние между началом координат (0,0) и точкой (a, b) на комплексной плоскости. Эта функция является расширением встроенной функции abs () для приема символьных значений.

>>> Abs(2+3*I)

Вывод для приведенного выше фрагмента кода приведен ниже -

$\sqrt13$

conjugate

Эта функция возвращает конъюгат комплексного числа. Чтобы найти комплексное сопряжение, мы меняем знак мнимой части.

>>> conjugate(4+7*I)

После выполнения приведенного выше фрагмента кода вы получите следующий результат:

4 - 7i

Тригонометрические функции

SymPy имеет определения для всех тригонометрических соотношений - sin cos, tan и т. Д., А также их обратные аналоги, такие как asin, acos, atan и т. Д. Эти функции вычисляют соответствующее значение для заданного угла, выраженного в радианах.

>>> sin(pi/2), cos(pi/4), tan(pi/6)

Вывод для приведенного выше фрагмента кода приведен ниже -

(1, sqrt(2)/2, sqrt(3)/3)

>>> asin(1), acos(sqrt(2)/2), atan(sqrt(3)/3)

Вывод для приведенного выше фрагмента кода приведен ниже -

(pi/2, pi/4, pi/6)

Функции над целым числом

Это набор функций для выполнения различных операций с целым числом.

ceiling

Это одномерная функция, которая возвращает наименьшее целочисленное значение, не меньшее, чем его аргумент. В случае комплексных чисел потолок действительной и мнимой частей отдельно.

>>> ceiling(pi), ceiling(Rational(20,3)), ceiling(2.6+3.3*I)

Вывод для приведенного выше фрагмента кода приведен ниже -

(4, 7, 3 + 4*I)

floor

Эта функция возвращает наибольшее целочисленное значение, не превышающее ее аргумент. В случае комплексных чисел эта функция также использует отдельно действительную и мнимую части.

>>> floor(pi), floor(Rational(100,6)), floor(6.3-5.9*I)

Вывод для приведенного выше фрагмента кода приведен ниже -

(3, 16, 6 - 6*I)

frac

Эта функция представляет собой дробную часть x.

>>> frac(3.99), frac(Rational(10,3)), frac(10)

Вывод для приведенного выше фрагмента кода приведен ниже -

(0.990000000000000, 1/3, 0)

Комбинаторные функции

Комбинаторика - это область математики, занимающаяся проблемами выбора, расположения и работы в конечной или дискретной системе.

factorial

Факториал очень важен в комбинаторике, где он дает количество способов, которыми могут быть переставлены n объектов. Это символически представлено как ð ?? '¥! Эта функция является реализацией функции факториала по неотрицательным целым числам, факториал отрицательного целого числа - комплексная бесконечность.

>>> x=Symbol('x') 
>>> factorial(x)

Вывод для приведенного выше фрагмента кода приведен ниже -

x!

>>> factorial(5)

Вывод для приведенного выше фрагмента кода приведен ниже -

120

>>> factorial(-1)

Вывод для приведенного выше фрагмента кода приведен ниже -

$\infty\backsim$

биномиальный

Эта функция определяет количество способов, которыми мы можем выбрать k элементов из набора n элементов.

>>> x,y=symbols('x y') 
>>> binomial(x,y)

Вывод для приведенного выше фрагмента кода приведен ниже -

$(\frac{x}{y})$

>>> binomial(4,2)

Вывод для приведенного выше фрагмента кода приведен ниже -

6

Строки треугольника Паскаля могут быть созданы с помощью биномиальной функции.

>>> for i in range(5): print ([binomial(i,j) for j in range(i+1)])

После выполнения приведенного выше фрагмента кода вы получите следующий результат:

[1]

[1, 1]

[1, 2, 1]

[1, 3, 3, 1]

[1, 4, 6, 4, 1]

fibonacci

Числа Фибоначчи - это целочисленная последовательность, определяемая начальными членами F0 = 0, F1 = 1 и двухчленным рекуррентным соотношением Fn = Fnâˆ'1 + Fnâˆ'2.

>>> [fibonacci(x) for x in range(10)]

Следующий результат получается после выполнения приведенного выше фрагмента кода -

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]

tribonacci

Числа Трибоначчи представляют собой целочисленную последовательность, определяемую начальными членами F0 = 0, F1 = 1, F2 = 1 и трехчленным рекуррентным соотношением Fn = Fn-1 + Fn-2 + Fn-3.

>>> tribonacci(5, Symbol('x'))

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x^8 + 3x^5 + 3x^2$

>>> [tribonacci(x) for x in range(10)]

Следующий результат получается после выполнения приведенного выше фрагмента кода -

[0, 1, 1, 2, 4, 7, 13, 24, 44, 81]

Разные функции

Ниже приведен список некоторых часто используемых функций -

Min- Возвращает минимальное значение списка. Он назван Min, чтобы избежать конфликтов со встроенной функцией min.

Max- Возвращает максимальное значение списка. Он назван Max, чтобы избежать конфликтов со встроенной функцией max.

root - Возвращает корень n-й степени из x.

sqrt - Возвращает главный квадратный корень из x.

cbrt - Эта функция вычисляет главный кубический корень из x (сокращение для x ++ Rational (1,3)).

Ниже приведены примеры перечисленных выше различных функций и их соответствующих выходов.

>>> Min(pi,E)

e

>>> Max(5, Rational(11,2))

$\frac{11}{2}$

>>> root(7,Rational(1,2))

49

>>> sqrt(2)

$\sqrt2$

>>> cbrt(1000)

10

В математике система счисления Quaternion - это расширение комплексных чисел. Каждый объект Quaternion содержит четыре скалярные переменные и четыре измерения, одно реальное измерение и три мнимых измерения.

Кватернион представлен следующим выражением -

q = a + bi + cj + dk

где a, b, c и d - действительные числа и i, j, k являются кватернионными единицами, такими что i2 == j2 == k2 == ijk

В sympy.algebras.quaternion модуль имеет класс Quaternion.

>>> from sympy.algebras.quaternion import Quaternion 
>>> q=Quaternion(2,3,1,4) 
>>> q

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$2 + 3i + 1j + 4k$

Кватернионы используются в чистой математике, а также в прикладной математике, компьютерной графике, компьютерном зрении и т. Д.

>>> from sympy import * 
>>> x=Symbol('x') 
>>> q1=Quaternion(x**2, x**3, x) >>> q1

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$x^2 + x^3i + xj + 0k$

Объект Quaternion также может иметь мнимые коэффициенты

>>> q2=Quaternion(2,(3+2*I), x**2, 3.5*I) 
>>> q2

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$2 + (3 + 2i)i + x2j + 3.5ik$

Добавить()

Этот метод, доступный в классе Quaternion, выполняет добавление двух объектов Quaternion.

>>> q1=Quaternion(1,2,3,4) 
>>> q2=Quaternion(4,3,2,1) 
>>> q1.add(q2)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$5 + 5i + 5j + 5k$

В объект Quaternion можно добавить число или символ.

>>> q1+2

Следующий результат получается после выполнения приведенного выше фрагмента кода -

$3 + 2i + 3j + 4k$

>>> q1+x

Следующий результат получается после выполнения приведенного выше фрагмента кода -

$(x + 1) + 2i + 3j + 4k$

mul ()

Этот метод выполняет умножение двух кватернионных объектов.

>>> q1=Quaternion(1,2,1,2) 
>>> q2=Quaternion(2,4,3,1) 
>>> q1.mul(q2)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$(-11) + 3i + 11j + 7k$

обратный ()

Этот метод возвращает инверсию объекта кватерниона.

>>> q1.inverse()

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\frac{1}{10} + (-\frac{1}{5})i + (-\frac{1}{10})j + (-\frac{1}{5})k$

pow ()

Этот метод возвращает мощность объекта кватерниона.

>>> q1.pow(2)

Следующий результат получается после выполнения приведенного выше фрагмента кода -

$(-8) + 4i + 2j + 4k$

exp ()

Этот метод вычисляет экспоненту объекта Quaternion, т.е. eq

>>> q=Quaternion(1,2,4,3) 
>>> q.exp()

Следующий результат получается после выполнения приведенного выше фрагмента кода -

$e\cos(\sqrt29) + \frac{2\sqrt29e\sin(\sqrt29)}{29}i + \frac{4\sqrt29e\sin(\sqrt29)}{29}j + \frac{3\sqrt29e\sin}{29}k$

Поскольку символы = и == определены в Python как операторы присваивания и равенства, их нельзя использовать для формулирования символьных уравнений. SymPy предоставляет функцию Eq () для создания уравнения.

>>> from sympy import * 
>>> x,y=symbols('x y') 
>>> Eq(x,y)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

x = y

Поскольку x = y возможно тогда и только тогда, когда xy = 0, приведенное выше уравнение может быть записано как -

>>> Eq(x-y,0)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

x − y = 0

Модуль решателя в SymPy предоставляет функцию soveset (), прототип которой выглядит следующим образом:

solveset(equation, variable, domain)

Домен по умолчанию S.Complexes. Используя функцию resolveset (), мы можем решить алгебраическое уравнение следующим образом:

>>> solveset(Eq(x**2-9,0), x)

Получен следующий результат -

{−3, 3}

>>> solveset(Eq(x**2-3*x, -2),x)

Следующий результат получается после выполнения приведенного выше фрагмента кода -

{1,2}

Результатом набора решений является FiniteSet решений. Если решений нет, возвращается EmptySet.

>>> solveset(exp(x),x)

Следующий результат получается после выполнения приведенного выше фрагмента кода -

$\varnothing$

Линейное уравнение

Мы должны использовать функцию linsolve () для решения линейных уравнений.

Например, уравнения следующие:

ху = 4

х + у = 1

>>> from sympy import * 
>>> x,y=symbols('x y') 
>>> linsolve([Eq(x-y,4),Eq( x + y ,1) ], (x, y))

Следующий результат получается после выполнения приведенного выше фрагмента кода -

$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$

Функция linsolve () также может решать линейные уравнения, выраженные в матричной форме.

>>> a,b=symbols('a b') 
>>> a=Matrix([[1,-1],[1,1]]) 
>>> b=Matrix([4,1]) 
>>> linsolve([a,b], (x,y))

Мы получим следующий результат, если выполним приведенный выше фрагмент кода -

$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$

Нелинейное уравнение

Для этого мы используем функцию nonlinsolve (). Уравнения для этого примера -

а ² + а = 0 ab = 0

>>> a,b=symbols('a b') 
>>> nonlinsolve([a**2 + a, a - b], [a, b])

Мы получим следующий результат, если выполним приведенный выше фрагмент кода -

$\lbrace(-1, -1),(0,0)\rbrace$

дифференциальное уравнение

Сначала создайте неопределенную функцию, передав cls = Function функции символов. Чтобы решить дифференциальные уравнения, используйте dsolve.

>>> x=Symbol('x') 
>>> f=symbols('f', cls=Function) 
>>> f(x)

Следующий результат получается после выполнения приведенного выше фрагмента кода -

f(x)

Здесь f (x) - неоцененная функция. Его производная следующая -

>>> f(x).diff(x)

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$\frac{d}{dx}f(x)$

Сначала мы создаем объект Eq, соответствующий следующему дифференциальному уравнению

>>> eqn=Eq(f(x).diff(x)-f(x), sin(x)) 
>>> eqn

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$-f(x) + \frac{d}{dx}f(x)= \sin(x)$

>>> dsolve(eqn, f(x))

Приведенный выше фрагмент кода дает результат, эквивалентный приведенному ниже выражению -

$f(x)=(c^1-\frac{e^-xsin(x)}{2}-\frac{e^-xcos(x)}{2})e^x$

SymPy использует библиотеку Matplotlib в качестве бэкэнда для визуализации 2-D и 3-D графиков математических функций. Убедитесь, что Matplotlib доступен в текущей установке Python. Если нет, установите то же самое, используя следующую команду -

pip install matplotlib

Поддержка печати определяется в модуле sympy.plotting. Следующие функции присутствуют в модуле построения графиков -

• plot - 2D линейные графики

• plot3d - трехмерные линейные графики

• plot_parametric - 2D параметрические графики

• plot3d_parametric - 3D параметрические графики

Функция plot () возвращает экземпляр класса Plot. Фигура графика может иметь одно или несколько выражений SymPy. Хотя он может использовать Matplotlib в качестве бэкэнда, также могут использоваться другие бэкэнды, такие как texplot, pyglet или Google charts API.

plot(expr, range, kwargs)

где expr - любое допустимое выражение symPy. Если не указано иное, для диапазона используется значение по умолчанию (-10, 10).

В следующем примере показаны значения x2 для каждого значения в диапазоне (-10,10) -

>>> from sympy.plotting import plot 
>>> from sympy import * 
>>> x=Symbol('x') 
>>> plot(x**2, line_color='red')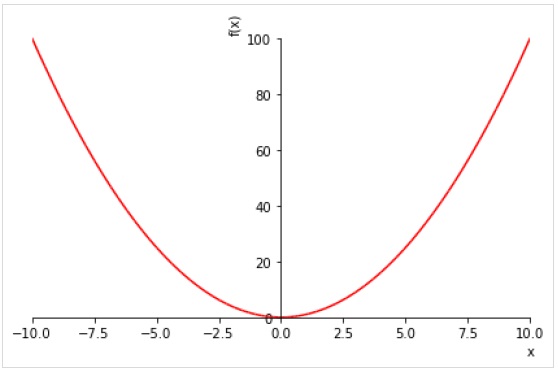

Чтобы нарисовать несколько графиков для одного и того же диапазона, перед кортежем диапазона укажите несколько выражений.

>>> plot( sin(x),cos(x), (x, -pi, pi))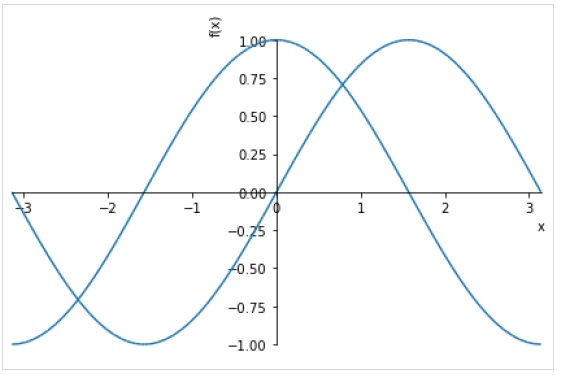

Вы также можете указать отдельный диапазон для каждого выражения.

plot((expr1, range1), (expr2, range2))

На следующем рисунке показаны графики sin (x) и cos (x) в разных диапазонах.

>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)))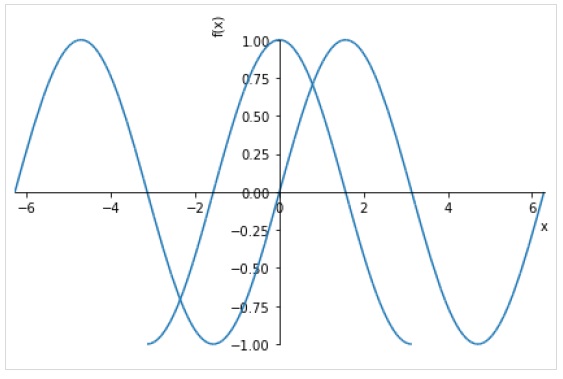

В функции plot () могут быть указаны следующие необязательные аргументы ключевого слова.

• line_color - определяет цвет линии графика.

• title - строка, которая будет отображаться как заголовок

• xlabel - строка, которая будет отображаться как метка для оси X

• ylabel - строка, которая будет отображаться как метка для оси y

>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)), line_color='red', title='SymPy plot example')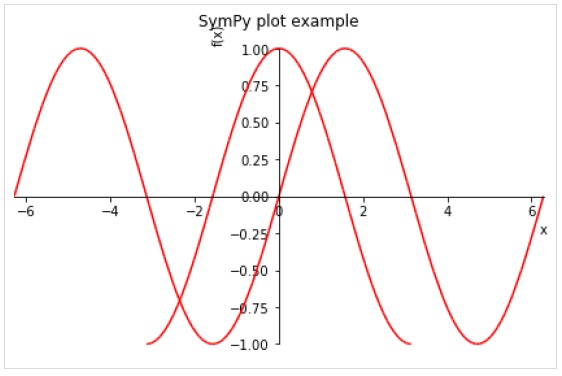

Функция plot3d () отображает трехмерный график.

plot3d(expr, xrange, yrange, kwargs)

В следующем примере рисуется трехмерный график поверхности -

>>> from sympy.plotting import plot3d 
>>> x,y=symbols('x y') 
>>> plot3d(x*y, (x, -10,10), (y, -10,10))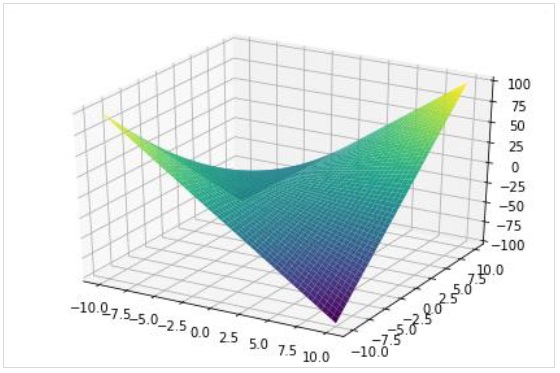

Как и в 2D-графике, на трехмерном графике также может быть несколько графиков, каждый с разным диапазоном.

>>> plot3d(x*y, x/y, (x, -5, 5), (y, -5, 5))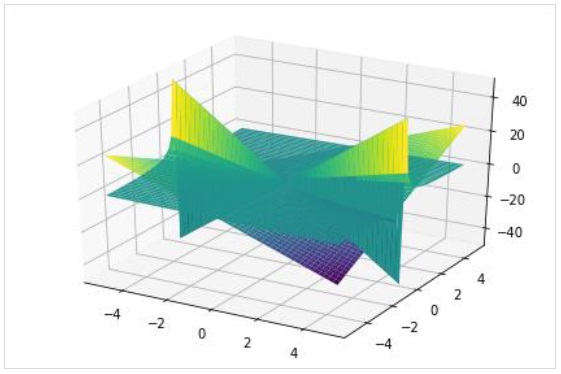

Функция plot3d_parametric_line () отображает 3-х мерный параметрический линейный график.

>>> from sympy.plotting import plot3d_parametric_line 
>>> plot3d_parametric_line(cos(x), sin(x), x, (x, -5, 5))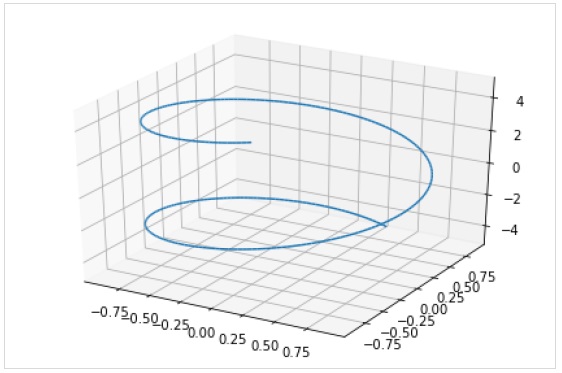

Чтобы нарисовать параметрический график поверхности, используйте функцию plot3d_parametric_surface ().

plot3d_parametric_surface(xexpr, yexpr, zexpr, rangex, rangey, kwargs)

>>> from sympy.plotting import plot3d_parametric_surface 
>>> plot3d_parametric_surface(cos(x+y), sin(x-y), x-y, (x, -5, 5), (y, -5, 5))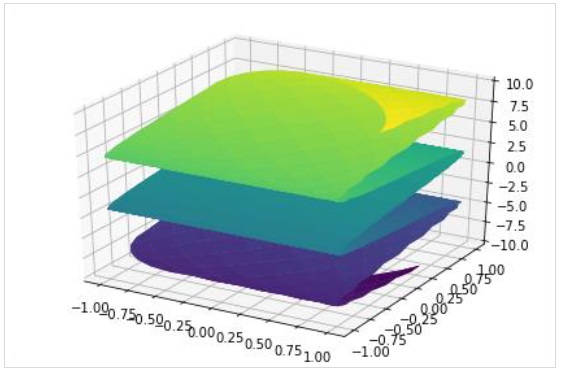

Модуль геометрии в SymPy позволяет создавать двухмерные объекты, такие как линия, круг и т. Д. Затем мы можем получить информацию о них, такую ​​как проверка коллинеарности или поиск пересечения.

Точка

Класс Point представляет собой точку в евклидовом пространстве. Следующий пример проверяет коллинеарность точек -

>>> from sympy.geometry import Point 
>>> from sympy import * 
>>> x=Point(0,0) 
>>> y=Point(2,2) 
>>> z=Point(4,4) 
>>> Point.is_collinear(x,y,z)

Output

True

>>> a=Point(2,3) 
>>> Point.is_collinear(x,y,a)

Output

False

Метод distance () класса Point вычисляет расстояние между двумя точками

>>> x.distance(y)

Output

$2\sqrt2$

Расстояние также может быть представлено в виде символов.

Линия

Линия получается из двух объектов Point. Метод crossction () возвращает точку пересечения, если две прямые пересекают друг друга.

>>> from sympy.geometry import Point, Line 
>>> p1, p2=Point(0,5), Point(5,0) 
>>> l1=Line(p1,p2)
>>> l2=Line(Point(0,0), Point(5,5)) 
>>> l1.intersection(l2)

Output

[Point2D(5/2, 5/2)]

>>> l1.intersection(Line(Point(0,0), Point(2,2)))

Output

[Point2D(5/2, 5/2)]

>>> x,y=symbols('x y') 
>>> p=Point(x,y) 
>>> p.distance(Point(0,0))

Output

$\sqrt{x^2 + y^2}$

Треугольник

Эта функция строит треугольник из трех точечных объектов.

Triangle(a,b,c)

>>> t=Triangle(Point(0,0),Point(0,5), Point(5,0)) 
>>> t.area

Output

$-\frac{25}{2}$

Эллипс

Сущность эллиптической геометрии создается путем передачи объекта Point, соответствующего центру, и двух чисел для горизонтального и вертикального радиуса.

ellipse(center, hradius, vradius)

>>> from sympy.geometry import Ellipse, Line 
>>> e=Ellipse(Point(0,0),8,3) 
>>> e.area

Output

$24\pi$

Врадиус может быть получен косвенно с помощью параметра эксцентриситета.

>>> e1=Ellipse(Point(2,2), hradius=5, eccentricity=Rational(3,4)) 
>>> e1.vradius

Output

$\frac{5\sqrt7}{4}$

В apoapsis эллипса - наибольшее расстояние между фокусом и контуром.

>>> e1.apoapsis

Output

$\frac{35}{4}$

Следующий оператор вычисляет окружность эллипса -

>>> e1.circumference

Output

$20E(\frac{9}{16})$

В equation метод эллипса возвращает уравнение эллипса.

>>> e1.equation(x,y)

Output

$(\frac{x}{5}-\frac{2}{5})^2 + \frac{16(y-2)2}{175} - 1$

В математике набор - это четко определенный набор различных объектов, которые могут быть числами, людьми, буквами алфавита или даже другими наборами. Set также является одним из встроенных типов в Python. SymPy предоставляет модуль наборов. Он содержит определения различных типов наборов и имеет функции для выполнения операций над наборами, таких как пересечение, объединение и т. Д.

Set - это базовый класс для любого другого типа набора в SymPy. Обратите внимание, что он отличается от типа данных встроенного набора Python. Класс Interval представляет реальные интервалы, а его граничное свойство возвращаетFiniteSet объект.

>>> from sympy import Interval 
>>> s=Interval(1,10).boundary 
>>> type(s)

sympy.sets.sets.FiniteSet

FiniteSet - это набор дискретных чисел. Его можно получить из любого объекта последовательности, такого как список или строка.

>>> from sympy import FiniteSet 
>>> FiniteSet(range(5))

Output

$\lbrace\lbrace0,1,...,4\rbrace\rbrace$

>>> numbers=[1,3,5,2,8] 
>>> FiniteSet(*numbers)

Output

$\lbrace1,2,3,5,8\rbrace$

>>> s="HelloWorld" 
>>> FiniteSet(*s)

Output

{H,W,d,e,l,o,r}

Обратите внимание, что, как и во встроенном наборе, набор SymPy также представляет собой набор отдельных объектов.

ConditionSet набор элементов, удовлетворяющих заданному условию

>>> from sympy import ConditionSet, Eq, Symbol 
>>> x=Symbol('x') 
>>> s=ConditionSet(x, Eq(x**2-2*x,0), Interval(1,10)) >>> s

Output

$\lbrace x\mid x\in[1,10]∧x^2 - 2x =0\rbrace$

Unionпредставляет собой составной набор. Он включает в себя все элементы в двух наборах. Обратите внимание, что элементы, которые есть в обоих, появятся в Союзе только один раз.

>>> from sympy import Union 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> Union(a,b)

Intersection с другой стороны, содержит только те элементы, которые присутствуют в обоих.

>>> from sympy import Intersection 
>>> Intersection(a,b)

ProductSet объект представляет собой декартово произведение элементов в обоих наборах.

>>> from sympy import ProductSet 
>>> l1=[1,2] 
>>> l2=[2,3] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> set(ProductSet(a,b))

Complement(a,b) сохраняет элементы в исключительных элементах, которые являются общими для набора b.

>>> from sympy import Complement 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> Complement(a,b), Complement(b,a)

SymmetricDifference набор содержит только необычные элементы в обоих наборах.

>>> from sympy import SymmetricDifference 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> SymmetricDifference(a,b)

Output

{2,3,5,9}

В SymPy доступно несколько принтеров. Ниже приводится частичный список -

• str
• srepr
• ASCII красивый принтер
• Unicode симпатичный принтер
• LaTeX
• MathML
• Dot

Объекты SymPy также можно отправлять в качестве вывода в код различных языков, таких как C, Fortran, Javascript, Theano и Python.

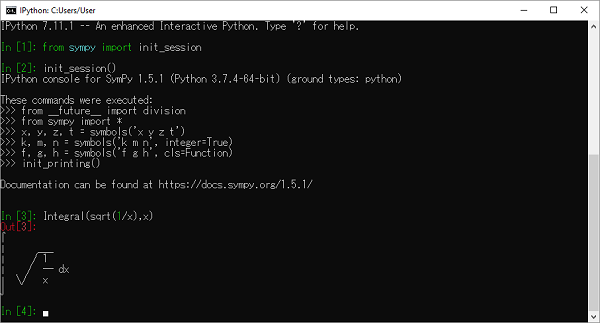
SymPy использует символы Unicode для вывода вывода в виде красивой печати. Если вы используете консоль Python для выполнения сеанса SymPy, лучшая красивая среда печати активируется вызовом функции init_session ().

>>> from sympy import init_session 
>>> init_session()

Консоль IPython для SymPy 1.5.1 (Python 3.7.4-64-бит) (основные типы: python).

Эти команды были выполнены -

>>> from __future__ import division
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()

Документацию можно найти на https://docs.sympy.org/1.5.1/.

>>> Integral(sqrt(1/x),x)

$\int \sqrt\frac{1}{x} dx$

Если LATEX не установлен, но установлен Matplotlib, он будет использовать механизм визуализации Matplotlib. Если Matplotlib не установлен, он использует симпатичный принтер Unicode. Однако блокнот Jupyter использует MathJax для рендеринга LATEX.

В терминале, который не поддерживает Unicode, используется симпатичный принтер ASCII.

Чтобы использовать принтер ASCII, используйте функцию pprint () со свойством use_unicode, установленным на False

>>> pprint(Integral(sqrt(1/x),x),use_unicode=False)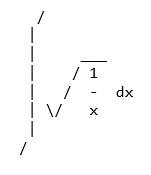

Доступ к симпатичному принтеру Unicode также осуществляется из pprint () и pretty (). Если терминал поддерживает Unicode, он используется автоматически. Если pprint () не может определить, что терминал поддерживает Unicode, вы можете передать use_unicode = True, чтобы заставить его использовать Unicode.

Чтобы получить LATEX-форму выражения, используйте функцию latex ().

>>> print(latex(Integral(sqrt(1/x),x)))

\int \sqrt{\frac{1}{x}}\, dx

Вы также можете использовать математический принтер. для этой цели импортируйте функцию print_mathml. Версия строки получается функцией mathml ().

>>> from sympy.printing.mathml import print_mathml 
>>> print_mathml(Integral(sqrt(1/x),x))

<apply>

<int/>

<bvar>

<ci>x</ci>

</bvar>

<apply>

<root/>

<apply>

<power/>

<ci>x</ci>

<cn>-1</cn>

</apply>

</apply>

</apply>

>>>mathml(Integral(sqrt(1/x),x))

'<apply><int/><bvar><ci>x</ci></bvar><apply><root/><apply><power/><ci>x</ci><cn>-1</cn></apply></apply></apply>'