AI พร้อม Python - การเรียนรู้ภายใต้การดูแล: การจำแนกประเภท
ในบทนี้เราจะมุ่งเน้นไปที่การใช้การเรียนรู้ภายใต้การดูแล - การจำแนกประเภท
เทคนิคการจำแนกประเภทหรือแบบจำลองพยายามหาข้อสรุปจากค่าที่สังเกตได้ ในปัญหาการจัดหมวดหมู่เรามีผลลัพธ์ที่จัดหมวดหมู่เช่น“ ดำ” หรือ“ ขาว” หรือ“ การสอน” และ“ ไม่ใช่การสอน” ในขณะที่สร้างโมเดลการจำแนกเราจำเป็นต้องมีชุดข้อมูลการฝึกอบรมที่มีจุดข้อมูลและป้ายกำกับที่เกี่ยวข้อง ตัวอย่างเช่นหากเราต้องการตรวจสอบว่าภาพนั้นเป็นของรถยนต์หรือไม่ สำหรับการตรวจสอบสิ่งนี้เราจะสร้างชุดข้อมูลการฝึกอบรมโดยมีสองคลาสที่เกี่ยวข้องกับ "รถ" และ "ไม่มีรถ" จากนั้นเราต้องฝึกโมเดลโดยใช้ตัวอย่างการฝึกอบรม รูปแบบการจำแนกประเภทส่วนใหญ่จะใช้ในการจดจำใบหน้าการระบุสแปมและอื่น ๆ
ขั้นตอนในการสร้างลักษณนามใน Python
สำหรับการสร้างลักษณนามใน Python เราจะใช้ Python 3 และ Scikit-learn ซึ่งเป็นเครื่องมือสำหรับการเรียนรู้ของเครื่อง ทำตามขั้นตอนเหล่านี้เพื่อสร้างลักษณนามใน Python -
ขั้นตอนที่ 1 - นำเข้า Scikit-learn
นี่เป็นขั้นตอนแรกสำหรับการสร้างลักษณนามใน Python ในขั้นตอนนี้เราจะติดตั้งแพ็คเกจ Python ที่เรียกว่า Scikit-learn ซึ่งเป็นหนึ่งในโมดูลการเรียนรู้ของเครื่องที่ดีที่สุดใน Python คำสั่งต่อไปนี้จะช่วยเรานำเข้าแพ็คเกจ -
Import Sklearnขั้นตอนที่ 2 - นำเข้าชุดข้อมูลของ Scikit-learn
ในขั้นตอนนี้เราสามารถเริ่มทำงานกับชุดข้อมูลสำหรับโมเดลแมชชีนเลิร์นนิงของเราได้ ที่นี่เราจะใช้the ฐานข้อมูลการวินิจฉัยมะเร็งเต้านมวิสคอนซิน ชุดข้อมูลประกอบด้วยข้อมูลต่างๆเกี่ยวกับเนื้องอกมะเร็งเต้านมและฉลากการจำแนกประเภทของmalignant หรือ benign. ชุดข้อมูลมี 569 อินสแตนซ์หรือข้อมูลเกี่ยวกับเนื้องอก 569 ชิ้นและมีข้อมูลเกี่ยวกับคุณลักษณะหรือคุณลักษณะ 30 อย่างเช่นรัศมีของเนื้องอกพื้นผิวความเรียบเนียนและพื้นที่ ด้วยความช่วยเหลือของคำสั่งต่อไปนี้เราสามารถนำเข้าชุดข้อมูลมะเร็งเต้านมของ Scikit-learn -
from sklearn.datasets import load_breast_cancerตอนนี้คำสั่งต่อไปนี้จะโหลดชุดข้อมูล
data = load_breast_cancer()ต่อไปนี้เป็นรายการคีย์พจนานุกรมที่สำคัญ -
- ชื่อป้ายกำกับการจำแนก (target_names)
- ป้ายกำกับจริง (เป้าหมาย)
- ชื่อแอตทริบิวต์ / คุณลักษณะ (feature_names)
- แอตทริบิวต์ (ข้อมูล)
ตอนนี้ด้วยความช่วยเหลือของคำสั่งต่อไปนี้เราสามารถสร้างตัวแปรใหม่สำหรับชุดข้อมูลที่สำคัญแต่ละชุดและกำหนดข้อมูลได้ กล่าวอีกนัยหนึ่งเราสามารถจัดระเบียบข้อมูลด้วยคำสั่งต่อไปนี้ -
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']ตอนนี้เพื่อให้ชัดเจนขึ้นเราสามารถพิมพ์ฉลากคลาสฉลากของอินสแตนซ์ข้อมูลแรกชื่อคุณลักษณะและค่าของคุณลักษณะได้ด้วยความช่วยเหลือของคำสั่งต่อไปนี้ -
print(label_names)คำสั่งดังกล่าวจะพิมพ์ชื่อคลาสที่ร้ายกาจและอ่อนโยนตามลำดับ แสดงเป็นผลลัพธ์ด้านล่าง -
['malignant' 'benign']ตอนนี้คำสั่งด้านล่างจะแสดงว่ามีการแมปกับค่าไบนารี 0 และ 1 ในที่นี้ 0 หมายถึงมะเร็งร้ายและ 1 หมายถึงมะเร็งที่อ่อนโยน คุณจะได้รับผลลัพธ์ต่อไปนี้ -
print(labels[0])
0คำสั่งสองคำสั่งด้านล่างนี้จะสร้างชื่อคุณลักษณะและค่าคุณลักษณะ
print(feature_names[0])
mean radius
print(features[0])
[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03
1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01
2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01
8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02
5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03
2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03
1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01
4.60100000e-01 1.18900000e-01]จากผลลัพธ์ข้างต้นเราจะเห็นว่าอินสแตนซ์ข้อมูลแรกเป็นเนื้องอกมะเร็งซึ่งมีรัศมี 1.7990000e + 01
ขั้นตอนที่ 3 - จัดระเบียบข้อมูลเป็นชุด
ในขั้นตอนนี้เราจะแบ่งข้อมูลของเราออกเป็นสองส่วนคือชุดฝึกและชุดทดสอบ การแบ่งข้อมูลออกเป็นชุดเหล่านี้มีความสำคัญมากเพราะเราต้องทดสอบโมเดลของเรากับข้อมูลที่มองไม่เห็น ในการแบ่งข้อมูลออกเป็นชุด sklearn มีฟังก์ชันที่เรียกว่าtrain_test_split()ฟังก์ชัน ด้วยความช่วยเหลือของคำสั่งต่อไปนี้เราสามารถแบ่งข้อมูลในชุดเหล่านี้ -
from sklearn.model_selection import train_test_splitคำสั่งดังกล่าวจะนำเข้าไฟล์ train_test_splitฟังก์ชั่นจาก sklearn และคำสั่งด้านล่างจะแบ่งข้อมูลออกเป็นข้อมูลการฝึกอบรมและการทดสอบ ในตัวอย่างด้านล่างนี้เรากำลังใช้ข้อมูล 40% สำหรับการทดสอบและข้อมูลที่เหลือจะใช้สำหรับการฝึกโมเดล
train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)ขั้นตอนที่ 4 - การสร้างแบบจำลอง
ในขั้นตอนนี้เราจะสร้างแบบจำลองของเรา เราจะใช้อัลกอริทึมNaïve Bayes ในการสร้างแบบจำลอง คำสั่งต่อไปนี้สามารถใช้เพื่อสร้างแบบจำลอง -
from sklearn.naive_bayes import GaussianNBคำสั่งดังกล่าวจะนำเข้าโมดูล GaussianNB ตอนนี้คำสั่งต่อไปนี้จะช่วยคุณเริ่มต้นโมเดล
gnb = GaussianNB()เราจะฝึกโมเดลโดยปรับให้พอดีกับข้อมูลโดยใช้ gnb.fit ()
model = gnb.fit(train, train_labels)ขั้นตอนที่ 5 - การประเมินโมเดลและความแม่นยำ
ในขั้นตอนนี้เราจะประเมินแบบจำลองโดยทำการคาดคะเนข้อมูลการทดสอบของเรา จากนั้นเราจะพบความแม่นยำของมันด้วย สำหรับการคาดคะเนเราจะใช้ฟังก์ชัน Predict () คำสั่งต่อไปนี้จะช่วยคุณทำสิ่งนี้ -
preds = gnb.predict(test)
print(preds)
[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1
0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0
0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0
0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0
1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0
1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0
1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0
1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]ชุด 0 และ 1 ข้างต้นเป็นค่าที่คาดการณ์ไว้สำหรับชั้นเนื้องอก - ร้ายและไม่เป็นพิษเป็นภัย
ตอนนี้โดยการเปรียบเทียบสองอาร์เรย์คือ test_labels และ predsเราสามารถค้นหาความแม่นยำของแบบจำลองของเราได้ เราจะใช้ไฟล์accuracy_score()ฟังก์ชันเพื่อกำหนดความถูกต้อง พิจารณาคำสั่งต่อไปนี้สำหรับสิ่งนี้ -
from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965ผลลัพธ์แสดงให้เห็นว่าลักษณนามNaïveBayesมีความแม่นยำ 95.17%
ด้วยวิธีนี้ด้วยความช่วยเหลือของขั้นตอนข้างต้นเราสามารถสร้างลักษณนามของเราใน Python
Building Classifier ใน Python
ในส่วนนี้เราจะเรียนรู้วิธีการสร้างลักษณนามใน Python
ลักษณนามNaïve Bayes
Naïve Bayes เป็นเทคนิคการจำแนกประเภทที่ใช้ในการสร้างลักษณนามโดยใช้ทฤษฎีบทเบย์ สมมติฐานคือตัวทำนายมีความเป็นอิสระ กล่าวง่ายๆก็คือถือว่าการมีอยู่ของคุณลักษณะเฉพาะในชั้นเรียนนั้นไม่เกี่ยวข้องกับการมีอยู่ของคุณลักษณะอื่นใด สำหรับการสร้างลักษณนามNaïve Bayes เราจำเป็นต้องใช้ python library ที่เรียกว่า scikit learn โมเดลNaïve Bayes มีสามประเภทGaussian, Multinomial and Bernoulli ภายใต้แพ็คเกจการเรียนรู้ scikit
ในการสร้างโมเดลลักษณนามการเรียนรู้ของเครื่องNaïve Bayes เราจำเป็นต้องมีสิ่งต่อไปนี้ & ลบ
ชุดข้อมูล
เราจะใช้ชุดข้อมูลที่ชื่อว่าBreast Cancer Wisconsin Diagnostic Database ชุดข้อมูลประกอบด้วยข้อมูลต่างๆเกี่ยวกับเนื้องอกมะเร็งเต้านมและฉลากการจำแนกประเภทของmalignant หรือ benign. ชุดข้อมูลมี 569 อินสแตนซ์หรือข้อมูลเกี่ยวกับเนื้องอก 569 ชิ้นและมีข้อมูลเกี่ยวกับคุณลักษณะหรือคุณลักษณะ 30 อย่างเช่นรัศมีของเนื้องอกพื้นผิวความเรียบเนียนและพื้นที่ เราสามารถนำเข้าชุดข้อมูลนี้จากแพ็คเกจ sklearn
Naïve Bayes Model
สำหรับการสร้างลักษณนามNaïve Bayes เราต้องการแบบจำลองNaïve Bayes อย่างที่บอกไปก่อนหน้านี้มีชื่อรุ่นNaïve Bayes อยู่สามประเภทGaussian, Multinomial และ Bernoulliภายใต้แพ็คเกจการเรียนรู้ scikit ในตัวอย่างต่อไปนี้เราจะใช้แบบจำลอง Gaussian Naïve Bayes
ด้วยการใช้ข้างต้นเราจะสร้างแบบจำลองการเรียนรู้ของเครื่อง Na useve Bayes เพื่อใช้ข้อมูลเนื้องอกในการทำนายว่าเนื้องอกเป็นมะเร็งหรือไม่เป็นพิษหรือไม่
ในการเริ่มต้นเราต้องติดตั้งโมดูล sklearn สามารถทำได้ด้วยความช่วยเหลือของคำสั่งต่อไปนี้ -
Import Sklearnตอนนี้เราต้องนำเข้าชุดข้อมูลที่ชื่อว่า Breast Cancer Wisconsin Diagnostic Database
from sklearn.datasets import load_breast_cancerตอนนี้คำสั่งต่อไปนี้จะโหลดชุดข้อมูล
data = load_breast_cancer()สามารถจัดระเบียบข้อมูลได้ดังนี้ -
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']ตอนนี้เพื่อให้ชัดเจนยิ่งขึ้นเราสามารถพิมพ์ฉลากคลาสฉลากของอินสแตนซ์ข้อมูลแรกชื่อคุณลักษณะและค่าของคุณลักษณะด้วยความช่วยเหลือของคำสั่งต่อไปนี้ -
print(label_names)คำสั่งดังกล่าวจะพิมพ์ชื่อคลาสที่ร้ายกาจและอ่อนโยนตามลำดับ แสดงเป็นผลลัพธ์ด้านล่าง -
['malignant' 'benign']ตอนนี้คำสั่งที่ระบุด้านล่างจะแสดงว่ามีการแมปกับค่าไบนารี 0 และ 1 ในที่นี้ 0 หมายถึงมะเร็งร้ายและ 1 หมายถึงมะเร็งที่อ่อนโยน แสดงเป็นผลลัพธ์ด้านล่าง -
print(labels[0])
0คำสั่งสองคำสั่งต่อไปนี้จะสร้างชื่อคุณลักษณะและค่าคุณลักษณะ
print(feature_names[0])
mean radius
print(features[0])
[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03
1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01
2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01
8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02
5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03
2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03
1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01
4.60100000e-01 1.18900000e-01]จากผลลัพธ์ข้างต้นเราจะเห็นว่าอินสแตนซ์ข้อมูลแรกเป็นเนื้องอกมะเร็งซึ่งรัศมีหลักคือ 1.7990000e + 01
สำหรับการทดสอบโมเดลของเรากับข้อมูลที่มองไม่เห็นเราจำเป็นต้องแยกข้อมูลของเราออกเป็นข้อมูลการฝึกอบรมและการทดสอบ สามารถทำได้ด้วยความช่วยเหลือของรหัสต่อไปนี้ -
from sklearn.model_selection import train_test_splitคำสั่งดังกล่าวจะนำเข้าไฟล์ train_test_splitฟังก์ชั่นจาก sklearn และคำสั่งด้านล่างจะแบ่งข้อมูลออกเป็นข้อมูลการฝึกอบรมและการทดสอบ ในตัวอย่างด้านล่างเราใช้ 40% ของข้อมูลสำหรับการทดสอบและข้อมูลการปรับปรุงจะถูกใช้สำหรับการฝึกโมเดล
train, test, train_labels, test_labels =
train_test_split(features,labels,test_size = 0.40, random_state = 42)ตอนนี้เรากำลังสร้างโมเดลด้วยคำสั่งต่อไปนี้ -
from sklearn.naive_bayes import GaussianNBคำสั่งดังกล่าวจะนำเข้าไฟล์ GaussianNBโมดูล. ตอนนี้ด้วยคำสั่งที่ระบุด้านล่างเราจำเป็นต้องเริ่มต้นโมเดล
gnb = GaussianNB()เราจะฝึกโมเดลโดยปรับให้พอดีกับข้อมูลโดยใช้ gnb.fit().
model = gnb.fit(train, train_labels)ตอนนี้ประเมินแบบจำลองโดยทำการคาดคะเนข้อมูลทดสอบและสามารถทำได้ดังนี้ -
preds = gnb.predict(test)
print(preds)
[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1
0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0
0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0
0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0
1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0
1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0
1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0
1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]ชุด 0 และ 1 ข้างต้นเป็นค่าที่คาดการณ์ไว้สำหรับชั้นเนื้องอกเช่นมะเร็งและไม่เป็นพิษเป็นภัย
ตอนนี้โดยการเปรียบเทียบสองอาร์เรย์คือ test_labels และ predsเราสามารถค้นหาความแม่นยำของแบบจำลองของเราได้ เราจะใช้ไฟล์accuracy_score()ฟังก์ชันเพื่อกำหนดความถูกต้อง พิจารณาคำสั่งต่อไปนี้ -
from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965ผลลัพธ์แสดงให้เห็นว่าลักษณนามNaïveBayesมีความแม่นยำ 95.17%
นั่นคือลักษณนามแมชชีนเลิร์นนิงตามแบบจำลองNaïve Bayse Gaussian
รองรับ Vector Machines (SVM)
โดยทั่วไป Support vector machine (SVM) เป็นอัลกอริธึมการเรียนรู้ของเครื่องที่อยู่ภายใต้การดูแลซึ่งสามารถใช้ได้ทั้งการถดถอยและการจำแนกประเภท แนวคิดหลักของ SVM คือการพล็อตรายการข้อมูลแต่ละรายการเป็นจุดในปริภูมิ n มิติโดยค่าของแต่ละคุณลักษณะเป็นค่าของพิกัดเฉพาะ นี่คือคุณสมบัติที่เราจะมี ต่อไปนี้เป็นการแสดงภาพกราฟิกอย่างง่ายเพื่อให้เข้าใจแนวคิดของ SVM -
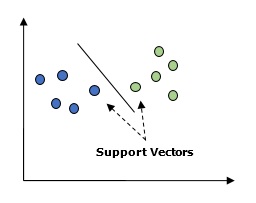
ในแผนภาพด้านบนเรามีคุณสมบัติสองประการ ดังนั้นก่อนอื่นเราต้องพล็อตตัวแปรทั้งสองนี้ในพื้นที่สองมิติโดยแต่ละจุดมีสองพิกัดเรียกว่าเวกเตอร์สนับสนุน เส้นแบ่งข้อมูลออกเป็นสองกลุ่มที่แตกต่างกัน บรรทัดนี้จะเป็นลักษณนาม
ที่นี่เราจะสร้างตัวจำแนก SVM โดยใช้ชุดข้อมูล scikit-learn และ iris ห้องสมุด Scikitlearn มีไฟล์sklearn.svmโมดูลและจัดเตรียม sklearn.svm.svc สำหรับการจำแนกประเภท ลักษณนาม SVM เพื่อทำนายคลาสของพืชไอริสตามคุณสมบัติ 4 ประการดังแสดงด้านล่าง
ชุดข้อมูล
เราจะใช้ชุดข้อมูลไอริสซึ่งมี 3 คลาสละ 50 อินสแตนซ์โดยแต่ละคลาสหมายถึงพืชไอริสชนิดหนึ่ง แต่ละอินสแตนซ์มีคุณสมบัติสี่ประการ ได้แก่ ความยาวกลีบเลี้ยงความกว้างของกลีบเลี้ยงความยาวกลีบดอกและความกว้างของกลีบดอก ลักษณนาม SVM เพื่อทำนายคลาสของพืชไอริสตามคุณสมบัติ 4 ประการดังแสดงด้านล่าง
เคอร์เนล
เป็นเทคนิคที่ SVM ใช้ โดยพื้นฐานแล้วสิ่งเหล่านี้เป็นฟังก์ชันที่ใช้พื้นที่อินพุตมิติต่ำและเปลี่ยนเป็นพื้นที่มิติที่สูงขึ้น จะแปลงปัญหาที่ไม่สามารถแยกออกเป็นปัญหาที่แยกออกจากกันได้ ฟังก์ชันเคอร์เนลสามารถเป็นฟังก์ชันใดก็ได้ระหว่าง linear, polynomial, rbf และ sigmoid ในตัวอย่างนี้เราจะใช้เคอร์เนลเชิงเส้น
ให้เรานำเข้าแพ็คเกจต่อไปนี้ -
import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as pltตอนนี้โหลดข้อมูลอินพุต -
iris = datasets.load_iris()เรากำลังใช้คุณสมบัติสองประการแรก -
X = iris.data[:, :2]
y = iris.targetเราจะพล็อตขอบเขตเครื่องเวกเตอร์สนับสนุนด้วยข้อมูลต้นฉบับ เรากำลังสร้างตาข่ายเพื่อลงจุด
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]เราจำเป็นต้องให้ค่าของพารามิเตอร์การทำให้เป็นมาตรฐาน
C = 1.0เราจำเป็นต้องสร้างวัตถุลักษณนาม SVM
Svc_classifier = svm_classifier.SVC(kernel='linear',
C=C, decision_function_shape = 'ovr').fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize = (15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap = plt.cm.tab10, alpha = 0.3)
plt.scatter(X[:, 0], X[:, 1], c = y, cmap = plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('SVC with linear kernel')
การถดถอยโลจิสติก
โดยพื้นฐานแล้วแบบจำลองการถดถอยโลจิสติกเป็นหนึ่งในสมาชิกของตระกูลอัลกอริธึมการจำแนกประเภทภายใต้การดูแล การถดถอยโลจิสติกจะวัดความสัมพันธ์ระหว่างตัวแปรตามและตัวแปรอิสระโดยการประมาณความน่าจะเป็นโดยใช้ฟังก์ชันโลจิสติกส์
ที่นี่ถ้าเราพูดถึงตัวแปรตามและตัวแปรอิสระตัวแปรตามคือตัวแปรคลาสเป้าหมายที่เราจะทำนายและในอีกด้านหนึ่งตัวแปรอิสระคือคุณสมบัติที่เราจะใช้ในการทำนายคลาสเป้าหมาย
ในการถดถอยโลจิสติกการประมาณความน่าจะเป็นหมายถึงการทำนายโอกาสที่จะเกิดเหตุการณ์ ตัวอย่างเช่นเจ้าของร้านต้องการทำนายว่าลูกค้าที่เข้ามาในร้านจะซื้อ play station (เป็นต้น) หรือไม่ จะมีคุณสมบัติหลายอย่างของลูกค้า - เพศอายุ ฯลฯ ซึ่งจะสังเกตได้จากผู้ดูแลร้านเพื่อทำนายความเป็นไปได้ที่จะเกิดขึ้นเช่นซื้อเครื่องเล่นหรือไม่ ฟังก์ชันโลจิสติกคือเส้นโค้งซิกมอยด์ที่ใช้ในการสร้างฟังก์ชันด้วยพารามิเตอร์ต่างๆ
ข้อกำหนดเบื้องต้น
ก่อนสร้างลักษณนามโดยใช้การถดถอยโลจิสติกส์เราจำเป็นต้องติดตั้งแพ็คเกจ Tkinter ในระบบของเรา สามารถติดตั้งได้จากhttps://docs.python.org/2/library/tkinter.html.
ตอนนี้ด้วยความช่วยเหลือของรหัสที่ระบุด้านล่างเราสามารถสร้างลักษณนามโดยใช้การถดถอยโลจิสติก -
ขั้นแรกเราจะนำเข้าบางแพ็คเกจ -
import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as pltตอนนี้เราต้องกำหนดข้อมูลตัวอย่างซึ่งสามารถทำได้ดังนี้ -
X = np.array([[2, 4.8], [2.9, 4.7], [2.5, 5], [3.2, 5.5], [6, 5], [7.6, 4],
[3.2, 0.9], [2.9, 1.9],[2.4, 3.5], [0.5, 3.4], [1, 4], [0.9, 5.9]])
y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3])ต่อไปเราต้องสร้างลักษณนามการถดถอยโลจิสติกซึ่งสามารถทำได้ดังนี้ -
Classifier_LR = linear_model.LogisticRegression(solver = 'liblinear', C = 75)สุดท้าย แต่ไม่ท้ายสุดเราต้องฝึกลักษณนามนี้ -
Classifier_LR.fit(X, y)ทีนี้เราจะเห็นภาพผลลัพธ์ได้อย่างไร? สามารถทำได้โดยสร้างฟังก์ชันชื่อ Logistic_visualize () -
Def Logistic_visualize(Classifier_LR, X, y):
min_x, max_x = X[:, 0].min() - 1.0, X[:, 0].max() + 1.0
min_y, max_y = X[:, 1].min() - 1.0, X[:, 1].max() + 1.0ในบรรทัดด้านบนเรากำหนดค่าต่ำสุดและสูงสุด X และ Y ที่จะใช้ในตารางตาข่าย นอกจากนี้เราจะกำหนดขนาดขั้นตอนสำหรับการลงจุดตารางตาข่าย
mesh_step_size = 0.02ให้เรากำหนดตารางตาข่ายของค่า X และ Y ดังนี้ -
x_vals, y_vals = np.meshgrid(np.arange(min_x, max_x, mesh_step_size),
np.arange(min_y, max_y, mesh_step_size))ด้วยความช่วยเหลือของรหัสต่อไปนี้เราสามารถเรียกใช้ลักษณนามบนตารางตาข่าย -
output = classifier.predict(np.c_[x_vals.ravel(), y_vals.ravel()])
output = output.reshape(x_vals.shape)
plt.figure()
plt.pcolormesh(x_vals, y_vals, output, cmap = plt.cm.gray)
plt.scatter(X[:, 0], X[:, 1], c = y, s = 75, edgecolors = 'black',
linewidth=1, cmap = plt.cm.Paired)โค้ดบรรทัดต่อไปนี้จะระบุขอบเขตของพล็อต
plt.xlim(x_vals.min(), x_vals.max())
plt.ylim(y_vals.min(), y_vals.max())
plt.xticks((np.arange(int(X[:, 0].min() - 1), int(X[:, 0].max() + 1), 1.0)))
plt.yticks((np.arange(int(X[:, 1].min() - 1), int(X[:, 1].max() + 1), 1.0)))
plt.show()ตอนนี้หลังจากรันโค้ดแล้วเราจะได้ผลลัพธ์ต่อไปนี้ลักษณนามการถดถอยโลจิสติกส์ -

ลักษณนามทรีการตัดสินใจ
แผนผังการตัดสินใจเป็นผังงานต้นไม้ไบนารีที่แต่ละโหนดแยกกลุ่มการสังเกตตามตัวแปรคุณลักษณะบางอย่าง
ที่นี่เรากำลังสร้างลักษณนาม Decision Tree สำหรับทำนายเพศชายหรือเพศหญิง เราจะใช้ชุดข้อมูลขนาดเล็กมากซึ่งมี 19 ตัวอย่าง ตัวอย่างเหล่านี้จะประกอบด้วยคุณสมบัติสองประการ - "ความสูง" และ "ความยาวของผม"
ข้อกำหนดเบื้องต้น
สำหรับการสร้างลักษณนามต่อไปนี้เราจำเป็นต้องติดตั้ง pydotplus และ graphviz. โดยทั่วไป graphviz เป็นเครื่องมือสำหรับการวาดภาพกราฟิกโดยใช้ไฟล์ dot และpydotplusเป็นโมดูลสำหรับภาษา Dot ของ Graphviz สามารถติดตั้งด้วยตัวจัดการแพ็คเกจหรือ pip
ตอนนี้เราสามารถสร้างลักษณนามทรีการตัดสินใจโดยใช้รหัส Python ต่อไปนี้ -
เริ่มต้นด้วยการให้เรานำเข้าไลบรารีที่สำคัญบางส่วนดังนี้ -
import pydotplus
from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.metrics import classification_report
from sklearn import cross_validation
import collectionsตอนนี้เราต้องจัดเตรียมชุดข้อมูลดังนี้ -
X = [[165,19],[175,32],[136,35],[174,65],[141,28],[176,15],[131,32],
[166,6],[128,32],[179,10],[136,34],[186,2],[126,25],[176,28],[112,38],
[169,9],[171,36],[116,25],[196,25]]
Y = ['Man','Woman','Woman','Man','Woman','Man','Woman','Man','Woman',
'Man','Woman','Man','Woman','Woman','Woman','Man','Woman','Woman','Man']
data_feature_names = ['height','length of hair']
X_train, X_test, Y_train, Y_test = cross_validation.train_test_split
(X, Y, test_size=0.40, random_state=5)หลังจากจัดเตรียมชุดข้อมูลแล้วเราจำเป็นต้องใส่แบบจำลองซึ่งสามารถทำได้ดังนี้ -
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X,Y)การทำนายสามารถทำได้ด้วยความช่วยเหลือของรหัส Python ต่อไปนี้ -
prediction = clf.predict([[133,37]])
print(prediction)เราสามารถเห็นภาพแผนผังการตัดสินใจด้วยความช่วยเหลือของรหัส Python ต่อไปนี้ -
dot_data = tree.export_graphviz(clf,feature_names = data_feature_names,
out_file = None,filled = True,rounded = True)
graph = pydotplus.graph_from_dot_data(dot_data)
colors = ('orange', 'yellow')
edges = collections.defaultdict(list)
for edge in graph.get_edge_list():
edges[edge.get_source()].append(int(edge.get_destination()))
for edge in edges: edges[edge].sort()
for i in range(2):dest = graph.get_node(str(edges[edge][i]))[0]
dest.set_fillcolor(colors[i])
graph.write_png('Decisiontree16.png')มันจะให้การคาดการณ์สำหรับรหัสข้างต้นเป็น [‘Woman’] และสร้างแผนผังการตัดสินใจต่อไปนี้ -

เราสามารถเปลี่ยนค่าของคุณสมบัติในการทำนายเพื่อทดสอบได้
ลักษณนามป่าสุ่ม
อย่างที่เราทราบกันดีว่าวิธีการทั้งมวลเป็นวิธีการที่รวมโมเดลการเรียนรู้ของเครื่องเข้ากับโมเดลการเรียนรู้ของเครื่องที่มีประสิทธิภาพมากขึ้น Random Forest ซึ่งเป็นกลุ่มของต้นไม้แห่งการตัดสินใจเป็นหนึ่งในนั้น จะดีกว่าโครงสร้างการตัดสินใจเพียงครั้งเดียวเนื่องจากในขณะที่ยังคงรักษาอำนาจในการทำนายไว้ก็สามารถลดความเหมาะสมมากเกินไปโดยการหาค่าเฉลี่ยของผลลัพธ์ ที่นี่เราจะนำแบบจำลองฟอเรสต์สุ่มไปใช้กับชุดข้อมูลการเรียนรู้มะเร็งของ scikit
นำเข้าแพ็คเกจที่จำเป็น -
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
import matplotlib.pyplot as plt
import numpy as npตอนนี้เราต้องจัดเตรียมชุดข้อมูลซึ่งสามารถทำได้ดังนี้ & ลบ
cancer = load_breast_cancer()
X_train, X_test, y_train,
y_test = train_test_split(cancer.data, cancer.target, random_state = 0)หลังจากจัดเตรียมชุดข้อมูลแล้วเราจำเป็นต้องใส่แบบจำลองซึ่งสามารถทำได้ดังนี้ -
forest = RandomForestClassifier(n_estimators = 50, random_state = 0)
forest.fit(X_train,y_train)ตอนนี้รับความแม่นยำในการฝึกอบรมและชุดย่อยการทดสอบ: ถ้าเราจะเพิ่มจำนวนตัวประมาณค่าความแม่นยำของชุดทดสอบก็จะเพิ่มขึ้นด้วย
print('Accuracy on the training subset:(:.3f)',format(forest.score(X_train,y_train)))
print('Accuracy on the training subset:(:.3f)',format(forest.score(X_test,y_test)))เอาต์พุต
Accuracy on the training subset:(:.3f) 1.0
Accuracy on the training subset:(:.3f) 0.965034965034965ตอนนี้เช่นเดียวกับต้นไม้ตัดสินใจป่าสุ่มมี feature_importanceโมดูลซึ่งจะให้มุมมองของน้ำหนักคุณลักษณะได้ดีกว่าโครงสร้างการตัดสินใจ สามารถพล็อตและเห็นภาพได้ดังนี้ -
n_features = cancer.data.shape[1]
plt.barh(range(n_features),forest.feature_importances_, align='center')
plt.yticks(np.arange(n_features),cancer.feature_names)
plt.xlabel('Feature Importance')
plt.ylabel('Feature')
plt.show()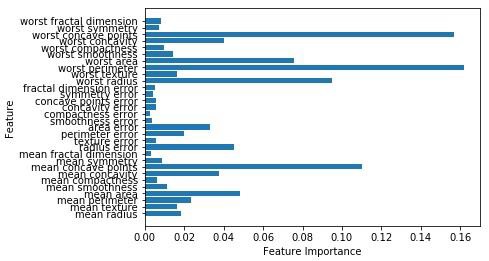
ประสิทธิภาพของลักษณนาม
หลังจากใช้อัลกอริธึมแมชชีนเลิร์นนิงแล้วเราจำเป็นต้องค้นหาว่าโมเดลมีประสิทธิภาพเพียงใด เกณฑ์ในการวัดประสิทธิภาพอาจขึ้นอยู่กับชุดข้อมูลและเมตริก สำหรับการประเมินอัลกอริทึมการเรียนรู้ของเครื่องต่างๆเราสามารถใช้เมตริกประสิทธิภาพที่แตกต่างกันได้ ตัวอย่างเช่นสมมติว่าหากมีการใช้ลักษณนามเพื่อแยกความแตกต่างระหว่างรูปภาพของวัตถุต่างๆเราสามารถใช้เมตริกประสิทธิภาพการจำแนกประเภทเช่นความแม่นยำเฉลี่ย AUC เป็นต้นหรือในอีกแง่หนึ่งเมตริกที่เราเลือกเพื่อประเมินโมเดลการเรียนรู้ของเครื่องคือ สำคัญมากเนื่องจากการเลือกเมตริกมีผลต่อการวัดและเปรียบเทียบประสิทธิภาพของอัลกอริทึมการเรียนรู้ของเครื่อง ต่อไปนี้เป็นเมตริกบางส่วน -
เมทริกซ์ความสับสน
โดยทั่วไปจะใช้สำหรับปัญหาการจำแนกประเภทที่เอาต์พุตสามารถเป็นคลาสสองประเภทขึ้นไป เป็นวิธีที่ง่ายที่สุดในการวัดประสิทธิภาพของลักษณนาม เมทริกซ์ความสับสนโดยพื้นฐานแล้วเป็นตารางที่มีสองมิติคือ "ตามจริง" และ "คาดการณ์" มิติข้อมูลทั้งสองมี“ True Positives (TP)”,“ True Negatives (TN)”,“ False Positives (FP)”,“ False Negatives (FN)”
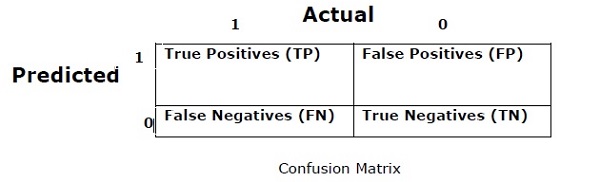
ในเมทริกซ์ความสับสนด้านบน 1 คือคลาสบวกและ 0 สำหรับคลาสลบ
ต่อไปนี้เป็นคำศัพท์ที่เกี่ยวข้องกับ Confusion matrix -
True Positives − TPs คือกรณีที่คลาสจริงของจุดข้อมูลคือ 1 และการคาดการณ์ก็คือ 1 เช่นกัน
True Negatives − TN เป็นกรณีที่คลาสจริงของจุดข้อมูลเป็น 0 และการทำนายเป็น 0 ด้วย
False Positives − FPs คือกรณีที่คลาสจริงของจุดข้อมูลคือ 0 และการคาดการณ์ก็เป็น 1 เช่นกัน
False Negatives − FN เป็นกรณีที่คลาสจริงของจุดข้อมูลคือ 1 และการคาดการณ์เป็น 0 เช่นกัน
ความถูกต้อง
เมทริกซ์ความสับสนนั้นไม่ได้เป็นตัววัดประสิทธิภาพ แต่เมทริกซ์ประสิทธิภาพเกือบทั้งหมดจะขึ้นอยู่กับเมทริกซ์ความสับสน หนึ่งในนั้นคือความถูกต้อง ในปัญหาการจัดหมวดหมู่อาจกำหนดเป็นจำนวนการคาดการณ์ที่ถูกต้องที่สร้างขึ้นโดยตัวแบบมากกว่าการคาดคะเนทุกประเภท สูตรการคำนวณความแม่นยำมีดังนี้ -
$$ ความแม่นยำ = \ frac {TP + TN} {TP + FP + FN + TN} $$
ความแม่นยำ
ส่วนใหญ่จะใช้ในการดึงเอกสาร อาจกำหนดเป็นจำนวนเอกสารที่ส่งคืนถูกต้อง ต่อไปนี้เป็นสูตรคำนวณความแม่นยำ -
$$ Precision = \ frac {TP} {TP + FP} $$
การเรียกคืนหรือความอ่อนไหว
อาจกำหนดเป็นจำนวนผลบวกที่โมเดลส่งกลับมา ต่อไปนี้เป็นสูตรคำนวณการเรียกคืน / ความไวของแบบจำลอง -
$$ Recall = \ frac {TP} {TP + FN} $$
ความจำเพาะ
อาจกำหนดเป็นจำนวนเชิงลบที่โมเดลส่งคืน มันตรงข้ามกับการจำ ต่อไปนี้เป็นสูตรคำนวณความจำเพาะของแบบจำลอง -
$$ ความจำเพาะ = \ frac {TN} {TN + FP} $$
ปัญหาความไม่สมดุลของคลาส
ความไม่สมดุลของคลาสคือสถานการณ์ที่จำนวนการสังเกตของคลาสหนึ่งต่ำกว่าคลาสอื่นอย่างมีนัยสำคัญ ตัวอย่างเช่นปัญหานี้มีความโดดเด่นในสถานการณ์ที่เราจำเป็นต้องระบุโรคที่หายากธุรกรรมฉ้อโกงในธนาคารเป็นต้น
ตัวอย่างคลาสที่ไม่สมดุล
ให้เราพิจารณาตัวอย่างของชุดข้อมูลการตรวจจับการฉ้อโกงเพื่อทำความเข้าใจแนวคิดของคลาสที่ไม่สมดุล -
Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%วิธีการแก้
Balancing the classes’ทำหน้าที่เป็นวิธีแก้ปัญหาสำหรับชั้นเรียนที่ไม่สมดุล วัตถุประสงค์หลักของการปรับสมดุลของคลาสคือการเพิ่มความถี่ของคลาสของชนกลุ่มน้อยหรือลดความถี่ของคลาสส่วนใหญ่ ต่อไปนี้เป็นแนวทางในการแก้ปัญหาความไม่สมดุลของคลาส -
การสุ่มตัวอย่างซ้ำ
การสุ่มตัวอย่างซ้ำเป็นชุดวิธีการที่ใช้ในการสร้างชุดข้อมูลตัวอย่างขึ้นใหม่ทั้งชุดฝึกและชุดทดสอบ ทำการสุ่มตัวอย่างซ้ำเพื่อปรับปรุงความแม่นยำของแบบจำลอง ต่อไปนี้เป็นเทคนิคการสุ่มตัวอย่างซ้ำบางส่วน -
Random Under-Sampling- เทคนิคนี้มีจุดมุ่งหมายเพื่อสร้างสมดุลของการกระจายชั้นเรียนโดยการสุ่มกำจัดตัวอย่างชั้นเรียนส่วนใหญ่ สิ่งนี้จะทำจนกว่าอินสแตนซ์คลาสส่วนใหญ่และคลาสส่วนน้อยจะสมดุลกัน
Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%ในกรณีนี้เราจะนำตัวอย่าง 10% โดยไม่มีการเปลี่ยนจากอินสแตนซ์ที่ไม่ใช่การฉ้อโกงแล้วรวมเข้ากับอินสแตนซ์การฉ้อโกง -
การสังเกตที่ไม่เป็นการฉ้อโกงหลังจากการสุ่มภายใต้การสุ่มตัวอย่าง = 10% ของ 4950 = 495
การสังเกตการณ์ทั้งหมดหลังจากรวมเข้ากับการสังเกตการณ์หลอกลวง = 50 + 495 = 545
ดังนั้นตอนนี้อัตราเหตุการณ์สำหรับชุดข้อมูลใหม่หลังจากอยู่ภายใต้การสุ่มตัวอย่าง = 9%
ข้อได้เปรียบหลักของเทคนิคนี้คือสามารถลดเวลาในการทำงานและปรับปรุงการจัดเก็บ แต่ในอีกด้านหนึ่งก็สามารถทิ้งข้อมูลที่เป็นประโยชน์ในขณะที่ลดจำนวนตัวอย่างข้อมูลการฝึกอบรม
Random Over-Sampling - เทคนิคนี้มีจุดมุ่งหมายเพื่อสร้างความสมดุลในการกระจายคลาสโดยการเพิ่มจำนวนอินสแตนซ์ในคลาสของชนกลุ่มน้อยโดยการจำลองแบบ
Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%ในกรณีที่เราจำลองการสังเกตการณ์ที่ฉ้อโกง 50 ครั้ง 30 ครั้งการสังเกตการณ์ที่ฉ้อโกงหลังจากจำลองแบบการสังเกตการณ์ของชนกลุ่มน้อยจะเท่ากับ 1,500 จากนั้นการสังเกตการณ์ทั้งหมดในข้อมูลใหม่หลังจากการสุ่มตัวอย่างเกินจะเท่ากับ 4950 + 1500 = 6450 ดังนั้นอัตราเหตุการณ์สำหรับชุดข้อมูลใหม่ จะเป็น 1500/6450 = 23%
ข้อได้เปรียบหลักของวิธีนี้คือจะไม่มีการสูญเสียข้อมูลที่เป็นประโยชน์ แต่ในทางกลับกันก็มีโอกาสที่จะสวมใส่มากเกินไปเนื่องจากเป็นการจำลองเหตุการณ์ของชนกลุ่มน้อย
เทคนิคทั้งมวล
วิธีการนี้โดยทั่วไปใช้เพื่อแก้ไขอัลกอริทึมการจำแนกที่มีอยู่เพื่อให้เหมาะสมกับชุดข้อมูลที่ไม่สมดุล ในแนวทางนี้เราสร้างตัวจำแนกสองขั้นตอนจากข้อมูลเดิมจากนั้นจึงรวบรวมการคาดการณ์ ลักษณนามฟอเรสต์แบบสุ่มเป็นตัวอย่างของลักษณนามตามทั้งมวล