การแปลงระบบตัวเลข

ดังที่คุณทราบระบบเลขฐานสิบฐานสองฐานแปดและเลขฐานสิบหกเป็นระบบตัวเลขค่าตำแหน่ง ในการแปลงเลขฐานสองฐานแปดและเลขฐานสิบหกเป็นเลขฐานสิบเราเพียงแค่ต้องเพิ่มผลคูณของแต่ละหลักด้วยค่าตำแหน่ง ที่นี่เราจะเรียนรู้การแปลงอื่น ๆ ในระบบตัวเลขเหล่านี้

ทศนิยมเป็นไบนารี

ตัวเลขฐานสิบสามารถแปลงเป็นเลขฐานสองได้โดยการหารจำนวนซ้ำ ๆ ด้วย 2 ในขณะที่บันทึกส่วนที่เหลือ ลองมาเป็นตัวอย่างเพื่อดูว่าสิ่งนี้เกิดขึ้นได้อย่างไร

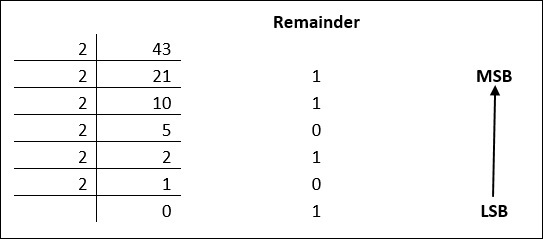
ส่วนที่เหลือจะต้องอ่านจากล่างขึ้นบนเพื่อให้ได้ค่าเทียบเท่าไบนารี

43 ₁₀ = 101011 ₂

ทศนิยมเป็นฐานแปด

ตัวเลขฐานสิบสามารถแปลงเป็นเลขฐานแปดได้โดยการหารจำนวนซ้ำด้วย 8 ในขณะที่บันทึกส่วนที่เหลือ ลองมาเป็นตัวอย่างเพื่อดูว่าสิ่งนี้เกิดขึ้นได้อย่างไร

การอ่านส่วนที่เหลือจากล่างขึ้นบน

473 ₁₀ = 731 ₈

ทศนิยมเป็นเลขฐานสิบหก

ตัวเลขฐานสิบสามารถแปลงเป็นเลขฐานแปดได้โดยการหารตัวเลขซ้ำ 16 ในขณะบันทึกส่วนที่เหลือ ลองมาเป็นตัวอย่างเพื่อดูว่าเกิดขึ้นได้อย่างไร

การอ่านส่วนที่เหลือจากล่างขึ้นบนเราได้

423 ₁₀ = 1A7 ₁₆

ไบนารีเป็นฐานแปดและในทางกลับกัน

ในการแปลงเลขฐานสองเป็นเลขฐานแปดให้ทำตามขั้นตอนเหล่านี้ -

• เริ่มจากบิตที่มีนัยสำคัญน้อยที่สุดให้สร้างกลุ่มสามบิต

• หากมีบิตน้อยกว่าหนึ่งหรือสองบิตในการสร้างกลุ่มสามารถเพิ่ม 0s หลังบิตที่มีนัยสำคัญที่สุดได้

• แปลงแต่ละกลุ่มให้เป็นเลขฐานแปดที่เท่ากัน

ลองมาเป็นตัวอย่างเพื่อทำความเข้าใจนี้

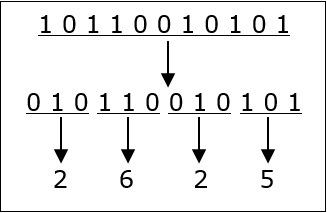
1011001010 ₁₂ = 2625 ₈

ในการแปลงเลขฐานแปดเป็นเลขฐานสองเลขฐานแปดแต่ละตัวจะถูกแปลงเป็นเลขฐานสอง 3 บิตตามตารางนี้

เลขฐานแปด	0	1	2	3	4	5	6	7
เทียบเท่าไบนารี	000	001	010	011	100	101	110	111

54673 ₈ = 101100110111011 ₂

ไบนารีเป็นเลขฐานสิบหก

ในการแปลงเลขฐานสองเป็นเลขฐานสิบหกให้ทำตามขั้นตอนเหล่านี้ -

• เริ่มจากบิตที่มีนัยสำคัญน้อยที่สุดให้สร้างกลุ่มสี่บิต

• หากมีบิตน้อยกว่าหนึ่งหรือสองบิตในการสร้างกลุ่มสามารถเพิ่ม 0s หลังบิตที่มีนัยสำคัญที่สุดได้

• แปลงแต่ละกลุ่มให้เป็นเลขฐานแปดที่เท่ากัน

ลองมาเป็นตัวอย่างเพื่อทำความเข้าใจนี้

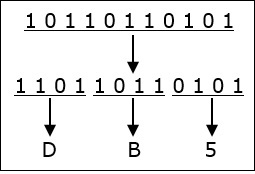
10110110101 ₂ = DB5 ₁₆

ในการแปลงเลขฐานแปดเป็นเลขฐานสองเลขฐานแปดแต่ละตัวจะถูกแปลงเป็นเลขฐานสอง 3 บิต