วิศวกรรมไมโครเวฟ - เสื้อยืด E-Plane
ทางแยก E-Plane Tee เกิดขึ้นจากการติดท่อนำคลื่นธรรมดาเข้ากับมิติที่กว้างขึ้นของท่อนำคลื่นสี่เหลี่ยมซึ่งมีสองพอร์ตอยู่แล้ว แขนของท่อนำคลื่นสี่เหลี่ยมสร้างสองพอร์ตที่เรียกว่าcollinear ports กล่าวคือ Port1 และ Port2 ในขณะที่พอร์ตใหม่ Port3 เรียกว่า Side arm หรือ E-arm. เสื้อยืด E-plane ของเขาเรียกอีกอย่างว่าSeries Tee.
เนื่องจากแกนของแขนด้านข้างขนานกับสนามไฟฟ้าทางแยกนี้จึงเรียกว่า E-Plane Tee junction นี้เรียกอีกอย่างว่าVoltage หรือ Series junction. พอร์ต 1 และ 2 อยู่ห่างจากเฟส 180 °ซึ่งกันและกัน รายละเอียดหน้าตัดของ E-plane tee สามารถเข้าใจได้จากรูปต่อไปนี้
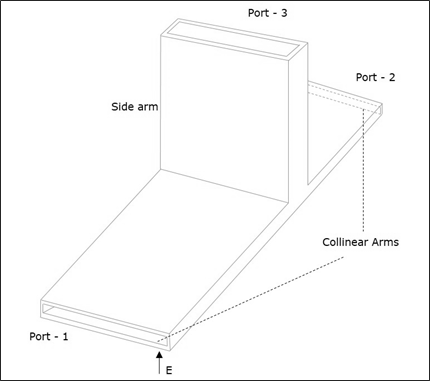
รูปต่อไปนี้แสดงการเชื่อมต่อที่ทำโดย sidearm กับท่อนำคลื่นสองทิศทางเพื่อสร้างพอร์ตขนาน
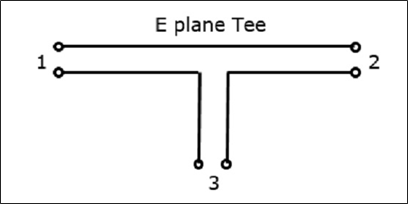
คุณสมบัติของเสื้อยืด E-Plane
คุณสมบัติของ E-Plane Tee สามารถกำหนดได้โดย $ [S] _ {3x3} $ matrix
เป็นเมทริกซ์ 3 × 3 เนื่องจากมี 3 อินพุตที่เป็นไปได้และ 3 เอาต์พุตที่เป็นไปได้
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {21} & S_ {22} & S_ {23} \\ S_ {31} & S_ {32 } & S_ {33} \ end {bmatrix} $ ........ Equation 1
ค่าสัมประสิทธิ์การกระจาย $ S_ {13} $ และ $ S_ {23} $ อยู่นอกเฟส 180 °ด้วยอินพุตที่พอร์ต 3
$ S_ {23} = -S_ {13} $........ Equation 2
พอร์ตจับคู่กับทางแยกได้อย่างสมบูรณ์แบบ
$ S_ {33} = 0 $........ Equation 3
จากคุณสมบัติสมมาตร
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21} \: \: S_ {23} = S_ {32} \: \: S_ {13} = S_ {31} $........ Equation 4
เมื่อพิจารณาสมการ 3 และ 4 เมทริกซ์ $ [S] $ สามารถเขียนเป็น
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & -S_ {13} \\ S_ {13} & -S_ {13} & 0 \ end {bmatrix} $........ Equation 5
เราสามารถพูดได้ว่าเรามีสิ่งที่ไม่รู้จักสี่ตัวเมื่อพิจารณาจากคุณสมบัติสมมาตร
จากคุณสมบัติ Unitary
$$ [S] [S] \ ast = [I] $$
$$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & -S_ {13} \\ S_ {13} & -S_ {13} & 0 \ end {bmatrix} \: \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & -S_ {13} ^ {*} \\ S_ {13} ^ {*} & -S_ {13} ^ {*} & 0 \ end {bmatrix} = \ begin { bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
การคูณที่เราได้รับ
(สังเกต R เป็นแถวและ C เป็นคอลัมน์)
$ R_1C_1: S_ {11} S_ {11} ^ {*} + S_ {12} S_ {12} ^ {*} + S_ {13} S_ {13} ^ {*} = 1 $
$ \ left | S_ {11} \ right | ^ 2 + \ left | S_ {11} \ right | ^ 2 + \ left | S_ {11} \ right | ^ 2 = 1 $........ Equation 6
$ R_2C_2: \ left | S_ {12} \ right | ^ 2 + \ left | S_ {22} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $......... Equation 7
$ R_3C_3: \ left | S_ {13} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $......... Equation 8
$ R_3C_1: S_ {13} S_ {11} ^ {*} - S_ {13} S_ {12} ^ {*} = 1 $ ......... Equation 9
เราได้สมการที่ 6 และ 7
$ S_ {11} = S_ {22} $ ......... Equation 10
จากสมการ 8
เหลือ $ 2 | S_ {13} \ right | ^ 2 \ quad หรือ \ quad S_ {13} = \ frac {1} {\ sqrt {2}} $......... Equation 11
จากสมการ 9
$ S_ {13} \ left (S_ {11} ^ {*} - S_ {12} ^ {*} \ right) $
หรือ $ S_ {11} = S_ {12} = S_ {22} $ ......... Equation 12
โดยใช้สมการ 10, 11 และ 12 ในสมการ 6
เราได้รับ,
$ \ left | S_ {11} \ right | ^ 2 + \ left | S_ {11} \ right | ^ 2 + \ frac {1} {2} = 1 $
เหลือ $ 2 | S_ {11} \ right | ^ 2 = \ frac {1} {2} $
หรือ $ S_ {11} = \ frac {1} {2} $ ......... Equation 13
การแทนค่าจากสมการข้างต้นใน $ [S] $ matrix
เราได้รับ,
$$ \ left [S \ right] = \ begin {bmatrix} \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac { 1} {2} & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & - \ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix} $$
เรารู้ว่า $ [b] $ = $ [S] [a] $
$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ begin {bmatrix} \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {2} & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2 }} & - \ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix} $$
นี่คือเมทริกซ์การกระจายของ E-Plane Tee ซึ่งอธิบายคุณสมบัติการกระเจิงของมัน