วิศวกรรมไมโครเวฟ - สายส่ง
ก transmission lineเป็นตัวเชื่อมต่อที่ส่งพลังงานจากจุดหนึ่งไปยังอีกจุดหนึ่ง การศึกษาทฤษฎีสายส่งมีประโยชน์ในการใช้พลังงานและอุปกรณ์อย่างมีประสิทธิภาพ
โดยทั่วไปมีสายส่งสี่ประเภท -
- สายส่งแบบขนานสองสาย
- เส้นโคแอกเชียล
- สายส่งพื้นผิวชนิดสตริป
- Waveguides
ในขณะที่ส่งหรือขณะรับการถ่ายโอนพลังงานจะต้องทำได้อย่างมีประสิทธิภาพโดยไม่ต้องสูญเสียพลังงาน เพื่อให้บรรลุเป้าหมายนี้มีพารามิเตอร์ที่สำคัญบางประการที่ต้องพิจารณา
พารามิเตอร์หลักของสายส่ง
พารามิเตอร์ที่สำคัญของสายส่งคือความต้านทานความเหนี่ยวนำความจุและการนำไฟฟ้า
ความต้านทานและการเหนี่ยวนำรวมกันเรียกว่าสายส่ง impedance.
ความจุและการนำไฟฟ้ารวมกันเรียกว่า admittance.
ความต้านทาน
ความต้านทานที่นำเสนอโดยวัสดุที่ใช้ทำสายส่งจะมีจำนวนมากโดยเฉพาะอย่างยิ่งสำหรับสายที่สั้นกว่า เมื่อกระแสของสายเพิ่มขึ้นการสูญเสียโอห์มมิค $ \ left (I ^ {2} R \: loss \ right) $ ก็เพิ่มขึ้นเช่นกัน
ความต้านทาน $R$ ของตัวนำความยาว "$l$" และหน้าตัด "$a$" แสดงเป็น
$$ R = \ rho \ frac {l} {a} $$
ที่ไหน
Ѓ $ \ rho $ = ความต้านทานของวัสดุตัวนำซึ่งคงที่
อุณหภูมิและความถี่ของกระแสไฟฟ้าเป็นปัจจัยหลักที่มีผลต่อความต้านทานของเส้น ความต้านทานของตัวนำจะแปรผันตามการเปลี่ยนแปลงของอุณหภูมิ ในขณะที่ถ้าความถี่ของกระแสไฟฟ้าเพิ่มขึ้นความหนาแน่นของกระแสไฟฟ้าที่มีต่อพื้นผิวของตัวนำก็จะเพิ่มขึ้นด้วย มิฉะนั้นความหนาแน่นของกระแสไฟฟ้าต่อศูนย์กลางของตัวนำจะเพิ่มขึ้น
ซึ่งหมายความว่ายิ่งกระแสไหลไปที่พื้นผิวของตัวนำกระแสไฟฟ้าก็จะไหลเข้าหาศูนย์กลางน้อยลงซึ่งเรียกว่า Skin Effect.
ตัวเหนี่ยวนำ
ในสายส่งไฟฟ้ากระแสสลับกระแสจะไหลในรูปแบบไซน์ กระแสไฟฟ้านี้ทำให้เกิดสนามแม่เหล็กตั้งฉากกับสนามไฟฟ้าซึ่งแตกต่างกันไปตามรูปไซน์ สิ่งนี้เป็นที่รู้จักกันดีในนามกฎของฟาราเดย์ ฟิลด์จะแสดงในรูปต่อไปนี้

สนามแม่เหล็กที่แตกต่างกันนี้จะเหนี่ยวนำ EMF บางส่วนเข้าสู่ตัวนำ ตอนนี้แรงดันไฟฟ้าที่เหนี่ยวนำหรือ EMF จะไหลไปในทิศทางตรงกันข้ามกับกระแสที่ไหลในตอนแรก EMF ที่ไหลไปในทิศทางตรงกันข้ามจะแสดงโดยพารามิเตอร์ที่เรียกว่าInductanceซึ่งเป็นคุณสมบัติในการต่อต้านการเปลี่ยนแปลงในปัจจุบัน
แสดงโดย "L". หน่วยวัดคือ"Henry(H)".
ความประพฤติ
จะมีกระแสรั่วไหลระหว่างสายส่งและสายดินและระหว่างตัวนำเฟสด้วย โดยทั่วไปกระแสไฟฟ้ารั่วจำนวนเล็กน้อยนี้จะไหลผ่านพื้นผิวของฉนวน ผกผันของกระแสไฟฟ้ารั่วนี้เรียกว่าConductance. แสดงโดย "G".
การไหลของกระแสไฟฟ้ามีความสัมพันธ์กับการเหนี่ยวนำและความแตกต่างของแรงดันไฟฟ้าระหว่างจุดทั้งสองนั้นสัมพันธ์กับความจุ ตัวเหนี่ยวนำเกี่ยวข้องกับสนามแม่เหล็กในขณะที่ความจุสัมพันธ์กับสนามไฟฟ้า
ความจุ
ความต่างศักย์ระหว่าง Phase conductorsก่อให้เกิดสนามไฟฟ้าระหว่างตัวนำ ตัวนำทั้งสองก็เหมือนกับเพลตขนานและอากาศที่อยู่ระหว่างนั้นจะกลายเป็นอิเล็กทริก รูปแบบนี้ก่อให้เกิดผลของความจุระหว่างตัวนำ
ความต้านทานลักษณะ
หากพิจารณาสายส่งแบบไม่สูญเสียแบบสม่ำเสมอสำหรับคลื่นที่เคลื่อนที่ไปในทิศทางเดียวอัตราส่วนของแอมพลิจูดของแรงดันและกระแสตามแนวนั้นซึ่งไม่มีการสะท้อนกลับจะเรียกว่าเป็น Characteristic impedance.
แสดงด้วย $ Z_0 $
$$ Z_0 = \ sqrt {\ frac {แรงดันไฟฟ้า \: \: wave \: \: value} {current \: \: wave \: \: value}} $$
$$ Z_0 = \ sqrt {\ frac {R + jwL} {G + jwC}} $$
สำหรับเส้นที่ไม่มีการสูญเสีย $ R_0 = \ sqrt {\ frac {L} {C}} $
โดยที่ $ L $ & $ C $ คือการเหนี่ยวนำและความจุต่อหน่วยความยาว
การจับคู่ความต้านทาน
เพื่อให้เกิดการถ่ายโอนพลังงานสูงสุดไปยังโหลดต้องทำการจับคู่อิมพีแดนซ์ เพื่อให้บรรลุการจับคู่อิมพีแดนซ์นี้จะต้องปฏิบัติตามเงื่อนไขต่อไปนี้
ความต้านทานของโหลดควรเท่ากับของแหล่งที่มา
$$ R_L = R_S $$
รีแอคแตนซ์ของโหลดควรเท่ากับของแหล่งกำเนิด แต่ตรงข้ามกันในเครื่องหมาย
$$ X_L = -X_S $$
ซึ่งหมายความว่าถ้าแหล่งที่มาเป็นอุปนัยโหลดควรเป็นแบบ capacitive และในทางกลับกัน
การสะท้อนร่วมที่มีประสิทธิภาพ
พารามิเตอร์ที่แสดงปริมาณพลังงานที่สะท้อนกลับเนื่องจากความต้านทานไม่ตรงกันในสายส่งเรียกว่า Reflection coefficient. ระบุโดย $ \ rho $(rho).
สามารถกำหนดเป็น "อัตราส่วนของแรงดันไฟฟ้าสะท้อนต่อแรงดันตกกระทบที่ขั้วโหลด"
$$ \ rho = \ frac {สะท้อน \: แรงดันไฟฟ้า} {เหตุการณ์ \: แรงดันไฟฟ้า} = \ frac {V_r} {V_i} \: ที่ \: load \: ขั้ว $$
หากอิมพีแดนซ์ระหว่างอุปกรณ์และสายส่งไม่ตรงกันพลังงานจะสะท้อนออกมา ยิ่งพลังงานได้รับการสะท้อนมากเท่าใดค่าสัมประสิทธิ์การสะท้อนของ $ \ rho $ ก็จะยิ่งมากขึ้น
อัตราส่วนคลื่นแรงดันไฟฟ้า (VSWR)
คลื่นนิ่งจะเกิดขึ้นเมื่อคลื่นตกกระทบสะท้อนออกไป คลื่นนิ่งที่ก่อตัวขึ้นมีแรงดันไฟฟ้าบางส่วน ขนาดของคลื่นนิ่งสามารถวัดได้ในรูปของอัตราส่วนคลื่นนิ่ง
อัตราส่วนของแรงดันไฟฟ้าสูงสุดต่อแรงดันไฟฟ้าต่ำสุดในคลื่นนิ่งสามารถกำหนดเป็น Voltage Standing Wave Ratio (VSWR) แสดงโดย "$ S $"
$$ S = \ frac {\ left | V_ {max} \ right |} {\ left | V_ {min} \ right |} \ quad 1 \: \ leq S \ leq \ infty $$
VSWR อธิบายรูปแบบคลื่นนิ่งของแรงดันไฟฟ้าที่มีอยู่ในสายส่งเนื่องจากการเพิ่มเฟสและการลบของเหตุการณ์และคลื่นสะท้อน
ดังนั้นจึงสามารถเขียนเป็นไฟล์
$$ S = \ frac {1 + \ rho} {1 - \ rho} $$
ยิ่งค่าอิมพีแดนซ์ไม่ตรงกันมากเท่าใดแอมพลิจูดของคลื่นนิ่งก็จะยิ่งสูงขึ้นเท่านั้น ดังนั้นหากอิมพีแดนซ์ถูกจับคู่อย่างสมบูรณ์
$$ V_ {max}: V_ {min} = 1: 1 $$
ดังนั้นค่าของ VSWR จึงเป็นเอกภาพซึ่งหมายความว่าการส่งผ่านนั้นสมบูรณ์แบบ
ประสิทธิภาพของสายส่ง
ประสิทธิภาพของสายส่งถูกกำหนดให้เป็นอัตราส่วนของกำลังขับต่อกำลังไฟฟ้าเข้า
$ \% \: efficiency \: of \: transmission \: line \: \ eta = \ frac {Power \: ส่ง \: at \: reception} {Power \: sent \: from \: the \: transmission \: end} \ คูณ 100 $
การควบคุมแรงดันไฟฟ้า
การควบคุมแรงดันไฟฟ้าหมายถึงการเปลี่ยนแปลงขนาดของแรงดันไฟฟ้าระหว่างปลายส่งและรับของสายส่ง
$ \% \: แรงดัน \: ระเบียบ = \ frac {ส่ง \: end \: แรงดันไฟฟ้า - \: รับ \: end \: แรงดันไฟฟ้า} {ส่ง \: end \: voltage} \ คูณ 100 $
การสูญเสียเนื่องจากความต้านทานไม่ตรงกัน
สายส่งหากไม่สิ้นสุดด้วยโหลดที่ตรงกันจะเกิดการสูญเสีย การสูญเสียเหล่านี้มีหลายประเภทเช่นการสูญเสียการลดทอนการสูญเสียการสะท้อนการสูญเสียการส่งการสูญเสียการส่งคืนการสูญเสียการแทรก ฯลฯ
การสูญเสียการลดทอน
การสูญเสียที่เกิดขึ้นเนื่องจากการดูดซับสัญญาณในสายส่งเรียกว่าการสูญเสียการลดทอนซึ่งแสดงเป็น
$$ การลดทอน \: loss (dB) = 10 \: log_ {10} \ left [\ frac {E_i - E_r} {E_t} \ right] $$
ที่ไหน
$ E_i $ = พลังงานอินพุต
$ E_r $ = พลังงานที่สะท้อนจากโหลดไปยังอินพุต
$ E_t $ = พลังงานที่ส่งไปยังโหลด
การสูญเสียการสะท้อน
การสูญเสียที่เกิดขึ้นเนื่องจากการสะท้อนของสัญญาณเนื่องจากความต้านทานไม่ตรงกันของสายส่งเรียกว่าการสูญเสียการสะท้อนซึ่งแสดงเป็น
$$ Reflection \: loss (dB) = 10 \: log_ {10} \ left [\ frac {E_i} {E_i - E_r} \ right] $$
ที่ไหน
$ E_i $ = พลังงานอินพุต
$ E_r $ = พลังงานสะท้อนจากโหลด
การสูญเสียการส่ง
การสูญเสียที่เกิดขึ้นขณะส่งผ่านสายส่งเรียกว่า Transmission loss ซึ่งแสดงเป็น
$$ Transmission \: loss (dB) = 10 \: log_ {10} \: \ frac {E_i} {E_t} $$
ที่ไหน
$ E_i $ = พลังงานอินพุต
$ E_t $ = พลังงานที่ส่งผ่าน
การสูญเสียกลับ
การวัดกำลังที่สะท้อนจากสายส่งเรียกว่าการสูญเสียผลตอบแทนซึ่งแสดงเป็น
$$ Return \: loss (dB) = 10 \: log_ {10} \: \ frac {E_i} {E_r} $$
ที่ไหน
$ E_i $ = พลังงานอินพุต
$ E_r $ = พลังงานที่สะท้อนกลับ
การสูญเสียการแทรก
การสูญเสียที่เกิดขึ้นเนื่องจากการถ่ายเทพลังงานโดยใช้สายส่งเมื่อเทียบกับการถ่ายเทพลังงานโดยไม่มีสายส่งเรียกว่าการสูญเสียการแทรกซึ่งแสดงเป็น
$$ Insertion \: loss (dB) = 10 \: log_ {10} \: \ frac {E_1} {E_2} $$
ที่ไหน
$ E_1 $ = พลังงานที่โหลดได้รับเมื่อเชื่อมต่อโดยตรงกับแหล่งที่มาโดยไม่มีสายส่ง
$ E_2 $ = พลังงานที่โหลดได้รับเมื่อสายส่งเชื่อมต่อระหว่างโหลดและแหล่งที่มา
Stub Matching
หากอิมพีแดนซ์ของโหลดไม่ตรงกับอิมพีแดนซ์ต้นทางบางครั้งก็ใช้วิธีที่เรียกว่า "Stub Matching" เพื่อให้ได้การจับคู่
กระบวนการเชื่อมต่อส่วนของสายเปิดหรือลัดวงจรที่เรียกว่า stubs ในการปัดด้วยเส้นหลักในบางจุดหรือบางจุดสามารถเรียกได้ว่าเป็น Stub Matching.
ที่ความถี่ไมโครเวฟที่สูงขึ้นโดยทั่วไปจะใช้เทคนิคการจับคู่ต้นขั้วสองแบบ
การจับคู่ Stub เดียว
ในการจับคู่แบบ Single Stub จะมีการวางต้นขั้วที่มีความยาวคงที่ที่ระยะห่างจากโหลด ใช้สำหรับความถี่คงที่เท่านั้นเนื่องจากสำหรับการเปลี่ยนแปลงความถี่ใด ๆ จะต้องมีการเปลี่ยนตำแหน่งของต้นขั้วซึ่งไม่ได้ทำ วิธีนี้ไม่เหมาะสำหรับสายโคแอกเชียล
การจับคู่ Stub คู่
ในการจับคู่สตั๊ดคู่ความยาวตัวแปรสองเส้นจะถูกกำหนดไว้ที่บางตำแหน่ง เมื่อโหลดเปลี่ยนไปจะมีการปรับเฉพาะความยาวของส่วนต่อเพื่อให้ได้การจับคู่ สิ่งนี้ใช้กันอย่างแพร่หลายในห้องปฏิบัติการเป็นอุปกรณ์จับคู่ความถี่เดียว
ตัวเลขต่อไปนี้แสดงให้เห็นว่าการจับคู่ของต้นขั้วมีลักษณะอย่างไร
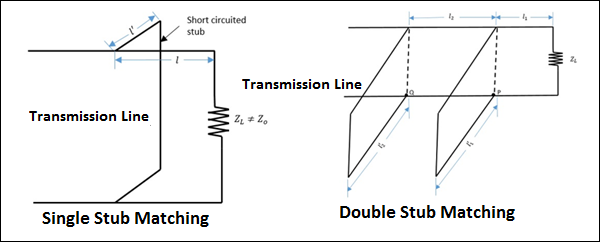
การจับคู่ต้นขั้วเดี่ยวและการจับคู่ต้นขั้วคู่ดังที่แสดงในรูปด้านบนจะกระทำในสายส่งเพื่อให้เกิดการจับคู่อิมพีแดนซ์