การพล็อตจำนวนตรรกยะบนเส้นจำนวน
จำนวนตรรกยะคือเศษส่วนและมีการพล็อตบนเส้นจำนวนดังนี้
Basic rules of representing rational no. on number line
ถ้าเลขที่เป็นเหตุเป็นผล (เศษส่วน) เหมาะสมแล้วมันจะอยู่ระหว่าง 0 ถึง 1
หากเลขที่เป็นเหตุเป็นผล (เศษส่วน) ไม่เหมาะสมอันดับแรกเราจะแปลงเป็นเศษส่วนผสมจากนั้นจึงหาเลขที่มีเหตุผล อยู่ระหว่างจำนวนเต็มและจำนวนเต็มถัดไป
เราใช้ขั้นตอนต่อไปนี้เพื่อแสดงจำนวนหรือเศษส่วนที่มีเหตุผลตัวอย่างเช่น$ \ frac {5} {7} $ในบรรทัดตัวเลข
Step 1 - เราวาดเส้นจำนวน
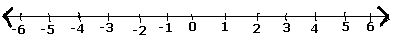
Step 2- เนื่องจากตัวเลข$ \ frac {5} {7} $เป็นจำนวนบวกจึงอยู่ทางด้านขวาของศูนย์
Step 3- หลังจากเครื่องหมายศูนย์เราจะมี$ \ frac {1} {7}, \: \ frac {2} {7}, \: \ frac {3} {7}, \: \ frac {4} {7 }, \: \ frac {5} {7}, \: \ frac {6} {7}, $และ ( $ \ frac {7} {7} $ = 1)
Step 4- จำนวนเหตุผล$ \ frac {5} {7} $ในบรรทัดตัวเลขจะแสดงดังนี้

พล็อต$ \ frac {1} {4} $และ$ 1 \ frac {2} {4} $ในบรรทัดตัวเลขด้านล่าง
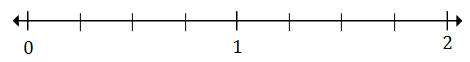
วิธีการแก้
Step 1:
$ \ frac {1} {4} $ (A) อยู่ระหว่าง 0 ถึง 1; $ 1 \ frac {2} {4} $ (B) อยู่ระหว่าง 1 ถึง 2
Step 2:
การหารแต่ละครั้งจะแบ่งออกเป็นสี่ส่วนเนื่องจากด้านล่างของเศษส่วนคือ 4
$ \ frac {1} {4} $คือเครื่องหมายแรกหลัง 0 ดังนั้นจุด A จึงแทน$ \ frac {1} {4} $
$ 1 \ frac {2} {4} $คือเครื่องหมายที่สองหลังจาก 1 ดังนั้นจุด B จึงแทน$ 1 \ frac {2} {4} $
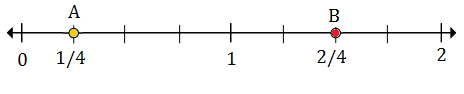
พล็อต$ \ frac {5} {8} $และ$ 2 \ frac {3} {8} $ในบรรทัดตัวเลขด้านล่าง
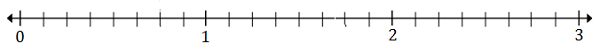
วิธีการแก้
Step 1:
$ \ frac {5} {8} $ 8 (A) อยู่ระหว่าง 0 ถึง 1; $ 2 \ frac {3} {8} $ (B) อยู่ระหว่าง 2 ถึง 3
Step 2:
การหารแต่ละส่วนแบ่งออกเป็นแปดส่วนโดยด้านล่างของเศษส่วนคือ 8
$ \ frac {5} {8} $คือเครื่องหมายที่ห้าหลัง 0 ดังนั้นจุด A จึงแทน$ \ frac {5} {8} $
$ 2 \ frac {3} {8} $คือเครื่องหมายที่สามหลังจาก 2 ดังนั้นจุด B จึงแทน$ 2 \ frac {3} {8} $
