เครื่องใช้ไฟฟ้า - เครื่องสับ
เครื่องสับใช้ความเร็วสูงในการเชื่อมต่อและตัดการเชื่อมต่อจากโหลดต้นทาง แรงดันไฟฟ้ากระแสตรงคงที่จะใช้กับโหลดต้นทางเป็นระยะ ๆ โดยการเปิด / ปิดสวิตช์เปิด / ปิดอย่างต่อเนื่อง ช่วงเวลาที่สวิตช์เปิด / ปิดค้างอยู่เรียกว่าเวลาสถานะเปิดและปิดของสับตามลำดับ
เครื่องบดสับส่วนใหญ่จะใช้กับรถยนต์ไฟฟ้าการแปลงพลังงานลมและแสงอาทิตย์และตัวควบคุมมอเตอร์กระแสตรง
สัญลักษณ์ของ Chopper
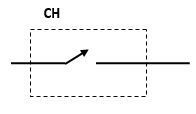
การจำแนกประเภทของ Choppers
ขึ้นอยู่กับเอาท์พุทแรงดันไฟฟ้าตัวสับถูกจัดประเภทเป็น -
- Step Up Chopper (ตัวแปลงเพิ่ม)
- Step Down Chopper (ตัวแปลงบั๊ก)
- Step Up / Down Chopper (ตัวแปลง Buck-boost)
Step Up Chopper
เอาต์พุตแรงดันไฟฟ้าเฉลี่ย (V o ) ในตัวสับแบบ step up มีค่ามากกว่าแรงดันไฟฟ้าอินพุต (V s ) รูปด้านล่างแสดงการกำหนดค่าของตัวสับแบบ step up
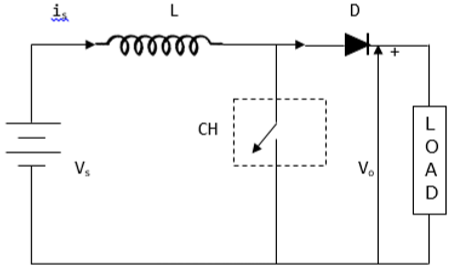
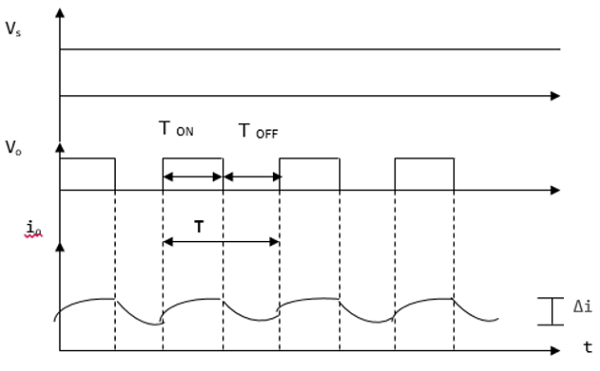
รูปคลื่นกระแสและแรงดัน
V 0 (เอาท์พุทแรงดันไฟฟ้าเฉลี่ย) เป็นบวกเมื่อสับเปิดและลบเมื่อสับปิดอยู่ดังแสดงในรูปคลื่นด้านล่าง
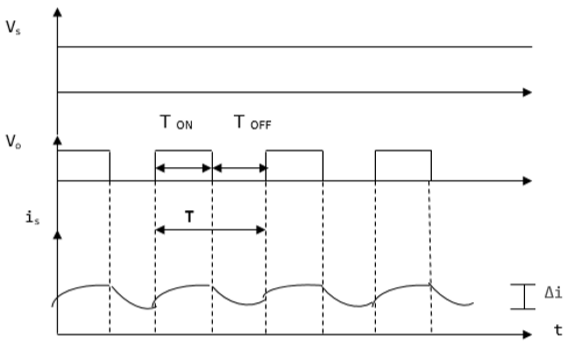
ที่ไหน
T ON - ช่วงเวลาที่สับเปิดอยู่
T OFF - ช่วงเวลาเมื่อปิดเครื่องสับ
V L - โหลดแรงดันไฟฟ้า
V s - แรงดันไฟฟ้าที่มา
T - ช่วงเวลาการสับ = T ON + T OFF
V oให้โดย -
$$ V_ {0} = \ frac {1} {T} \ int_ {0} ^ {T_ {ON}} V_ {S} dt $$เมื่อสับ (CH) เปิดอยู่โหลดจะลัดวงจรดังนั้นแรงดันไฟฟ้าขาออกสำหรับช่วงเวลาดังกล่าว TONเป็นศูนย์ นอกจากนี้ตัวเหนี่ยวนำจะถูกชาร์จในช่วงเวลานี้ สิ่งนี้ให้ V S = V L
$ L \ frac {di} {dt} = V_ {S}, $ $ \ frac {\ Delta i} {T_ {ON}} = \ frac {V_ {S}} {L} $
ดังนั้น$ \ Delta i = \ frac {V_ {S}} {L} T_ {ON} $
Δi = คือจุดสูงสุดของตัวเหนี่ยวนำจนถึงจุดสูงสุดในปัจจุบัน เมื่อสับ (CH) ปิดอยู่การคายประจุจะเกิดขึ้นผ่านตัวเหนี่ยวนำ L ดังนั้นผลรวมของ V sและ V Lจะได้รับดังนี้ -
$ V_ {0} = V_ {S} + V_ {L}, \ quad V_ {L} = V_ {0} -V_ {S} $
แต่$ L \ frac {di} {dt} = V_ {0} -V_ {S} $
ดังนั้น$ L \ frac {\ Delta i} {T_ {OFF}} = V_ {0} -V_ {S} $
สิ่งนี้ทำให้$ \ Delta i = \ frac {V_ {0} -V_ {S}} {L} T_ {OFF} $
การเท่ากับΔiจากสถานะเปิดเป็นΔiจากสถานะปิดจะให้ -
$ \ frac {V_ {S}} {L} T_ {ON} = \ frac {V_ {0} -V_ {S}} {L} T_ {OFF} $, $ V_ {S} \ left (T_ {ON } + T_ {OFF} \ right) = V_ {0} T_ {OFF} $
$ V_ {0} = \ frac {TV_ {S}} {T_ {OFF}} = \ frac {V_ {S}} {\ frac {\ left (T + T_ {ON} \ right)} {T}} $
สิ่งนี้ให้แรงดันไฟฟ้าเฉลี่ยเป็น
$$ V_ {0} = \ frac {V_ {S}} {1-D} $$สมการข้างต้นแสดงให้เห็นว่า V oสามารถแปรผันได้ตั้งแต่ V Sถึงอินฟินิตี้ มันพิสูจน์ได้ว่าแรงดันไฟฟ้าขาออกจะมากกว่าแรงดันไฟฟ้าขาเข้าเสมอดังนั้นจึงเพิ่มหรือเพิ่มระดับแรงดันไฟฟ้า
ขั้นตอนลง Chopper
สิ่งนี้เรียกอีกอย่างว่าตัวแปลงบั๊ก ในสับนี้แรงดันเอาท์พุทเฉลี่ย V Oน้อยกว่าแรงดันไฟฟ้าอินพุต V S เมื่อเครื่องบดสับเปิดอยู่ V O = V Sและเมื่อเครื่องสับปิดอยู่ V O = 0
เมื่อเครื่องบดสับเปิดอยู่ -
$ V_ {S} = \ left (V_ {L} + V_ {0} \ right), \ quad V_ {L} = V_ {S} -V_ {0}, \ quad L \ frac {di} {dt} = V_ {S} -V_ {0}, \ quad L \ frac {\ Delta i} {T_ {ON}} = V_ {s} + V_ {0} $
ดังนั้นโหลดกระแสสูงสุดถึงจุดสูงสุดจะได้รับจาก
$ \ Delta i = \ frac {V_ {s} -V_ {0}} {L} T_ {ON} $
แผนภูมิวงจรรวม
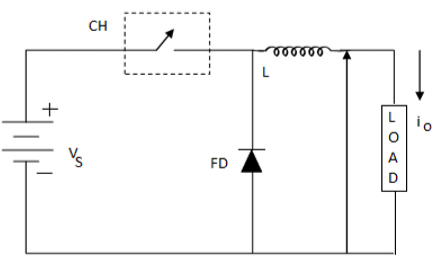
ที่ไหน FD คือไดโอดล้อหมุนฟรี
เมื่อตัวสับปิดอยู่การกลับขั้วและการคายประจุจะเกิดขึ้นที่ตัวเหนี่ยวนำ กระแสจะผ่านไดโอดล้ออิสระและตัวเหนี่ยวนำไปยังโหลด สิ่งนี้ให้
$$ L \ frac {ดิ} {dt} = V_ {0} .................................. ...... \ left (i \ right) $$เขียนใหม่เป็น - $ \ quad L \ frac {\ Delta i} {T_ {OFF}} = V_ {0} $
$$ \ Delta i = V_ {0} \ frac {T_ {OFF}} {L} ............................. ...... \ left (ii \ right) $$สมการสมการ (i) และ (ii) ให้;
$ \ frac {V_ {S} -V_ {0}} {L} T_ {ON} = \ frac {V_ {0}} {L} T_ {OFF} $
$ \ frac {V_ {S} -V_ {0}} {V_ {0}} = \ frac {T_ {OFF}} {T_ {ON}} $
$ \ frac {V_ {S}} {V_ {0}} = \ frac {T_ {ON} -T_ {OFF}} {T_ {ON}} $
สมการข้างต้นให้;
$$ V_ {0} = \ frac {T_ {ON}} {T} V_ {S} = DV_ {S} $$สมการ (i) ให้ -
$ \ Delta i = \ frac {V_ {S} -DV_ {S}} {L} DT $ จาก $ D = \ frac {T_ {ON}} {T} $
$ = \ frac {V_ {S} - \ left (1-D \ right) D} {Lf} $
$ f = \ frac {1} {T} = $ สับถี่
รูปคลื่นกระแสและแรงดัน
รูปคลื่นกระแสและแรงดันแสดงไว้ด้านล่าง -
สำหรับการสับแบบ step down แรงดันไฟฟ้าขาออกจะน้อยกว่าแรงดันไฟฟ้าขาเข้าเสมอ แสดงโดยรูปคลื่นด้านล่าง
Step Up / Step Down Chopper
สิ่งนี้เรียกอีกอย่างว่าตัวแปลง buck-boost ทำให้สามารถเพิ่มหรือลดระดับแรงดันไฟฟ้าเข้าได้ แผนภาพด้านล่างแสดงตัวสับเพิ่มบัค
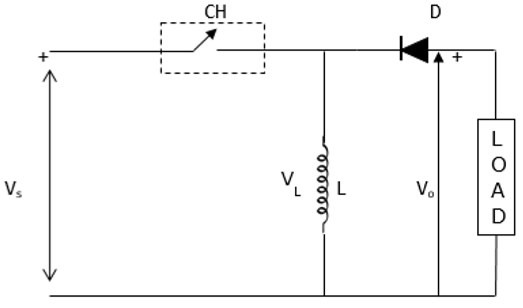
เมื่อสับเปิดอยู่ที่เหนี่ยวนำ L กลายเป็นเรียกเก็บโดยแหล่งที่มาของแรงดันไฟฟ้า V s ดังนั้น V s = V L
$$ L \ frac {di} {dt} = V_ {S} $$ $$ \ Delta i = \ frac {V_ {S}} {L} T_ {ON} = \ frac {V_ {S}} {L } T \ frac {T_ {ON}} {T} = \ frac {DV_ {S}} {Lf} $$เพราะว่า -
$ D = \ frac {T_ {ON}} {T} $ และ$ f = \ frac {1} {T} ....................... ....................... \ left (iii \ right) $
เมื่อปิดเครื่องบดสับขั้วของตัวเหนี่ยวนำจะกลับด้านและทำให้คายประจุผ่านไดโอดและโหลด
ดังนั้น
$$ V_ {0} = - V_ {L} $$ $$ L \ frac {di} {dt} = - V_ {0} $$$ L \ frac {\ Delta i} {T_ {OFF}} = - V_ {0} $ ดังนั้น $ \ Delta i = - \ frac {V_ {0}} {L} T_ {OFF} ..... ........................... \ ซ้าย (iv \ ขวา) $
การประเมินสมการ (iii) และ (iv) ให้ -
$ \ frac {DV_ {S}} {Lf} = - \ frac {V_ {0}} {L} T_ {OFF} $, $ DV_ {S} = - DV_ {S} = - V_ {0} T_ { OFF} f $
$ DV_ {S} = - V_ {0} \ frac {T-T_ {ON}} {T} = - V_ {0} \ left (1- \ frac {T_ {ON}} {T} \ right) $ , $ V_ {0} = - \ frac {DV_ {S}} {1-D} $
เพราะ$ D = \ frac {T_ {ON}} {T} = \ frac {T-T_ {OFF}} {1-D} $
สิ่งนี้ให้
$ V_ {0} = \ frac {DV_ {S}} {1-D} $
D สามารถเปลี่ยนแปลงได้ตั้งแต่ 0 ถึง 1 เมื่อ D = 0; V O = 0
เมื่อ D = 0.5, V O = V S
เมื่อ D = 1, V O = ∞
ดังนั้นในช่วง 0 ≤ D ≤ 0.5 แรงดันขาออกจะแตกต่างกันไปในช่วง 0 ≤ V O <V Sและเราจะลดขั้นตอนลงหรือการทำงานของบั๊ก ในขณะที่ในช่วง 0.5 ≤ D ≤ 1 แรงดันขาออกจะแตกต่างกันไปในช่วง V S ≤ V O ≤∞และเราจะได้รับการเพิ่มขึ้นหรือเพิ่มขึ้น