การมอดูเลตแอมพลิจูด

ในบรรดาเทคนิคการมอดูเลตประเภทหลักคือการมอดูเลตคลื่นต่อเนื่องและการมอดูเลตแบบพัลส์ เทคนิคการมอดูเลตคลื่นต่อเนื่องแบ่งออกเป็นAmplitude Modulation และ Angle Modulation.

คลื่นต่อเนื่องดำเนินไปอย่างต่อเนื่องโดยไม่มีช่วงเวลาใด ๆ และเป็นสัญญาณข้อความเบสแบนด์ซึ่งมีข้อมูล คลื่นนี้จะต้องมีการมอดูเลต

ตามคำจำกัดความมาตรฐาน "ความกว้างของสัญญาณพาหะจะแตกต่างกันไปตามแอมพลิจูดของสัญญาณมอดูเลตในทันที" ซึ่งหมายความว่าแอมพลิจูดของสัญญาณพาหะซึ่งไม่มีข้อมูลแตกต่างกันไปตามความกว้างของสัญญาณในแต่ละช่วงเวลาซึ่งมีข้อมูล สิ่งนี้สามารถอธิบายได้ดีจากตัวเลขต่อไปนี้

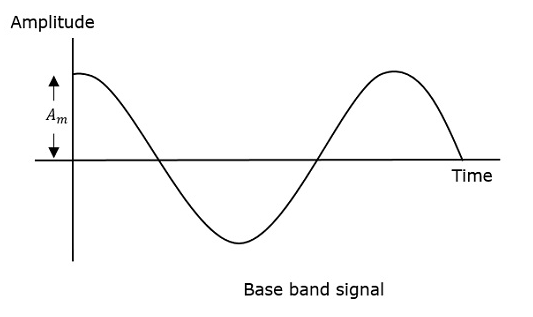
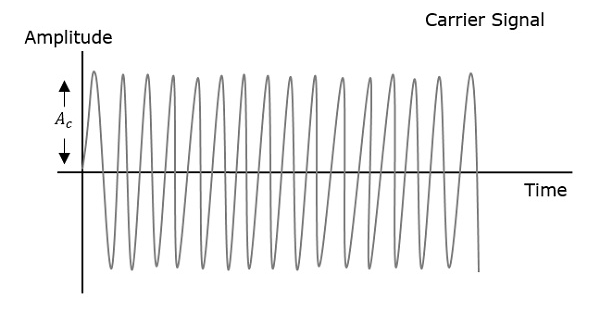
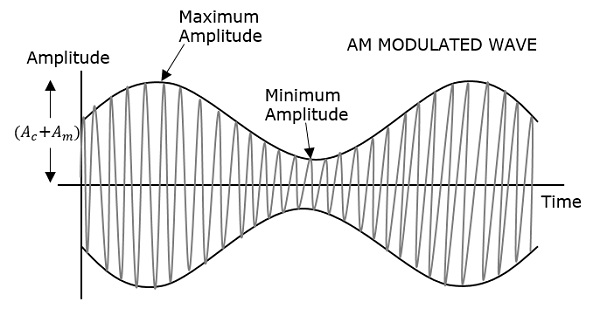
คลื่นมอดูเลตที่แสดงก่อนคือสัญญาณข้อความ อันถัดไปคือคลื่นพาหะซึ่งเป็นเพียงสัญญาณความถี่สูงและไม่มีข้อมูล ในขณะที่อันสุดท้ายคือคลื่นมอดูเลตที่เป็นผลลัพธ์

จะสังเกตได้ว่ายอดบวกและลบของคลื่นพาหะนั้นเชื่อมต่อกันด้วยเส้นสมมุติ เส้นนี้ช่วยสร้างรูปร่างที่แน่นอนของสัญญาณมอดูเลต เส้นสมมุติบนคลื่นพาหะนี้เรียกว่า asEnvelope. มันเป็นเช่นเดียวกับสัญญาณข้อความ

นิพจน์ทางคณิตศาสตร์

ต่อไปนี้เป็นนิพจน์ทางคณิตศาสตร์สำหรับคลื่นเหล่านี้

การเป็นตัวแทนโดเมนเวลาของคลื่น

ให้สัญญาณมอดูเลตเป็น -

$$ m (t) = A_mcos (2 \ pi f_mt) $$

ให้สัญญาณผู้ให้บริการ -

$$ c (t) = A_ccos (2 \ pi f_ct) $$

ที่ไหน A_m = แอมพลิจูดสูงสุดของสัญญาณมอดูเลต

A_c = แอมพลิจูดสูงสุดของสัญญาณพาหะ

รูปแบบมาตรฐานของคลื่นแอมพลิจูดมอดูเลตถูกกำหนดเป็น -

$$ S (t) = A_c [1 + K_am (t)] cos (2 \ pi f_ct) $$

$$ S (t) = A_c [1+ \ mu cos (2 \ pi f_mt)] cos (2 \ pi f_ct) $$

$$ ที่ไหน \ mu = K_aA_m $$

ดัชนีการมอดูเลต

คลื่นพาหะหลังจากถูกมอดูเลตแล้วหากคำนวณระดับมอดูเลตแล้วความพยายามดังกล่าวจะเรียกว่าเป็น Modulation Index หรือ Modulation Depth. มันระบุระดับของการมอดูเลตที่คลื่นพาหะได้รับ

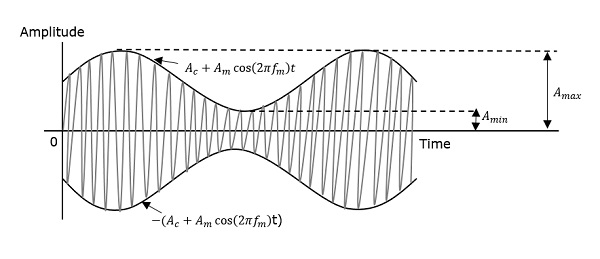
ค่าสูงสุดและต่ำสุดของซองจดหมายของคลื่นมอดูเลตจะแสดงด้วยA _maxและA _minตามลำดับ

ให้เราลองพัฒนาสมการสำหรับ Modulation Index

$$ A_ {max} = A_c (1+ \ mu) $$

เนื่องจากที่ A _{สูงสุด}ค่าของ cos θคือ 1

$$ A_ {min} = A_c (1- \ mu) $$

เนื่องจากที่ A _นาทีค่า cos θจึงเท่ากับ -1

$$ \ frac {A_ {max}} {A_ {min}} = \ frac {1+ \ mu} {1- \ mu} $$

$$ A_ {max} - \ mu A_ {max} = A_ {min} + \ mu A_ {min} $$

$$ - \ mu (A_ {max} + A_ {min}) = A_ {min} -A_ {max} $$

$$ \ mu = \ frac {A_ {max} -A_ {min}} {A_ {max} + A_ {min}} $$

ดังนั้นจึงได้สมการของ Modulation Index µหมายถึงดัชนีการมอดูเลตหรือความลึกของการมอดูเลต ซึ่งมักจะแสดงเป็นเปอร์เซ็นต์ที่เรียกว่าPercentage Modulation. เป็นขอบเขตของการมอดูเลตแสดงเป็นเปอร์เซ็นต์และแสดงด้วยm.

สำหรับการมอดูเลตที่สมบูรณ์แบบค่าของดัชนีการมอดูเลตควรเป็น 1 ซึ่งหมายความว่าความลึกของการมอดูเลตควรเป็น 100%

ตัวอย่างเช่นถ้าค่านี้น้อยกว่า 1 นั่นคือดัชนีการมอดูเลตคือ 0.5 ดังนั้นเอาต์พุตที่มอดูเลตจะมีลักษณะดังรูปต่อไปนี้ เรียกว่า Under-modulation คลื่นดังกล่าวเรียกว่าเป็นunder-modulated wave.

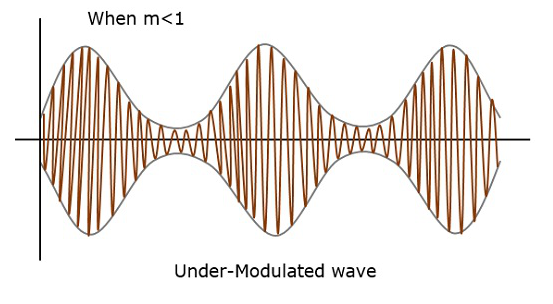
ถ้าค่าของดัชนีการมอดูเลตมากกว่า 1 เช่น 1.5 หรือมากกว่านั้นคลื่นจะเป็น over-modulated wave. จะมีลักษณะดังรูปต่อไปนี้

เมื่อค่าดัชนีการมอดูเลตเพิ่มขึ้นผู้ให้บริการจะประสบกับการกลับเฟส 180 °ซึ่งทำให้เกิดแถบด้านข้างเพิ่มเติมและด้วยเหตุนี้คลื่นจึงบิดเบี้ยว คลื่นที่มีการมอดูเลตมากเกินไปทำให้เกิดการรบกวนซึ่งไม่สามารถกำจัดได้