Python - ประเภทอัลกอริทึม

ต้องวิเคราะห์ประสิทธิภาพและความแม่นยำของอัลกอริทึมเพื่อเปรียบเทียบและเลือกอัลกอริทึมเฉพาะสำหรับสถานการณ์บางอย่าง กระบวนการวิเคราะห์นี้เรียกว่า Asymptotic analysis หมายถึงการคำนวณเวลาทำงานของการดำเนินการใด ๆ ในหน่วยคำนวณทางคณิตศาสตร์ ตัวอย่างเช่นเวลาทำงานของการดำเนินการหนึ่งคำนวณเป็น f (n) และอาจเป็นสำหรับการดำเนินการอื่นที่คำนวณเป็น g (n2) ซึ่งหมายความว่าเวลาทำงานของการดำเนินการครั้งแรกจะเพิ่มขึ้นในเชิงเส้นเมื่อเพิ่มขึ้นของ n และเวลาทำงานของการดำเนินการที่สองจะเพิ่มขึ้นแบบทวีคูณเมื่อ n เพิ่มขึ้น ในทำนองเดียวกันเวลาทำงานของการดำเนินการทั้งสองจะใกล้เคียงกันถ้า n มีขนาดเล็กมาก

โดยปกติเวลาที่อัลกอริทึมต้องการจะอยู่ภายใต้สามประเภท -

กรณีที่ดีที่สุด - เวลาขั้นต่ำที่จำเป็นสำหรับการทำงานของโปรแกรม
Average Case - เวลาเฉลี่ยที่จำเป็นสำหรับการทำงานของโปรแกรม
กรณีที่เลวร้ายที่สุด - เวลาสูงสุดที่จำเป็นสำหรับการเรียกใช้โปรแกรม

สัญกรณ์ Asymptotic

ต่อไปนี้เป็นสัญกรณ์ asymptotic ที่ใช้กันทั่วไปในการคำนวณความซับซ้อนของเวลาทำงานของอัลกอริทึม

Οสัญกรณ์
Ωสัญกรณ์
θสัญกรณ์

สัญกรณ์ Big Oh, Ο

สัญกรณ์Ο (n) เป็นวิธีที่เป็นทางการในการแสดงขอบเขตบนของเวลาทำงานของอัลกอริทึม เป็นการวัดความซับซ้อนของเวลากรณีที่เลวร้ายที่สุดหรือระยะเวลาที่ยาวนานที่สุดที่อัลกอริทึมอาจใช้เพื่อทำให้เสร็จสมบูรณ์

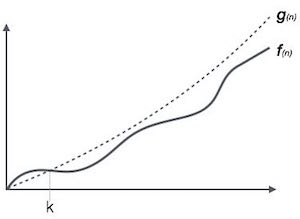
ตัวอย่างเช่นสำหรับฟังก์ชัน f(n)

Ο(f(n)) = { g(n) : there exists c > 0 and n₀ such that f(n) ≤ c.g(n) for all n > n₀. }

สัญกรณ์ Omega, Ω

สัญกรณ์Ω (n) เป็นวิธีที่เป็นทางการในการแสดงขอบเขตล่างของเวลาทำงานของอัลกอริทึม เป็นการวัดความซับซ้อนของเวลากรณีและปัญหาที่ดีที่สุดหรือระยะเวลาที่ดีที่สุดที่อัลกอริทึมสามารถใช้เพื่อทำให้เสร็จสมบูรณ์

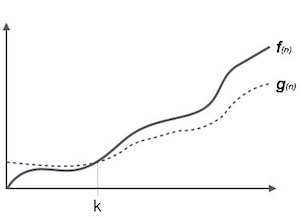
ตัวอย่างเช่นสำหรับฟังก์ชัน f(n)

Ω(f(n)) ≥ { g(n) : there exists c > 0 and n₀ such that g(n) ≤ c.f(n) for all n > n₀. }

สัญลักษณ์ Theta, θ

สัญกรณ์θ (n) เป็นวิธีที่เป็นทางการในการแสดงทั้งขอบเขตล่างและขอบเขตบนของเวลาทำงานของอัลกอริทึม แสดงเป็นดังนี้ -

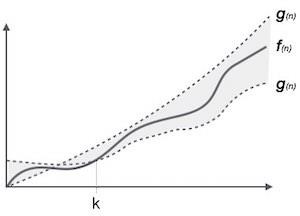
θ(f(n)) = { g(n) if and only if g(n) =  Ο(f(n)) and g(n) = Ω(f(n)) for all n > n₀. }

สัญกรณ์ Asymptotic ทั่วไป

ต่อไปนี้เป็นรายการสัญกรณ์ asymptotic ทั่วไป -

คงที่	-	Ο (1)
ลอการิทึม	-	Ο (บันทึก n)
เชิงเส้น	-	Ο (n)
n log n	-	Ο (n บันทึก n)
กำลังสอง	-	Ο (n ² )
ลูกบาศก์	-	Ο (n ³ )
พหุนาม	-	n ^{Ο (1)}
เลขชี้กำลัง	-	2 ^{Ο (น)}