การสื่อสารผ่านดาวเทียม - กลศาสตร์การโคจร

เรารู้ว่าเส้นทางของดาวเทียมที่หมุนรอบโลกเป็นที่รู้จักกันในชื่อ orbit. เส้นทางนี้สามารถแสดงด้วยสัญกรณ์ทางคณิตศาสตร์ กลศาสตร์การโคจรคือการศึกษาการเคลื่อนที่ของดาวเทียมที่มีอยู่ในวงโคจร ดังนั้นเราจึงสามารถเข้าใจการทำงานของอวกาศได้อย่างง่ายดายด้วยความรู้เกี่ยวกับการเคลื่อนที่ของวงโคจร

องค์ประกอบวงโคจร

องค์ประกอบของวงโคจรเป็นพารามิเตอร์ซึ่งมีประโยชน์ในการอธิบายการเคลื่อนที่ของวงโคจรของดาวเทียม ต่อไปนี้คือไฟล์orbital elements.

แกนกึ่งหลัก
Eccentricity
หมายถึงความผิดปกติ
อาร์กิวเมนต์ของ perigee
Inclination
การขึ้นไปทางขวาของโหนดจากน้อยไปมาก

องค์ประกอบวงโคจรทั้งหกข้างต้นกำหนดวงโคจรของดาวเทียมโลก ดังนั้นจึงเป็นเรื่องง่ายที่จะแยกแยะดาวเทียมดวงหนึ่งจากดาวเทียมดวงอื่นโดยพิจารณาจากค่าขององค์ประกอบวงโคจร

แกนกึ่งหลัก

ความยาวของ Semi-major axis (a)กำหนดขนาดของวงโคจรของดาวเทียม มันเป็นครึ่งหนึ่งของแกนหลัก สิ่งนี้จะวิ่งจากจุดศูนย์กลางผ่านโฟกัสไปที่ขอบของวงรี ดังนั้นมันจึงเป็นรัศมีของวงโคจรที่สองจุดที่ไกลที่สุดของวงโคจร

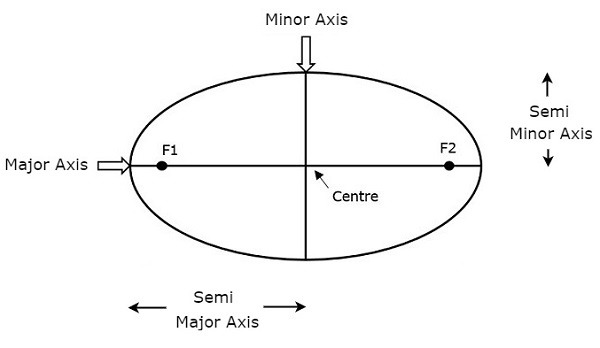
ทั้งแกนกึ่งหลักและกึ่งรองจะแสดงในรูปด้านบน ความยาวกึ่งmajor axis (a) ไม่เพียง แต่กำหนดขนาดวงโคจรของดาวเทียมเท่านั้น แต่ยังรวมถึงช่วงเวลาแห่งการปฏิวัติด้วย

ถ้าวงโคจรวงกลมถือเป็นกรณีพิเศษความยาวของแกนกึ่งสำคัญจะเท่ากับ radius ของวงโคจรวงกลมนั้น

ความเยื้องศูนย์

คุณค่าของ Eccentricity (e)แก้ไขรูปร่างของวงโคจรของดาวเทียม พารามิเตอร์นี้บ่งชี้ความเบี่ยงเบนของรูปร่างของวงโคจรจากวงกลมที่สมบูรณ์แบบ

ถ้าความยาวของแกนกึ่งหลักและแกนรองกึ่งเล็กของวงโคจรรูปไข่เป็น a & b ดังนั้นนิพจน์ทางคณิตศาสตร์สำหรับ eccentricity (e) จะ

$$ e = \ frac {\ sqrt {a ^ 2 - b ^ 2}} {a} $$

ค่าของความเยื้องศูนย์ของวงโคจรวงกลมคือ zeroเนื่องจากทั้ง a & b เท่ากัน ในขณะที่ค่าของความเยื้องศูนย์ของวงโคจรรูปไข่อยู่ระหว่างศูนย์ถึงหนึ่ง

ดังต่อไปนี้ figure แสดงวงโคจรของดาวเทียมต่างๆสำหรับค่าความเยื้องศูนย์ (e) ที่แตกต่างกัน

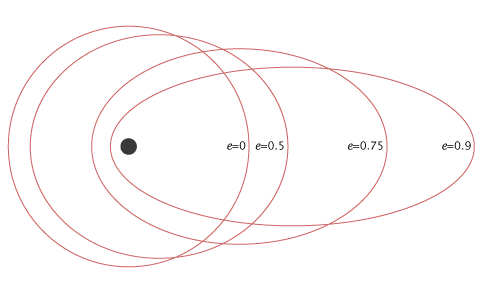
จากรูปด้านบนวงโคจรของดาวเทียมที่สอดคล้องกับค่าความเยื้องศูนย์ (e) ของศูนย์คือวงโคจรวงกลม และวงโคจรของดาวเทียมอีกสามดวงที่เหลือเป็นวงรีที่สอดคล้องกับค่าความเบี้ยว (e) 0.5, 0.75 และ 0.9

หมายถึงความผิดปกติ

สำหรับดาวเทียมจุดที่อยู่ใกล้โลกมากที่สุดเรียกว่า Perigee Mean anomaly (M) ให้ค่าเฉลี่ยของตำแหน่งเชิงมุมของดาวเทียมโดยอ้างอิงถึง perigee

ถ้าวงโคจรเป็นวงกลมความผิดปกติค่าเฉลี่ยจะให้ตำแหน่งเชิงมุมของดาวเทียมในวงโคจร แต่ถ้าวงโคจรเป็นวงรีการคำนวณตำแหน่งที่แน่นอนนั้นยากมาก ในขณะนั้นค่าเฉลี่ยความผิดปกติจะใช้เป็นขั้นตอนกลาง

อาร์กิวเมนต์ของ Perigee

วงโคจรของดาวเทียมตัดระนาบเส้นศูนย์สูตรสองจุด จุดแรกเรียกว่าdescending nodeซึ่งดาวเทียมเคลื่อนผ่านจากซีกโลกเหนือไปยังซีกโลกใต้ จุดที่สองเรียกว่าascending nodeซึ่งดาวเทียมเคลื่อนผ่านจากซีกโลกใต้ไปยังซีกโลกเหนือ

Argument of perigee (ω)คือมุมระหว่างโหนดจากน้อยไปมากและ perigee ถ้าทั้ง perigee และโหนดจากน้อยไปมากมีอยู่ในจุดเดียวกันอาร์กิวเมนต์ของ perigee จะเป็นศูนย์องศา

อาร์กิวเมนต์ของ perigee วัดได้ในระนาบวงโคจรที่ศูนย์กลางของโลกตามทิศทางการเคลื่อนที่ของดาวเทียม

ความโน้มเอียง

มุมระหว่างระนาบวงโคจรกับระนาบเส้นศูนย์สูตรของโลกเรียกว่า inclination (i). วัดจากโหนดจากน้อยไปมากโดยมีทิศทางเป็นตะวันออกไปเหนือ ดังนั้นการเอียงจึงกำหนดแนวของวงโคจรโดยพิจารณาจากเส้นศูนย์สูตรของโลกเป็นข้อมูลอ้างอิง

มีสี่ประเภทของวงโคจรตามมุมเอียง

Equatorial orbit - มุมเอียงเป็นศูนย์องศาหรือ 180 องศา
Polar orbit - มุมเอียง 90 องศา
Prograde orbit - มุมเอียงอยู่ระหว่างศูนย์ถึง 90 องศา
Retrograde orbit - มุมเอียงอยู่ระหว่าง 90 ถึง 180 องศา

การขึ้นไปทางขวาของโหนดจากน้อยไปมาก

เรารู้ว่า ascending node คือจุดที่ดาวเทียมพาดผ่านระนาบเส้นศูนย์สูตรขณะเคลื่อนจากซีกโลกใต้ไปยังซีกโลกเหนือ

การขึ้นไปทางขวาของโหนดจากน้อยไปหามาก (Ω)คือมุมระหว่างเส้นของราศีเมษและโหนขึ้นไปทางทิศตะวันออกในระนาบเส้นศูนย์สูตร ราศีเมษเรียกอีกอย่างว่า vernal และ equinox

ดาวเทียม ground trackคือเส้นทางบนพื้นผิวโลกซึ่งอยู่ใต้วงโคจรของมัน การติดตามพื้นของดาวเทียมอาจมีหลายรูปแบบขึ้นอยู่กับค่าขององค์ประกอบการโคจร

สมการการโคจร

ในส่วนนี้ให้เราพูดคุยเกี่ยวกับสมการที่เกี่ยวข้องกับการเคลื่อนที่ของวงโคจร

กองกำลังที่ทำหน้าที่บนดาวเทียม

ดาวเทียมเมื่อหมุนรอบโลกจะได้รับแรงดึงจากโลกเนื่องจากแรงโน้มถ่วงของโลก กองกำลังนี้เรียกว่าCentripetal force(F ₁ ) เนื่องจากแรงนี้ทำให้ดาวเทียมพุ่งเข้าหามัน

ในทางคณิตศาสตร์ Centripetal force(F ₁ ) ที่ทำหน้าที่บนดาวเทียมเนื่องจากพื้นโลกสามารถเขียนเป็น

$$ F_ {1} = \ frac {GMm} {R ^ 2} $$

ที่ไหน

Gเป็นสากลอย่างต่อเนื่องแรงโน้มถ่วงและมันจะมีค่าเท่ากับ 6.673 x 10 ^-11 N ∙ม. ² / กก. 2
Mคือมวลของโลกและเท่ากับ 5.98 x 10 ²⁴ Kg.
m คือมวลของดาวเทียม
R คือระยะทางจากดาวเทียมถึงศูนย์กลางของโลก

ดาวเทียมเมื่อหมุนรอบโลกจะได้รับแรงดึงจากดวงอาทิตย์และดวงจันทร์เนื่องจากแรงดึงดูดของโลก กองกำลังนี้เรียกว่าCentrifugal force(F ₂ ) เนื่องจากแรงนี้ทำให้ดาวเทียมอยู่ห่างจากพื้นโลก

ในทางคณิตศาสตร์ Centrifugal force(F ₂ ) ที่แสดงบนดาวเทียมสามารถเขียนเป็น

$$ F_ {2} = \ frac {mv ^ 2} {R} $$

ที่ไหน v คือความเร็วในการโคจรของดาวเทียม

ความเร็ววงโคจร

ความเร็วในการโคจรของดาวเทียมคือความเร็วที่ดาวเทียมหมุนรอบโลก ดาวเทียมไม่เบี่ยงเบนไปจากวงโคจรและเคลื่อนที่ด้วยความเร็วที่แน่นอนในวงโคจรนั้นเมื่อทั้งแรงสู่ศูนย์กลางและแรงเหวี่ยงbalance ซึ่งกันและกัน

ดังนั้น, equateแรงสู่ศูนย์กลาง (F ₁ ) และแรงเหวี่ยง (F ₂ )

$$ \ frac {GMm} {R ^ 2} = \ frac {mv ^ 2} {R} $$

$$ => \ frac {GM} {R} = v ^ 2 $$

$$ => v = \ sqrt {\ frac {GM} {R}} $$

ดังนั้นไฟล์ orbital velocity ของดาวเทียมคือ

$$ v = \ sqrt {\ frac {GM} {R}} $$

ที่ไหน