Elektronik Devreler - Sinyaller
Bir Signal"Üretildiği kaynakta bulunan veriler hakkında bazı bilgiler veren bir temsil" olarak anlaşılabilir. Bu genellikle zamanla değişir. Bu nedenle, bir sinyal birsource of energy which transmits some information. Bu, bir grafik üzerinde kolaylıkla gösterilebilir.
Örnekler
- Alarm, zamanın geldiğine dair bir sinyal verir.
- Bir ocak düdüğü, yemeğin piştiğini doğrular.
- Kırmızı ışık bazı tehlikelere işaret eder.
- Trafik sinyali hareket ettiğinizi gösterir.
- Sizin için bir çağrı sinyali veren bir telefon çalar.
Bir sinyal, bazı bilgileri ileten herhangi bir türde olabilir. Elektronik bir ekipmandan üretilen bu sinyale,Electronic Signal veya Electrical Signal. Bunlar genellikle zaman değişkenleridir.
Sinyal Türleri
Sinyaller, özelliklerine bağlı olarak Analog veya Dijital olarak sınıflandırılabilir. Aşağıdaki resimde gösterildiği gibi, Analog ve Dijital sinyaller ayrıca sınıflandırılabilir.
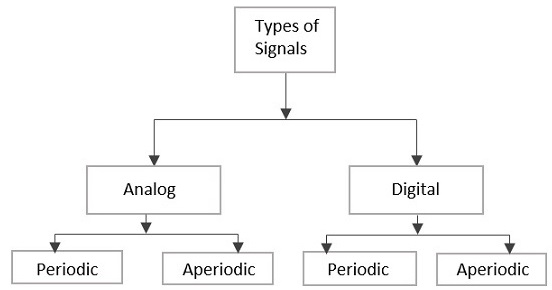
Analog Sinyal
Zamanla değişen bir miktarı temsil eden sürekli, zamanla değişen bir sinyal, bir Analog Signal. Bu sinyal, kendisini temsil eden miktarın anlık değerlerine göre zamana göre değişmeye devam eder.
Dijital sinyal
Olan bir sinyal discrete doğada veya hangisi non-continuous formda olarak adlandırılabilir Digital signal. Bu sinyalin, sanki belirli bir anda türetilmiş gibi, önceki değerlere dayanmayan ayrı ayrı gösterilen ayrı değerleri vardır.
Periyodik Sinyal ve Periyodik Sinyal
Modelini belirli bir süre boyunca tekrarlayan herhangi bir analog veya dijital sinyale, Periodic Signal. Bu sinyalin deseni tekrar tekrar devam ettirilir ve varsayılması veya hesaplanması kolaydır.
Modelini belirli bir süre boyunca tekrar etmeyen herhangi bir analog veya dijital sinyale, Aperiodic Signal. Bu sinyalin paterni devam ettirilir, ancak model tekrarlanmaz ve varsayılması veya hesaplanması o kadar kolay değildir.
Sinyaller ve Gösterimler
Arasında Periodic SignalsEn sık kullanılan sinyaller Sinüs dalgası, Kosinüs dalgası, Üçgen dalga formu, Kare dalga, Dikdörtgen dalga, Testere dişi dalga formu, Darbe dalga şekli veya darbe katarı vb. dalga formlarına bir göz atalım.
Birim Adım Sinyali
Birim adım sinyali, başlangıç noktasından X ekseni üzerindeki bir birime kadar bir birim değerine sahiptir. Bu çoğunlukla bir test sinyali olarak kullanılır. Birim adım sinyalinin görüntüsü aşağıda gösterilmiştir.
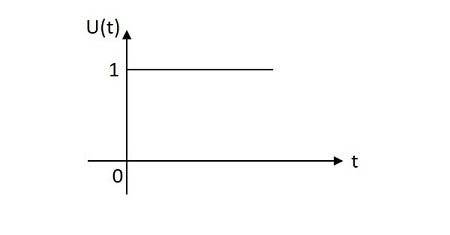
Birim adım işlevi $ u \ left (t \ right) $ ile gösterilir. Şu şekilde tanımlanır -
$$ u \ left (t \ right) = \ left \ {\ begin {matrix} 1 & t \ geq 0 \\ 0 & t <0 \ end {matrix} \ right. $$
Birim Darbe Sinyali
Birim dürtü sinyali, başlangıç noktasında bir birim değerine sahiptir. Alanı bir birimdir. Birim dürtü sinyalinin görüntüsü aşağıda gösterilmiştir.
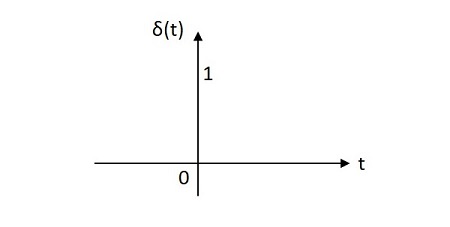
Birim dürtü işlevi şu şekilde gösterilir: ẟ(t). Olarak tanımlanır
$$ \ delta \ left (t \ right) = \ left \ {\ begin {matrix} \ infty \: \: if \: \: t = 0 \\ 0 \: \: if \: \: t \ neq 0 \ end {matrix} \ right. $$
$$ \ int _ {- \ infty} ^ {\ infty} \ delta \ left (t \ right) d \ left (t \ sağ) = 1 $$
$$ \ int _ {- \ infty} ^ {t} \ delta \ left (t \ sağ) d \ left (t \ sağ) = u \ sol (t \ sağ) $$
$$ \ delta \ left (t \ sağ) = \ frac {du \ left (t \ sağ)} {d \ left (t \ sağ)} $$
Birim Rampa Sinyali
Birim rampa sinyalinin değeri, kaynağından üssel olarak artan bir değere sahiptir. Birim rampa sinyalinin görüntüsü aşağıda gösterilmiştir.
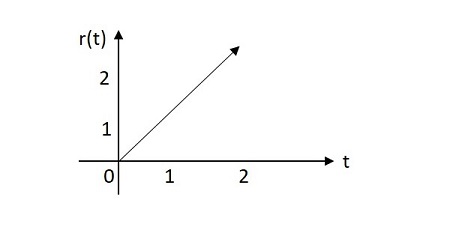
Birim rampa işlevi şu şekilde gösterilir: u(t). Şu şekilde tanımlanır -
$$ \ int_ {0} ^ {t} u \ left (t \ right) d \ left (t \ right) = \ int_ {0} ^ {t} 1 dt = t = r \ left (t \ sağ) $$
$$ u \ left (t \ right) = \ frac {dr \ left (t \ right)} {dt} $$
Birim Parabolik Sinyal
Birim parabolik sinyalin değeri, kaynağında bir parabol gibi değişen değerlere sahiptir. Birim parabolik sinyalin görüntüsü aşağıda gösterilmiştir.
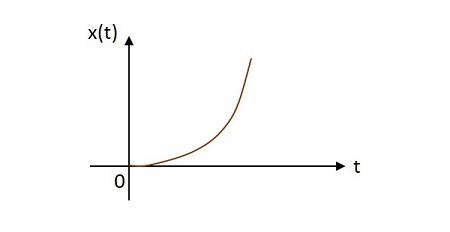
Birim parabolik işlevi $ u \ left (t \ right) $ ile gösterilir. Şu şekilde tanımlanır -
$$ \ int_ {0} ^ {t} \ int_ {0} ^ {t} u \ left (t \ right) dtdt = \ int_ {0} ^ {t} r \ left (t \ right) dt = \ int_ {0} ^ {t} t.dt = \ frac {t ^ {2}} {2} dt = x \ left (t \ right) $$
$$ r \ left (t \ right) = \ frac {dx \ left (t \ right)} {dt} $$
$$ u \ left (t \ right) = \ frac {d ^ {2} x \ left (t \ right)} {dt ^ {2}} $$
Signum İşlevi
Signum işlevinin değeri, başlangıcından itibaren hem pozitif hem de negatif düzlemlerde eşit olarak dağıtılmıştır. Signum işlevinin görüntüsü aşağıda gösterilmiştir.
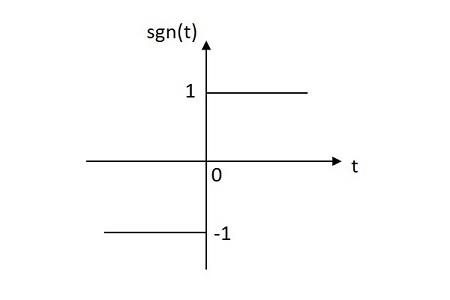
Signum işlevi şu şekilde gösterilir: sgn(t). Olarak tanımlanır
$$ sgn \ left (t \ right) = \ left \ {\ begin {matrix} 1 \: \: for \: \: t \ geq 0 \\ - 1 \: \: for \: \: t <0 \ end {matris} \ sağ. $$
$$ sgn \ left (t \ right) = 2u \ left (t \ sağ) -1 $$
Üstel Sinyal
Üstel sinyalin değeri, kaynağından üssel olarak farklılaşmaktadır. Üstel fonksiyon şu şekildedir -
$$ x \ left (t \ sağ) = e ^ {\ alpha t} $$
Üstel biçim, $ \ alpha $ ile tanımlanabilir. Bu işlev 3 durumda anlaşılabilir
Case 1 -
$ \ Alpha = 0 \ rightarrow x \ left (t \ right) = e ^ {0} = 1 $ ise
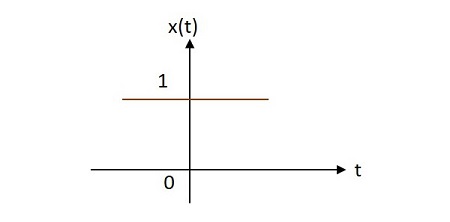
Case 2 -
$ \ Alpha <0 $ ise $ x \ left (t \ right) = e ^ {\ alpha t} $ burada $ \ alpha $ negatiftir. Bu şekledecaying exponential.
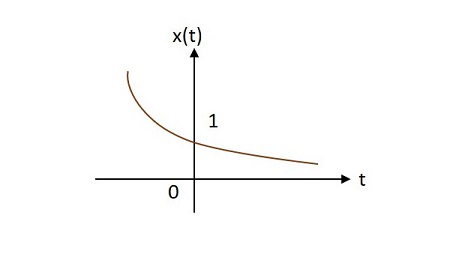
Case 3 -
$ \ Alpha> 0 $ ise $ x \ left (t \ right) = e ^ {\ alpha t} $ burada $ \ alpha $ pozitiftir. Bu şekleraising exponential.
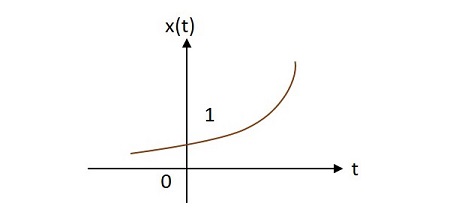
Dikdörtgen Sinyal
Dikdörtgen sinyal, kaynağından hem pozitif hem de negatif düzlemlerde dikdörtgen şeklinde dağıtılmış değerine sahiptir. Dikdörtgen sinyal görüntüsü aşağıda gösterilmiştir.
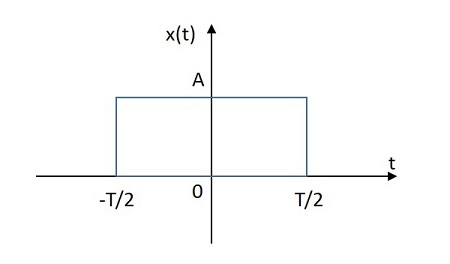
Dikdörtgen fonksiyon $ x \ left (t \ right) $ ile gösterilir. Olarak tanımlanır
$$ x \ left (t \ right) = A \: rect \ left [\ frac {t} {T} \ right] $$
Üçgen Sinyal
Dikdörtgen sinyalin değeri, kaynağından itibaren hem pozitif hem de negatif düzlemlerde üçgen şeklinde dağıtılmıştır. Üçgen sinyalin görüntüsü aşağıda gösterilmiştir.
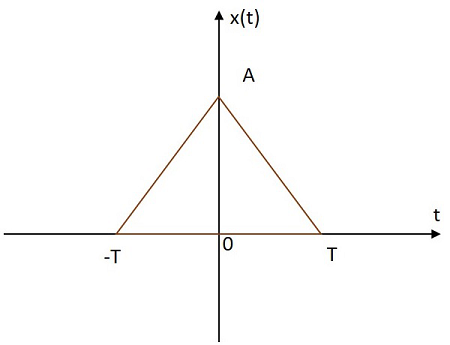
Üçgen işlev $ x \ left (t \ right) $ ile gösterilir. Olarak tanımlanır
$$ x \ left (t \ sağ) = A \ sol [1- \ frac {\ sol | t \ right |} {T} \ right] $$
Sinüzoidal Sinyal
Sinüzoidal sinyalin değeri, kaynağından sinüzoidal olarak değişir. Sinüzoidal sinyalin görüntüsü aşağıda gösterilmiştir.
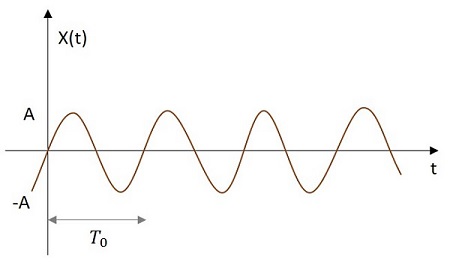
Sinüzoidal fonksiyon x (t) ile gösterilir. Şu şekilde tanımlanır -
$$ x \ left (t \ sağ) = A \ cos \ left (w_ {0} t \ pm \ phi \ right) $$
veya
$$ x \ left (t \ sağ) = Bir günah \ sol (w_ {0} t \ pm \ phi \ sağ) $$
$ T_ {0} = \ frac {2 \ pi} {w_ {0}} $ nerede
Sinc İşlevi
Sinc sinyalinin değeri, aşağıda verilen denklemde olduğu gibi belirli bir ilişkiye göre değişir. Başlangıç noktasında maksimum değerine sahiptir ve uzaklaştıkça azalmaya devam eder. Bir Sinc işlevi sinyalinin görüntüsü aşağıda gösterilmiştir.
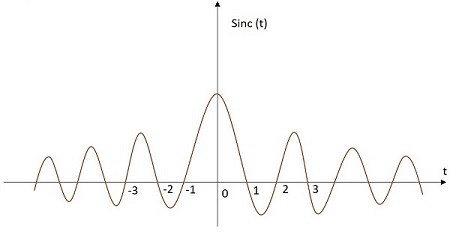
Sinc işlevi şu şekilde gösterilir: sinc(t). Şu şekilde tanımlanır -
$$ sinc \ left (t \ sağ) = \ frac {sin \ left (\ pi t \ sağ)} {\ pi t} $$
İşte bunlar Elektronik ve İletişim alanında en çok karşılaştığımız farklı sinyaller. Sinyal analizini kolaylaştırmak için her sinyal matematiksel bir denklemde tanımlanabilir.
Her sinyal, daha önce bahsedildiği gibi belirli bir dalga şekline sahiptir. Dalganın şekillendirilmesi, sinyalde bulunan içeriği değiştirebilir. Her neyse, belirli bir devre için bir dalganın değiştirilip değiştirilmeyeceği tasarım mühendisi tarafından verilecek bir karardır. Ancak, dalganın şeklini değiştirmek için, daha sonraki birimlerde tartışılacak birkaç teknik vardır.