LPF ve HPF'nin Özel Fonksiyonları

Alçak geçiren ve yüksek geçiren filtre devreleri birçok uygulamada özel devreler olarak kullanılır. Alçak geçiren filtre (LPF) birIntegratoryüksek geçiren filtre (HPF) ise bir Differentiator. Bu iki matematiksel fonksiyon ancak bir elektronik mühendisinin birçok uygulamadaki çabasını azaltan bu devrelerle mümkündür.

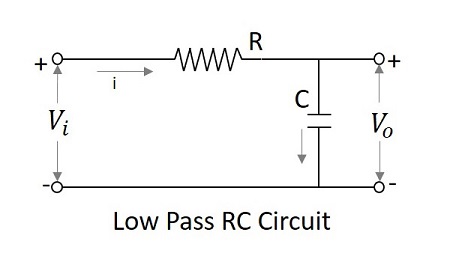
Entegratör Olarak Düşük Geçişli Filtre

Düşük frekanslarda, kapasitif reaktans sonsuz olma eğilimindedir ve yüksek frekanslarda reaktans sıfır olur. Bu nedenle, düşük frekanslarda, LPF sonlu çıkışa sahiptir ve yüksek frekanslarda çıkış sıfırdır, bu da bir entegratör devresi için aynıdır. Bu nedenle alçak geçiren filtrenin birintegrator.

LPF'nin entegratör olarak davranması için

$$ \ tau \ gg T $$

$ \ Tau = RC $ ise devrenin zaman sabiti

O zaman C'deki voltaj değişimi çok küçüktür.

$$ V_ {i} = iR + \ frac {1} {C} \ int i \: dt $$

$$ V_ {i} \ cong iR $$

$$ \: \: \ frac {1} {C} \ int i \: dt \ ll iR $$ tarihinden itibaren

$$ i = \ frac {V_ {i}} {R} $$

$$ \: \: V_ {0} = \ frac {1} {C} \ int i dt = \ frac {1} {RC} \ int V_ {i} dt = \ frac {1} {\ tau} 'dan beri \ int V_ {i} dt $$

$$ Output \ propto \ int input $$

Bu nedenle, büyük zaman sabitine sahip bir LPF, bir girişin integrali ile orantılı bir çıktı üretir.

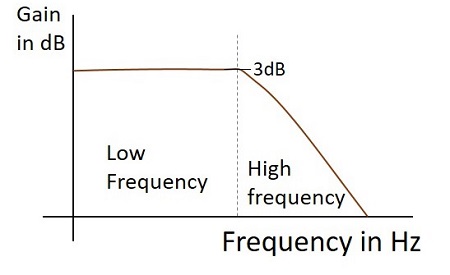
Frekans tepkisi

Entegratör olarak çalışırken pratik bir alçak geçiren filtrenin Frekans tepkisi aşağıda gösterildiği gibidir.

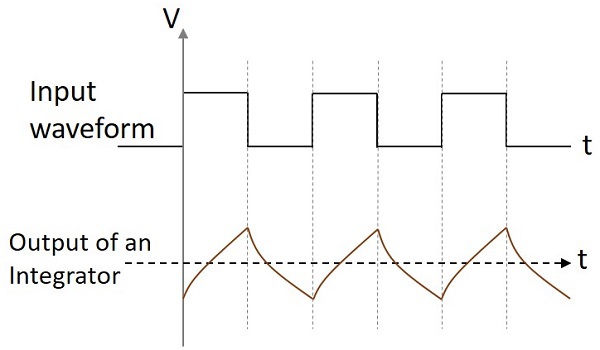
Çıkış Dalga Formu

Entegratör devresine bir sinüs dalgası girişi verilirse, çıkış bir kosinüs dalgası olacaktır. Giriş bir kare dalga ise, çıkış dalga formu şeklini değiştirir ve aşağıdaki şekilde görüldüğü gibi görünür.

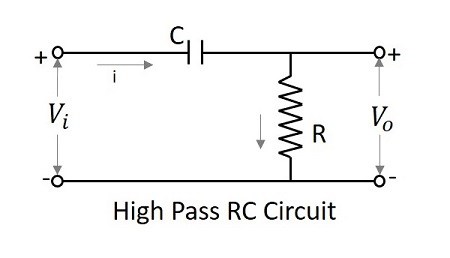
Farklılaştırıcı Olarak Yüksek Geçişli Filtre

Düşük frekanslarda, bir farklılaştırıcının çıkışı sıfır iken, yüksek frekanslarda çıkışı bazı sonlu değerdedir. Bu, farklılaştırıcı ile aynıdır. Bu nedenle, yüksek geçiş filtresinin bir farklılaştırıcı olarak davrandığı söylenir.

RC HPF'nin zaman sabiti, giriş sinyalinin zaman periyodundan çok daha küçükse, devre bir farklılaştırıcı olarak davranır. Daha sonra, R üzerindeki voltaj düşüşü, C'deki düşüşle karşılaştırıldığında çok küçüktür.

$$ V_ {i} = \ frac {1} {C} \ int i \: dt + iR $$

Ama $ iR = V_ {0} $ küçük

$$ V_ {i} = \ frac {1} {C} \ int i \: dt $$ tarihinden beri

$$ i = \ frac {V_ {0}} {R} $$

$$ \: V_ {i} = \ frac {1} {\ tau} \ int V_ {0} \: dt $$ tarihinden beri

$ \ Tau = RC $ ise devrenin zaman sabiti.

Her iki tarafta da farklılaşan,

$$ \ frac {dV_ {i}} {dt} = \ frac {V_0} {\ tau} $$

$$ V_ {0} = \ tau \ frac {dV_ {i}} {dt} $$

$$ \: V_ {0} \ propto \ frac {dV_ {i}} {dt} $$ tarihinden itibaren

Çıkış, giriş sinyalinin diferansiyeliyle orantılıdır.

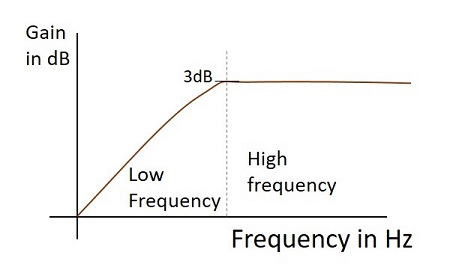
Frekans tepkisi

Farklılaştırıcı olarak çalışırken pratik bir yüksek geçiren filtrenin Frekans tepkisi aşağıda gösterildiği gibidir.

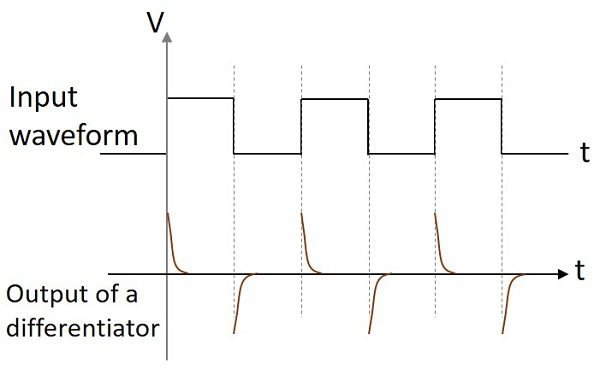
Çıkış Dalga formu

Farklılaştırıcı devresine bir sinüs dalgası girişi verilirse, çıkış bir kosinüs dalgası olacaktır. Giriş bir kare dalga ise, çıkış dalga formu şeklini değiştirir ve aşağıdaki şekilde görüldüğü gibi görünür.

Bu iki devre çoğunlukla çeşitli elektronik uygulamalarda kullanılır. Bir farklılaştırıcı devresi, uygulanan giriş sürekli olarak değişme eğiliminde olduğunda sabit bir çıkış voltajı üretir. Bir entegratör devresi, uygulanan giriş voltajı sabit olduğunda sürekli değişen bir çıkış voltajı üretir.