MATLAB - Matematik

MATLAB, diferansiyel ve integral analiz problemlerini çözmek, herhangi bir derecedeki diferansiyel denklemleri çözmek ve limitleri hesaplamak için çeşitli yollar sunar. Hepsinden iyisi, karmaşık fonksiyonların grafiklerini kolayca çizebilir ve orijinal fonksiyonun yanı sıra türevini de çözerek bir grafik üzerinde maksimum, minimum ve diğer kırtasiye noktalarını kontrol edebilirsiniz.

Bu bölüm kalkülüs problemlerini ele alacaktır. Bu bölümde, analiz öncesi kavramları, yani fonksiyonların limitlerini hesaplamayı ve limit özelliklerini doğrulamayı tartışacağız.

Bir sonraki bölümde Diferansiyel , bir ifadenin türevini hesaplayacağız ve bir grafikte yerel maksimum ve minimumları bulacağız. Ayrıca diferansiyel denklemleri çözmeyi de tartışacağız.

Son olarak, Entegrasyon bölümünde integral hesabını tartışacağız.

Limitlerin Hesaplanması

MATLAB, limitlimitleri hesaplama işlevi. En temel haliyle,limit fonksiyon ifadeyi argüman olarak alır ve bağımsız değişken sıfıra giderken ifadenin sınırını bulur.

Örneğin, x sıfıra yönelirken f (x) = (x ³ + 5) / (x ⁴ + 7) fonksiyonunun sınırını hesaplayalım .

syms x
limit((x^3 + 5)/(x^4 + 7))

MATLAB yukarıdaki ifadeyi çalıştıracak ve aşağıdaki sonucu döndürecektir -

ans =
   5/7

Limit işlevi sembolik hesaplama alanına girer; kullanmanız gerekiyorsymsMATLAB'a hangi sembolik değişkenleri kullandığınızı söyleyen işlev. Değişken sıfırdan farklı bir sayıya yöneldiğinden, bir işlevin sınırını da hesaplayabilirsiniz. Lim _{x-> a} (f (x)) hesaplamak için, limit komutunu argümanlarla birlikte kullanırız. Birincisi ifade ve ikincisi x'in yaklaştığı sayıdır, işte a .

Örneğin, x 1'e meylederken f (x) = (x-3) / (x-1) fonksiyonunun sınırını hesaplayalım.

limit((x - 3)/(x-1),1)

MATLAB yukarıdaki ifadeyi çalıştıracak ve aşağıdaki sonucu döndürecektir -

ans =
   NaN

Başka bir örnek alalım,

limit(x^2 + 5, 3)

MATLAB yukarıdaki ifadeyi çalıştıracak ve aşağıdaki sonucu döndürecektir -

ans =
   14

Octave Kullanarak Limitleri Hesaplama

Aşağıdakiler kullanılarak yukarıdaki örneğin Oktav versiyonu symbolic paketi çalıştırmayı ve sonucu karşılaştırmayı deneyin -

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Octave yukarıdaki ifadeyi çalıştıracak ve aşağıdaki sonucu döndürecektir -

ans =
   0.7142857142857142857

Limitlerin Temel Özelliklerinin Doğrulanması

Cebirsel Limit Teoremi, limitlerin bazı temel özelliklerini sağlar. Bunlar aşağıdaki gibidir -

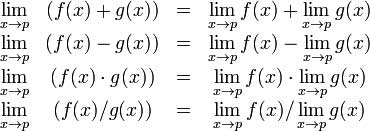
İki işlevi ele alalım -

f (x) = (3x + 5) / (x - 3)
g (x) = x ² + 1.

Her iki fonksiyonun da x'in 5'e meyilli olarak fonksiyonların limitlerini hesaplayalım ve bu iki fonksiyonu ve MATLAB'ı kullanarak limitlerin temel özelliklerini doğrulayalım.

Misal

Bir komut dosyası oluşturun ve aşağıdaki kodu içine yazın -

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

Dosyayı çalıştırdığınızda, -

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

Octave Kullanarak Limitlerin Temel Özelliklerinin Doğrulanması

Aşağıdakiler kullanılarak yukarıdaki örneğin Oktav versiyonu symbolic paketi çalıştırmayı ve sonucu karşılaştırmayı deneyin -

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Octave yukarıdaki ifadeyi çalıştıracak ve aşağıdaki sonucu döndürecektir -

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

Sol ve Sağ Taraf Sınırları

Bir fonksiyon değişkenin belirli bir değeri için süreksizliğe sahipse, limit o noktada mevcut değildir. Başka bir deyişle, bir f (x) fonksiyonunun limitleri, x = a'da süreksizliğe sahiptir; limit değeri, x sol taraftan x'e yaklaştığında, x sağ taraftan yaklaştıkça limit değerine eşit değildir.

Bu, solak ve sağ elini kullanan sınırlar kavramına götürür. Solak bir sınır, soldan x -> a olarak sınır olarak tanımlanır, yani x <a değerleri için x, a'ya yaklaşır. Sağ elini kullanan bir sınır, sınır olarak sağdan x -> a olarak tanımlanır, yani x> a değerleri için x, a'ya yaklaşır. Sol el sınırı ve sağ el sınırı eşit olmadığında, sınır mevcut değildir.

Bir fonksiyonu düşünelim -

f(x) = (x - 3)/|x - 3|

Lim _{x-> 3} f (x) 'in var olmadığını göstereceğiz . MATLAB, bu gerçeği iki şekilde oluşturmamıza yardımcı olur -

Fonksiyonun grafiğini çizerek ve süreksizliği göstererek.
Limitleri hesaplayarak ve her ikisinin de farklı olduğunu göstererek.

Solak ve sağ elini kullanan sınırlar, 'sol' ve 'sağ' karakter dizilerinin son bağımsız değişken olarak sınır komutuna geçirilmesiyle hesaplanır.

Misal

Bir komut dosyası oluşturun ve aşağıdaki kodu içine yazın -

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

Dosyayı çalıştırdığınızda, MATLAB aşağıdaki grafiği çizer

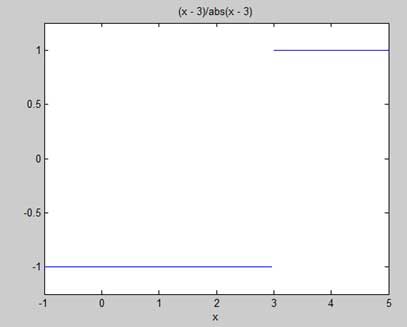
Bundan sonra aşağıdaki çıktı görüntülenir -

l =
   -1
  
r =
   1