MATLAB - Diferansiyel

MATLAB, diffsembolik türevleri hesaplamak için komut. En basit haliyle, ayırt etmek istediğiniz işlevi, diff komutunu bir argüman olarak iletirsiniz.

Örneğin, f (t) = 3t ² + 2t ^-2 fonksiyonunun türevini hesaplayalım.

Misal

Bir komut dosyası oluşturun ve aşağıdaki kodu içine yazın -

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

Yukarıdaki kod derlendiğinde ve yürütüldüğünde, aşağıdaki sonucu verir -

ans =
6*t - 4/t^3

Aşağıda, yukarıdaki hesaplamanın Oktav eşdeğeri -

pkg load symbolic
symbols

t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

Octave, kodu yürütür ve aşağıdaki sonucu döndürür -

ans =
   -(4.0)*t^(-3.0)+(6.0)*t

Temel Farklılaşma Kurallarının Doğrulanması

Fonksiyonların farklılaşması için çeşitli denklemleri veya kuralları kısaca belirtip bu kuralları doğrulayalım. Bu amaçla, birinci dereceden türev için f '(x) ve ikinci dereceden türev için f "(x) yazacağız.

Aşağıdakiler farklılaşma kurallarıdır -

Kural 1

Herhangi bir f ve g fonksiyonu için ve herhangi bir gerçek sayı a ve b, fonksiyonun türevidir -

h(x) = af(x) + bg(x) x'e göre verilir -

h'(x) = af'(x) + bg'(x)

Kural 2

sum ve subtraction kurallar f ve g iki fonksiyonsa, f 've g'nin sırasıyla türevleri olduğunu belirtir, o zaman,

(f + g)' = f' + g'

(f - g)' = f' - g'

Kural 3

product kural, f ve g iki fonksiyonsa, f 've g'nin sırasıyla türevleri olduğunu belirtir, o zaman,

(f.g)' = f'.g + g'.f

Kural 4

quotient kural, f ve g iki fonksiyonsa, f 've g'nin sırasıyla türevleri olduğunu belirtir, o zaman,

(f/g)' = (f'.g - g'.f)/g²

Kural 5

polynomial veya temel güç kuralı, eğer y = f(x) = xⁿ, sonra f' = n. x^(n-1)

Bu kuralın doğrudan bir sonucu, herhangi bir sabitin türevinin sıfır olmasıdır, yani y = k, herhangi bir sabit, o zaman

f' = 0

Kural 6

chain kural, bir fonksiyonun fonksiyonunun türevinin h(x) = f(g(x)) x'e göre,

h'(x)= f'(g(x)).g'(x)

Misal

Bir komut dosyası oluşturun ve aşağıdaki kodu içine yazın -

syms x
syms t

f = (x + 2)*(x^2 + 3)
der1 = diff(f)

f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)

f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)

f = (x^2 + 1)^17
der5 = diff(f)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

Dosyayı çalıştırdığınızda, MATLAB aşağıdaki sonucu görüntüler -

f =
   (x^2 + 3)*(x + 2)
 
   der1 =
   2*x*(x + 2) + x^2 + 3
  
f =
   (t^(1/2) + t^3)*(t^2 + 3)
 
   der2 =
   (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
  
f =
   (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
  
der3 =
   (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
 
f =
   (2*x^2 + 3*x)/(x^3 + 1)
  
der4 =
   (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
  
f =
   (x^2 + 1)^17
  
der5 =
   34*x*(x^2 + 1)^16
  
f =
   1/(t^3 + 3*t^2 + 5*t - 9)^6
  
der6 =
   -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

Aşağıda, yukarıdaki hesaplamanın Oktav eşdeğeri -

pkg load symbolic
symbols

x = sym("x");
t = sym("t");

f = (x + 2)*(x^2 + 3) 
der1 = differentiate(f,x) 

f = (t^2 + 3)*(t^(1/2) + t^3) 
der2 = differentiate(f,t) 

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) 
der3 = differentiate(f,x) 

f = (2*x^2 + 3*x)/(x^3 + 1) 
der4 = differentiate(f,x) 

f = (x^2 + 1)^17 
der5 = differentiate(f,x) 

f = (t^3 + 3* t^2 + 5*t -9)^(-6) 
der6 = differentiate(f,t)

Octave, kodu yürütür ve aşağıdaki sonucu döndürür -

f =

(2.0+x)*(3.0+x^(2.0))
der1 =

3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =

(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =

(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =

(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =

(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =

(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =

(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =

(1.0+x^(2.0))^(17.0)
der5 =

(34.0)*(1.0+x^(2.0))^(16.0)*x
f =

(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =

-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)

Üstel, Logaritmik ve Trigonometrik Fonksiyonların Türevleri

Aşağıdaki tablo, yaygın olarak kullanılan üstel, logaritmik ve trigonometrik fonksiyonların türevlerini göstermektedir -

Fonksiyon	Türev
c^a.x	c ^a.x .ln ca (ln doğal logaritmadır)
e^x	e ^x
ln x	1 / x
ln_cx	1 / x.ln c
x^x	x ^x . (1 + ln x)
sin(x)	çünkü (x)
cos(x)	-sin (x)
tan(x)	saniye ² (x) veya 1 / cos ² (x) veya 1 + tan ² (x)
cot(x)	-csc ² (x) veya -1 / sin ² (x) veya - (1 + cot ² (x))
sec(x)	saniye (x) .tan (x)
csc(x)	-csc (x) .cot (x)

Misal

Bir komut dosyası oluşturun ve aşağıdaki kodu içine yazın -

syms x
y = exp(x)
diff(y)

y = x^9
diff(y)

y = sin(x)
diff(y)

y = tan(x)
diff(y)

y = cos(x)
diff(y)

y = log(x)
diff(y)

y = log10(x)
diff(y)

y = sin(x)^2
diff(y)

y = cos(3*x^2 + 2*x + 1)
diff(y)

y = exp(x)/sin(x)
diff(y)

Dosyayı çalıştırdığınızda, MATLAB aşağıdaki sonucu görüntüler -

y =
   exp(x)
   ans =
   exp(x)

y =
   x^9
   ans =
   9*x^8
  
y =
   sin(x)
   ans =
   cos(x)
  
y =
   tan(x)
   ans =
   tan(x)^2 + 1
 
y =
   cos(x)
   ans =
   -sin(x)
  
y =
   log(x)
   ans =
   1/x
  
y =
   log(x)/log(10)
   ans =
   1/(x*log(10))
 
y =
   sin(x)^2
   ans =
   2*cos(x)*sin(x)
 
y =
   cos(3*x^2 + 2*x + 1)
   ans =
   -sin(3*x^2 + 2*x + 1)*(6*x + 2)
  
y =
   exp(x)/sin(x)
   ans =
   exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

Aşağıda, yukarıdaki hesaplamanın Oktav eşdeğeri -

pkg load symbolic
symbols

x = sym("x");
y = Exp(x)
differentiate(y,x)

y = x^9
differentiate(y,x)

y = Sin(x)
differentiate(y,x)

y = Tan(x)
differentiate(y,x)

y = Cos(x)
differentiate(y,x)

y = Log(x)
differentiate(y,x)

% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)

y = Sin(x)^2
differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)

y = Exp(x)/Sin(x)
differentiate(y,x)

Octave, kodu yürütür ve aşağıdaki sonucu döndürür -

y =

exp(x)
ans =

exp(x)
y =

x^(9.0)
ans =

(9.0)*x^(8.0)
y =

sin(x)
ans =

cos(x)
y =

tan(x)
ans =

1+tan(x)^2
y =

cos(x)
ans =

-sin(x)
y =

log(x)
ans =

x^(-1)
y =

sin(x)^(2.0)
ans =

(2.0)*sin(x)*cos(x)
y =

cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =

-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =

sin(x)^(-1)*exp(x)
ans =

sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)

Yüksek Dereceli Türevlerin Hesaplanması

Bir f fonksiyonunun daha yüksek türevlerini hesaplamak için sözdizimini kullanıyoruz diff(f,n).

Y = f (x) = x .e ^-3x fonksiyonunun ikinci türevini hesaplayalım

f = x*exp(-3*x);
diff(f, 2)

MATLAB kodu yürütür ve aşağıdaki sonucu döndürür -

ans =
9*x*exp(-3*x) - 6*exp(-3*x)

Aşağıda, yukarıdaki hesaplamanın Oktav eşdeğeri -

pkg load symbolic
symbols

x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)

Octave, kodu yürütür ve aşağıdaki sonucu döndürür -

ans =

(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)

Misal

Bu örnekte bir sorunu çözelim. Bir işlev göz önüne alındığınday = f(x) = 3 sin(x) + 7 cos(5x). Denklemin olup olmadığını bulmamız gerekecekf" + f = -5cos(2x) doğrudur.

Bir komut dosyası oluşturun ve aşağıdaki kodu içine yazın -

syms x
y = 3*sin(x)+7*cos(5*x);  % defining the function
lhs = diff(y,2)+y;        %evaluting the lhs of the equation
rhs = -5*cos(2*x);        %rhs of the equation
if(isequal(lhs,rhs))
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Dosyayı çalıştırdığınızda, aşağıdaki sonucu görüntüler -

No, the equation does not hold true
Value of LHS is: 
-168*cos(5*x)

Aşağıda, yukarıdaki hesaplamanın Oktav eşdeğeri -

pkg load symbolic
symbols

x = sym("x");
y = 3*Sin(x)+7*Cos(5*x);           % defining the function
lhs = differentiate(y, x, 2) + y;  %evaluting the lhs of the equation
rhs = -5*Cos(2*x);                 %rhs of the equation

if(lhs == rhs)
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Octave, kodu yürütür ve aşağıdaki sonucu döndürür -

No, the equation does not hold true
Value of LHS is: 
-(168.0)*cos((5.0)*x)

Bir Eğrinin Maksimum ve Minimumlarını Bulmak

Bir grafik için yerel maksimumları ve minimumları arıyorsak, temel olarak belirli bir konumdaki fonksiyonun grafiğindeki en yüksek veya en düşük noktaları veya sembolik değişkenin belirli bir değer aralığını arıyoruz.

Y = f (x) fonksiyonu için, grafiğin sıfır eğime sahip olduğu noktalar stationary points. Başka bir deyişle, sabit noktalar f '(x) = 0'dır.

Farklılaştırdığımız bir fonksiyonun durağan noktalarını bulmak için türevi sıfıra eşitlememiz ve denklemi çözmemiz gerekir.

Misal

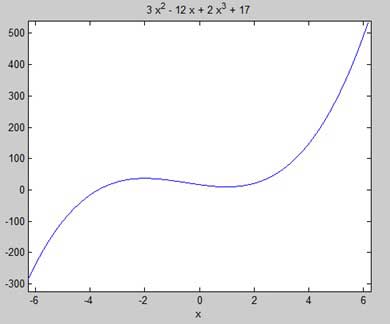
F (x) = 2x ³ + 3x ² - 12x + 17 fonksiyonunun durağan noktalarını bulalım

Aşağıdaki adımları uygulayın -

First let us enter the function and plot its graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y)

MATLAB kodu çalıştırır ve aşağıdaki grafiği döndürür -

İşte yukarıdaki örnek için Octave eşdeğer kodu -

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)
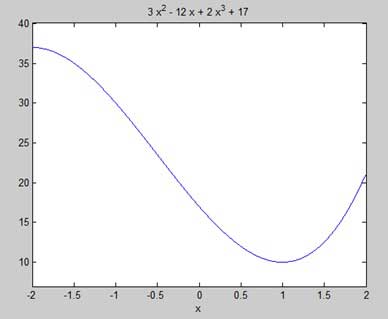
print -deps graph.eps

Our aim is to find some local maxima and minima on the graph, so let us find the local maxima and minima for the interval [-2, 2] on the graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y, [-2, 2])

MATLAB kodu çalıştırır ve aşağıdaki grafiği döndürür -

İşte yukarıdaki örnek için Octave eşdeğer kodu -

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])
print -deps graph.eps

Next, let us compute the derivative.

g = diff(y)

MATLAB kodu yürütür ve aşağıdaki sonucu döndürür -

g =
   6*x^2 + 6*x - 12

İşte yukarıdaki hesaplamanın Oktav eşdeğeri -

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

Octave, kodu yürütür ve aşağıdaki sonucu döndürür -

g =
   -12.0+(6.0)*x+(6.0)*x^(2.0)

Let us solve the derivative function, g, to get the values where it becomes zero.

s = solve(g)

MATLAB kodu yürütür ve aşağıdaki sonucu döndürür -

s =
   1
   -2

Aşağıda, yukarıdaki hesaplamanın Oktav eşdeğeri -

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])

Octave, kodu yürütür ve aşağıdaki sonucu döndürür -

g =

-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =

  -2
   1

This agrees with our plot. So let us evaluate the function f at the critical points x = 1, -2. Sembolik bir fonksiyondaki bir değeri, subs komut.

subs(y, 1), subs(y, -2)

MATLAB kodu yürütür ve aşağıdaki sonucu döndürür -

ans =
   10
ans =
   37

Aşağıda, yukarıdaki hesaplamanın Oktav eşdeğeri -

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)

ans =
   10.0
ans =
   37.0-4.6734207789940138748E-18*I

Bu nedenle, f (x) = 2x ³ + 3x ² - 12x + 17 fonksiyonunun [-2,2] aralığında minimum ve maksimum değerleri 10 ve 37'dir.

Diferansiyel Denklemleri Çözme

MATLAB, dsolve diferansiyel denklemleri sembolik olarak çözmek için komut.

En temel formu dsolve tek bir denklemin çözümünü bulma komutu

dsolve('eqn')

nerede eqn denklemi girmek için kullanılan bir metin dizesidir.

MATLAB'ın C1, C2 vb. Olarak etiketlediği bir dizi rastgele sabitle sembolik bir çözüm döndürür.

Aşağıdaki denklemi takip eden virgülle ayrılmış liste olarak, problem için başlangıç ve sınır koşullarını da belirtebilirsiniz:

dsolve('eqn','cond1', 'cond2',…)

Dsolve komutunun kullanılması amacıyla, derivatives are indicated with a D. Örneğin, f '(t) = -2 * f + maliyet (t) gibi bir denklem - olarak girilir

'Df = -2*f + cos(t)'

Daha yüksek türevler, türevin sırasına göre D'yi takip ederek gösterilir.

Örneğin f "(x) + 2f '(x) = 5sin3x denklemi - olarak girilmelidir

'D2y + 2Dy = 5*sin(3*x)'

Birinci derece diferansiyel denklemin basit bir örneğini ele alalım: y '= 5y.

s = dsolve('Dy = 5*y')

MATLAB kodu yürütür ve aşağıdaki sonucu döndürür -

s =
   C2*exp(5*t)

İkinci dereceden diferansiyel denklemin başka bir örneğini ele alalım: y "- y = 0, y (0) = -1, y '(0) = 2.

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

MATLAB kodu yürütür ve aşağıdaki sonucu döndürür -

ans =
   exp(t)/2 - (3*exp(-t))/2