Hesaplamalı Grafikler
Geri yayılım, hesaplamalı grafikler kullanılarak Tensorflow, Torch, Theano vb. Gibi derin öğrenme çerçevelerinde uygulanır. Daha da önemlisi, hesaplama grafiklerinde geri yayılmayı anlamak, birkaç farklı algoritmayı ve zaman içinde geri dönüş ve geri dönüş gibi varyasyonlarını paylaşılan ağırlıklarla birleştirir. Her şey bir hesaplama grafiğine dönüştürüldüğünde, bunlar hala aynı algoritmadır - sadece hesaplama grafiklerinde geriye doğru yayılma.
Hesaplamalı Grafik nedir
Hesaplamalı grafik, düğümlerin matematiksel işlemlere karşılık geldiği yönlendirilmiş bir grafik olarak tanımlanır. Hesaplamalı grafikler, matematiksel bir ifadeyi ifade etmenin ve değerlendirmenin bir yoludur.
Örneğin, işte basit bir matematiksel denklem -
$$ p = x + y $$
Yukarıdaki denklemin hesaplama grafiğini aşağıdaki gibi çizebiliriz.
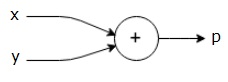
Yukarıdaki hesaplama grafiğinde, iki giriş değişkeni x ve y ve bir çıkış q olan bir toplama düğümü ("+" işaretli düğüm) vardır.
Biraz daha karmaşık başka bir örnek alalım. Aşağıdaki denkleme sahibiz.
$$ g = \ left (x + y \ right) \ ast z $$
Yukarıdaki denklem aşağıdaki hesaplama grafiğiyle temsil edilmektedir.
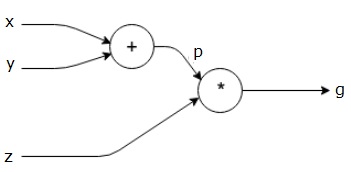
Hesaplamalı Grafikler ve Geri Yayımlama
Hesaplamalı grafikler ve geri yayılım, her ikisi de sinir ağlarını eğitmek için derin öğrenmede önemli temel kavramlardır.
Doğrudan geçiş
İleri geçiş, hesaplamalı grafiklerle temsil edilen matematiksel ifadenin değerini değerlendirme prosedürüdür. İleri geçiş yapmak, değeri değişkenlerden ileriye doğru soldan (giriş) çıkışın olduğu sağa doğru geçirdiğimiz anlamına gelir.
Tüm girdilere bir değer vererek bir örnek ele alalım. Aşağıdaki değerlerin tüm girişlere verildiğini varsayalım.
$$ x = 1, y = 3, z = −3 $$
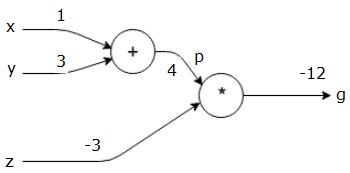
Bu değerleri girişlere vererek ileri geçiş gerçekleştirebilir ve her bir düğüm üzerindeki çıkışlar için aşağıdaki değerleri alabiliriz.
İlk olarak, p = 4 elde etmek için x = 1 ve y = 3 değerlerini kullanıyoruz.

Daha sonra g = -12 elde etmek için p = 4 ve z = -3'ü kullanırız. Soldan sağa doğru ilerliyoruz.
Geriye Pasın Hedefleri
Geriye doğru geçişte amacımız, her girdi için gradyanları nihai çıktıya göre hesaplamaktır. Bu gradyanlar, gradyan inişini kullanarak sinir ağını eğitmek için gereklidir.
Örneğin, aşağıdaki gradyanları istiyoruz.
İstenilen gradyanlar
$$ \ frac {\ bölümlü x} {\ bölümlü f}, \ frac {\ bölüm y} {\ bölümlü f}, \ frac {\ bölüm z} {\ bölümlü f} $$
Geri geçiş (geri yayılım)
Geri geçişe, nihai çıktının (kendisi!) Nihai çıktıya göre türevini bularak başlıyoruz. Böylece, özdeşliğin türetilmesi ile sonuçlanacaktır ve değer bire eşittir.
$$ \ frac {\ kısmi g} {\ kısmi g} = 1 $$
Hesaplama grafiğimiz artık aşağıda gösterildiği gibi görünüyor -
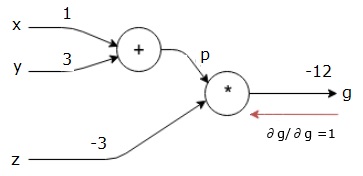
Daha sonra geriye doğru geçişi "*" işleminden yapacağız. Degradeleri p ve z'de hesaplayacağız. G = p * z olduğundan, bunu biliyoruz -
$$ \ frac {\ kısmi g} {\ kısmi z} = p $$
$$ \ frac {\ kısmi g} {\ kısmi p} = z $$
Z ve p'nin değerlerini ileri geçişten zaten biliyoruz. Bu nedenle, biz -
$$ \ frac {\ kısmi g} {\ kısmi z} = p = 4 $$
ve
$$ \ frac {\ kısmi g} {\ kısmi p} = z = -3 $$
X ve y'deki gradyanları hesaplamak istiyoruz -
$$ \ frac {\ kısmi g} {\ kısmi x}, \ frac {\ kısmi g} {\ kısmi y} $$
Ancak, bunu verimli bir şekilde yapmak istiyoruz (x ve g bu grafikte yalnızca iki atlama uzaklıkta olmasına rağmen, birbirlerinden gerçekten uzak olduklarını hayal edin). Bu değerleri verimli bir şekilde hesaplamak için, farklılaşma zincir kuralını kullanacağız. Zincir kuralına göre, biz -
$$ \ frac {\ kısmi g} {\ kısmi x} = \ frac {\ kısmi g} {\ kısmi p} \ ast \ frac {\ kısmi p} {\ kısmi x} $$
$$ \ frac {\ kısmi g} {\ kısmi y} = \ frac {\ kısmi g} {\ kısmi p} \ ast \ frac {\ kısmi p} {\ kısmi y} $$
Ancak dg / dp = -3, dp / dx ve dp / dy'nin kolay olduğunu zaten biliyoruz çünkü p doğrudan x ve y'ye bağlıdır. Biz -
$$ p = x + y \ Rightarrow \ frac {\ partial x} {\ partly p} = 1, \ frac {\ partial y} {\ partly p} = 1 $$
Bu nedenle, biz -
$$ \ frac {\ kısmi g} {\ kısmi f} = \ frac {\ kısmi g} {\ kısmi p} \ ast \ frac {\ kısmi p} {\ kısmi x} = \ sol (-3 \ sağ) .1 = -3 $$
Ek olarak, y girişi için -
$$ \ frac {\ kısmi g} {\ kısmi y} = \ frac {\ kısmi g} {\ kısmi p} \ ast \ frac {\ kısmi p} {\ kısmi y} = \ left (-3 \ sağ) .1 = -3 $$
Bunu geriye doğru yapmamızın ana nedeni, x'teki gradyanı hesaplamamız gerektiğinde, yalnızca önceden hesaplanmış değerleri ve dq / dx'i (aynı düğümün girdisine göre düğüm çıktısının türevi) kullanmamızdır. Küresel bir değeri hesaplamak için yerel bilgileri kullandık.
Bir sinir ağını eğitmek için adımlar
Bir sinir ağını eğitmek için şu adımları izleyin -
Veri kümesindeki x veri noktası için, girdi olarak x ile ileri doğru geçiyoruz ve çıktı olarak c maliyetini hesaplıyoruz.
C'den başlayarak geriye doğru geçiş yapıyoruz ve grafikteki tüm düğümler için gradyanları hesaplıyoruz. Bu, sinir ağı ağırlıklarını temsil eden düğümleri içerir.
Daha sonra ağırlıkları W = W - öğrenme oranı * gradyanları yaparak güncelliyoruz.
Durdurma kriterleri karşılanana kadar bu işlemi tekrar ederiz.