PyTorch - Hızlı Kılavuz

PyTorch, Python için açık kaynaklı bir makine öğrenimi kitaplığı olarak tanımlanır. Doğal dil işleme gibi uygulamalar için kullanılır. Başlangıçta Facebook yapay zeka araştırma grubu ve üzerine inşa edilen olasılıklı programlama için Uber'in Pyro yazılımı tarafından geliştirilmiştir.

Başlangıçta PyTorch, Hugh Perkins tarafından Torch çerçevesine dayalı LusJIT için bir Python sarıcı olarak geliştirildi. İki PyTorch çeşidi vardır.

PyTorch, arka uç kodu için aynı çekirdek C kitaplıklarını paylaşırken Torch'u Python'da yeniden tasarlar ve uygular. PyTorch geliştiricileri, Python'u verimli bir şekilde çalıştırmak için bu arka uç kodunu ayarladı. Ayrıca, Lua tabanlı Torch'u yapan genişletilebilirlik özelliklerinin yanı sıra GPU tabanlı donanım hızlandırmayı da korudular.

Özellikleri

PyTorch'un temel özellikleri aşağıda belirtilmiştir -

Easy Interface- PyTorch, kullanımı kolay API sunar; dolayısıyla Python üzerinde çalıştırılması ve çalıştırılması çok basit kabul edilir. Bu çerçevede kod yürütme oldukça kolaydır.

Python usage- Bu kütüphane, Python veri bilimi yığınıyla sorunsuz bir şekilde bütünleşen Pythonic olarak kabul edilir. Böylece, Python ortamının sunduğu tüm hizmetlerden ve işlevlerden yararlanabilir.

Computational graphs- PyTorch, dinamik hesaplama grafikleri sunan mükemmel bir platform sağlar. Böylelikle bir kullanıcı çalışma sırasında bunları değiştirebilir. Bu, bir geliştiricinin bir sinir ağı modeli oluşturmak için ne kadar bellek gerektiğine dair hiçbir fikri olmadığında oldukça kullanışlıdır.

PyTorch, aşağıda verildiği gibi üç seviyeli soyutlamaya sahip olduğu bilinmektedir -

• Tensor - GPU üzerinde çalışan zorunlu n boyutlu dizi.

• Değişken - Hesaplamalı grafikte düğüm. Bu, verileri ve gradyanı depolar.

• Modül - Durum veya öğrenilebilir ağırlıkları depolayacak sinir ağı katmanı.

PyTorch'un Avantajları

Aşağıdakiler PyTorch'un avantajlarıdır -

• Kodda hata ayıklamak ve anlamak kolaydır.

• Torch olarak birçok katman içerir.

• Çok sayıda kayıp işlevi içerir.

• GPU'lara NumPy uzantısı olarak düşünülebilir.

• Yapısı hesaplamanın kendisine bağlı olan ağların kurulmasına izin verir.

TensorFlow ve PyTorch

Aşağıda TensorFlow ve PyTorch arasındaki temel farkları inceleyeceğiz -

PyTorch	TensorFlow
PyTorch, Facebook'ta aktif olarak kullanılan lua tabanlı Torch çerçevesi ile yakından ilgilidir.	TensorFlow, Google Brain tarafından geliştirilmiştir ve Google'da aktif olarak kullanılmaktadır.
PyTorch, diğer rakip teknolojilere kıyasla nispeten yenidir.	TensorFlow yeni değildir ve birçok araştırmacı ve sektör profesyoneli tarafından gidilecek bir araç olarak kabul edilmektedir.
PyTorch her şeyi zorunlu ve dinamik bir şekilde içerir.	TensorFlow, statik ve dinamik grafikleri bir kombinasyon olarak içerir.
PyTorch'ta hesaplama grafiği çalışma süresi sırasında tanımlanır.	TensorFlow herhangi bir çalışma süresi seçeneği içermez.
PyTorch, mobil ve gömülü çerçeveler için özellikli dağıtım içerir.	TensorFlow, gömülü çerçeveler için daha iyi çalışır.

PyTorch, popüler bir derin öğrenme çerçevesidir. Bu eğiticide, işletim sistemimiz olarak "Windows 10" u ele alıyoruz. Başarılı bir çevresel kurulum için adımlar aşağıdaki gibidir -

Aşama 1

Aşağıdaki bağlantı, PyTorch için uygun paketleri içeren bir paket listesi içerir.

https://drive.google.com/drive/folders/0B-X0-FlSGfCYdTNldW02UGl4MXM

Tek yapmanız gereken, ilgili paketleri indirmek ve aşağıdaki ekran görüntülerinde gösterildiği gibi kurmaktır -

Adım 2

Anaconda Framework kullanılarak PyTorch çerçevesinin kurulumunun doğrulanmasını içerir.

Aynı şeyi doğrulamak için aşağıdaki komut kullanılır -

conda list

"Conda listesi" kurulu olan çerçevelerin listesini gösterir.

Vurgulanan kısım, PyTorch'un sistemimize başarıyla kurulduğunu gösterir.

Matematik, herhangi bir makine öğrenimi algoritmasında hayati önem taşır ve belirli bir şekilde tasarlanmış doğru algoritmayı elde etmek için matematiğin çeşitli temel kavramlarını içerir.

Makine öğrenimi ve veri bilimi için matematik konularının önemi aşağıda belirtilmiştir -

Şimdi, Doğal Dil İşleme açısından önemli olan makine öğreniminin temel matematiksel kavramlarına odaklanalım -

Vektörler

Vektör, sürekli veya kesikli sayılar dizisi olarak kabul edilir ve vektörlerden oluşan uzaya vektör uzayı denir. Vektörlerin uzay boyutları sonlu veya sonsuz olabilir, ancak makine öğrenimi ve veri bilimi problemlerinin sabit uzunluklu vektörlerle ilgilendiği gözlemlenmiştir.

Vektör gösterimi aşağıda belirtildiği gibi görüntülenir -

temp = torch.FloatTensor([23,24,24.5,26,27.2,23.0])
temp.size()
Output - torch.Size([6])

Makine öğreniminde çok boyutlu verilerle ilgileniyoruz. Dolayısıyla vektörler çok önemli hale gelir ve herhangi bir tahmin problem ifadesi için girdi özellikleri olarak kabul edilir.

Skaler

Skalarlar, yalnızca bir değer içeren sıfır boyutlara sahip olarak adlandırılır. PyTorch söz konusu olduğunda, sıfır boyutlu özel bir tensör içermez; dolayısıyla beyan aşağıdaki şekilde yapılacaktır -

x = torch.rand(10)
x.size()
Output - torch.Size([10])

Matrisler

Yapılandırılmış verilerin çoğu genellikle tablolar veya belirli bir matris şeklinde temsil edilir. Python scikit-learn makine öğrenimi kitaplığında kolayca bulunabilen Boston House Fiyatları adlı bir veri kümesi kullanacağız.

boston_tensor = torch.from_numpy(boston.data)
boston_tensor.size()
Output: torch.Size([506, 13])
boston_tensor[:2]
Output:
Columns 0 to 7
0.0063 18.0000 2.3100 0.0000 0.5380 6.5750 65.2000 4.0900
0.0273 0.0000 7.0700 0.0000 0.4690 6.4210 78.9000 4.9671
Columns 8 to 12
1.0000 296.0000 15.3000 396.9000 4.9800
2.0000 242.0000 17.8000 396.9000 9.1400

Sinir ağının ana prensibi, yapay nöron veya algılayıcı gibi temel unsurların bir koleksiyonunu içerir. Toplam aktivasyon potansiyelinden büyükse bir ikili çıktı üreten x1, x2… .. xn gibi birkaç temel giriş içerir.

Örnek nöronun şematik temsili aşağıda belirtilmiştir -

Üretilen çıktı, aktivasyon potansiyeli veya önyargı ile ağırlıklı toplam olarak kabul edilebilir.

$$Output=\sum_jw_jx_j+Bias$$

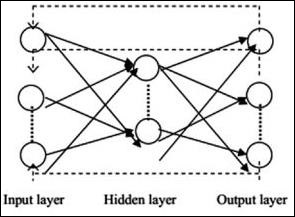
Tipik sinir ağı mimarisi aşağıda açıklanmıştır -

Giriş ve çıkış arasındaki katmanlara gizli katmanlar adı verilir ve katmanlar arasındaki bağlantıların yoğunluğu ve türü konfigürasyondur. Örneğin, tamamen bağlı bir konfigürasyon, L + 1'inkilere bağlı L katmanının tüm nöronlarına sahiptir. Daha belirgin bir yerelleştirme için, yalnızca yerel bir mahalleyi, örneğin dokuz nöronu bir sonraki katmana bağlayabiliriz. Şekil 1-9, yoğun bağlantılara sahip iki gizli katmanı göstermektedir.

Çeşitli sinir ağları aşağıdaki gibidir -

İleri Beslemeli Sinir Ağları

İleri beslemeli sinir ağları, sinir ağı ailesinin temel birimlerini içerir. Bu tür bir sinir ağındaki verilerin hareketi, mevcut gizli katmanlar aracılığıyla girdi katmanından çıktı katmanına doğrudur. Bir katmanın çıktısı, ağ mimarisindeki her türlü döngü üzerinde kısıtlamalara sahip giriş katmanı olarak hizmet eder.

Tekrarlayan Sinir Ağları

Tekrarlayan Sinir Ağları, veri modelinin bir süre boyunca sonuç olarak değiştiği zamandır. RNN'de, belirtilen sinir ağında girdi parametrelerini kabul etmek ve çıktı parametrelerini görüntülemek için aynı katman uygulanır.

Sinir ağları torch.nn paketi kullanılarak oluşturulabilir.

Basit bir ileri beslemeli ağdır. Girdiyi alır, birkaç katmandan arka arkaya besler ve sonunda çıktıyı verir.

PyTorch'un yardımıyla, bir sinir ağı için tipik eğitim prosedürü için aşağıdaki adımları kullanabiliriz -

• Bazı öğrenilebilir parametreleri (veya ağırlıkları) olan sinir ağını tanımlayın.
• Veri girdilerinin üzerinde yineleyin.
• Ağ üzerinden işlem girişi.
• Kaybı hesaplayın (çıktının doğru olmaktan ne kadar uzak olduğu).
• Gradyanları ağın parametrelerine geri yayın.
• Genellikle aşağıda verilen basit bir güncelleme kullanarak ağın ağırlıklarını güncelleyin

rule: weight = weight -learning_rate * gradient

Yapay Zeka, günümüzde büyük ölçüde trend oluyor. Makine öğrenimi ve derin öğrenme, yapay zekayı oluşturur. Aşağıda bahsedilen Venn şeması, makine öğrenimi ile derin öğrenmenin ilişkisini açıklamaktadır.

Makine öğrenme

Makine öğrenimi, bilgisayarların tasarlanan ve programlanan algoritmalara göre hareket etmesini sağlayan bilim sanatıdır. Pek çok araştırmacı, makine öğreniminin insan seviyesinde yapay zekaya doğru ilerleme kaydetmenin en iyi yolu olduğunu düşünüyor. Gibi çeşitli desen türlerini içerir -

• Denetimli Öğrenme Modeli
• Denetimsiz Öğrenme Modeli

Derin Öğrenme

Derin öğrenme, ilgili algoritmaların Yapay Sinir Ağları adı verilen beynin yapısı ve işlevinden ilham aldığı bir makine öğrenimi alt alanıdır.

Derin öğrenme, denetimli öğrenme veya etiketli veri ve algoritmalardan öğrenme yoluyla büyük önem kazanmıştır. Derin öğrenmedeki her algoritma aynı süreçten geçer. Girdinin doğrusal olmayan dönüşüm hiyerarşisini içerir ve çıktı olarak istatistiksel bir model oluşturmak için kullanır.

Makine öğrenimi süreci aşağıdaki adımlar kullanılarak tanımlanır -

• İlgili veri setlerini belirler ve analize hazırlar.
• Kullanılacak algoritma türünü seçer.
• Kullanılan algoritmaya göre analitik bir model oluşturur.
• Modeli test veri kümeleri üzerinde eğitir ve gerektiğinde revize eder.
• Modeli test puanları oluşturmak için çalıştırır.

Bu bölümde, Makine ve Derin öğrenme kavramları arasındaki temel farkı tartışacağız.

Data miktarı

Makine öğrenimi, farklı miktarlarda verilerle çalışır ve esas olarak küçük miktarlarda veri için kullanılır. Öte yandan derin öğrenme, veri miktarı hızla artarsa ​​verimli bir şekilde çalışır. Aşağıdaki diyagram, veri miktarına göre makine öğreniminin ve derin öğrenmenin çalışmasını göstermektedir -

Donanım Bağımlılıkları

Derin öğrenme algoritmaları, geleneksel makine öğrenimi algoritmalarının aksine büyük ölçüde ileri teknoloji makinelere bağlı olacak şekilde tasarlanmıştır. Derin öğrenme algoritmaları, büyük bir donanım desteği gerektiren büyük miktarda matris çarpma işlemi gerçekleştirir.

Özellik Mühendisliği

Özellik mühendisliği, verilerin karmaşıklığını azaltmak ve öğrenme algoritmaları tarafından görülebilen desenler oluşturmak için alan bilgisini belirtilen özelliklere yerleştirme sürecidir.

Örneğin, geleneksel makine öğrenimi kalıpları, özellik mühendisliği süreci için gereken piksellere ve diğer özelliklere odaklanır. Derin öğrenme algoritmaları, verilerdeki üst düzey özelliklere odaklanır. Her yeni sorun için yeni özellik çıkarıcı geliştirme görevini azaltır.

PyTorch, sinir ağları oluşturma ve uygulama özelliğine sahiptir. Bu bölümde, tek bir çıktı birimi geliştiren tek bir gizli katman ile basit bir sinir ağı oluşturacağız.

PyTorch kullanarak ilk sinir ağını uygulamak için aşağıdaki adımları kullanacağız -

Aşama 1

Öncelikle, aşağıdaki komutu kullanarak PyTorch kitaplığını içe aktarmamız gerekir -

import torch 
import torch.nn as nn

Adım 2

Sinir ağını yürütmeye başlamak için tüm katmanları ve toplu iş boyutunu aşağıda gösterildiği gibi tanımlayın -

# Defining input size, hidden layer size, output size and batch size respectively
n_in, n_h, n_out, batch_size = 10, 5, 1, 10

Aşama 3

Sinir ağı, ilgili çıktı verilerini almak için bir girdi verisi kombinasyonu içerdiğinden, aşağıda verilen prosedürün aynısını izleyeceğiz -

# Create dummy input and target tensors (data)
x = torch.randn(batch_size, n_in)
y = torch.tensor([[1.0], [0.0], [0.0], 
[1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]])

4. adım

Yerleşik işlevlerin yardımıyla sıralı bir model oluşturun. Aşağıdaki kod satırlarını kullanarak sıralı bir model oluşturun -

# Create a model
model = nn.Sequential(nn.Linear(n_in, n_h),
   nn.ReLU(),
   nn.Linear(n_h, n_out),
   nn.Sigmoid())

Adım 5

Gradient Descent optimizer yardımıyla kayıp fonksiyonunu aşağıda gösterildiği gibi oluşturun -

Construct the loss function
criterion = torch.nn.MSELoss()
# Construct the optimizer (Stochastic Gradient Descent in this case)
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)

6. Adım

Gradyan iniş modelini verilen kod satırlarıyla yineleme döngüsüyle uygulayın -

# Gradient Descent
for epoch in range(50):
   # Forward pass: Compute predicted y by passing x to the model
   y_pred = model(x)

   # Compute and print loss
   loss = criterion(y_pred, y)
   print('epoch: ', epoch,' loss: ', loss.item())

   # Zero gradients, perform a backward pass, and update the weights.
   optimizer.zero_grad()

   # perform a backward pass (backpropagation)
   loss.backward()

   # Update the parameters
   optimizer.step()

7. Adım

Üretilen çıktı aşağıdaki gibidir -

epoch: 0 loss: 0.2545787990093231
epoch: 1 loss: 0.2545052170753479
epoch: 2 loss: 0.254431813955307
epoch: 3 loss: 0.25435858964920044
epoch: 4 loss: 0.2542854845523834
epoch: 5 loss: 0.25421255826950073
epoch: 6 loss: 0.25413978099823
epoch: 7 loss: 0.25406715273857117
epoch: 8 loss: 0.2539947032928467
epoch: 9 loss: 0.25392240285873413
epoch: 10 loss: 0.25385022163391113
epoch: 11 loss: 0.25377824902534485
epoch: 12 loss: 0.2537063956260681
epoch: 13 loss: 0.2536346912384033
epoch: 14 loss: 0.25356316566467285
epoch: 15 loss: 0.25349172949790955
epoch: 16 loss: 0.25342053174972534
epoch: 17 loss: 0.2533493936061859
epoch: 18 loss: 0.2532784342765808
epoch: 19 loss: 0.25320762395858765
epoch: 20 loss: 0.2531369626522064
epoch: 21 loss: 0.25306645035743713
epoch: 22 loss: 0.252996027469635
epoch: 23 loss: 0.2529257833957672
epoch: 24 loss: 0.25285571813583374
epoch: 25 loss: 0.25278574228286743
epoch: 26 loss: 0.25271597504615784
epoch: 27 loss: 0.25264623761177063
epoch: 28 loss: 0.25257670879364014
epoch: 29 loss: 0.2525072991847992
epoch: 30 loss: 0.2524380087852478
epoch: 31 loss: 0.2523689270019531
epoch: 32 loss: 0.25229987502098083
epoch: 33 loss: 0.25223103165626526
epoch: 34 loss: 0.25216227769851685
epoch: 35 loss: 0.252093642950058
epoch: 36 loss: 0.25202515721321106
epoch: 37 loss: 0.2519568204879761
epoch: 38 loss: 0.251888632774353
epoch: 39 loss: 0.25182053446769714
epoch: 40 loss: 0.2517525553703308
epoch: 41 loss: 0.2516847252845764
epoch: 42 loss: 0.2516169846057892
epoch: 43 loss: 0.2515493929386139
epoch: 44 loss: 0.25148195028305054
epoch: 45 loss: 0.25141456723213196
epoch: 46 loss: 0.2513473629951477
epoch: 47 loss: 0.2512802183628082
epoch: 48 loss: 0.2512132525444031
epoch: 49 loss: 0.2511464059352875

Derin öğrenme algoritması eğitimi aşağıdaki adımları içerir -

• Veri hattı oluşturma
• Bir ağ mimarisi oluşturmak
• Bir kayıp işlevi kullanarak mimariyi değerlendirme
• Bir optimizasyon algoritması kullanarak ağ mimarisi ağırlıklarını optimize etme

Belirli bir derin öğrenme algoritmasını eğitmek, bir sinir ağını aşağıda gösterildiği gibi işlevsel bloklara dönüştürmenin tam gerekliliğidir -

Yukarıdaki diyagramla ilgili olarak, herhangi bir derin öğrenme algoritması, giriş verilerinin alınmasını ve bunlara gömülü bir grup katmanı içeren ilgili mimarinin oluşturulmasını içerir.

Yukarıdaki diyagramı gözlemlerseniz, doğruluk, sinir ağının ağırlıklarının optimizasyonu açısından bir kayıp fonksiyonu kullanılarak değerlendirilir.

Bu bölümde, PyTorch'ta en sık kullanılan terimlerden bazılarını tartışacağız.

PyTorch NumPy

Bir PyTorch tensörü, bir NumPy dizisi ile aynıdır. Bir tensör, n boyutlu bir dizidir ve PyTorch'a göre, bu tensörler üzerinde çalışmak için birçok işlev sağlar.

PyTorch tensörleri, sayısal hesaplamalarını hızlandırmak için genellikle GPU'ları kullanır. PyTorch'da oluşturulan bu tensörler, iki katmanlı bir ağı rastgele verilere uydurmak için kullanılabilir. Kullanıcı, ağ üzerinden ileri ve geri geçişleri manuel olarak uygulayabilir.

Değişkenler ve Autograd

Otomatik derecelendirmeyi kullanırken, ağınızın ileri geçişi bir computational graph - Grafikteki düğümler Tensörler olacaktır ve kenarlar, giriş Tensörlerinden çıkış Tensörleri üreten fonksiyonlar olacaktır.

PyTorch Tensörleri, bir değişkenin hesaplama grafiğindeki bir düğümü temsil ettiği değişken nesneler olarak oluşturulabilir.

Dinamik Grafikler

Statik grafikler güzeldir çünkü kullanıcı grafiği önceden optimize edebilir. Programcılar aynı grafiği tekrar tekrar kullanıyorlarsa, bu potansiyel olarak maliyetli ön optimizasyon, aynı grafik tekrar tekrar çalıştırıldığı için sürdürülebilir.

Aralarındaki en büyük fark, Tensor Flow'un hesaplama grafiklerinin statik olması ve PyTorch'un dinamik hesaplama grafikleri kullanmasıdır.

Optim Paketi

PyTorch'daki optim paketi, birçok şekilde uygulanan bir optimizasyon algoritması fikrini özetler ve yaygın olarak kullanılan optimizasyon algoritmalarının örneklerini sunar. Bu, import ifadesi içinde çağrılabilir.

Çoklu işlem

Çoklu işlem aynı işlemleri destekler, böylece tüm tensörler birden fazla işlemci üzerinde çalışır. Kuyruğun verileri paylaşılan belleğe taşınacak ve yalnızca başka bir işleme bir tanıtıcı gönderecektir.

PyTorch, veri setini yüklemek ve hazırlamak için kullanılan torchvision adlı bir paket içerir. Veri kümesinin dönüştürülmesine ve yüklenmesine yardımcı olan Veri Kümesi ve Veri Yükleyicisi olmak üzere iki temel işlevi içerir.

Veri kümesi

Veri kümesi, verilen veri kümesinden bir veri noktasını okumak ve dönüştürmek için kullanılır. Uygulanacak temel sözdizimi aşağıda belirtilmiştir -

trainset = torchvision.datasets.CIFAR10(root = './data', train = True,
   download = True, transform = transform)

DataLoader, verileri karıştırmak ve toplu işlemek için kullanılır. Verileri, çoklu işlem yapan çalışanlarla paralel olarak yüklemek için kullanılabilir.

trainloader = torch.utils.data.DataLoader(trainset, batch_size = 4,
   shuffle = True, num_workers = 2)

Örnek: CSV Dosyasını Yükleme

Csv dosyasını yüklemek için Python paketi Panda'yı kullanıyoruz. Orijinal dosya aşağıdaki formata sahiptir: (görüntü adı, 68 yer işareti - her yer işaretinin eksen, y koordinatları vardır).

landmarks_frame = pd.read_csv('faces/face_landmarks.csv')

n = 65
img_name = landmarks_frame.iloc[n, 0]
landmarks = landmarks_frame.iloc[n, 1:].as_matrix()
landmarks = landmarks.astype('float').reshape(-1, 2)

Bu bölümde, TensorFlow kullanarak doğrusal regresyon uygulamasının temel örneğine odaklanacağız. Lojistik regresyon veya doğrusal regresyon, ayrı ayrı kategorilerin sınıflandırılması için denetlenen bir makine öğrenimi yaklaşımıdır. Bu bölümdeki amacımız, bir kullanıcının tahmin değişkenleri ile bir veya daha fazla bağımsız değişken arasındaki ilişkiyi tahmin edebileceği bir model oluşturmaktır.

Bu iki değişken arasındaki ilişki doğrusal olarak kabul edilir, yani eğer y bağımlı değişkense ve x bağımsız değişken olarak kabul edilirse, iki değişkenin doğrusal regresyon ilişkisi aşağıda belirtilen denklem gibi görünecektir -

Y = Ax+b

Ardından, aşağıda verilen iki önemli kavramı anlamamıza izin veren doğrusal regresyon için bir algoritma tasarlayacağız -

• Maliyet fonksiyonu
• Gradyan İniş Algoritmaları

Doğrusal regresyonun şematik gösterimi aşağıda belirtilmiştir

Sonucu yorumlamak

$$Y=ax+b$$

• Değeri a eğimdir.

• Değeri b ... y − intercept.

• r ... correlation coefficient.

• r² ... correlation coefficient.

Doğrusal regresyon denkleminin grafik görünümü aşağıda belirtilmiştir -

PyTorch kullanarak doğrusal regresyon uygulamak için aşağıdaki adımlar kullanılır -

Aşama 1

Aşağıdaki kodu kullanarak PyTorch'da doğrusal bir regresyon oluşturmak için gerekli paketleri içe aktarın -

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline

sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = True

Adım 2

Aşağıda gösterildiği gibi mevcut veri kümesiyle tek bir eğitim seti oluşturun -

m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)

noise = np.random.randn(256) / 4

y = x * m + c + noise

df = pd.DataFrame()
df['x'] = x
df['y'] = y

sns.lmplot(x ='x', y ='y', data = df)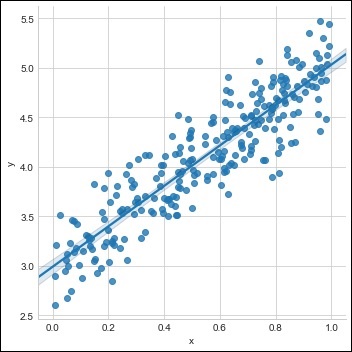

Aşama 3

Aşağıda belirtildiği gibi PyTorch kitaplıkları ile doğrusal regresyon uygulayın -

import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

class LinearRegressionModel(nn.Module):
   def __init__(self, input_dim, output_dim):
      super(LinearRegressionModel, self).__init__()
      self.linear = nn.Linear(input_dim, output_dim)

   def forward(self, x):
      out = self.linear(x)
      return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()

def get_param_values():
   return w.data[0][0], b.data[0]

def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')

Oluşturulan arsa aşağıdaki gibidir -

Derin öğrenme, makine öğreniminin bir bölümüdür ve araştırmacılar tarafından son yıllarda atılan çok önemli bir adım olarak kabul edilmektedir. Derin öğrenme uygulamasının örnekleri, görüntü tanıma ve konuşma tanıma gibi uygulamaları içerir.

İki önemli derin sinir ağı türü aşağıda verilmiştir -

• Evrişimli Sinir Ağları
• Tekrarlayan Sinir Ağları.

Bu bölümde, ilk türe, yani Evrişimli Sinir Ağlarına (CNN) odaklanacağız.

Evrişimli Sinir Ağları

Evrişimli Sinir ağları, verileri birden çok dizi katmanı aracılığıyla işlemek için tasarlanmıştır. Bu tür sinir ağları, görüntü tanıma veya yüz tanıma gibi uygulamalarda kullanılır.

CNN ile diğer herhangi bir sıradan sinir ağı arasındaki temel fark, CNN'nin girdiyi iki boyutlu bir dizi olarak alması ve diğer sinir ağlarının odaklandığı özellik çıkarımına odaklanmak yerine doğrudan görüntüler üzerinde çalışmasıdır.

CNN'in baskın yaklaşımı, tanıma sorunlarının çözümünü içerir. Google ve Facebook gibi önde gelen şirketler, faaliyetlerin daha hızlı yapılmasını sağlamak için tanıma projelerinin araştırma ve geliştirme projelerine yatırım yaptı.

Her evrişimli sinir ağı üç temel fikir içerir -

• Yerel ilgili alanlar
• Convolution
• Pooling

Bu terminolojilerin her birini ayrıntılı olarak anlayalım.

Yerel İlgili Alanlar

CNN, giriş verilerinde bulunan uzamsal korelasyonları kullanır. Sinir ağlarının eşzamanlı katmanlarındaki her biri, bazı giriş nöronlarını birbirine bağlar. Bu belirli bölgeye Yerel Alıcı Alan denir. Yalnızca gizli nöronlara odaklanır. Gizli nöron, belirli sınırın dışındaki değişiklikleri fark etmeden belirtilen alanın içindeki giriş verilerini işleyecektir.

Yerel ilgili alanların oluşturulmasının şema temsili aşağıda belirtilmiştir -

Evrişim

Yukarıdaki şekilde, her bağlantının bir katmandan diğerine hareketle ilişkili bir bağlantıyla birlikte bir gizli nöron ağırlığını öğrendiğini gözlemliyoruz. Burada, bireysel nöronlar zaman zaman bir değişiklik yapar. Bu sürece "evrişim" denir.

Giriş katmanından gizli özellik haritasına bağlantıların eşlenmesi "paylaşılan ağırlıklar" olarak tanımlanır ve dahil edilen önyargı "paylaşılan önyargı" olarak adlandırılır.

Havuzlama

Evrişimli sinir ağları, CNN bildiriminden hemen sonra konumlandırılan havuz katmanlarını kullanır. Kullanıcıdan gelen girdiyi, evrişimli ağlardan çıkan ve yoğunlaştırılmış bir özellik haritası hazırlayan bir özellik haritası olarak alır. Havuz katmanları, önceki katmanların nöronlarıyla katman oluşturmaya yardımcı olur.

PyTorch'un Uygulanması

PyTorch kullanarak Evrişimli Sinir Ağı oluşturmak için aşağıdaki adımlar kullanılır.

Aşama 1

Basit bir sinir ağı oluşturmak için gerekli paketleri içe aktarın.

from torch.autograd import Variable
import torch.nn.functional as F

Adım 2

Evrişimli sinir ağının toplu temsiline sahip bir sınıf oluşturun. X girişi için parti şeklimiz (3, 32, 32) boyutundadır.

class SimpleCNN(torch.nn.Module):
   def __init__(self):
      super(SimpleCNN, self).__init__()
      #Input channels = 3, output channels = 18
      self.conv1 = torch.nn.Conv2d(3, 18, kernel_size = 3, stride = 1, padding = 1)
      self.pool = torch.nn.MaxPool2d(kernel_size = 2, stride = 2, padding = 0)
      #4608 input features, 64 output features (see sizing flow below)
      self.fc1 = torch.nn.Linear(18 * 16 * 16, 64)
      #64 input features, 10 output features for our 10 defined classes
      self.fc2 = torch.nn.Linear(64, 10)

Aşama 3

(3, 32, 32) 'den (18, 32, 32)' ye ilk evrişim boyutunun aktivasyonunu hesaplayın.

Boyutun boyutu (18, 32, 32) yerine (18, 16, 16) olarak değişir. Boyut (18, 16, 16) 'dan (1, 4608)' e değiştiği için sinir ağının giriş katmanının veri boyutunu yeniden şekillendirin.

-1'in bu boyutu verilen diğer boyuttan aldığını hatırlayın.

def forward(self, x):
   x = F.relu(self.conv1(x))
   x = self.pool(x)
   x = x.view(-1, 18 * 16 *16)
   x = F.relu(self.fc1(x))
   #Computes the second fully connected layer (activation applied later)
   #Size changes from (1, 64) to (1, 10)
   x = self.fc2(x)
   return(x)

Tekrarlayan sinir ağları, sıralı bir yaklaşımı izleyen bir tür derin öğrenme odaklı algoritmadır. Sinir ağlarında, her zaman her bir giriş ve çıkışın diğer tüm katmanlardan bağımsız olduğunu varsayıyoruz. Bu tür sinir ağlarına yinelenen adı verilir çünkü matematiksel hesaplamaları birbiri ardına tamamlayarak sıralı bir şekilde gerçekleştirirler.

Aşağıdaki diyagram, tekrarlayan sinir ağlarının tam yaklaşımını ve çalışmasını göstermektedir -

Yukarıdaki şekilde, c1, c2, c3 ve x1, o1'in ilgili çıkışını sağlayan h1, h2 ve h3 gibi bazı gizli giriş değerlerini içeren girişler olarak kabul edilir. Şimdi tekrarlayan sinir ağlarının yardımıyla bir sinüs dalgası oluşturmak için PyTorch'u uygulamaya odaklanacağız.

Eğitim sırasında, modelimize bir seferde bir veri noktası ile bir eğitim yaklaşımı izleyeceğiz. X giriş dizisi 20 veri noktasından oluşur ve hedef sıranın giriş dizisi ile aynı olduğu kabul edilir.

Aşama 1

Aşağıdaki kodu kullanarak tekrarlayan sinir ağlarını uygulamak için gerekli paketleri içe aktarın -

import torch
from torch.autograd import Variable
import numpy as np
import pylab as pl
import torch.nn.init as init

Adım 2

Model hiper parametrelerini, giriş katmanı boyutu 7 olarak ayarlayacağız. Hedef sekansı oluşturmak için 6 bağlam nöronu ve 1 giriş nöronu olacak.

dtype = torch.FloatTensor
input_size, hidden_size, output_size = 7, 6, 1
epochs = 300
seq_length = 20
lr = 0.1
data_time_steps = np.linspace(2, 10, seq_length + 1)
data = np.sin(data_time_steps)
data.resize((seq_length + 1, 1))

x = Variable(torch.Tensor(data[:-1]).type(dtype), requires_grad=False)
y = Variable(torch.Tensor(data[1:]).type(dtype), requires_grad=False)

Eğitim verilerini oluşturacağız, burada x girdi veri dizisi ve y gerekli hedef sıra.

Aşama 3

Ağırlıklar, sıfır ortalama ile normal dağılım kullanılarak tekrarlayan sinir ağında başlatılır. W1, giriş değişkenlerinin kabulünü temsil edecek ve w2, aşağıda gösterildiği gibi üretilen çıktıyı temsil edecektir -

w1 = torch.FloatTensor(input_size, 
hidden_size).type(dtype)
init.normal(w1, 0.0, 0.4)
w1 = Variable(w1, requires_grad = True)
w2 = torch.FloatTensor(hidden_size, output_size).type(dtype)
init.normal(w2, 0.0, 0.3)
w2 = Variable(w2, requires_grad = True)

4. adım

Şimdi, sinir ağını benzersiz bir şekilde tanımlayan ileri besleme için bir işlev oluşturmak önemlidir.

def forward(input, context_state, w1, w2):
   xh = torch.cat((input, context_state), 1)
   context_state = torch.tanh(xh.mm(w1))
   out = context_state.mm(w2)
   return (out, context_state)

Adım 5

Bir sonraki adım, tekrarlayan sinir ağının sinüs dalgası uygulamasının eğitim prosedürüne başlamaktır. Dış döngü, her döngü üzerinde yinelenir ve iç döngü, dizi öğesi boyunca yinelenir. Burada, sürekli değişkenlerin tahminine yardımcı olan Ortalama Kare Hatasını (MSE) de hesaplayacağız.

for i in range(epochs):
   total_loss = 0
   context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = True)
   for j in range(x.size(0)):
      input = x[j:(j+1)]
      target = y[j:(j+1)]
      (pred, context_state) = forward(input, context_state, w1, w2)
      loss = (pred - target).pow(2).sum()/2
      total_loss += loss
      loss.backward()
      w1.data -= lr * w1.grad.data
      w2.data -= lr * w2.grad.data
      w1.grad.data.zero_()
      w2.grad.data.zero_()
      context_state = Variable(context_state.data)
   if i % 10 == 0:
      print("Epoch: {} loss {}".format(i, total_loss.data[0]))

context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = False)
predictions = []

for i in range(x.size(0)):
   input = x[i:i+1]
   (pred, context_state) = forward(input, context_state, w1, w2)
   context_state = context_state
   predictions.append(pred.data.numpy().ravel()[0])

6. Adım

Şimdi, sinüs dalgasını ihtiyaç duyulan şekilde çizme zamanı.

pl.scatter(data_time_steps[:-1], x.data.numpy(), s = 90, label = "Actual")
pl.scatter(data_time_steps[1:], predictions, label = "Predicted")
pl.legend()
pl.show()

Çıktı

Yukarıdaki işlemin çıktısı aşağıdaki gibidir -

Bu bölümde daha fazla odaklanacağız torchvision.datasetsve çeşitli türleri. PyTorch aşağıdaki veri kümesi yükleyicileri içerir -

• MNIST
• COCO (Başlık Oluşturma ve Algılama)

Veri kümesi, aşağıda verilen iki tür işlevin çoğunu içerir -

• Transform- bir görüntüyü alan ve standart öğelerin değiştirilmiş bir sürümünü döndüren bir işlev. Bunlar dönüşümlerle birlikte oluşturulabilir.

• Target_transform- hedefi alan ve dönüştüren bir işlev. Örneğin, başlık dizesini alır ve dünya indekslerinin bir tensörünü döndürür.

MNIST

MNIST veri kümesi için örnek kod aşağıdadır -

dset.MNIST(root, train = TRUE, transform = NONE, 
target_transform = None, download = FALSE)

Parametreler aşağıdaki gibidir -

• root - işlenmiş verilerin bulunduğu veri kümesinin kök dizini.

• train - True = Eğitim seti, Yanlış = Test seti

• download - True = veri setini internetten indirir ve köke yerleştirir.

COCO

Bu, COCO API'nin kurulmasını gerektirir. Aşağıdaki örnek, PyTorch kullanılarak veri kümesinin COCO uygulamasını göstermek için kullanılır -

import torchvision.dataset as dset
import torchvision.transforms as transforms
cap = dset.CocoCaptions(root = ‘ dir where images are’, 
annFile = ’json annotation file’,
transform = transforms.ToTensor())
print(‘Number of samples: ‘, len(cap))
print(target)

Elde edilen çıktı aşağıdaki gibidir -

Number of samples: 82783
Image Size: (3L, 427L, 640L)

Convents, CNN modelini sıfırdan oluşturmakla ilgilidir. Ağ mimarisi, aşağıdaki adımların bir kombinasyonunu içerecektir -

• Conv2d
• MaxPool2d
• Doğrultulmuş Doğrusal Birim
• View
• Doğrusal Katman

Modeli Eğitmek

Modeli eğitmek, görüntü sınıflandırma problemleriyle aynı süreçtir. Aşağıdaki kod parçacığı, sağlanan veri kümesindeki bir eğitim modelinin prosedürünü tamamlar -

def fit(epoch,model,data_loader,phase 
= 'training',volatile = False):
   if phase == 'training':
      model.train()
   if phase == 'training':
      model.train()
   if phase == 'validation':
      model.eval()
   volatile=True
   running_loss = 0.0
   running_correct = 0
   for batch_idx , (data,target) in enumerate(data_loader):
      if is_cuda:
         data,target = data.cuda(),target.cuda()
         data , target = Variable(data,volatile),Variable(target)
      if phase == 'training':
         optimizer.zero_grad()
         output = model(data)
         loss = F.nll_loss(output,target)
         running_loss + = 
         F.nll_loss(output,target,size_average = 
         False).data[0]
         preds = output.data.max(dim = 1,keepdim = True)[1]
         running_correct + = 
         preds.eq(target.data.view_as(preds)).cpu().sum()
         if phase == 'training':
            loss.backward()
            optimizer.step()
   loss = running_loss/len(data_loader.dataset)
   accuracy = 100. * running_correct/len(data_loader.dataset)
   print(f'{phase} loss is {loss:{5}.{2}} and {phase} accuracy is {running_correct}/{len(data_loader.dataset)}{accuracy:{return loss,accuracy}})

Yöntem, eğitim ve doğrulama için farklı mantık içerir. Farklı modları kullanmanın iki ana nedeni vardır -

• Tren modunda, bırakma, doğrulama veya test aşamasında olmaması gereken bir değer yüzdesini kaldırır.

• Eğitim modu için, gradyanları hesaplıyoruz ve modelin parametre değerini değiştiriyoruz, ancak test veya doğrulama aşamalarında geri yayılma gerekli değildir.

Bu bölümde, sıfırdan bir manastır yaratmaya odaklanacağız. Bu, ilgili manastırın veya meşale ile örnek sinir ağının oluşturulmasına neden olur.

Aşama 1

İlgili parametrelerle gerekli bir sınıf oluşturun. Parametreler, rastgele değerli ağırlıkları içerir.

class Neural_Network(nn.Module):
   def __init__(self, ):
      super(Neural_Network, self).__init__()
      self.inputSize = 2
      self.outputSize = 1
      self.hiddenSize = 3
      # weights
      self.W1 = torch.randn(self.inputSize, 
      self.hiddenSize) # 3 X 2 tensor
      self.W2 = torch.randn(self.hiddenSize, self.outputSize) # 3 X 1 tensor

Adım 2

Sigmoid işlevlerle ileri beslemeli bir işlev modeli oluşturun.

def forward(self, X):
   self.z = torch.matmul(X, self.W1) # 3 X 3 ".dot" 
   does not broadcast in PyTorch
   self.z2 = self.sigmoid(self.z) # activation function
   self.z3 = torch.matmul(self.z2, self.W2)
   o = self.sigmoid(self.z3) # final activation 
   function
   return o
   def sigmoid(self, s):
      return 1 / (1 + torch.exp(-s))
   def sigmoidPrime(self, s):
      # derivative of sigmoid
      return s * (1 - s)
   def backward(self, X, y, o):
      self.o_error = y - o # error in output
      self.o_delta = self.o_error * self.sigmoidPrime(o) # derivative of sig to error
      self.z2_error = torch.matmul(self.o_delta, torch.t(self.W2))
      self.z2_delta = self.z2_error * self.sigmoidPrime(self.z2)
      self.W1 + = torch.matmul(torch.t(X), self.z2_delta)
      self.W2 + = torch.matmul(torch.t(self.z2), self.o_delta)

Aşama 3

Aşağıda belirtildiği gibi bir eğitim ve tahmin modeli oluşturun -

def train(self, X, y):
   # forward + backward pass for training
   o = self.forward(X)
   self.backward(X, y, o)
def saveWeights(self, model):
   # Implement PyTorch internal storage functions
   torch.save(model, "NN")
   # you can reload model with all the weights and so forth with:
   # torch.load("NN")
def predict(self):
   print ("Predicted data based on trained weights: ")
   print ("Input (scaled): \n" + str(xPredicted))
   print ("Output: \n" + str(self.forward(xPredicted)))

Evrişimli sinir ağları birincil bir özellik içerir, extraction. Evrişimli sinir ağının özellik çıkarımını uygulamak için aşağıdaki adımlar kullanılır.

Aşama 1

“PyTorch” ile özellik çıkarma modelini oluşturmak için ilgili modelleri içe aktarın.

import torch
import torch.nn as nn
from torchvision import models

Adım 2

Gerektiğinde çağrılabilecek bir özellik çıkarıcı sınıfı oluşturun.

class Feature_extractor(nn.module):
   def forward(self, input):
      self.feature = input.clone()
      return input
new_net = nn.Sequential().cuda() # the new network
target_layers = [conv_1, conv_2, conv_4] # layers you want to extract`
i = 1
for layer in list(cnn):
   if isinstance(layer,nn.Conv2d):
      name = "conv_"+str(i)
      art_net.add_module(name,layer)
      if name in target_layers:
         new_net.add_module("extractor_"+str(i),Feature_extractor())
      i+=1
   if isinstance(layer,nn.ReLU):
      name = "relu_"+str(i)
      new_net.add_module(name,layer)
   if isinstance(layer,nn.MaxPool2d):
      name = "pool_"+str(i)
      new_net.add_module(name,layer)
new_net.forward(your_image)
print (new_net.extractor_3.feature)

Bu bölümde, konvansiyonlar yardımıyla veri görselleştirme modeline odaklanacağız. Geleneksel sinir ağı ile mükemmel bir görselleştirme resmi elde etmek için aşağıdaki adımlar gereklidir.

Aşama 1

Geleneksel sinir ağlarının görselleştirilmesi için önemli olan gerekli modülleri içe aktarın.

import os
import numpy as np
import pandas as pd
from scipy.misc import imread
from sklearn.metrics import accuracy_score

import keras
from keras.models import Sequential, Model
from keras.layers import Dense, Dropout, Flatten, Activation, Input
from keras.layers import Conv2D, MaxPooling2D
import torch

Adım 2

Potansiyel rastgeleliği eğitim ve test verileriyle durdurmak için, aşağıdaki kodda verildiği gibi ilgili veri kümesini arayın -

seed = 128
rng = np.random.RandomState(seed)
data_dir = "../../datasets/MNIST"
train = pd.read_csv('../../datasets/MNIST/train.csv')
test = pd.read_csv('../../datasets/MNIST/Test_fCbTej3.csv')
img_name = rng.choice(train.filename)
filepath = os.path.join(data_dir, 'train', img_name)
img = imread(filepath, flatten=True)

Aşama 3

Aşağıdaki kodu kullanarak mükemmel bir şekilde tanımlanan eğitim ve test verilerini elde etmek için gerekli görüntüleri çizin -

pylab.imshow(img, cmap ='gray')
pylab.axis('off')
pylab.show()

Çıktı aşağıdaki gibi görüntülenir -

Bu bölümde, her iki dizide de tek bir 2D evrişimli sinir ağına dayanan alternatif bir yaklaşım öneriyoruz. Ağımızın her katmanı, şimdiye kadar üretilen çıktı sırasına göre kaynak belirteçlerini yeniden kodlar. Dikkat benzeri özellikler bu nedenle tüm ağda yaygındır.

Burada odaklanacağız creating the sequential network with specific pooling from the values included in dataset. Bu işlem aynı zamanda en iyi "Görüntü Tanıma Modülü" içinde uygulanır.

Aşağıdaki adımlar, PyTorch kullanarak konventlerle bir dizi işleme modeli oluşturmak için kullanılır -

Aşama 1

Sıralı işleme performansı için gerekli modülleri, konvansiyonları kullanarak içe aktarın.

import keras 
from keras.datasets import mnist 
from keras.models import Sequential 
from keras.layers import Dense, Dropout, Flatten 
from keras.layers import Conv2D, MaxPooling2D 
import numpy as np

Adım 2

Aşağıdaki kodu kullanarak ilgili sırayla bir model oluşturmak için gerekli işlemleri gerçekleştirin -

batch_size = 128 
num_classes = 10 
epochs = 12
# input image dimensions 
img_rows, img_cols = 28, 28
# the data, split between train and test sets 
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000,28,28,1) 
x_test = x_test.reshape(10000,28,28,1)
print('x_train shape:', x_train.shape) 
print(x_train.shape[0], 'train samples') 
print(x_test.shape[0], 'test samples')
y_train = keras.utils.to_categorical(y_train, num_classes) 
y_test = keras.utils.to_categorical(y_test, num_classes)

Aşama 3

Modeli derleyin ve modeli aşağıda gösterildiği gibi belirtilen geleneksel sinir ağı modeline uydurun -

model.compile(loss = 
keras.losses.categorical_crossentropy, 
optimizer = keras.optimizers.Adadelta(), metrics = 
['accuracy'])
model.fit(x_train, y_train, 
batch_size = batch_size, epochs = epochs, 
verbose = 1, validation_data = (x_test, y_test)) 
score = model.evaluate(x_test, y_test, verbose = 0) 
print('Test loss:', score[0]) 
print('Test accuracy:', score[1])

Üretilen çıktı aşağıdaki gibidir -

Bu bölümde, ünlü kelime yerleştirme modelini anlayacağız - word2vec. Word2vec modeli, ilgili modeller grubu yardımıyla kelime gömme üretmek için kullanılır. Word2vec modeli saf C kodu ile uygulanır ve gradyan manuel olarak hesaplanır.

PyTorch'ta word2vec modelinin uygulanması aşağıdaki adımlarda açıklanmaktadır -

Aşama 1

Kitaplıkları aşağıda belirtildiği gibi kelime gömme olarak uygulayın -

import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F

Adım 2

Kelime yerleştirmenin Skip Gram Modelini word2vec adlı sınıfla uygulayın. O içeriremb_size, emb_dimension, u_embedding, v_embedding özniteliklerin türü.

class SkipGramModel(nn.Module):
   def __init__(self, emb_size, emb_dimension):
      super(SkipGramModel, self).__init__()
      self.emb_size = emb_size
      self.emb_dimension = emb_dimension
      self.u_embeddings = nn.Embedding(emb_size, emb_dimension, sparse=True)
      self.v_embeddings = nn.Embedding(emb_size, emb_dimension, sparse = True)
      self.init_emb()
   def init_emb(self):
      initrange = 0.5 / self.emb_dimension
      self.u_embeddings.weight.data.uniform_(-initrange, initrange)
      self.v_embeddings.weight.data.uniform_(-0, 0)
   def forward(self, pos_u, pos_v, neg_v):
      emb_u = self.u_embeddings(pos_u)
      emb_v = self.v_embeddings(pos_v)
      score = torch.mul(emb_u, emb_v).squeeze()
      score = torch.sum(score, dim = 1)
      score = F.logsigmoid(score)
      neg_emb_v = self.v_embeddings(neg_v)
      neg_score = torch.bmm(neg_emb_v, emb_u.unsqueeze(2)).squeeze()
      neg_score = F.logsigmoid(-1 * neg_score)
      return -1 * (torch.sum(score)+torch.sum(neg_score))
   def save_embedding(self, id2word, file_name, use_cuda):
      if use_cuda:
         embedding = self.u_embeddings.weight.cpu().data.numpy()
      else:
         embedding = self.u_embeddings.weight.data.numpy()
      fout = open(file_name, 'w')
      fout.write('%d %d\n' % (len(id2word), self.emb_dimension))
      for wid, w in id2word.items():
         e = embedding[wid]
         e = ' '.join(map(lambda x: str(x), e))
         fout.write('%s %s\n' % (w, e))
def test():
   model = SkipGramModel(100, 100)
   id2word = dict()
   for i in range(100):
      id2word[i] = str(i)
   model.save_embedding(id2word)

Aşama 3

Doğru şekilde görüntülenen kelime yerleştirme modelini elde etmek için ana yöntemi uygulayın.

if __name__  ==  '__main__':
   test()

Derin sinir ağları, makine öğreniminde doğal dil sürecini anlamada atılımlar sağlayan özel bir özelliğe sahiptir. Bu modellerin çoğunun dili düz bir kelime veya karakter dizisi olarak ele aldığı ve tekrarlayan sinir ağı veya RNN olarak adlandırılan bir tür model kullandığı gözlemlenmiştir.

Pek çok araştırmacı, dilin en iyi hiyerarşik ifadeler ağacına göre anlaşıldığı sonucuna varmıştır. Bu tür, belirli bir yapıyı hesaba katan özyinelemeli sinir ağlarına dahildir.

PyTorch, bu karmaşık doğal dil işleme modellerini çok daha kolay hale getirmeye yardımcı olan belirli bir özelliğe sahiptir. Bilgisayarla görü için güçlü destek ile her türlü derin öğrenme için tam özellikli bir çerçevedir.

Özyinelemeli Sinir Ağının Özellikleri

• Özyinelemeli bir sinir ağı, farklı grafik benzeri yapılarla aynı ağırlık kümesinin uygulanmasını içerecek şekilde oluşturulur.

• Düğümler topolojik sırayla geçilir.

• Bu tür bir ağ, otomatik farklılaşmanın ters modu ile eğitilir.

• Doğal dil işleme, özel bir yinelemeli sinir ağları durumu içerir.

• Bu yinelemeli sinir tensör ağı, ağaçtaki çeşitli bileşim fonksiyonel düğümlerini içerir.

Yinelemeli sinir ağı örneği aşağıda gösterilmiştir -