VLSI Tasarımı - MOS Transistör
Tamamlayıcı MOSFET (CMOS) teknolojisi, günümüzde çok sayıda ve çeşitli uygulamalarda devreler oluşturmak için yaygın olarak kullanılmaktadır. Günümüzün bilgisayarları, CPU'ları ve cep telefonları, çeşitli temel avantajlardan dolayı CMOS'u kullanır. CMOS, her iki durumda da düşük güç dağılımı, nispeten yüksek hız, yüksek gürültü marjları sunar ve çok çeşitli kaynak ve giriş voltajlarında çalışır (kaynak voltajının sabit olması şartıyla)
Tartışacağımız süreçler için, mevcut transistör türü Metal Oksit-Yarı İletken Alan Etkili Transistördür (MOSFET). Bu transistörler oluşturulduas a ‘sandwich’tek bir silikon kristalinden bir yarı iletken katmandan, genellikle bir dilim veya tabakadan oluşur; bir silikon dioksit tabakası (oksit) ve bir metal tabaka.
Bir MOSFET'in Yapısı
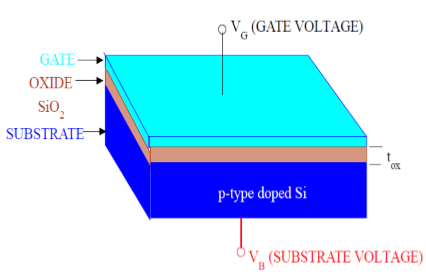
Şekilde gösterildiği gibi, MOS yapısı üç katman içerir -
The Metal Gate Electrode
The Insulating Oxide Layer (SiO2)
P – type Semiconductor (Substrate)
MOS yapısı, bir kondansatör oluşturur, geçit ve alt tabaka dielektrik malzeme olarak iki plaka ve oksit tabakasıdır. Dielektrik malzemenin (SiO 2 ) kalınlığı genellikle 10 nm ile 50 nm arasındadır. Taşıyıcı konsantrasyonu ve alt tabaka içindeki dağılımı, kapı ve alt tabaka terminaline uygulanan harici voltajla değiştirilebilir. Şimdi, MOS'un yapısını anlamak için, önce P - Tipi yarı iletken substratın temel elektrik özelliklerini düşünün.
Taşıyıcının yarı iletken malzemedeki konsantrasyonu her zaman aşağıdaki Mass Action Law. Kitle Eylem Yasası şu şekilde verilir -
$$ np = n_ {i} ^ {2} $$
Nerede,
n elektronların taşıyıcı konsantrasyonu
p deliklerin taşıyıcı konsantrasyonu
ni Silikonun iç taşıyıcı konsantrasyonudur
Şimdi, substratın alıcı (Boron) konsantrasyonu N A ile eşit derecede katkılı olduğunu varsayalım . Dolayısıyla, p tipi substrattaki elektron ve delik konsantrasyonu
$$ n_ {po} = \ frac {n_ {i} ^ {2}} {N_ {A}} $$
$$ p_ {po} = N_ {A} $$
Burada doping konsantrasyonu NAintrinsik konsantrasyon n'den (10 15 ila 10 16 cm- 3 ) daha büyüktür. Şimdi, MOS yapısını anlamak için, p tipi silikon substratın enerji seviyesi diyagramını düşünün.
Şekilde gösterildiği gibi, iletim bandı ile değerlik bandı arasındaki bant aralığı 1.1eV'dir. Burada, Fermi potansiyeli Φ F , içsel Fermi seviyesi (E i ) ve Fermi seviyesi (E FP ) arasındaki farktır .
Fermi seviyesi E F'nin doping konsantrasyonuna bağlı olduğu durumlarda. Fermi potansiyeli Φ F , içsel Fermi seviyesi (E i ) ve Fermi seviyesi (E FP ) arasındaki farktır .
Matematiksel olarak,
$$ \ Phi_ {Fp} = \ frac {E_ {F} -E_ {i}} {q} $$
İletim bandı ile boş alan arasındaki potansiyel farka elektron afinitesi denir ve qx ile gösterilir.
Dolayısıyla, bir elektronun Fermi seviyesinden boş uzaya geçmesi için gereken enerjiye iş fonksiyonu (qΦ S ) denir ve
$$ q \ Phi _ {s} = (E_ {c} -E_ {F}) + qx $$
Aşağıdaki şekil, MOS'u oluşturan bileşenlerin enerji bandı diyagramını göstermektedir.
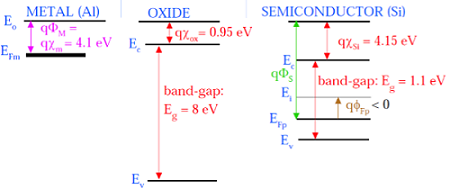
Kalıntı yalıtım yukarıdaki şekilde gösterildiği gibi, 2 kat 8eV büyük enerji bant boşluk vardır ve çalışma fonksiyonu 0.95 eV'dir. Metal kapı 4.1eV çalışma fonksiyonuna sahiptir. Burada, iş fonksiyonları farklıdır, bu nedenle MOS sisteminde voltaj düşüşü yaratacaktır. Aşağıda verilen şekil, MOS sisteminin birleşik enerji bandı diyagramını göstermektedir.
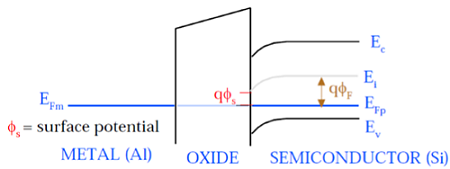
Bu şekilde gösterildiği gibi, metal geçit ve yarı iletken (Si) fermi potansiyel seviyesi aynı potansiyeldedir. Yüzeydeki Fermi potansiyeline yüzey potansiyeli Φ S denir ve büyüklük olarak Fermi potansiyeli Φ F'den daha küçüktür .
Bir MOSFET'in Çalışması
MOSFET, kanal bölgesine kapalı olarak yerleştirilmiş iki pn bağlantılı bir MOS kapasitöründen oluşur ve bu bölge kapı voltajı ile kontrol edilir. Her iki pn birleşimini ters taraflı yapmak için substrat potansiyeli diğer üç terminal potansiyelinden daha düşük tutulur.
Kapı voltajı eşik voltajının (V GS > V TO ) ötesine yükseltilecekse , yüzeyde ters çevirme tabakası oluşacak ve kaynak ile drenaj arasında n tipi kanal oluşacaktır. Bu n tipi kanal, boşaltma akımını V DS değerine göre taşıyacaktır .
Farklı V DS değerleri için , MOSFET aşağıda açıklandığı gibi farklı bölgelerde çalıştırılabilir.
Doğrusal Bölge
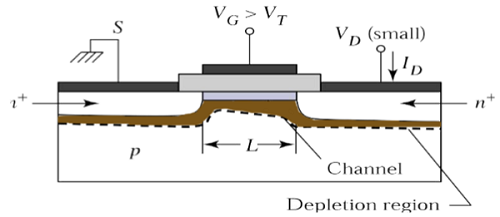
V DS = 0'da, ters çevrilmiş kanal bölgesinde termal denge vardır ve boşaltma akımı I D = 0'dır. Şimdi, eğer küçük boşaltma gerilimi, V DS > 0 uygulanırsa, V DS ile orantılı bir boşaltma akımı kaynaktan akmaya başlayacaktır. kanaldan boşaltın.
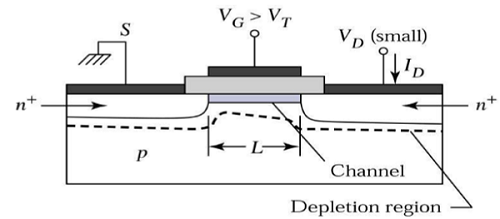
Kanal, kaynaktan drenaja akım akışı için sürekli bir yol sağlar. Bu çalışma moduna denirlinear region. Doğrusal bölgede çalışan bir n-kanallı MOSFET'in enine kesit görünümü, aşağıda verilen şekilde gösterilmektedir.
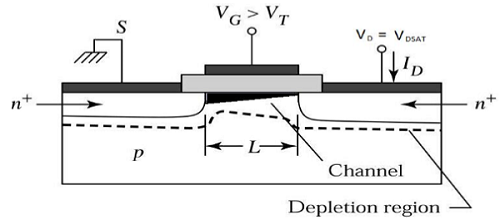
Doygunluk Bölgesinin Kenarında
Şimdi V DS artırılırsa, kanaldaki yükler ve kanal derinliği boşaltma sonunda azalır. V DS = V DSAT için , kanaldaki ücretler sıfıra düşürülür ve buna denirpinch – off point. Doygunluk bölgesinin kenarında çalışan n-kanallı MOSFET'in enine kesit görünümü aşağıdaki şekilde gösterilmektedir.
Doygunluk Bölgesi
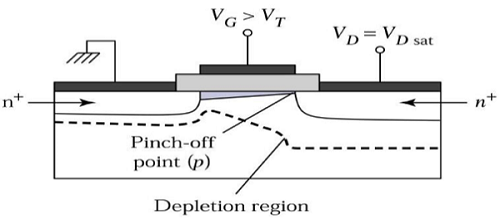
V DS > V DSAT için , boşaltma noktasına yakın tükenmiş bir yüzey oluşur ve boşaltma voltajını artırarak bu tükenmiş bölge kaynağa kadar uzanır.
Bu çalışma moduna denir Saturation region. Kaynaktan kanal ucuna gelen elektronlar drenaj - tükenme bölgesine girerek yüksek elektrik alanında drenaja doğru hızlanırlar.
MOSFET Akım - Gerilim Karakteristikleri
MOSFET'in akım - voltaj karakteristiğini anlamak için kanal için yaklaşım yapılır. Bu yaklaşım olmadan, MOS sisteminin üç boyutlu analizi karmaşık hale gelir. Gradual Channel Approximation (GCA) akım - gerilim karakteristiği için analiz problemini azaltacaktır.
Kademeli Kanal Yaklaşımı (GCA)
Doğrusal modda çalışan n kanallı MOSFET'in enine kesit görünümünü düşünün. Burada kaynak ve alt tabaka zemine bağlanır. V S = V B = 0. Kapıdan kaynağa (V GS ) ve boşaltmadan kaynağa voltaj (V DS ) voltajı, boşaltma akımını I D kontrol eden harici parametrelerdir .
Voltaj, V GS , kaynak ve boşaltma arasında bir kanal oluşturmak için, V TO eşik voltajından daha büyük bir voltaja ayarlanır . Şekilde görüldüğü gibi x yönü yüzeye dik ve y yönü yüzeye paraleldir.
Burada, şekilde gösterildiği gibi kaynak ucunda y = 0. Kaynağa göre kanal voltajı şu şekilde temsil edilir:VC(Y). VTO eşik voltajının y = 0 ile y = L arasında kanal bölgesi boyunca sabit olduğunu varsayın. Kanal voltajı V C için sınır koşulu -
$$ V_ {c} \ left (y = 0 \ sağ) = V_ {s} = 0 \ ve \, V_ {c} \ left (y = L \ sağ) = V_ {DS} $$
Ayrıca varsayabiliriz ki
$$ V_ {GS} \ geq V_ {TO} $$ ve
$$ V_ {GD} = V_ {GS} -V_ {DS} \ geq V_ {TO} $$
Q1 (y), yüzey ters çevirme katmanındaki toplam mobil elektron yükü olsun. Bu elektron yükü şu şekilde ifade edilebilir:
$$ Q1 (y) = - C_ {öküz}. [V_ {GS} -V_ {C (Y)} - V_ {TO}] $$
Aşağıda verilen şekil, yüzey ters çevirme katmanının uzamsal geometrisini gösterir ve boyutlarını belirtir. Drenajdan kaynağa geçerken ters çevirme tabakası incelir. Şimdi, L kanal uzunluğunun küçük bölgesi dy'yi düşünürsek, bu bölge tarafından sunulan artan direnç dR şu şekilde ifade edilebilir
$$ dR = - \ frac {dy} {w. \ mu _ {n} .Q1 (y)} $$
Burada, eksi işareti nedeniyle ters tabaka yük Q1 negatif polariteye ve μ n sabit yüzey hareket vardır. Şimdi, dR denklemindeki Q1 (y) değerini değiştirin -
$$ dR = - \ frac {dy} {w. \ mu _ {n}. \ left \ {-C_ {ox} \ left [V_ {GS} -V_ {C \ left (Y \ sağ)} \ sağ ] -V_ {TO} \ right \}} $$
$$ dR = \ frac {dy} {w. \ mu _ {n} .C_ {ox} \ left [V_ {GS} -V_ {C \ left (Y \ sağ)} \ sağ] -V_ {TO} } $$
Şimdi küçük dy bölgesindeki voltaj düşüşü şu şekilde verilebilir:
$$ dV_ {c} = I_ {D} .dR $$
DR'nin değerini yukarıdaki denkleme koyun
$$ dV_ {C} = I_ {D}. \ frac {dy} {w. \ mu_ {n} .C_ {ox} \ left [V_ {GS} -V_ {C (Y)} \ sağ] -V_ {TO}} $$
$$ w. \ mu _ {n} .C_ {öküz} \ sol [V_ {GS} -V_ {C (Y)} - V_ {TO} \ sağ] .dV_ {C} = I_ {D} .dy $$
Tüm kanal bölgesi üzerinden boşaltma akımı ID'sini elde etmek için, yukarıdaki denklem kanal boyunca y = 0'dan y = L'ye ve V C (y) = 0'dan V C (y) = V DS'ye kadar entegre edilebilir ,
$$ C_ {ox} .w. \ Mu _ {n}. \ İnt_ {V_ {c} = 0} ^ {V_ {DS}} \ left [V_ {GS} -V_ {C \ left (Y \ sağ )} - V_ {TO} \ sağ] .dV_ {C} = \ int_ {Y = 0} ^ {L} I_ {D} .dy $$
$$ \ frac {C_ {ox} .w. \ mu _ {n}} {2} \ left (2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ sağ) = I_ {D} \ sol [L-0 \ sağ] $$
$$ I_ {D} = \ frac {C_ {ox}. \ Mu _ {n}} {2}. \ Frac {w} {L} \ left (2 \ left [V_ {GS} -V_ {TO} \ sağ] V_ {DS} -V_ {DS} ^ {2} \ sağ) $$
Doğrusal bölge V DS <V GS - V TO için . Doygunluk bölgesi için, V DS değeri (V GS - V TO ) ' dan büyüktür . Bu nedenle, doygunluk bölgesi için V DS = (V GS - V TO ).
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {\ left [2V_ {DS} \ right] V_ {DS} -V_ { DS} ^ {2}} {L} \ sağ) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {2V_ {DS} ^ {2} -V_ {DS} ^ {2} } {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {V_ {DS} ^ {2}} {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {\ left [V_ {GS} -V_ {TO} \ sağ] ^ { 2}} {L} \ sağ) $$