Học hỏi và Thích nghi
Như đã nói trước đó, ANN hoàn toàn được lấy cảm hứng từ cách hệ thống thần kinh sinh học, tức là bộ não con người hoạt động. Đặc điểm ấn tượng nhất của bộ não con người là học hỏi, do đó ANN có được tính năng tương tự.
Học trong ANN là gì?
Về cơ bản, học tập có nghĩa là thực hiện và thích ứng với sự thay đổi của chính nó khi có sự thay đổi trong môi trường. ANN là một hệ thống phức tạp hay chính xác hơn chúng ta có thể nói rằng nó là một hệ thống thích ứng phức tạp, có thể thay đổi cấu trúc bên trong của nó dựa trên thông tin đi qua nó.
Tại sao nó lại quan trọng?
Là một hệ thống thích ứng phức tạp, học trong ANN ngụ ý rằng một đơn vị xử lý có khả năng thay đổi hành vi đầu vào / đầu ra của nó do sự thay đổi của môi trường. Tầm quan trọng của việc học trong ANN tăng lên do chức năng kích hoạt cố định cũng như vector đầu vào / đầu ra, khi một mạng cụ thể được xây dựng. Bây giờ để thay đổi hành vi đầu vào / đầu ra, chúng ta cần điều chỉnh trọng số.
Phân loại
Nó có thể được định nghĩa là quá trình học cách phân biệt dữ liệu của các mẫu thành các lớp khác nhau bằng cách tìm ra các đặc điểm chung giữa các mẫu của cùng các lớp. Ví dụ: để thực hiện đào tạo ANN, chúng tôi có một số mẫu đào tạo với các tính năng độc đáo và để thực hiện kiểm tra, chúng tôi có một số mẫu thử nghiệm với các tính năng độc đáo khác. Phân loại là một ví dụ về học có giám sát.
Quy tắc học tập mạng thần kinh
Chúng tôi biết rằng, trong quá trình học ANN, để thay đổi hành vi đầu vào / đầu ra, chúng tôi cần điều chỉnh trọng số. Do đó, cần có một phương pháp với sự trợ giúp của trọng số có thể được sửa đổi. Các phương pháp này được gọi là Học quy tắc, đơn giản là các thuật toán hoặc phương trình. Sau đây là một số quy tắc học tập cho mạng nơ-ron:
Quy tắc học tiếng Hebbian
Quy tắc này, một trong những quy tắc lâu đời nhất và đơn giản nhất, đã được Donald Hebb giới thiệu trong cuốn sách Tổ chức các hành vi của ông vào năm 1949. Đây là một kiểu học tập tiến lên, không giám sát.
Basic Concept - Quy tắc này dựa trên một đề xuất do Hebb đưa ra, người đã viết -
“Khi một sợi trục của tế bào A ở gần đủ để kích thích tế bào B và liên tục hoặc liên tục tham gia vào quá trình kích hoạt nó, một số quá trình tăng trưởng hoặc thay đổi trao đổi chất diễn ra ở một hoặc cả hai tế bào sao cho hiệu quả của tế bào A, khi một trong các tế bào bắn ra B , được tăng lên. ”
Từ định đề trên, chúng ta có thể kết luận rằng các kết nối giữa hai tế bào thần kinh có thể được củng cố nếu các tế bào thần kinh hoạt động cùng một lúc và có thể yếu đi nếu chúng hoạt động vào những thời điểm khác nhau.
Mathematical Formulation - Theo quy tắc học Hebbian, sau đây là công thức để tăng trọng số của kết nối tại mỗi bước thời gian.
$$ \ Delta w_ {ji} (t) \: = \: \ alpha x_ {i} (t) .y_ {j} (t) $$
Ở đây, $ \ Delta w_ {ji} (t) $ = gia số theo đó trọng lượng của kết nối tăng lên tại bước thời gian t
$ \ alpha $ = tỷ lệ học tập tích cực và liên tục
$ x_ {i} (t) $ = giá trị đầu vào từ nơ-ron tiền synap ở bước thời gian t
$ y_ {i} (t) $ = đầu ra của nơ-ron tiền synap ở cùng một bước t
Quy tắc học tập Perceptron
Quy tắc này là một lỗi sửa chữa thuật toán học có giám sát của các mạng truyền thẳng lớp đơn với chức năng kích hoạt tuyến tính, được giới thiệu bởi Rosenblatt.
Basic Concept- Bản chất là được giám sát, để tính toán sai số, sẽ có sự so sánh giữa đầu ra mong muốn / mục tiêu và đầu ra thực tế. Nếu có bất kỳ sự khác biệt nào được tìm thấy, thì phải thực hiện thay đổi đối với trọng số của kết nối.
Mathematical Formulation - Để giải thích công thức toán học của nó, giả sử chúng ta có 'n' số vectơ đầu vào hữu hạn, x (n), cùng với vectơ đầu ra mong muốn / đích của nó t (n), trong đó n = 1 đến N.
Bây giờ đầu ra 'y' có thể được tính toán, như đã giải thích trước đó trên cơ sở đầu vào ròng và chức năng kích hoạt đang được áp dụng trên đầu vào ròng đó có thể được biểu thị như sau:
$$ y \: = \: f (y_ {in}) \: = \: \ begin {case} 1, & y_ {in} \:> \: \ theta \\ 0, & y_ {in} \: \ leqslant \: \ theta \ end {case} $$
Ở đâu θ là ngưỡng.
Việc cập nhật trọng lượng có thể được thực hiện trong hai trường hợp sau:
Case I - khi nào t ≠ y, sau đó
$$ w (mới) \: = \: w (cũ) \: + \; tx $$
Case II - khi nào t = y, sau đó
Không thay đổi trọng lượng
Quy tắc học tập Delta (Quy tắc Widrow-Hoff)
Nó được giới thiệu bởi Bernard Widrow và Marcian Hoff, còn được gọi là phương pháp Least Mean Square (LMS), để giảm thiểu sai số trên tất cả các mẫu huấn luyện. Nó là một loại thuật toán học có giám sát với chức năng kích hoạt liên tục.
Basic Concept- Cơ sở của quy tắc này là phương pháp tiếp cận giảm dần độ dốc, tiếp cận mãi mãi. Quy tắc Delta cập nhật trọng số của khớp thần kinh để giảm thiểu đầu vào ròng cho đơn vị đầu ra và giá trị đích.
Mathematical Formulation - Để cập nhật trọng số synap, quy tắc delta được đưa ra bởi
$$ \ Delta w_ {i} \: = \: \ alpha \:. X_ {i} .e_ {j} $$
Đây $ \ Delta w_ {i} $ = thay đổi trọng lượng cho thứ pattern của tôi ;
$ \ alpha $ = tỷ lệ học tập tích cực và liên tục;
$ x_ {i} $ = giá trị đầu vào từ nơ-ron trước synap;
$ e_ {j} $ = $ (t \: - \: y_ {in}) $, sự khác biệt giữa đầu ra mong muốn / mục tiêu và đầu ra thực tế $ y_ {in} $
Quy tắc delta ở trên chỉ dành cho một đơn vị đầu ra duy nhất.
Việc cập nhật trọng lượng có thể được thực hiện trong hai trường hợp sau:
Case-I - khi nào t ≠ y, sau đó
$$ w (mới) \: = \: w (cũ) \: + \: \ Delta w $$
Case-II - khi nào t = y, sau đó
Không thay đổi trọng lượng
Quy tắc học tập cạnh tranh (Người chiến thắng-giành-tất cả)
Nó liên quan đến việc đào tạo không có giám sát, trong đó các nút đầu ra cố gắng cạnh tranh với nhau để đại diện cho mẫu đầu vào. Để hiểu quy tắc học tập này, chúng ta phải hiểu mạng cạnh tranh được đưa ra như sau:
Basic Concept of Competitive Network- Mạng này giống như một mạng chuyển tiếp một lớp với kết nối phản hồi giữa các đầu ra. Các kết nối giữa các đầu ra là kiểu ức chế, được thể hiện bằng các đường chấm, có nghĩa là các đối thủ không bao giờ hỗ trợ mình.
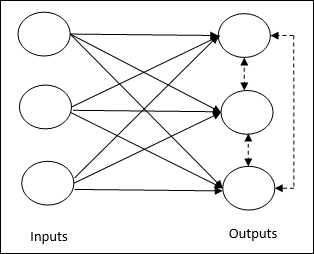
Basic Concept of Competitive Learning Rule- Như đã nói trước đó, sẽ có sự cạnh tranh giữa các nút đầu ra. Do đó, khái niệm chính là trong quá trình đào tạo, đơn vị đầu ra có độ kích hoạt cao nhất đối với một mẫu đầu vào nhất định, sẽ được tuyên bố là người chiến thắng. Quy tắc này còn được gọi là Winner-take-all vì chỉ có nơ-ron chiến thắng được cập nhật và các nơ-ron còn lại không thay đổi.
Mathematical formulation - Sau đây là ba yếu tố quan trọng để lập công thức toán học của quy tắc học tập này -
Condition to be a winner - Giả sử nếu một nơron $ y_ {k} $ muốn trở thành người chiến thắng thì sẽ có điều kiện sau:
$$ y_ {k} \: = \: \ begin {case} 1 & if \: v_ {k} \:> \: v_ {j} \: cho \: tất cả \: j, \: j \: \ neq \: k \\ 0 và nếu không thì \ end {case} $$
Có nghĩa là nếu bất kỳ nơ-ron nào, chẳng hạn $ y_ {k} $ , muốn chiến thắng, thì trường cục bộ cảm ứng của nó (đầu ra của đơn vị tính tổng), ví dụ $ v_ {k} $, phải lớn nhất trong số tất cả các nơ-ron khác trong mạng.
Condition of sum total of weight - Một hạn chế khác đối với quy tắc học cạnh tranh là, tổng trọng số của một nơ-ron đầu ra cụ thể sẽ là 1. Ví dụ, nếu chúng ta xem xét nơ-ron k sau đó -
$$ \ displaystyle \ sum \ limit_ {j} w_ {kj} \: = \: 1 \: \: \: \: \: \: \: \: \: \: cho \: tất cả \: k $$
Change of weight for winner- Nếu một tế bào thần kinh không đáp ứng với mẫu đầu vào, thì không có học tập nào diễn ra trong tế bào thần kinh đó. Tuy nhiên, nếu một nơron cụ thể thắng, thì trọng số tương ứng được điều chỉnh như sau
$$ \ Delta w_ {kj} \: = \: \ begin {case} - \ alpha (x_ {j} \: - \: w_ {kj}) và if \: neuron \: k \: win \\ 0, & if \: neuron \: k \: lỗ \ end {case} $$
Đây $ \ alpha $ là tỷ lệ học tập.
Điều này cho thấy rõ ràng rằng chúng ta đang ủng hộ nơ-ron chiến thắng bằng cách điều chỉnh trọng lượng của nó và nếu nơ-ron bị mất đi, thì chúng ta không cần phải điều chỉnh lại trọng lượng của nó.
Quy tắc học tập Outstar
Quy tắc này, do Grossberg đưa ra, liên quan đến việc học có giám sát vì các kết quả đầu ra mong muốn đã được biết trước. Nó còn được gọi là học Grossberg.
Basic Concept- Quy tắc này được áp dụng trên các tế bào thần kinh được sắp xếp trong một lớp. Nó được thiết kế đặc biệt để tạo ra đầu ra mong muốnd của lớp p tế bào thần kinh.
Mathematical Formulation - Các điều chỉnh trọng lượng trong quy tắc này được tính như sau
$$ \ Delta w_ {j} \: = \: \ alpha \ :( d \: - \: w_ {j}) $$
Đây d là đầu ra nơ-ron mong muốn và $ \ alpha $ là tốc độ học.