Học tập không giám sát

Như tên cho thấy, loại hình học tập này được thực hiện mà không có sự giám sát của giáo viên. Quá trình học tập này là độc lập. Trong quá trình đào tạo ANN dưới sự học tập không giám sát, các vectơ đầu vào cùng loại được kết hợp để tạo thành các cụm. Khi một mẫu đầu vào mới được áp dụng, thì mạng nơ ron sẽ đưa ra phản hồi đầu ra cho biết lớp mà mẫu đầu vào thuộc về. Trong điều này, sẽ không có phản hồi từ môi trường về những gì nên là đầu ra mong muốn và liệu nó đúng hay sai. Do đó, trong kiểu học này, bản thân mạng phải khám phá ra các mẫu, các tính năng từ dữ liệu đầu vào và mối quan hệ giữa dữ liệu đầu vào với đầu ra.

Người chiến thắng-giành-tất cả các mạng

Các loại mạng này dựa trên quy tắc học tập cạnh tranh và sẽ sử dụng chiến lược trong đó nó chọn nơ-ron có tổng đầu vào lớn nhất làm người chiến thắng. Các kết nối giữa các nơ-ron đầu ra cho thấy sự cạnh tranh giữa chúng và một trong số chúng sẽ là 'BẬT' có nghĩa là nó sẽ là người chiến thắng và những tế bào khác sẽ là 'TẮT'.

Sau đây là một số mạng dựa trên khái niệm đơn giản này bằng cách sử dụng phương pháp học không giám sát.

Mạng lưới Hamming

Trong hầu hết các mạng nơ-ron sử dụng phương pháp học không giám sát, điều cần thiết là phải tính khoảng cách và thực hiện so sánh. Loại mạng này là mạng Hamming, trong đó đối với mỗi vectơ đầu vào nhất định, nó sẽ được nhóm lại thành các nhóm khác nhau. Sau đây là một số tính năng quan trọng của Hamming Networks:

Lippmann bắt đầu làm việc trên mạng Hamming vào năm 1987.
Nó là một mạng một lớp.
Các đầu vào có thể là nhị phân {0, 1} của lưỡng cực {-1, 1}.
Trọng lượng của lưới được tính bằng các vectơ mẫu.
Nó là một mạng lưới trọng lượng cố định có nghĩa là trọng lượng sẽ không thay đổi ngay cả trong khi tập luyện.

Mạng tối đa

Đây cũng là một mạng trọng số cố định, đóng vai trò như một mạng con để chọn nút có đầu vào cao nhất. Tất cả các nút được kết nối hoàn toàn với nhau và tồn tại các trọng số đối xứng trong tất cả các kết nối có trọng số này.

Ngành kiến trúc

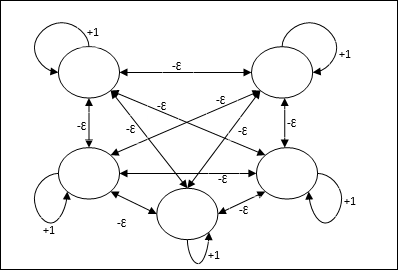
Nó sử dụng cơ chế là một quá trình lặp đi lặp lại và mỗi nút nhận đầu vào ức chế từ tất cả các nút khác thông qua các kết nối. Nút duy nhất có giá trị lớn nhất sẽ hoạt động hoặc chiến thắng và các kích hoạt của tất cả các nút khác sẽ không hoạt động. Max Net sử dụng chức năng kích hoạt danh tính với $$ f (x) \: = \: \ begin {case} x & if \: x> 0 \\ 0 & if \: x \ leq 0 \ end {case} $$

Nhiệm vụ của mạng này được thực hiện nhờ trọng lượng tự kích thích +1 và cường độ ức chế lẫn nhau, được đặt như [0 <ɛ <$ \ frac {1} {m} $] trong đó “m” là tổng số nút.

Học tập cạnh tranh trong ANN

Nó liên quan đến việc đào tạo không có giám sát, trong đó các nút đầu ra cố gắng cạnh tranh với nhau để đại diện cho mẫu đầu vào. Để hiểu quy tắc học tập này, chúng ta sẽ phải hiểu mạng lưới cạnh tranh được giải thích như sau:

Khái niệm cơ bản về mạng lưới cạnh tranh

Mạng này giống như một mạng chuyển tiếp cấp một lớp có kết nối phản hồi giữa các đầu ra. Các kết nối giữa các đầu ra là kiểu ức chế, được thể hiện bằng các đường chấm, có nghĩa là các đối thủ cạnh tranh không bao giờ hỗ trợ mình.

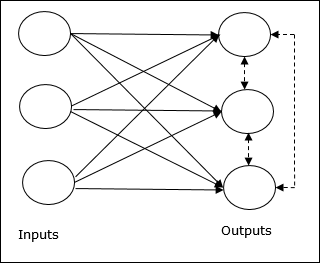
Khái niệm cơ bản về Quy tắc học tập cạnh tranh

Như đã nói trước đó, sẽ có sự cạnh tranh giữa các nút đầu ra vì vậy khái niệm chính là - trong quá trình đào tạo, đơn vị đầu ra có kích hoạt cao nhất đối với một mẫu đầu vào nhất định, sẽ được tuyên bố là người chiến thắng. Quy tắc này còn được gọi là Winner-take-all vì chỉ có nơ-ron chiến thắng được cập nhật và các nơ-ron còn lại không thay đổi.

Công thức toán học

Sau đây là ba yếu tố quan trọng để xây dựng công thức toán học của quy tắc học tập này:

Điều kiện để trở thành người chiến thắng

Giả sử nếu một tế bào thần kinh y_k muốn trở thành người chiến thắng thì cần có điều kiện sau

$$ y_ {k} \: = \: \ begin {case} 1 & if \: v_ {k}> v_ {j} \: for \: all \: \: j, \: j \: \ neq \ : k \\ 0 và nếu không thì \ end {case} $$

Có nghĩa là nếu bất kỳ nơron nào, y_k muốn giành chiến thắng, thì trường cục bộ gây ra của nó (đầu ra của đơn vị tổng hợp), nói v_k, phải lớn nhất trong số tất cả các nơ-ron khác trong mạng.
Điều kiện của tổng trọng lượng

Một hạn chế khác đối với quy tắc học tập cạnh tranh là tổng trọng số của một nơ-ron đầu ra cụ thể sẽ là 1. Ví dụ, nếu chúng ta xem xét nơ-ron k sau đó

$$ \ displaystyle \ sum \ limit_ {k} w_ {kj} \: = \: 1 \: \: \: \: cho \: tất cả \: \: k $$
Thay đổi trọng lượng cho người chiến thắng

Nếu một tế bào thần kinh không đáp ứng với mẫu đầu vào, thì sẽ không có hoạt động học nào diễn ra trong tế bào thần kinh đó. Tuy nhiên, nếu một nơ-ron cụ thể thắng, thì trọng số tương ứng được điều chỉnh như sau:

$$ \ Delta w_ {kj} \: = \: \ begin {case} - \ alpha (x_ {j} \: - \: w_ {kj}) và if \: neuron \: k \: win \\ 0 & if \: neuron \: k \: lỗ \ end {case} $$

Đây $ \ alpha $ là tỷ lệ học tập.

Điều này cho thấy rõ ràng rằng chúng ta đang ủng hộ nơ-ron chiến thắng bằng cách điều chỉnh trọng lượng của nó và nếu một nơ-ron bị mất, chúng ta không cần phải điều chỉnh lại trọng lượng của nó.

K-means Clustering Algorithm

K-mean là một trong những thuật toán phân cụm phổ biến nhất mà chúng ta sử dụng khái niệm thủ tục phân vùng. Chúng tôi bắt đầu với một phân vùng ban đầu và liên tục di chuyển các mẫu từ cụm này sang cụm khác, cho đến khi chúng tôi nhận được kết quả ưng ý.

Thuật toán

Step 1 - Chọn kđiểm như là trung tâm ban đầu. Khởi tạok nguyên mẫu (w₁,…,w_k), ví dụ, chúng ta có thể xác định chúng bằng các vectơ đầu vào được chọn ngẫu nhiên -

$$ W_ {j} \: = \: i_ {p}, \: \: \: ở đâu \: j \: \ in \ lbrace1, ...., k \ rbrace \: và \: p \: \ trong \ lbrace1, ...., n \ rbrace $$

Từng cụm C_j được liên kết với nguyên mẫu w_j.

Step 2 - Lặp lại bước 3-5 cho đến khi E không còn giảm nữa, hoặc thành viên của cụm không còn thay đổi.

Step 3 - Đối với mỗi vector đầu vào i_p Ở đâu p ∈ {1,…,n}, đặt i_p trong cụm C_j* với nguyên mẫu gần nhất w_j* có mối quan hệ sau

$$ | i_ {p} \: - \: w_ {j *} | \: \ leq \: | i_ {p} \: - \: w_ {j} |, \: j \: \ in \ lbrace1, ...., k \ rbrace $$

Step 4 - Đối với từng cụm C_j, Ở đâu j ∈ { 1,…,k}, cập nhật nguyên mẫu w_j trở thành trung tâm của tất cả các mẫu hiện tại C_j , vậy nên

$$ w_ {j} \: = \: \ sum_ {i_ {p} \ in C_ {j}} \ frac {i_ {p}} {| C_ {j} |} $$

Step 5 - Tính tổng sai số lượng tử hóa như sau:

$$ E \: = \: \ sum_ {j = 1} ^ k \ sum_ {i_ {p} \ in w_ {j}} | i_ {p} \: - \: w_ {j} | ^ 2 $$

Neocognitron

Nó là một mạng chuyển tiếp nhiều lớp, được phát triển bởi Fukushima vào năm 1980. Mô hình này dựa trên việc học có giám sát và được sử dụng để nhận dạng mẫu trực quan, chủ yếu là các ký tự viết tay. Về cơ bản nó là một phần mở rộng của mạng Cognitron, cũng được phát triển bởi Fukushima vào năm 1975.

Ngành kiến trúc

Nó là một mạng phân cấp, bao gồm nhiều lớp và có một kiểu kết nối cục bộ trong các lớp đó.

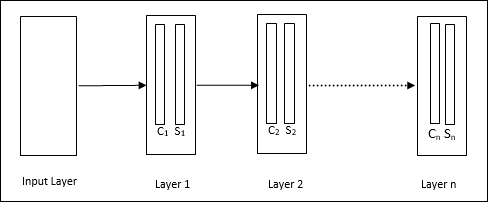
Như chúng ta đã thấy trong sơ đồ trên, neocognitron được chia thành các lớp kết nối khác nhau và mỗi lớp có hai ô. Giải thích về các ô này như sau:

S-Cell - Nó được gọi là một ô đơn giản, được huấn luyện để phản ứng với một mẫu hoặc một nhóm mẫu cụ thể.

C-Cell- Nó được gọi là ô phức hợp, kết hợp đầu ra từ ô S và đồng thời làm giảm số lượng đơn vị trong mỗi mảng. Theo một nghĩa khác, ô C thay thế kết quả của ô S.

Thuật toán đào tạo

Việc đào tạo neocognitron được phát hiện từng lớp một. Các trọng lượng từ lớp đầu vào đến lớp đầu tiên được đào tạo và đóng băng. Sau đó, các trọng lượng từ lớp đầu tiên đến lớp thứ hai được huấn luyện, v.v. Các tính toán nội bộ giữa S-cell và Ccell phụ thuộc vào trọng lượng đến từ các lớp trước đó. Do đó, chúng ta có thể nói rằng thuật toán huấn luyện phụ thuộc vào các phép tính trên ô S và ô C.