Học tập có giám sát

Như tên cho thấy, supervised learningdiễn ra dưới sự giám sát của một giáo viên. Quá trình học tập này là phụ thuộc. Trong quá trình đào tạo ANN theo phương pháp học có giám sát, vectơ đầu vào được trình bày cho mạng, vectơ này sẽ tạo ra một vectơ đầu ra. Vectơ đầu ra này được so sánh với vectơ đầu ra mong muốn / mục tiêu. Tín hiệu lỗi được tạo ra nếu có sự khác biệt giữa đầu ra thực tế và vector đầu ra mong muốn / đích. Trên cơ sở của tín hiệu lỗi này, trọng số sẽ được điều chỉnh cho đến khi đầu ra thực tế khớp với đầu ra mong muốn.

Perceptron

Được phát triển bởi Frank Rosenblatt bằng cách sử dụng mô hình McCulloch và Pitts, perceptron là đơn vị hoạt động cơ bản của mạng nơ-ron nhân tạo. Nó sử dụng quy tắc học có giám sát và có thể phân loại dữ liệu thành hai lớp.

Đặc điểm hoạt động của tế bào cảm thụ: Nó bao gồm một tế bào thần kinh duy nhất với số lượng đầu vào tùy ý cùng với trọng lượng có thể điều chỉnh, nhưng đầu ra của tế bào thần kinh là 1 hoặc 0 tùy thuộc vào ngưỡng. Nó cũng bao gồm một sai lệch có trọng số luôn là 1. Hình dưới đây cho ta biểu diễn giản đồ của perceptron.

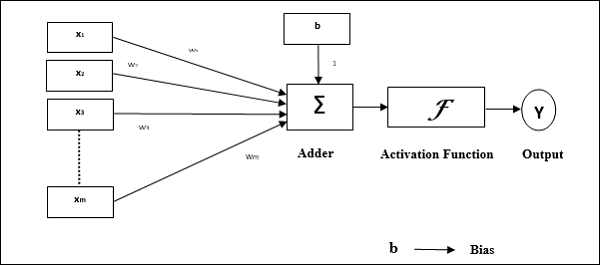
Do đó, Perceptron có ba phần tử cơ bản sau:

• Links - Nó sẽ có một tập hợp các liên kết kết nối, mang trọng số bao gồm thiên vị luôn có trọng số 1.

• Adder - Nó thêm đầu vào sau khi chúng được nhân với trọng số tương ứng của chúng.

• Activation function- Nó giới hạn đầu ra của nơron. Chức năng kích hoạt cơ bản nhất là chức năng bước Heaviside có hai đầu ra có thể. Hàm này trả về 1, nếu đầu vào là dương và 0 đối với bất kỳ đầu vào âm nào.

Thuật toán đào tạo

Mạng Perceptron có thể được huấn luyện cho đơn vị đầu ra duy nhất cũng như nhiều đơn vị đầu ra.

Thuật toán đào tạo cho đơn vị đầu ra đơn

Step 1 - Khởi tạo phần sau để bắt đầu đào tạo -

• Weights
• Bias
• Tỷ lệ học tập $ \ alpha $

Để dễ tính toán và đơn giản, trọng số và độ lệch phải được đặt bằng 0 và tốc độ học tập phải được đặt bằng 1.

Step 2 - Tiếp tục bước 3-8 khi điều kiện dừng không đúng.

Step 3 - Tiếp tục bước 4-6 cho mọi vector đào tạo x.

Step 4 - Kích hoạt từng đơn vị đầu vào như sau -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: to \: n) $$

Step 5 - Bây giờ lấy đầu vào ròng với quan hệ sau:

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limit_ {i} ^ n x_ {i}. \: w_ {i} $$

Đây ‘b’ là thiên vị và ‘n’ là tổng số nơ-ron đầu vào.

Step 6 - Áp dụng chức năng kích hoạt sau để có được kết quả cuối cùng.

$$ f (y_ {in}) \: = \: \ begin {case} 1 & if \: y_ {in} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {in} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {in} \: <\: - \ theta \ end {case} $$

Step 7 - Điều chỉnh trọng lượng và độ chệch như sau -

Case 1 - nếu y ≠ t sau đó,

$$ w_ {i} (mới) \: = \: w_ {i} (cũ) \: + \: \ alpha \: tx_ {i} $$

$$ b (mới) \: = \: b (cũ) \: + \: \ alpha t $$

Case 2 - nếu y = t sau đó,

$$ w_ {i} (mới) \: = \: w_ {i} (cũ) $$

$$ b (mới) \: = \: b (cũ) $$

Đây ‘y’ là sản lượng thực tế và ‘t’ là đầu ra mong muốn / mục tiêu.

Step 8 - Kiểm tra điều kiện dừng, sẽ xảy ra khi không có sự thay đổi về trọng lượng.

Thuật toán đào tạo cho nhiều đơn vị đầu ra

Sơ đồ sau là kiến ​​trúc của perceptron cho nhiều lớp đầu ra.

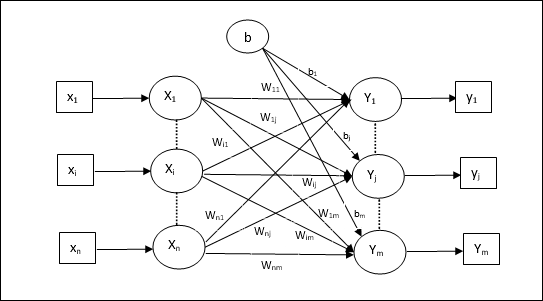
Step 1 - Khởi tạo phần sau để bắt đầu đào tạo -

• Weights
• Bias
• Tỷ lệ học tập $ \ alpha $

Để dễ tính toán và đơn giản, trọng số và độ lệch phải được đặt bằng 0 và tốc độ học tập phải được đặt bằng 1.

Step 2 - Tiếp tục bước 3-8 khi điều kiện dừng không đúng.

Step 3 - Tiếp tục bước 4-6 cho mọi vector đào tạo x.

Step 4 - Kích hoạt từng đơn vị đầu vào như sau -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: to \: n) $$

Step 5 - Lấy đầu vào ròng với mối quan hệ sau:

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limit_ {i} ^ n x_ {i} \: w_ {ij} $$

Đây ‘b’ là thiên vị và ‘n’ là tổng số nơ-ron đầu vào.

Step 6 - Áp dụng chức năng kích hoạt sau để có được đầu ra cuối cùng cho mỗi đơn vị đầu ra j = 1 to m -

$$ f (y_ {in}) \: = \: \ begin {case} 1 & if \: y_ {secure} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {secure} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {secure} \: <\: - \ theta \ end {case} $$

Step 7 - Điều chỉnh trọng lượng và thiên vị cho x = 1 to n và j = 1 to m như sau -

Case 1 - nếu y_j ≠ t_j sau đó,

$$ w_ {ij} (mới) \: = \: w_ {ij} (cũ) \: + \: \ alpha \: t_ {j} x_ {i} $$

$$ b_ {j} (mới) \: = \: b_ {j} (cũ) \: + \: \ alpha t_ {j} $$

Case 2 - nếu y_j = t_j sau đó,

$$ w_ {ij} (mới) \: = \: w_ {ij} (cũ) $$

$$ b_ {j} (mới) \: = \: b_ {j} (cũ) $$

Đây ‘y’ là sản lượng thực tế và ‘t’ là đầu ra mong muốn / mục tiêu.

Step 8 - Kiểm tra điều kiện dừng, sẽ xảy ra khi không có sự thay đổi về trọng lượng.

Neuron tuyến tính thích ứng (Adaline)

Adaline là viết tắt của Adaptive Linear Neuron, là một mạng có một đơn vị tuyến tính duy nhất. Nó được phát triển bởi Widrow và Hoff vào năm 1960. Một số điểm quan trọng về Adaline như sau:

• Nó sử dụng chức năng kích hoạt lưỡng cực.

• Nó sử dụng quy tắc delta để đào tạo nhằm giảm thiểu Sai số trung bình bình phương (MSE) giữa đầu ra thực tế và đầu ra mong muốn / mục tiêu.

• Có thể điều chỉnh trọng lượng và độ lệch.

Ngành kiến ​​trúc

Cấu trúc cơ bản của Adaline tương tự như perceptron có thêm một vòng phản hồi với sự trợ giúp của đầu ra thực tế được so sánh với đầu ra mong muốn / mục tiêu. Sau khi so sánh trên cơ sở thuật toán huấn luyện, trọng số và độ lệch sẽ được cập nhật.

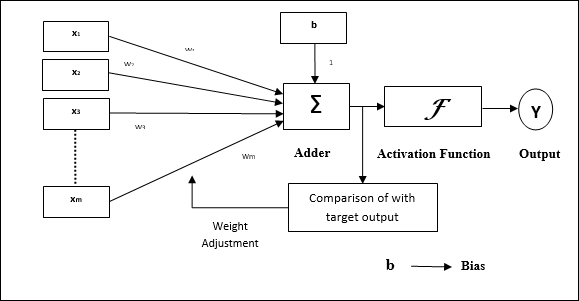
Thuật toán đào tạo

Step 1 - Khởi tạo phần sau để bắt đầu đào tạo -

• Weights
• Bias
• Tỷ lệ học tập $ \ alpha $

Để dễ tính toán và đơn giản, trọng số và độ lệch phải được đặt bằng 0 và tốc độ học tập phải được đặt bằng 1.

Step 2 - Tiếp tục bước 3-8 khi điều kiện dừng không đúng.

Step 3 - Tiếp tục bước 4-6 cho mỗi cặp huấn luyện lưỡng cực s:t.

Step 4 - Kích hoạt từng đơn vị đầu vào như sau -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: to \: n) $$

Step 5 - Lấy đầu vào ròng với mối quan hệ sau:

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limit_ {i} ^ n x_ {i} \: w_ {i} $$

Đây ‘b’ là thiên vị và ‘n’ là tổng số nơ-ron đầu vào.

Step 6 - Áp dụng chức năng kích hoạt sau để có được kết quả cuối cùng -

$$ f (y_ {in}) \: = \: \ begin {case} 1 & if \: y_ {in} \: \ geqslant \: 0 \\ - 1 & if \: y_ {in} \: < \: 0 \ end {case} $$

Step 7 - Điều chỉnh trọng lượng và độ chệch như sau -

Case 1 - nếu y ≠ t sau đó,

$$ w_ {i} (mới) \: = \: w_ {i} (cũ) \: + \: \ alpha (t \: - \: y_ {in}) x_ {i} $$

$$ b (mới) \: = \: b (cũ) \: + \: \ alpha (t \: - \: y_ {in}) $$

Case 2 - nếu y = t sau đó,

$$ w_ {i} (mới) \: = \: w_ {i} (cũ) $$

$$ b (mới) \: = \: b (cũ) $$

Đây ‘y’ là sản lượng thực tế và ‘t’ là đầu ra mong muốn / mục tiêu.

$ (t \: - \; y_ {in}) $ là lỗi tính toán.

Step 8 - Kiểm tra điều kiện dừng, sẽ xảy ra khi không có sự thay đổi trọng lượng hoặc sự thay đổi trọng lượng cao nhất xảy ra trong quá trình tập luyện nhỏ hơn dung sai quy định.

Nhiều nơron tuyến tính thích ứng (Madaline)

Madaline là viết tắt của Multiple Adaptive Linear Neuron, là một mạng bao gồm nhiều Adaline song song. Nó sẽ có một đơn vị đầu ra duy nhất. Một số điểm quan trọng về Madaline như sau:

• Nó giống như một perceptron nhiều lớp, nơi Adaline sẽ hoạt động như một đơn vị ẩn giữa đầu vào và lớp Madaline.

• Trọng số và độ lệch giữa các lớp đầu vào và Adaline, như chúng ta thấy trong kiến ​​trúc Adaline, có thể điều chỉnh được.

• Các lớp Adaline và Madaline có trọng lượng cố định và độ lệch là 1.

• Việc đào tạo có thể được thực hiện với sự trợ giúp của quy tắc Delta.

Ngành kiến ​​trúc

Kiến trúc của Madaline bao gồm “n” tế bào thần kinh của lớp đầu vào, “m”tế bào thần kinh của lớp Adaline, và 1 tế bào thần kinh của lớp Madaline. Lớp Adaline có thể được coi là lớp ẩn vì nó nằm giữa lớp đầu vào và lớp đầu ra, tức là lớp Madaline.

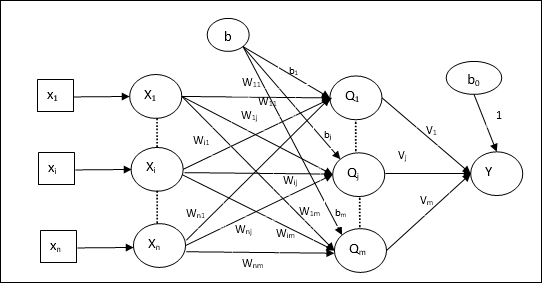
Thuật toán đào tạo

Bây giờ chúng ta biết rằng chỉ có trọng số và độ lệch giữa đầu vào và lớp Adaline mới được điều chỉnh, còn trọng số và độ lệch giữa Adaline và lớp Madaline được cố định.

Step 1 - Khởi tạo phần sau để bắt đầu đào tạo -

• Weights
• Bias
• Tỷ lệ học tập $ \ alpha $

Để dễ tính toán và đơn giản, trọng số và độ lệch phải được đặt bằng 0 và tốc độ học tập phải được đặt bằng 1.

Step 2 - Tiếp tục bước 3-8 khi điều kiện dừng không đúng.

Step 3 - Tiếp tục bước 4-6 cho mỗi cặp huấn luyện lưỡng cực s:t.

Step 4 - Kích hoạt từng đơn vị đầu vào như sau -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: to \: n) $$

Step 5 - Lấy đầu vào ròng tại mỗi lớp ẩn, tức là lớp Adaline với mối quan hệ sau:

$$ Q_ {secure} \: = \: b_ {j} \: + \: \ displaystyle \ sum \ limit_ {i} ^ n x_ {i} \: w_ {ij} \: \: \: j \: = \: 1 \: tới \: m $$

Đây ‘b’ là thiên vị và ‘n’ là tổng số nơ-ron đầu vào.

Step 6 - Áp dụng chức năng kích hoạt sau để có được kết quả cuối cùng ở lớp Adaline và lớp Madaline -

$$ f (x) \: = \: \ begin {case} 1 & if \: x \: \ geqslant \: 0 \\ - 1 & if \: x \: <\: 0 \ end {case} $ $

Đầu ra ở đơn vị ẩn (Adaline)

$$ Q_ {j} \: = \: f (Q_ {cast}) $$

Đầu ra cuối cùng của mạng

$$ y \: = \: f (y_ {in}) $$

i.e. $ \: \: y_ {cast} \: = \: b_ {0} \: + \: \ sum_ {j = 1} ^ m \: Q_ {j} \: v_ {j} $

Step 7 - Tính sai số và điều chỉnh trọng số như sau -

Case 1 - nếu y ≠ t và t = 1 sau đó,

$$ w_ {ij} (mới) \: = \: w_ {ij} (cũ) \: + \: \ alpha (1 \: - \: Q_ {inv}) x_ {i} $$

$$ b_ {j} (mới) \: = \: b_ {j} (cũ) \: + \: \ alpha (1 \: - \: Q_ {tiêm}) $$

Trong trường hợp này, trọng số sẽ được cập nhật trên Q_j trong đó đầu vào ròng gần bằng 0 vì t = 1.

Case 2 - nếu y ≠ t và t = -1 sau đó,

$$ w_ {ik} (mới) \: = \: w_ {ik} (cũ) \: + \: \ alpha (-1 \: - \: Q_ {ink}) x_ {i} $$

$$ b_ {k} (mới) \: = \: b_ {k} (cũ) \: + \: \ alpha (-1 \: - \: Q_ {ink}) $$

Trong trường hợp này, trọng số sẽ được cập nhật trên Q_k trong đó đầu vào ròng là dương vì t = -1.

Đây ‘y’ là sản lượng thực tế và ‘t’ là đầu ra mong muốn / mục tiêu.

Case 3 - nếu y = t sau đó

Sẽ không có thay đổi về trọng lượng.

Step 8 - Kiểm tra điều kiện dừng, sẽ xảy ra khi không có sự thay đổi trọng lượng hoặc sự thay đổi trọng lượng cao nhất xảy ra trong quá trình tập luyện nhỏ hơn dung sai quy định.

Mạng thần kinh lan truyền trở lại

Mạng nơ ron truyền ngược (BPN) là một mạng nơ ron đa lớp bao gồm lớp đầu vào, ít nhất một lớp ẩn và lớp đầu ra. Như tên gọi của nó cho thấy, truyền ngược sẽ diễn ra trong mạng này. Lỗi được tính toán ở lớp đầu ra, bằng cách so sánh đầu ra mục tiêu và đầu ra thực tế, sẽ được truyền ngược trở lại lớp đầu vào.

Ngành kiến ​​trúc

Như thể hiện trong sơ đồ, kiến ​​trúc của BPN có ba lớp liên kết với nhau có trọng số trên chúng. Lớp ẩn cũng như lớp đầu ra cũng có độ lệch, có trọng số luôn là 1 trên chúng. Như đã thấy rõ từ sơ đồ, hoạt động của BPN gồm hai giai đoạn. Một pha gửi tín hiệu từ lớp đầu vào đến lớp đầu ra, và pha kia truyền lại lỗi từ lớp đầu ra đến lớp đầu vào.

Thuật toán đào tạo

Để đào tạo, BPN sẽ sử dụng chức năng kích hoạt sigmoid nhị phân. Việc đào tạo BPN sẽ có ba giai đoạn sau.

• Phase 1 - Giai đoạn chuyển tiếp nguồn cấp dữ liệu

• Phase 2 - Lùi lại lỗi lan truyền

• Phase 3 - Cập nhật trọng lượng

Tất cả các bước này sẽ được kết luận trong thuật toán như sau

Step 1 - Khởi tạo phần sau để bắt đầu đào tạo -

• Weights
• Tỷ lệ học tập $ \ alpha $

Để dễ dàng tính toán và đơn giản, hãy lấy một số giá trị ngẫu nhiên nhỏ.

Step 2 - Tiếp tục bước 3-11 khi điều kiện dừng không đúng.

Step 3 - Tiếp tục bước 4-10 cho mỗi cặp huấn luyện.

Giai đoạn 1

Step 4 - Mỗi đơn vị đầu vào nhận tín hiệu đầu vào x_i và gửi nó đến đơn vị ẩn cho tất cả i = 1 to n

Step 5 - Tính toán đầu vào ròng tại đơn vị ẩn theo quan hệ sau:

$$ Q_ {secure} \: = \: b_ {0j} \: + \: \ sum_ {i = 1} ^ n x_ {i} v_ {ij} \: \: \: \: \: j \: = \ : 1 \: đến \: p $$

Đây b_0j là thiên vị về đơn vị ẩn, v_ij trọng lượng trên j đơn vị của lớp ẩn đến từ i đơn vị của lớp đầu vào.

Bây giờ hãy tính toán sản lượng ròng bằng cách áp dụng hàm kích hoạt sau

$$ Q_ {j} \: = \: f (Q_ {cast}) $$

Gửi các tín hiệu đầu ra này của các đơn vị lớp ẩn tới các đơn vị lớp đầu ra.

Step 6 - Tính toán đầu vào ròng tại đơn vị lớp đầu ra theo quan hệ sau:

$$ y_ {ink} \: = \: b_ {0k} \: + \: \ sum_ {j = 1} ^ p \: Q_ {j} \: w_ {jk} \: \: k \: = \ : 1 \: đến \: m $$

Đây b_0k ⁡Là sai lệch về đơn vị đầu ra, w_jk trọng lượng trên k đơn vị của lớp đầu ra đến từ j đơn vị của lớp ẩn.

Tính toán sản lượng ròng bằng cách áp dụng chức năng kích hoạt sau

$$ y_ {k} \: = \: f (y_ {ink}) $$

Giai đoạn 2

Step 7 - Tính toán thời hạn sửa lỗi, tương ứng với mẫu đích nhận được ở mỗi đơn vị đầu ra, như sau:

$$ \ delta_ {k} \: = \ :( t_ {k} \: - \: y_ {k}) f ^ {'} (y_ {ink}) $$

Trên cơ sở này, cập nhật trọng số và độ chệch như sau:

$$ \ Delta v_ {jk} \: = \: \ alpha \ delta_ {k} \: Q_ {ij} $$

$$ \ Delta b_ {0k} \: = \: \ alpha \ delta_ {k} $$

Sau đó, gửi $ \ delta_ {k} $ trở lại lớp ẩn.

Step 8 - Bây giờ mỗi đơn vị ẩn sẽ là tổng các đầu vào delta của nó từ các đơn vị đầu ra.

$$ \ delta_ {secure} \: = \: \ displaystyle \ sum \ limit_ {k = 1} ^ m \ delta_ {k} \: w_ {jk} $$

Thuật ngữ lỗi có thể được tính như sau:

$$ \ delta_ {j} \: = \: \ delta_ {casting} f ^ {'} (Q_ {inv}) $$

Trên cơ sở này, cập nhật trọng số và độ chệch như sau:

$$ \ Delta w_ {ij} \: = \: \ alpha \ delta_ {j} x_ {i} $$

$$ \ Delta b_ {0j} \: = \: \ alpha \ delta_ {j} $$

Giai đoạn 3

Step 9 - Mỗi đơn vị đầu ra (y_kk = 1 to m) cập nhật trọng lượng và độ lệch như sau:

$$ v_ {jk} (mới) \: = \: v_ {jk} (cũ) \: + \: \ Delta v_ {jk} $$

$$ b_ {0k} (mới) \: = \: b_ {0k} (cũ) \: + \: \ Delta b_ {0k} $$

Step 10 - Mỗi đơn vị đầu ra (z_jj = 1 to p) cập nhật trọng lượng và độ lệch như sau:

$$ w_ {ij} (mới) \: = \: w_ {ij} (cũ) \: + \: \ Delta w_ {ij} $$

$$ b_ {0j} (mới) \: = \: b_ {0j} (cũ) \: + \: \ Delta b_ {0j} $$

Step 11 - Kiểm tra điều kiện dừng, có thể là số kỷ nguyên đã đạt được hoặc đầu ra mục tiêu khớp với đầu ra thực tế.

Quy tắc học tập Delta tổng quát

Quy tắc Delta chỉ hoạt động cho lớp đầu ra. Mặt khác, quy tắc đồng bằng tổng quát, còn được gọi làback-propagation là một cách tạo ra các giá trị mong muốn của lớp ẩn.

Công thức toán học

Đối với chức năng kích hoạt $ y_ {k} \: = \: f (y_ {ink}) $, dẫn xuất của đầu vào ròng trên lớp Ẩn cũng như trên lớp đầu ra có thể được cung cấp bởi

$$ y_ {ink} \: = \: \ displaystyle \ sum \ limit_i \: z_ {i} w_ {jk} $$

Và $ \: \: y_ {inv} \: = \: \ sum_i x_ {i} v_ {ij} $

Bây giờ, lỗi phải được giảm thiểu là

$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ limit_ {k} \: [t_ {k} \: - \: y_ {k}] ^ 2 $$

Bằng cách sử dụng quy tắc chuỗi, chúng tôi có

$$ \ frac {\ một phần E} {\ một phần w_ {jk}} \: = \: \ frac {\ một phần} {\ một phần w_ {jk}} (\ frac {1} {2} \ displaystyle \ sum \ giới hạn_ {k} \: [t_ {k} \: - \: y_ {k}] ^ 2) $$

$$ = \: \ frac {\ part} {\ một phần w_ {jk}} \ lgroup \ frac {1} {2} [t_ {k} \: - \: t (y_ {ink})] ^ 2 \ rgroup $$

$$ = \: - [t_ {k} \: - \: y_ {k}] \ frac {\ part} {\ một phần w_ {jk}} f (y_ {ink}) $$

$$ = \: - [t_ {k} \: - \: y_ {k}] f (y_ {ink}) \ frac {\ part} {\ part w_ {jk}} (y_ {ink}) $$

$$ = \: - [t_ {k} \: - \: y_ {k}] f ^ {'} (y_ {ink}) z_ {j} $$

Bây giờ chúng ta hãy nói $ \ delta_ {k} \: = \: - [t_ {k} \: - \: y_ {k}] f ^ {'} (y_ {ink}) $

Trọng lượng của các kết nối với thiết bị ẩn z_j có thể được đưa ra bởi -

$$ \ frac {\ một phần E} {\ một phần v_ {ij}} \: = \: - \ displaystyle \ sum \ limit_ {k} \ delta_ {k} \ frac {\ một phần} {\ một phần v_ {ij} } \ :( y_ {ink}) $$

Đặt giá trị $ y_ {ink} $ chúng ta sẽ nhận được những điều sau

$$ \ delta_ {j} \: = \: - \ displaystyle \ sum \ limit_ {k} \ delta_ {k} w_ {jk} f ^ {'} (z_ {secure}) $$

Việc cập nhật trọng lượng có thể được thực hiện như sau:

Đối với đơn vị đầu ra -

$$ \ Delta w_ {jk} \: = \: - \ alpha \ frac {\ một phần E} {\ một phần w_ {jk}} $$

$$ = \: \ alpha \: \ delta_ {k} \: z_ {j} $$

Đối với đơn vị ẩn -

$$ \ Delta v_ {ij} \: = \: - \ alpha \ frac {\ một phần E} {\ một phần v_ {ij}} $$

$$ = \: \ alpha \: \ delta_ {j} \: x_ {i} $$