Tối ưu hóa Sử dụng Mạng Hopfield
Tối ưu hóa là một hành động làm cho một cái gì đó như thiết kế, tình huống, tài nguyên và hệ thống trở nên hiệu quả nhất có thể. Sử dụng sự tương đồng giữa hàm chi phí và hàm năng lượng, chúng ta có thể sử dụng các nơ-ron có tính liên kết cao để giải quyết các vấn đề tối ưu hóa. Một loại mạng nơ-ron như vậy là mạng Hopfield, bao gồm một lớp đơn chứa một hoặc nhiều nơ-ron lặp lại được kết nối đầy đủ. Điều này có thể được sử dụng để tối ưu hóa.
Những điểm cần nhớ khi sử dụng mạng Hopfield để tối ưu hóa -
Hàm năng lượng phải nhỏ nhất của mạng.
Nó sẽ tìm ra giải pháp thỏa đáng hơn là chọn một trong số các mẫu được lưu trữ.
Chất lượng của giải pháp được tìm thấy bởi mạng Hopfield phụ thuộc đáng kể vào trạng thái ban đầu của mạng.
Vấn đề nhân viên bán hàng đi du lịch
Tìm tuyến đường ngắn nhất mà nhân viên bán hàng đi là một trong những bài toán tính toán, có thể được tối ưu hóa bằng cách sử dụng mạng nơ-ron Hopfield.
Khái niệm cơ bản về TSP
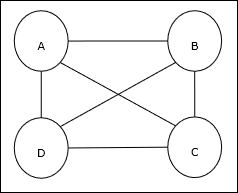
Bài toán người bán hàng đi du lịch (TSP) là một bài toán tối ưu hóa cổ điển trong đó người bán hàng phải đi du lịch ncác thành phố được kết nối với nhau, giữ cho chi phí cũng như khoảng cách di chuyển ở mức tối thiểu. Ví dụ: nhân viên bán hàng phải đi du lịch một nhóm 4 thành phố A, B, C, D và mục tiêu là tìm chuyến tham quan vòng tròn ngắn nhất, ABC – D, để giảm thiểu chi phí, cũng bao gồm chi phí đi từ thành phố D cuối cùng đến thành phố A đầu tiên.
Biểu diễn ma trận
Trên thực tế, mỗi chuyến tham quan TSP n-city có thể được thể hiện như n × n ma trận có ith hàng mô tả ithvị trí của thành phố. Ma trận này,M, đối với 4 thành phố A, B, C, D có thể được biểu thị như sau:
$$ M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 & 0 & 1 \ end {bmatrix} $$
Giải pháp của Hopfield Network
Trong khi xem xét giải pháp của mạng TSP bởi Hopfield này, mọi nút trong mạng tương ứng với một phần tử trong ma trận.
Tính toán hàm năng lượng
Để trở thành giải pháp tối ưu hóa, hàm năng lượng phải ở mức tối thiểu. Trên cơ sở các ràng buộc sau, chúng ta có thể tính hàm năng lượng như sau:
Ràng buộc-I
Ràng buộc đầu tiên, trên cơ sở đó chúng ta sẽ tính toán hàm năng lượng, là một phần tử phải bằng 1 trong mỗi hàng của ma trận M và các phần tử khác trong mỗi hàng phải bằng 0bởi vì mỗi thành phố chỉ có thể xảy ra ở một vị trí trong chuyến tham quan TSP. Ràng buộc này có thể được viết về mặt toán học như sau:
$$ \ displaystyle \ sum \ limit_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: for \: x \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Bây giờ hàm năng lượng được tối thiểu hóa, dựa trên ràng buộc ở trên, sẽ chứa một số hạng tỷ lệ với -
$$ \ displaystyle \ sum \ limit_ {x = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {j = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$
Constraint-II
Như chúng ta đã biết, trong TSP, một thành phố có thể xuất hiện ở bất kỳ vị trí nào trong chuyến tham quan do đó trong mỗi cột ma trận M, một phần tử phải bằng 1 và các phần tử khác phải bằng 0. Ràng buộc này có thể được viết về mặt toán học như sau:
$$ \ displaystyle \ sum \ limit_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: for \: j \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Bây giờ hàm năng lượng được tối thiểu hóa, dựa trên ràng buộc ở trên, sẽ chứa một số hạng tỷ lệ với -
$$ \ displaystyle \ sum \ limit_ {j = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {x = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$
Tính toán hàm chi phí
Giả sử một ma trận vuông của (n × n) đóng góp bởi C biểu thị ma trận chi phí của TSP cho n thành phố nơi n > 0. Sau đây là một số tham số trong khi tính toán hàm chi phí:
Cx, y - Yếu tố của ma trận chi phí biểu thị chi phí đi từ thành phố x đến y.
Sự liền kề của các phần tử của A và B có thể được thể hiện bằng quan hệ sau:
$$ M_ {x, i} \: = \: 1 \: \: và \: \: M_ {y, i \ pm 1} \: = \: 1 $$
Như chúng ta đã biết, trong Ma trận giá trị đầu ra của mỗi nút có thể là 0 hoặc 1, do đó đối với mọi cặp thành phố A, B, chúng ta có thể thêm các số hạng sau vào hàm năng lượng:
$$ \ displaystyle \ sum \ limit_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$
Trên cơ sở của hàm chi phí và giá trị ràng buộc ở trên, hàm năng lượng cuối cùng E có thể được đưa ra như sau:
$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ limit_ {i = 1} ^ n \ displaystyle \ sum \ limit_ {x} \ displaystyle \ sum \ limit_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$
$$ \: \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ limit_ {x} \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {i} M_ {x, i} \ end {array} \ right) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limit_ {i} \ left (\ begin {array} {c} 1 \: - \ : \ displaystyle \ sum \ limit_ {x} M_ {x, i} \ end {array} \ right) ^ 2 \ end {bmatrix} $$
Đây, γ1 và γ2 là hai hằng số cân.