Cấu trúc dữ liệu và thuật toán - Cây AVL

Điều gì sẽ xảy ra nếu đầu vào cho cây tìm kiếm nhị phân theo cách được sắp xếp (tăng dần hoặc giảm dần)? Sau đó nó sẽ giống như thế này -

Quan sát thấy rằng hiệu suất trong trường hợp xấu nhất của BST gần nhất với các thuật toán tìm kiếm tuyến tính, đó là Ο (n). Trong dữ liệu thời gian thực, chúng tôi không thể dự đoán mẫu dữ liệu và tần số của chúng. Vì vậy, một nhu cầu phát sinh để cân bằng các BST hiện có.

Được đặt tên theo nhà phát minh của họ Adelson, Velski & Landis, AVL treeslà cây tìm kiếm nhị phân cân bằng chiều cao. Cây AVL kiểm tra chiều cao của cây con bên trái và bên phải và đảm bảo rằng sự khác biệt không quá 1. Sự khác biệt này được gọi làBalance Factor.

Ở đây ta thấy rằng cây đầu tiên cân bằng và hai cây tiếp theo không cân bằng -

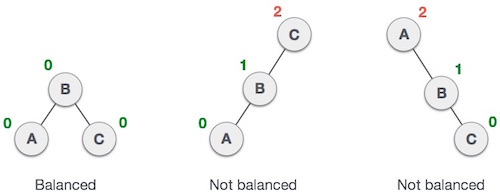
Trong cây thứ hai, cây con bên trái của C có chiều cao 2 và cây con bên phải có chiều cao 0, do đó hiệu số là 2. Trong cây thứ ba, cây con bên phải của Acó chiều cao 2 và bên trái bị thiếu, vì vậy nó là 0, và sự khác biệt là 2 một lần nữa. Cây AVL cho phép chênh lệch (hệ số cân bằng) chỉ là 1.

BalanceFactor = height(left-sutree) − height(right-sutree)

Nếu sự khác biệt về chiều cao của các cây phụ bên trái và bên phải lớn hơn 1 thì cây được cân bằng bằng một số kỹ thuật luân canh.

Vòng quay AVL

Để tự cân bằng, cây AVL có thể thực hiện bốn kiểu xoay sau:

Xoay trái
Xoay phải
Xoay trái-phải
Xoay phải-trái

Hai phép quay đầu tiên là phép quay đơn và hai phép quay tiếp theo là phép quay kép. Để có một cây không cân đối, ít nhất chúng ta cần một cây có chiều cao 2. Với loại cây đơn giản này, chúng ta hãy tìm hiểu từng cây một.

Xoay trái

Nếu một cây trở nên không cân bằng, khi một nút được chèn vào cây con bên phải của cây con bên phải, thì chúng ta thực hiện một phép quay sang trái duy nhất -

Trong ví dụ của chúng tôi, nút Ađã trở nên không cân bằng khi một nút được chèn vào cây con bên phải của cây con bên phải của A. Chúng tôi thực hiện xoay trái bằng cáchA cây con bên trái của B.

Xoay phải

Cây AVL có thể trở nên không cân bằng, nếu một nút được chèn vào cây con bên trái của cây con bên trái. Khi đó cây cần phải luân chuyển.

Như được mô tả, nút không cân bằng trở thành nút con bên phải của nút con bên trái của nó bằng cách thực hiện xoay phải.

Xoay trái-phải

Phép quay kép là phiên bản hơi phức tạp của các phiên bản xoay đã được giải thích. Để hiểu rõ hơn về chúng, chúng ta nên lưu ý từng hành động được thực hiện trong khi xoay. Đầu tiên chúng ta hãy kiểm tra cách thực hiện xoay Trái-Phải. Xoay trái-phải là sự kết hợp của xoay trái sau đó xoay phải.

Tiểu bang	Hoạt động
	Một nút đã được chèn vào cây con bên phải của cây con bên trái. Điều này làm choCmột nút không cân bằng. Các kịch bản này khiến cây AVL thực hiện xoay trái-phải.
	Đầu tiên chúng tôi thực hiện xoay trái trên cây con bên trái của C. Điều này làm choA, cây con bên trái của B.
	Nút C vẫn không cân bằng, tuy nhiên bây giờ, đó là vì cây con bên trái của cây con bên trái.
	Bây giờ chúng ta sẽ xoay cây sang phải, làm cho B nút gốc mới của cây con này. C bây giờ trở thành cây con bên phải của cây con bên trái của chính nó.
	Hiện cây đã cân đối.

Xoay phải-trái

Kiểu quay kép thứ hai là Xoay phải-Trái. Nó là sự kết hợp của xoay phải sau đó xoay trái.

Tiểu bang	Hoạt động
	Một nút đã được chèn vào cây con bên trái của cây con bên phải. Điều này làm choA, một nút không cân bằng với hệ số cân bằng 2.
	Đầu tiên, chúng tôi thực hiện xoay bên phải cùng C nút, làm C cây con bên phải của cây con bên trái của chính nó B. Hiện nay,B trở thành cây con bên phải của A.
	Nút A vẫn không cân bằng vì cây con bên phải của cây con bên phải của nó và yêu cầu quay trái.
	Xoay trái được thực hiện bằng cách B nút gốc mới của cây con. A trở thành cây con bên trái của cây con bên phải của nó B.
	Hiện cây đã cân đối.