Cấu trúc dữ liệu & thuật toán - Hướng dẫn nhanh

Cấu trúc dữ liệu là một cách có hệ thống để tổ chức dữ liệu nhằm sử dụng nó một cách hiệu quả. Các thuật ngữ sau đây là các thuật ngữ nền tảng của cấu trúc dữ liệu.

• Interface- Mỗi cấu trúc dữ liệu có một giao diện. Giao diện đại diện cho tập hợp các hoạt động mà một cấu trúc dữ liệu hỗ trợ. Một giao diện chỉ cung cấp danh sách các hoạt động được hỗ trợ, loại tham số mà chúng có thể chấp nhận và loại trả về của các hoạt động này.

• Implementation- Việc thực hiện cung cấp sự biểu diễn bên trong của một cấu trúc dữ liệu. Việc triển khai cũng cung cấp định nghĩa của các thuật toán được sử dụng trong các hoạt động của cấu trúc dữ liệu.

Đặc điểm của cấu trúc dữ liệu

• Correctness - Việc triển khai cấu trúc dữ liệu nên thực hiện đúng giao diện của nó.

• Time Complexity - Thời gian chạy hoặc thời gian thực hiện các thao tác của cấu trúc dữ liệu phải càng nhỏ càng tốt.

• Space Complexity - Việc sử dụng bộ nhớ của một hoạt động cấu trúc dữ liệu nên càng ít càng tốt.

Cần cấu trúc dữ liệu

Khi các ứng dụng ngày càng phức tạp và dữ liệu phong phú, có ba vấn đề phổ biến mà các ứng dụng phải đối mặt ngay bây giờ.

• Data Search- Xem xét số lượng tồn kho 1 triệu (10 ⁶ ) mặt hàng của một cửa hàng. Nếu ứng dụng là để tìm kiếm một mục, nó phải tìm kiếm một mục trong 1 triệu (10 ⁶ ) mục mỗi khi làm chậm tìm kiếm. Khi dữ liệu phát triển, tìm kiếm sẽ trở nên chậm hơn.

• Processor speed - Tốc độ bộ xử lý mặc dù rất cao nhưng sẽ bị giới hạn nếu dữ liệu tăng lên đến hàng tỷ bản ghi.

• Multiple requests - Vì hàng nghìn người dùng có thể tìm kiếm dữ liệu đồng thời trên một máy chủ web, thậm chí máy chủ nhanh bị lỗi khi đang tìm kiếm dữ liệu.

Để giải quyết các vấn đề nêu trên, cấu trúc dữ liệu ra đời để giải cứu. Dữ liệu có thể được tổ chức theo cấu trúc dữ liệu theo cách mà tất cả các mục có thể không được yêu cầu tìm kiếm và dữ liệu cần thiết có thể được tìm kiếm gần như ngay lập tức.

Các trường hợp thời gian thực thi

Có ba trường hợp thường được sử dụng để so sánh thời gian thực thi của các cấu trúc dữ liệu khác nhau một cách tương đối.

• Worst Case- Đây là tình huống mà một hoạt động cấu trúc dữ liệu cụ thể mất nhiều thời gian nhất có thể. Nếu thời gian trong trường hợp xấu nhất của một hoạt động là ƒ (n) thì hoạt động này sẽ không mất quá ƒ (n) thời gian trong đó ƒ (n) đại diện cho hàm của n.

• Average Case- Đây là kịch bản mô tả thời gian thực hiện trung bình của một hoạt động của một cấu trúc dữ liệu. Nếu một hoạt động cần ƒ (n) thời gian để thực hiện, thì m hoạt động sẽ mất mƒ (n) thời gian.

• Best Case- Đây là kịch bản mô tả thời gian thực hiện ít nhất có thể của một hoạt động của cấu trúc dữ liệu. Nếu một hoạt động mất ƒ (n) thời gian để thực hiện, thì hoạt động thực tế có thể mất thời gian vì số ngẫu nhiên sẽ lớn nhất là ƒ (n).

Thuật ngữ cơ bản

• Data - Dữ liệu là các giá trị hoặc tập giá trị.

• Data Item - Mục dữ liệu đề cập đến một đơn vị giá trị.

• Group Items - Các mục dữ liệu được chia thành các mục con được gọi là Mục nhóm.

• Elementary Items - Các mục dữ liệu không thể phân chia được gọi là Mục cơ bản.

• Attribute and Entity - Thực thể là thực thể chứa các thuộc tính hoặc thuộc tính nhất định, có thể được gán giá trị.

• Entity Set - Các thực thể có thuộc tính giống nhau tạo thành một tập thực thể.

• Field - Trường là một đơn vị thông tin cơ bản đại diện cho một thuộc tính của một thực thể.

• Record - Bản ghi là tập hợp các giá trị trường của một thực thể nhất định.

• File - Tệp là tập hợp các bản ghi của các thực thể trong một tập thực thể nhất định.

Dùng thử Tùy chọn trực tuyến

Bạn thực sự không cần phải thiết lập môi trường của riêng mình để bắt đầu học ngôn ngữ lập trình C. Lý do rất đơn giản, chúng tôi đã thiết lập môi trường Lập trình C trực tuyến, để bạn có thể biên dịch và thực thi tất cả các ví dụ có sẵn trực tuyến cùng một lúc khi bạn đang làm bài lý thuyết của mình. Điều này giúp bạn tin tưởng vào những gì bạn đang đọc và kiểm tra kết quả bằng các tùy chọn khác nhau. Vui lòng sửa đổi bất kỳ ví dụ nào và thực hiện trực tuyến.

Hãy thử ví dụ sau bằng cách sử dụng Try it tùy chọn có sẵn ở góc trên cùng bên phải của hộp mã mẫu -

#include <stdio.h>
int main(){
   /* My first program in C */
   printf("Hello, World! \n");
   return 0;
}

Đối với hầu hết các ví dụ được đưa ra trong hướng dẫn này, bạn sẽ tìm thấy tùy chọn Dùng thử, vì vậy hãy tận dụng nó và tận hưởng việc học của mình.

Thiết lập môi trường cục bộ

Nếu bạn vẫn sẵn sàng thiết lập môi trường của mình cho ngôn ngữ lập trình C, bạn cần có hai công cụ sau có sẵn trên máy tính của mình, (a) Trình soạn thảo văn bản và (b) Trình biên dịch C.

Trình soạn thảo văn bản

Điều này sẽ được sử dụng để nhập chương trình của bạn. Ví dụ về một số trình soạn thảo bao gồm Windows Notepad, lệnh Chỉnh sửa hệ điều hành, Tóm tắt, Epsilon, EMACS và vim hoặc vi.

Tên và phiên bản của trình soạn thảo văn bản có thể khác nhau trên các hệ điều hành khác nhau. Ví dụ: Notepad sẽ được sử dụng trên Windows và vim hoặc vi có thể được sử dụng trên Windows cũng như Linux hoặc UNIX.

Các tệp bạn tạo bằng trình chỉnh sửa của mình được gọi là tệp nguồn và chứa mã nguồn chương trình. Các tệp nguồn cho các chương trình C thường được đặt tên với phần mở rộng ".c".

Trước khi bắt đầu lập trình, hãy đảm bảo rằng bạn đã có sẵn một trình soạn thảo văn bản và bạn có đủ kinh nghiệm để viết một chương trình máy tính, lưu nó vào một tệp, biên dịch và cuối cùng là thực thi nó.

Trình biên dịch C

Mã nguồn được viết trong tệp nguồn là nguồn con người có thể đọc được cho chương trình của bạn. Nó cần được "biên dịch", chuyển thành ngôn ngữ máy để CPU của bạn có thể thực thi chương trình theo các hướng dẫn đã cho.

Trình biên dịch ngôn ngữ lập trình C này sẽ được sử dụng để biên dịch mã nguồn của bạn thành một chương trình thực thi cuối cùng. Chúng tôi cho rằng bạn có kiến ​​thức cơ bản về trình biên dịch ngôn ngữ lập trình.

Trình biên dịch miễn phí và được sử dụng thường xuyên nhất là trình biên dịch GNU C / C ++. Nếu không, bạn có thể có các trình biên dịch từ HP hoặc Solaris nếu bạn có Hệ điều hành (OS) tương ứng.

Phần sau hướng dẫn bạn cách cài đặt trình biên dịch GNU C / C ++ trên nhiều hệ điều hành khác nhau. Chúng ta đang đề cập đến C / C ++ cùng nhau vì trình biên dịch GNU GCC hoạt động cho cả ngôn ngữ lập trình C và C ++.

Cài đặt trên UNIX / Linux

Nếu bạn đang sử dụng Linux or UNIX, sau đó kiểm tra xem GCC đã được cài đặt trên hệ thống của bạn hay chưa bằng cách nhập lệnh sau từ dòng lệnh:

$ gcc -v

Nếu bạn đã cài đặt trình biên dịch GNU trên máy của mình, thì nó sẽ in một thông báo như sau:

Using built-in specs.
Target: i386-redhat-linux
Configured with: ../configure --prefix = /usr .......
Thread model: posix
gcc version 4.1.2 20080704 (Red Hat 4.1.2-46)

Nếu GCC chưa được cài đặt, thì bạn sẽ phải tự cài đặt nó bằng cách sử dụng hướng dẫn chi tiết có tại https://gcc.gnu.org/install/

Hướng dẫn này được viết dựa trên Linux và tất cả các ví dụ đã cho đã được biên dịch trên phiên bản Cent OS của hệ thống Linux.

Cài đặt trên Mac OS

Nếu bạn sử dụng Mac OS X, cách dễ nhất để lấy GCC là tải xuống môi trường phát triển Xcode từ trang web của Apple và làm theo hướng dẫn cài đặt đơn giản. Khi bạn đã thiết lập Xcode, bạn sẽ có thể sử dụng trình biên dịch GNU cho C / C ++.

Xcode hiện có sẵn tại developer.apple.com/technologies/tools/

Cài đặt trên Windows

Để cài đặt GCC trên Windows, bạn cần cài đặt MinGW. Để cài đặt MinGW, hãy truy cập trang chủ MinGW, www.mingw.org , và theo liên kết đến trang tải xuống MinGW. Tải xuống phiên bản mới nhất của chương trình cài đặt MinGW, sẽ được đặt tên là MinGW- <version> .exe.

Trong khi cài đặt MinWG, tối thiểu, bạn phải cài đặt gcc-core, gcc-g ++, binutils và thời gian chạy MinGW, nhưng bạn có thể muốn cài đặt thêm.

Thêm thư mục con bin của cài đặt MinGW của bạn vào PATH biến môi trường, để bạn có thể chỉ định các công cụ này trên dòng lệnh bằng tên đơn giản của chúng.

Khi quá trình cài đặt hoàn tất, bạn sẽ có thể chạy gcc, g ++, ar, ranlib, dlltool và một số công cụ GNU khác từ dòng lệnh Windows.

Thuật toán là một thủ tục từng bước, xác định một tập hợp các lệnh được thực hiện theo một thứ tự nhất định để có được đầu ra mong muốn. Các thuật toán thường được tạo độc lập với các ngôn ngữ cơ bản, tức là một thuật toán có thể được thực hiện bằng nhiều ngôn ngữ lập trình.

Từ quan điểm cấu trúc dữ liệu, sau đây là một số loại thuật toán quan trọng:

• Search - Thuật toán tìm kiếm một mục trong cấu trúc dữ liệu.

• Sort - Thuật toán sắp xếp các mặt hàng theo một thứ tự nhất định.

• Insert - Thuật toán chèn mục trong cấu trúc dữ liệu.

• Update - Thuật toán cập nhật một mục hiện có trong cấu trúc dữ liệu.

• Delete - Thuật toán xóa một mục hiện có khỏi cấu trúc dữ liệu.

Đặc điểm của một thuật toán

Không phải tất cả các thủ tục đều có thể được gọi là một thuật toán. Thuật toán phải có các đặc điểm sau:

• Unambiguous- Thuật toán phải rõ ràng và không mập mờ. Mỗi bước (hoặc giai đoạn) của nó và các đầu vào / đầu ra của chúng phải rõ ràng và chỉ dẫn đến một ý nghĩa.

• Input - Một thuật toán phải có 0 hoặc nhiều đầu vào được xác định rõ ràng.

• Output - Một thuật toán nên có 1 hoặc nhiều đầu ra được xác định rõ ràng và phải phù hợp với đầu ra mong muốn.

• Finiteness - Thuật toán phải kết thúc sau một số bước hữu hạn.

• Feasibility - Nên khả thi với các nguồn lực sẵn có.

• Independent - Một thuật toán nên có hướng dẫn từng bước, điều này phải độc lập với bất kỳ mã lập trình nào.

Làm thế nào để viết một thuật toán?

Không có tiêu chuẩn được xác định rõ ràng để viết thuật toán. Đúng hơn, đó là vấn đề và phụ thuộc vào tài nguyên. Các thuật toán không bao giờ được viết để hỗ trợ một mã lập trình cụ thể.

Như chúng ta biết rằng tất cả các ngôn ngữ lập trình đều có chung các cấu trúc mã cơ bản như vòng lặp (do, for, while), điều khiển luồng (if-else), v.v. Những cấu trúc chung này có thể được sử dụng để viết một thuật toán.

Chúng tôi viết các thuật toán theo cách thức từng bước, nhưng không phải lúc nào cũng vậy. Viết thuật toán là một quá trình và được thực hiện sau khi miền vấn đề được xác định rõ. Đó là, chúng ta nên biết miền vấn đề mà chúng ta đang thiết kế một giải pháp.

Thí dụ

Hãy thử học cách viết thuật toán bằng cách sử dụng một ví dụ.

Problem - Thiết kế thuật toán cộng hai số và hiển thị kết quả.

Step 1 − START
Step 2 − declare three integers a, b & c
Step 3 − define values of a & b
Step 4 − add values of a & b
Step 5 − store output of step 4 to c
Step 6 − print c
Step 7 − STOP

Các thuật toán cho người lập trình biết cách viết mã chương trình. Ngoài ra, thuật toán có thể được viết dưới dạng:

Step 1 − START ADD
Step 2 − get values of a & b
Step 3 − c ← a + b
Step 4 − display c
Step 5 − STOP

Trong thiết kế và phân tích các thuật toán, thường phương pháp thứ hai được sử dụng để mô tả một thuật toán. Nó giúp nhà phân tích dễ dàng phân tích thuật toán bỏ qua tất cả các định nghĩa không mong muốn. Anh ta có thể quan sát những thao tác nào đang được sử dụng và quy trình đang diễn ra như thế nào.

Viết step numbers, Là tùy chọn.

Chúng tôi thiết kế một thuật toán để có được một giải pháp của một vấn đề nhất định. Một vấn đề có thể được giải quyết bằng nhiều cách.

Do đó, nhiều thuật toán giải có thể được rút ra cho một vấn đề nhất định. Bước tiếp theo là phân tích các thuật toán giải pháp đề xuất đó và triển khai giải pháp phù hợp nhất.

Phân tích thuật toán

Hiệu quả của một thuật toán có thể được phân tích ở hai giai đoạn khác nhau, trước khi thực hiện và sau khi thực hiện. Chúng là những thứ sau -

• A Priori Analysis- Đây là một phân tích lý thuyết của một thuật toán. Hiệu quả của một thuật toán được đo bằng cách giả định rằng tất cả các yếu tố khác, ví dụ, tốc độ bộ xử lý, là không đổi và không ảnh hưởng đến việc triển khai.

• A Posterior Analysis- Đây là phân tích thực nghiệm của một thuật toán. Thuật toán đã chọn được thực hiện bằng ngôn ngữ lập trình. Điều này sau đó được thực hiện trên máy tính đích. Trong phân tích này, số liệu thống kê thực tế như thời gian chạy và không gian cần thiết sẽ được thu thập.

Chúng ta sẽ tìm hiểu về phân tích thuật toán tiên nghiệm . Phân tích thuật toán đề cập đến việc thực thi hoặc thời gian chạy của các hoạt động khác nhau có liên quan. Thời gian chạy của một thao tác có thể được định nghĩa là số lượng lệnh máy tính được thực hiện trên mỗi thao tác.

Độ phức tạp của thuật toán

Giả sử X là một thuật toán và n là kích thước của dữ liệu đầu vào, thời gian và không gian mà thuật toán X sử dụng là hai yếu tố chính, quyết định hiệu quả của X.

• Time Factor - Thời gian được đo bằng cách đếm số lượng các thao tác chính như so sánh trong thuật toán sắp xếp.

• Space Factor - Không gian được đo bằng cách đếm không gian bộ nhớ lớn nhất mà thuật toán yêu cầu.

Độ phức tạp của một thuật toán f(n) cung cấp thời gian chạy và / hoặc không gian lưu trữ theo yêu cầu của thuật toán về n như kích thước của dữ liệu đầu vào.

Không gian phức tạp

Độ phức tạp không gian của một thuật toán biểu thị lượng không gian bộ nhớ mà thuật toán yêu cầu trong vòng đời của nó. Không gian được yêu cầu bởi một thuật toán bằng tổng của hai thành phần sau:

• Một phần cố định là không gian cần thiết để lưu trữ dữ liệu và biến nhất định, độc lập với quy mô của vấn đề. Ví dụ, các biến và hằng số đơn giản được sử dụng, kích thước chương trình, v.v.

• Một phần biến là một không gian được yêu cầu bởi các biến, kích thước của nó phụ thuộc vào kích thước của bài toán. Ví dụ, cấp phát bộ nhớ động, không gian ngăn xếp đệ quy, v.v.

Độ phức tạp không gian S (P) của bất kỳ thuật toán P nào là S (P) = C + SP (I), trong đó C là phần cố định và S (I) là phần biến của thuật toán, phụ thuộc vào đặc tính cá thể I. Sau đây là một ví dụ đơn giản cố gắng giải thích khái niệm -

Algorithm: SUM(A, B)
Step 1 -  START
Step 2 -  C ← A + B + 10
Step 3 -  Stop

Ở đây chúng ta có ba biến A, B và C và một hằng số. Do đó S (P) = 1 + 3. Bây giờ, không gian phụ thuộc vào kiểu dữ liệu của các biến và kiểu hằng đã cho và nó sẽ được nhân lên tương ứng.

Thời gian phức tạp

Độ phức tạp thời gian của một thuật toán biểu thị lượng thời gian mà thuật toán yêu cầu để chạy đến khi hoàn thành. Yêu cầu về thời gian có thể được định nghĩa như một hàm số T (n), trong đó T (n) có thể được đo bằng số bước, miễn là mỗi bước tiêu thụ thời gian không đổi.

Ví dụ, phép cộng hai số nguyên n bit sẽ mất ncác bước. Do đó, tổng thời gian tính toán là T (n) = c ∗ n, trong đó c là thời gian thực hiện để cộng hai bit. Ở đây, chúng ta quan sát thấy rằng T (n) tăng tuyến tính khi kích thước đầu vào tăng lên.

Phân tích tiệm cận của một thuật toán đề cập đến việc xác định giới hạn / khung toán học đối với hiệu suất thời gian chạy của nó. Sử dụng phân tích tiệm cận, chúng ta rất có thể kết luận trường hợp tốt nhất, trường hợp trung bình và trường hợp xấu nhất của một thuật toán.

Phân tích tiệm cận bị ràng buộc đầu vào, tức là, nếu không có đầu vào cho thuật toán, nó được kết luận là hoạt động trong một thời gian không đổi. Ngoài "đầu vào" tất cả các yếu tố khác được coi là không đổi.

Phân tích tiệm cận đề cập đến việc tính toán thời gian chạy của bất kỳ hoạt động nào bằng các đơn vị tính toán. Ví dụ, thời gian chạy của một hoạt động được tính là f (n) và có thể đối với hoạt động khác, nó được tính là g (n ² ). Điều này có nghĩa là thời gian chạy hoạt động đầu tiên sẽ tăng tuyến tính với sự gia tăngn và thời gian chạy của hoạt động thứ hai sẽ tăng lên theo cấp số nhân khi ntăng. Tương tự, thời gian chạy của cả hai hoạt động sẽ gần như nhau nếun là nhỏ đáng kể.

Thông thường, thời gian theo yêu cầu của một thuật toán thuộc ba loại:

• Best Case - Thời gian tối thiểu cần thiết để thực hiện chương trình.

• Average Case - Thời gian trung bình cần thiết để thực hiện chương trình.

• Worst Case - Thời gian tối đa cần thiết để thực hiện chương trình.

Ký hiệu tiệm cận

Sau đây là các ký hiệu tiệm cận thường được sử dụng để tính độ phức tạp thời gian chạy của một thuật toán.

• Ο Kí hiệu
• Ký hiệu Ω
• θ Kí hiệu

Ký hiệu Big Oh, Ο

Kí hiệu Ο (n) là cách chính thức để biểu thị giới hạn trên của thời gian chạy thuật toán. Nó đo độ phức tạp thời gian trong trường hợp xấu nhất hoặc khoảng thời gian dài nhất mà một thuật toán có thể mất để hoàn thành.

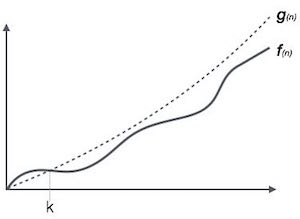
Ví dụ, đối với một hàm f(n)

Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that f(n) ≤ c.g(n) for all n > n0. }

Ký hiệu Omega, Ω

Kí hiệu Ω (n) là cách chính thức để biểu thị giới hạn dưới của thời gian chạy thuật toán. Nó đo độ phức tạp về thời gian của trường hợp tốt nhất hoặc khoảng thời gian tốt nhất mà một thuật toán có thể có để hoàn thành.

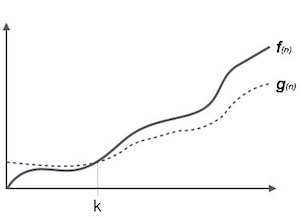
Ví dụ, đối với một hàm f(n)

Ω(f(n)) ≥ { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }

Ký hiệu Theta, θ

Kí hiệu θ (n) là cách chính thức để biểu thị cả giới hạn dưới và giới hạn trên của thời gian chạy thuật toán. Nó được biểu diễn như sau:

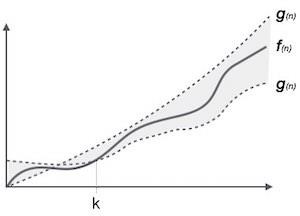
θ(f(n)) = { g(n) if and only if g(n) =  Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }

Kí hiệu tiệm cận phổ biến

Sau đây là danh sách một số ký hiệu tiệm cận phổ biến:

không thay đổi	-	Ο (1)
lôgarit	-	Ο (log n)
tuyến tính	-	Ο (n)
n log n	-	Ο (n log n)
bậc hai	-	Ο (n 2 )
khối	-	Ο (n 3 )
đa thức	-	n Ο (1)
số mũ	-	2 Ο (n)

Một thuật toán được thiết kế để đạt được giải pháp tối ưu cho một vấn đề nhất định. Trong cách tiếp cận thuật toán tham lam, các quyết định được đưa ra từ miền giải pháp đã cho. Vì tham lam, giải pháp gần nhất có vẻ cung cấp một giải pháp tối ưu được chọn.

Các thuật toán tham lam cố gắng tìm một giải pháp tối ưu được bản địa hóa, điều này cuối cùng có thể dẫn đến các giải pháp tối ưu hóa toàn cầu. Tuy nhiên, các thuật toán tham lam nói chung không cung cấp các giải pháp tối ưu hóa toàn cầu.

Đếm xu

Vấn đề này là tính đến một giá trị mong muốn bằng cách chọn những đồng xu ít nhất có thể và cách tiếp cận tham lam buộc thuật toán phải chọn đồng xu lớn nhất có thể. Nếu chúng tôi được cung cấp các đồng 1, 2, 5 và 10 và chúng tôi được yêu cầu đếm ₹ 18 thì thủ tục tham lam sẽ là -

• 1 - Chọn một đồng ₹ 10, số còn lại là 8

• 2 - Sau đó chọn một đồng ₹ 5, số còn lại là 3

• 3 - Sau đó chọn một ₹ 2 xu, số còn lại là 1

• 4 - Và cuối cùng, việc chọn một đồng 1 giải quyết được vấn đề

Mặc dù, nó có vẻ hoạt động tốt, với số lượng này, chúng ta chỉ cần chọn 4 đồng xu. Nhưng nếu chúng ta thay đổi một chút vấn đề thì cách tiếp cận tương tự có thể không tạo ra kết quả tối ưu như nhau.

Đối với hệ thống tiền tệ, nơi chúng ta có đồng xu có giá trị 1, 7, 10, việc đếm tiền cho giá trị 18 sẽ hoàn toàn tối ưu nhưng đối với số lượng như 15, nó có thể sử dụng nhiều đồng hơn mức cần thiết. Ví dụ, cách tiếp cận tham lam sẽ sử dụng 10 + 1 + 1 + 1 + 1 + 1, tổng cộng 6 xu. Trong khi vấn đề tương tự có thể được giải quyết bằng cách chỉ sử dụng 3 đồng tiền (7 + 7 + 1)

Do đó, chúng tôi có thể kết luận rằng cách tiếp cận tham lam chọn một giải pháp được tối ưu hóa ngay lập tức và có thể thất bại khi tối ưu hóa toàn cầu là mối quan tâm lớn.

Ví dụ

Hầu hết các thuật toán mạng sử dụng cách tiếp cận tham lam. Đây là danh sách một vài trong số họ -

• Vấn đề nhân viên bán hàng đi du lịch
• Thuật toán cây kéo dài tối thiểu của Prim
• Thuật toán cây kéo dài tối thiểu của Kruskal
• Thuật toán cây kéo dài tối thiểu của Dijkstra
• Biểu đồ - Tô màu bản đồ
• Đồ thị - Bìa đỉnh
• Vấn đề về Knapsack
• Vấn đề lên lịch công việc

Có rất nhiều vấn đề tương tự sử dụng phương pháp tham lam để tìm ra giải pháp tối ưu.

Trong cách tiếp cận phân chia và chinh phục, bài toán trong tay được chia thành các bài toán con nhỏ hơn và sau đó mỗi bài toán được giải quyết độc lập. Khi chúng ta tiếp tục chia các bài toán con thành các bài toán con nhỏ hơn, cuối cùng chúng ta có thể đạt đến một giai đoạn mà không thể chia thêm nữa. Những vấn đề con nhỏ nhất có thể có "nguyên tử" (phân số) được giải quyết. Lời giải của tất cả các bài toán con cuối cùng được hợp nhất để có được lời giải của bài toán ban đầu.

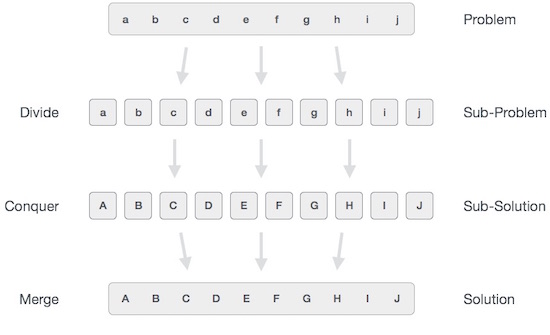
Nói chung, chúng ta có thể hiểu divide-and-conquer cách tiếp cận theo quy trình ba bước.

Chia / ngắt

Bước này liên quan đến việc chia nhỏ vấn đề thành các vấn đề phụ nhỏ hơn. Các vấn đề phụ nên đại diện cho một phần của vấn đề ban đầu. Bước này thường sử dụng một cách tiếp cận đệ quy để chia bài toán cho đến khi không có bài toán con nào có thể chia được nữa. Ở giai đoạn này, các vấn đề phụ trở thành nguyên tử về bản chất nhưng vẫn thể hiện một phần nào đó của vấn đề thực tế.

Chinh phục / Giải quyết

Bước này nhận được nhiều vấn đề nhỏ hơn cần giải quyết. Nói chung, ở cấp độ này, các vấn đề được coi là 'tự giải quyết'.

Hợp nhất / Kết hợp

Khi các bài toán con nhỏ hơn được giải quyết, giai đoạn này kết hợp chúng một cách đệ quy cho đến khi chúng tạo thành một giải pháp của bài toán ban đầu. Cách tiếp cận theo thuật toán này hoạt động một cách đệ quy và các bước chinh phục & hợp nhất hoạt động gần nhau đến mức chúng xuất hiện như một.

Ví dụ

Các thuật toán máy tính sau đây dựa trên divide-and-conquer cách tiếp cận lập trình -

• Hợp nhất Sắp xếp
• Sắp xếp nhanh chóng
• Tìm kiếm nhị phân
• Phép nhân ma trận của Strassen
• Cặp gần nhất (điểm)

Có nhiều cách khác nhau có sẵn để giải quyết bất kỳ vấn đề máy tính nào, nhưng những cách được đề cập là một ví dụ điển hình về phương pháp chia để trị.

Cách tiếp cận lập trình động tương tự như chia và chinh phục trong việc chia nhỏ vấn đề thành các vấn đề con nhỏ hơn và nhỏ hơn có thể. Nhưng không giống như, phân chia và chinh phục, những vấn đề phụ này không được giải quyết một cách độc lập. Thay vào đó, kết quả của các bài toán con nhỏ hơn này được ghi nhớ và sử dụng cho các bài toán con tương tự hoặc chồng chéo.

Lập trình động được sử dụng khi chúng ta gặp vấn đề, có thể được chia thành các vấn đề con tương tự, để có thể sử dụng lại kết quả của chúng. Hầu hết, các thuật toán này được sử dụng để tối ưu hóa. Trước khi giải bài toán con trong tay, thuật toán động sẽ cố gắng kiểm tra kết quả của các bài toán con đã giải trước đó. Các giải pháp của các vấn đề phụ được kết hợp để đạt được giải pháp tốt nhất.

Vì vậy, chúng ta có thể nói rằng -

• Vấn đề có thể được chia thành các vấn đề con chồng chéo nhỏ hơn.

• Một giải pháp tối ưu có thể đạt được bằng cách sử dụng một giải pháp tối ưu cho các vấn đề nhỏ hơn.

• Các thuật toán động sử dụng Memoization.

So sánh

Ngược lại với các thuật toán tham lam, trong đó tối ưu hóa cục bộ được giải quyết, các thuật toán động được thúc đẩy để tối ưu hóa tổng thể của vấn đề.

Ngược lại với các thuật toán phân chia và chinh phục, nơi các giải pháp được kết hợp để đạt được một giải pháp tổng thể, các thuật toán động sử dụng kết quả của một bài toán con nhỏ hơn và sau đó cố gắng tối ưu hóa một bài toán con lớn hơn. Các thuật toán động sử dụng Ghi nhớ để ghi nhớ kết quả đầu ra của các bài toán con đã được giải quyết.

Thí dụ

Các vấn đề máy tính sau đây có thể được giải quyết bằng cách sử dụng phương pháp lập trình động:

• Chuỗi số Fibonacci
• Knapsack vấn đề
• Tháp Hà Nội
• Tất cả các cặp đường đi ngắn nhất của Floyd-Warshall
• Con đường ngắn nhất của Dijkstra
• Lập kế hoạch dự án

Lập trình động có thể được sử dụng theo cả cách từ trên xuống và từ dưới lên. Và tất nhiên, hầu hết các trường hợp, tham khảo đầu ra giải pháp trước đó rẻ hơn so với tính toán lại về chu kỳ CPU.

Chương này giải thích các thuật ngữ cơ bản liên quan đến cấu trúc dữ liệu.

Định nghĩa dữ liệu

Định nghĩa dữ liệu xác định một dữ liệu cụ thể với các đặc điểm sau.

• Atomic - Định nghĩa nên xác định một khái niệm duy nhất.

• Traceable - Định nghĩa có thể được ánh xạ tới một số phần tử dữ liệu.

• Accurate - Định nghĩa phải rõ ràng.

• Clear and Concise - Định nghĩa phải dễ hiểu.

Đối tượng dữ liệu

Đối tượng dữ liệu đại diện cho một đối tượng có dữ liệu.

Loại dữ liệu

Kiểu dữ liệu là cách phân loại nhiều dạng dữ liệu khác nhau như số nguyên, chuỗi ký tự,… xác định các giá trị có thể sử dụng với kiểu dữ liệu tương ứng, kiểu các thao tác có thể thực hiện trên kiểu dữ liệu tương ứng. Có hai kiểu dữ liệu -

• Kiểu dữ liệu tích hợp
• Kiểu dữ liệu có nguồn gốc

Kiểu dữ liệu tích hợp

Những kiểu dữ liệu mà ngôn ngữ có hỗ trợ tích hợp được gọi là Kiểu dữ liệu tích hợp. Ví dụ: hầu hết các ngôn ngữ đều cung cấp các kiểu dữ liệu tích hợp sau.

• Integers
• Boolean (đúng, sai)
• Nổi (Số thập phân)
• Ký tự và chuỗi

Kiểu dữ liệu có nguồn gốc

Những kiểu dữ liệu độc lập với việc triển khai vì chúng có thể được triển khai theo cách này hay cách khác được gọi là kiểu dữ liệu dẫn xuất. Các kiểu dữ liệu này thường được xây dựng bằng cách kết hợp các kiểu dữ liệu chính hoặc tích hợp và các hoạt động liên quan trên chúng. Ví dụ -

• List
• Array
• Stack
• Queue

Hoạt động cơ bản

Dữ liệu trong cấu trúc dữ liệu được xử lý bằng các hoạt động nhất định. Cấu trúc dữ liệu cụ thể được chọn phần lớn phụ thuộc vào tần suất của hoạt động cần được thực hiện trên cấu trúc dữ liệu.

• Traversing
• Searching
• Insertion
• Deletion
• Sorting
• Merging

Mảng là một vùng chứa có thể chứa một số lượng cố định các mục và các mục này phải cùng loại. Hầu hết các cấu trúc dữ liệu sử dụng mảng để triển khai các thuật toán của chúng. Sau đây là các thuật ngữ quan trọng để hiểu khái niệm về Mảng.

• Element - Mỗi mục được lưu trong một mảng được gọi là một phần tử.

• Index - Mỗi vị trí của một phần tử trong mảng có một chỉ số số, dùng để xác định phần tử đó.

Biểu diễn mảng

Mảng có thể được khai báo theo nhiều cách khác nhau trong các ngôn ngữ khác nhau. Để minh họa, hãy lấy khai báo mảng C.

Mảng có thể được khai báo theo nhiều cách khác nhau trong các ngôn ngữ khác nhau. Để minh họa, hãy lấy khai báo mảng C.

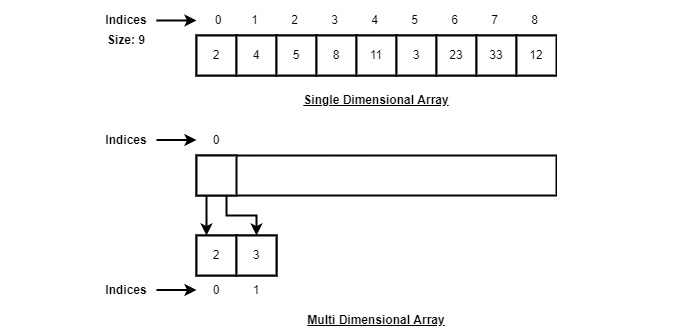
Theo hình minh họa ở trên, sau đây là những điểm quan trọng cần được xem xét.

• Chỉ mục bắt đầu bằng 0.

• Độ dài mảng là 10 có nghĩa là nó có thể lưu trữ 10 phần tử.

• Mỗi phần tử có thể được truy cập thông qua chỉ mục của nó. Ví dụ, chúng ta có thể tìm nạp một phần tử ở chỉ số 6 là 9.

Hoạt động cơ bản

Sau đây là các hoạt động cơ bản được hỗ trợ bởi một mảng.

• Traverse - in lần lượt tất cả các phần tử của mảng.

• Insertion - Thêm một phần tử tại chỉ mục đã cho.

• Deletion - Xóa một phần tử tại chỉ mục đã cho.

• Search - Tìm kiếm một phần tử bằng cách sử dụng chỉ số đã cho hoặc theo giá trị.

• Update - Cập nhật một phần tử tại chỉ mục nhất định.

Trong C, khi một mảng được khởi tạo với kích thước, thì nó sẽ gán các giá trị mặc định cho các phần tử của nó theo thứ tự sau.

Loại dữ liệu	Giá trị mặc định
bool	sai
char	0
int	0
Phao nổi	0,0
gấp đôi	0,0f
vô hiệu
wchar_t	0

Hoạt động theo chiều ngang

Thao tác này là duyệt qua các phần tử của một mảng.

Thí dụ

Chương trình sau sẽ duyệt và in các phần tử của một mảng:

#include <stdio.h>
main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;   
   printf("The original array elements are :\n");
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Khi chúng tôi biên dịch và thực thi chương trình trên, nó tạo ra kết quả sau:

Đầu ra

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8

Thao tác chèn

Thao tác chèn là chèn một hoặc nhiều phần tử dữ liệu vào một mảng. Dựa trên yêu cầu, một phần tử mới có thể được thêm vào đầu, cuối hoặc bất kỳ chỉ mục nhất định nào của mảng.

Ở đây, chúng tôi thấy một triển khai thực tế của hoạt động chèn, nơi chúng tôi thêm dữ liệu vào cuối mảng -

Thí dụ

Sau đây là việc triển khai thuật toán trên:

#include <stdio.h>

main() {
   int LA[] = {1,3,5,7,8};
   int item = 10, k = 3, n = 5;
   int i = 0, j = n;
   
   printf("The original array elements are :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }

   n = n + 1;
	
   while( j >= k) {
      LA[j+1] = LA[j];
      j = j - 1;
   }

   LA[k] = item;

   printf("The array elements after insertion :\n");

   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Khi chúng tôi biên dịch và thực thi chương trình trên, nó tạo ra kết quả sau:

Đầu ra

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after insertion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 10 
LA[4] = 7 
LA[5] = 8

Để biết các biến thể khác của thao tác chèn mảng, hãy nhấp vào đây

Thao tác xóa

Xóa đề cập đến việc xóa một phần tử hiện có khỏi mảng và tổ chức lại tất cả các phần tử của một mảng.

Thuật toán

Xem xét LA là một mảng tuyến tính với N các yếu tố và K là một số nguyên dương sao cho K<=N. Sau đây là thuật toán xóa một phần tử có sẵn ở vị trí ^thứ K của LA.

1. Start
2. Set J = K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J] = LA[J + 1]
5. Set J = J+1
6. Set N = N-1
7. Stop

Thí dụ

Sau đây là việc triển khai thuật toán trên:

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   j = k;
	
   while( j < n) {
      LA[j-1] = LA[j];
      j = j + 1;
   }
	
   n = n -1;
   
   printf("The array elements after deletion :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Khi chúng tôi biên dịch và thực thi chương trình trên, nó tạo ra kết quả sau:

Đầu ra

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after deletion :
LA[0] = 1 
LA[1] = 3 
LA[2] = 7 
LA[3] = 8

Hoạt động tìm kiếm

Bạn có thể thực hiện tìm kiếm một phần tử mảng dựa trên giá trị hoặc chỉ mục của nó.

Thuật toán

Xem xét LA là một mảng tuyến tính với N các yếu tố và K là một số nguyên dương sao cho K<=N. Sau đây là thuật toán để tìm một phần tử có giá trị là ITEM bằng cách sử dụng tìm kiếm tuần tự.

1. Start
2. Set J = 0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +1
6. PRINT J, ITEM
7. Stop

Thí dụ

Sau đây là việc triển khai thuật toán trên:

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int item = 5, n = 5;
   int i = 0, j = 0;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   while( j < n){
      if( LA[j] == item ) {
         break;
      }
		
      j = j + 1;
   }
	
   printf("Found element %d at position %d\n", item, j+1);
}

Khi chúng tôi biên dịch và thực thi chương trình trên, nó tạo ra kết quả sau:

Đầu ra

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
Found element 5 at position 3

Cập nhật hoạt động

Hoạt động cập nhật đề cập đến việc cập nhật một phần tử hiện có từ mảng tại một chỉ mục nhất định.

Thuật toán

Xem xét LA là một mảng tuyến tính với N các yếu tố và K là một số nguyên dương sao cho K<=N. Sau đây là thuật toán để cập nhật một phần tử có sẵn ở vị trí ^thứ K của LA.

1. Start
2. Set LA[K-1] = ITEM
3. Stop

Thí dụ

Sau đây là việc triển khai thuật toán trên:

#include <stdio.h>

void main() {
   int LA[] = {1,3,5,7,8};
   int k = 3, n = 5, item = 10;
   int i, j;
   
   printf("The original array elements are :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
    
   LA[k-1] = item;

   printf("The array elements after updation :\n");
	
   for(i = 0; i<n; i++) {
      printf("LA[%d] = %d \n", i, LA[i]);
   }
}

Khi chúng tôi biên dịch và thực thi chương trình trên, nó tạo ra kết quả sau:

Đầu ra

The original array elements are :
LA[0] = 1 
LA[1] = 3 
LA[2] = 5 
LA[3] = 7 
LA[4] = 8 
The array elements after updation :
LA[0] = 1 
LA[1] = 3 
LA[2] = 10 
LA[3] = 7 
LA[4] = 8

Danh sách liên kết là một chuỗi các cấu trúc dữ liệu, được kết nối với nhau thông qua các liên kết.

Danh sách liên kết là một chuỗi các liên kết chứa các mục. Mỗi liên kết chứa một kết nối đến một liên kết khác. Danh sách liên kết là cấu trúc dữ liệu được sử dụng nhiều thứ hai sau mảng. Sau đây là các thuật ngữ quan trọng để hiểu khái niệm về Danh sách liên kết.

• Link - Mỗi liên kết của danh sách liên kết có thể lưu trữ một dữ liệu gọi là phần tử.

• Next - Mỗi liên kết của một danh sách liên kết chứa một liên kết đến liên kết tiếp theo được gọi là Next.

• LinkedList - Một Danh sách được Liên kết chứa liên kết kết nối đến liên kết đầu tiên được gọi là First.

Trình bày danh sách được liên kết

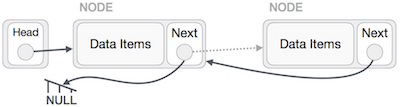
Danh sách được liên kết có thể được hình dung như một chuỗi các nút, nơi mọi nút đều trỏ đến nút tiếp theo.

Theo hình minh họa ở trên, sau đây là những điểm quan trọng cần được xem xét.

• Danh sách được Liên kết chứa một phần tử liên kết được gọi là đầu tiên.

• Mỗi liên kết mang (các) trường dữ liệu và một trường liên kết được gọi là tiếp theo.

• Mỗi liên kết được liên kết với liên kết tiếp theo của nó bằng cách sử dụng liên kết tiếp theo của nó.

• Liên kết cuối cùng mang một liên kết là null để đánh dấu phần cuối của danh sách.

Các loại danh sách được liên kết

Sau đây là các loại danh sách liên kết.

• Simple Linked List - Điều hướng mục chỉ được chuyển tiếp.

• Doubly Linked List - Các mục có thể được điều hướng về phía trước và phía sau.

• Circular Linked List - Mục cuối cùng chứa liên kết của phần tử đầu tiên là tiếp theo và phần tử đầu tiên có liên kết đến phần tử cuối cùng như trước.

Hoạt động cơ bản

Sau đây là các thao tác cơ bản được hỗ trợ bởi một danh sách.

• Insertion - Thêm một phần tử vào đầu danh sách.

• Deletion - Xóa một phần tử ở đầu danh sách.

• Display - Hiển thị danh sách đầy đủ.

• Search - Tìm kiếm một phần tử bằng cách sử dụng khóa đã cho.

• Delete - Xóa một phần tử bằng cách sử dụng khóa đã cho.

Thao tác chèn

Thêm một nút mới trong danh sách được liên kết là một hoạt động nhiều hơn một bước. Chúng ta sẽ tìm hiểu điều này với các sơ đồ ở đây. Đầu tiên, tạo một nút bằng cách sử dụng cùng một cấu trúc và tìm vị trí mà nó phải được chèn vào.

Hãy tưởng tượng rằng chúng ta đang chèn một nút B (NewNode), giữa A (LeftNode) và C(RightNode). Sau đó trỏ B.next vào C -

NewNode.next −> RightNode;

Nó sẽ trông như thế này -

Bây giờ, nút tiếp theo ở bên trái sẽ trỏ đến nút mới.

LeftNode.next −> NewNode;

Điều này sẽ đặt nút mới ở giữa hai nút. Danh sách mới sẽ trông như thế này -

Các bước tương tự nên được thực hiện nếu nút đang được chèn vào đầu danh sách. Trong khi chèn nó vào cuối, nút cuối cùng thứ hai của danh sách phải trỏ đến nút mới và nút mới sẽ trỏ đến NULL.

Thao tác xóa

Xóa cũng là một quá trình nhiều hơn một bước. Chúng ta sẽ học bằng cách biểu diễn bằng hình ảnh. Đầu tiên, xác định vị trí nút đích sẽ bị xóa bằng cách sử dụng các thuật toán tìm kiếm.

Nút bên trái (trước đó) của nút đích bây giờ sẽ trỏ đến nút tiếp theo của nút đích -

LeftNode.next −> TargetNode.next;

Thao tác này sẽ xóa liên kết đã trỏ đến nút đích. Bây giờ, bằng cách sử dụng đoạn mã sau, chúng ta sẽ xóa những gì mà nút đích đang trỏ đến.

TargetNode.next −> NULL;

Chúng ta cần sử dụng nút đã xóa. Chúng ta có thể giữ nó trong bộ nhớ nếu không, chúng ta có thể chỉ cần phân bổ bộ nhớ và xóa hoàn toàn nút đích.

Hoạt động ngược lại

Hoạt động này là một trong những triệt để. Chúng ta cần làm cho nút cuối cùng được trỏ đến bởi nút đầu và đảo ngược toàn bộ danh sách được liên kết.

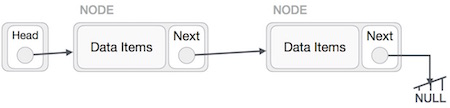
Đầu tiên, chúng tôi đi đến cuối danh sách. Nó sẽ được trỏ đến NULL. Bây giờ, chúng ta sẽ làm cho nó trỏ đến nút trước của nó -

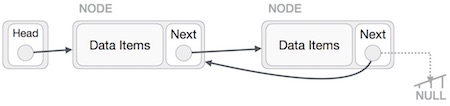
Chúng ta phải đảm bảo rằng nút cuối cùng không phải là nút cuối cùng. Vì vậy, chúng ta sẽ có một số nút tạm thời, trông giống như nút đầu trỏ đến nút cuối cùng. Bây giờ, chúng ta sẽ làm cho tất cả các nút bên trái lần lượt trỏ đến các nút trước của chúng.

Ngoại trừ nút (nút đầu tiên) được trỏ bởi nút đầu, tất cả các nút phải trỏ đến nút tiền nhiệm, biến chúng thành nút kế nhiệm mới của chúng. Nút đầu tiên sẽ trỏ đến NULL.

Chúng tôi sẽ làm cho nút đầu trỏ đến nút đầu tiên mới bằng cách sử dụng nút tạm thời.

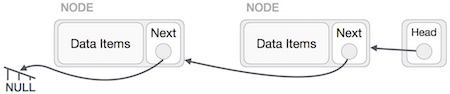
Danh sách liên kết hiện đã được đảo ngược. Để xem triển khai danh sách liên kết bằng ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Danh sách được liên kết đôi là một biến thể của danh sách được liên kết trong đó có thể điều hướng theo cả hai cách, dễ dàng chuyển tiếp và lùi lại so với Danh sách được liên kết đơn lẻ. Sau đây là các thuật ngữ quan trọng để hiểu khái niệm về danh sách liên kết kép.

• Link - Mỗi liên kết của danh sách liên kết có thể lưu trữ một dữ liệu gọi là phần tử.

• Next - Mỗi liên kết của một danh sách liên kết chứa một liên kết đến liên kết tiếp theo được gọi là Next.

• Prev - Mỗi liên kết của một danh sách liên kết chứa một liên kết đến liên kết trước đó được gọi là Prev.

• LinkedList - Một Danh sách được Liên kết chứa liên kết kết nối đến liên kết đầu tiên được gọi là Đầu tiên và đến liên kết cuối cùng được gọi là Cuối cùng.

Trình bày danh sách được liên kết gấp đôi

Theo hình minh họa ở trên, sau đây là những điểm quan trọng cần được xem xét.

• Danh sách được liên kết đôi chứa một phần tử liên kết được gọi là đầu tiên và cuối cùng.

• Mỗi liên kết mang (các) trường dữ liệu và hai trường liên kết được gọi là tiếp theo và trước.

• Mỗi liên kết được liên kết với liên kết tiếp theo của nó bằng cách sử dụng liên kết tiếp theo của nó.

• Mỗi liên kết được liên kết với liên kết trước của nó bằng cách sử dụng liên kết trước của nó.

• Liên kết cuối cùng mang một liên kết là null để đánh dấu phần cuối của danh sách.

Hoạt động cơ bản

Sau đây là các thao tác cơ bản được hỗ trợ bởi một danh sách.

• Insertion - Thêm một phần tử vào đầu danh sách.

• Deletion - Xóa một phần tử ở đầu danh sách.

• Insert Last - Thêm một phần tử vào cuối danh sách.

• Delete Last - Xóa một phần tử khỏi cuối danh sách.

• Insert After - Thêm một phần tử sau một mục của danh sách.

• Delete - Xóa một phần tử khỏi danh sách bằng phím.

• Display forward - Hiển thị danh sách đầy đủ theo cách chuyển tiếp.

• Display backward - Hiển thị danh sách đầy đủ theo cách lùi.

Thao tác chèn

Đoạn mã sau minh họa thao tác chèn vào đầu danh sách được liên kết kép.

Thí dụ

//insert link at the first location
void insertFirst(int key, int data) {

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
	
   if(isEmpty()) {
      //make it the last link
      last = link;
   } else {
      //update first prev link
      head->prev = link;
   }

   //point it to old first link
   link->next = head;
	
   //point first to new first link
   head = link;
}

Thao tác xóa

Đoạn mã sau minh họa thao tác xóa ở đầu danh sách được liên kết kép.

Thí dụ

//delete first item
struct node* deleteFirst() {

   //save reference to first link
   struct node *tempLink = head;
	
   //if only one link
   if(head->next == NULL) {
      last = NULL;
   } else {
      head->next->prev = NULL;
   }
	
   head = head->next;
	
   //return the deleted link
   return tempLink;
}

Chèn khi kết thúc hoạt động

Đoạn mã sau minh họa thao tác chèn ở vị trí cuối cùng của danh sách được liên kết kép.

Thí dụ

//insert link at the last location
void insertLast(int key, int data) {

   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data = data;
	
   if(isEmpty()) {
      //make it the last link
      last = link;
   } else {
      //make link a new last link
      last->next = link;     
      
      //mark old last node as prev of new link
      link->prev = last;
   }

   //point last to new last node
   last = link;
}

Để xem cách triển khai bằng ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Danh sách liên kết hình tròn là một biến thể của Danh sách liên kết trong đó phần tử đầu tiên trỏ đến phần tử cuối cùng và phần tử cuối cùng trỏ đến phần tử đầu tiên. Cả Danh sách liên kết đơn và Danh sách liên kết kép đều có thể được tạo thành một danh sách liên kết vòng.

Danh sách liên kết Singly dưới dạng vòng tròn

Trong danh sách được liên kết đơn lẻ, con trỏ tiếp theo của nút cuối cùng trỏ đến nút đầu tiên.

Danh sách được liên kết gấp đôi dưới dạng hình tròn

Trong danh sách liên kết kép, con trỏ tiếp theo của nút cuối cùng trỏ đến nút đầu tiên và con trỏ trước đó của nút đầu tiên trỏ đến nút cuối cùng tạo thành vòng tròn theo cả hai hướng.

Theo hình minh họa ở trên, sau đây là những điểm quan trọng cần được xem xét.

• Liên kết tiếp theo của liên kết cuối cùng trỏ đến liên kết đầu tiên của danh sách trong cả hai trường hợp danh sách liên kết đơn và liên kết kép.

• Liên kết trước của liên kết đầu tiên trỏ đến cuối cùng của danh sách trong trường hợp danh sách được liên kết kép.

Hoạt động cơ bản

Sau đây là các thao tác quan trọng được hỗ trợ bởi danh sách vòng tròn.

• insert - Chèn một phần tử vào đầu danh sách.

• delete - Xóa một phần tử khỏi đầu danh sách.

• display - Hiển thị danh sách.

Thao tác chèn

Đoạn mã sau minh họa thao tác chèn trong danh sách liên kết vòng dựa trên danh sách liên kết đơn.

Thí dụ

//insert link at the first location
void insertFirst(int key, int data) {
   //create a link
   struct node *link = (struct node*) malloc(sizeof(struct node));
   link->key = key;
   link->data= data;
	
   if (isEmpty()) {
      head = link;
      head->next = head;
   } else {
      //point it to old first node
      link->next = head;
		
      //point first to new first node
      head = link;
   }   
}

Thao tác xóa

Đoạn mã sau minh họa thao tác xóa trong danh sách liên kết vòng dựa trên danh sách liên kết đơn.

//delete first item
struct node * deleteFirst() {
   //save reference to first link
   struct node *tempLink = head;
	
   if(head->next == head) {  
      head = NULL;
      return tempLink;
   }     

   //mark next to first link as first 
   head = head->next;
	
   //return the deleted link
   return tempLink;
}

Hoạt động danh sách hiển thị

Đoạn mã sau minh họa thao tác hiển thị danh sách trong danh sách liên kết vòng.

//display the list
void printList() {
   struct node *ptr = head;
   printf("\n[ ");
	
   //start from the beginning
   if(head != NULL) {
      while(ptr->next != ptr) {     
         printf("(%d,%d) ",ptr->key,ptr->data);
         ptr = ptr->next;
      }
   }
	
   printf(" ]");
}

Để biết về cách triển khai của nó trong ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Ngăn xếp là một kiểu dữ liệu trừu tượng (ADT), thường được sử dụng trong hầu hết các ngôn ngữ lập trình. Nó được đặt tên là ngăn xếp vì nó hoạt động giống như một ngăn xếp trong thế giới thực, chẳng hạn - một bộ bài hoặc một đống đĩa, v.v.

Một ngăn xếp trong thế giới thực chỉ cho phép các hoạt động ở một đầu. Ví dụ, chúng ta chỉ có thể đặt hoặc lấy thẻ hoặc đĩa ở trên cùng của ngăn xếp. Tương tự như vậy, Stack ADT chỉ cho phép tất cả các hoạt động dữ liệu ở một đầu. Tại bất kỳ thời điểm nào, chúng tôi chỉ có thể truy cập phần tử trên cùng của ngăn xếp.

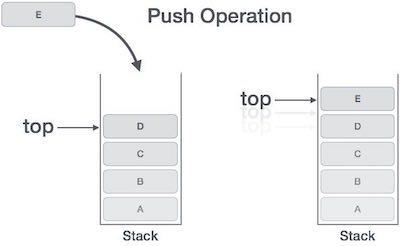
Tính năng này làm cho nó trở thành cấu trúc dữ liệu LIFO. LIFO là viết tắt của Last-in-first-out. Ở đây, phần tử được đặt (chèn hoặc thêm) cuối cùng, được truy cập đầu tiên. Trong thuật ngữ ngăn xếp, hoạt động chèn được gọi làPUSH hoạt động và hoạt động loại bỏ được gọi là POP hoạt động.

Biểu diễn ngăn xếp

Sơ đồ sau mô tả một ngăn xếp và các hoạt động của nó:

Một ngăn xếp có thể được thực hiện bằng Mảng, Cấu trúc, Con trỏ và Danh sách Liên kết. Ngăn xếp có thể có kích thước cố định hoặc có thể có cảm giác thay đổi kích thước động. Ở đây, chúng ta sẽ triển khai ngăn xếp bằng cách sử dụng các mảng, làm cho nó trở thành một triển khai ngăn xếp có kích thước cố định.

Hoạt động cơ bản

Các hoạt động ngăn xếp có thể liên quan đến việc khởi tạo ngăn xếp, sử dụng nó và sau đó khử khởi tạo nó. Ngoài những nội dung cơ bản này, ngăn xếp được sử dụng cho hai hoạt động chính sau:

• push() - Đẩy (lưu trữ) một phần tử trên ngăn xếp.

• pop() - Loại bỏ (truy cập) một phần tử khỏi ngăn xếp.

Khi dữ liệu được PUSHed vào ngăn xếp.

Để sử dụng ngăn xếp một cách hiệu quả, chúng ta cũng cần kiểm tra trạng thái của ngăn xếp. Với mục đích tương tự, chức năng sau được thêm vào ngăn xếp:

• peek() - lấy phần tử dữ liệu trên cùng của ngăn xếp mà không cần xóa nó.

• isFull() - kiểm tra xem ngăn xếp đã đầy chưa.

• isEmpty() - kiểm tra xem ngăn xếp có trống không.

Tại mọi thời điểm, chúng tôi duy trì một con trỏ đến dữ liệu PUSHed cuối cùng trên ngăn xếp. Vì con trỏ này luôn đại diện cho phần trên cùng của ngăn xếp, do đó có têntop. Cáctop con trỏ cung cấp giá trị cao nhất của ngăn xếp mà không thực sự loại bỏ nó.

Trước tiên, chúng ta nên tìm hiểu về các thủ tục để hỗ trợ các hàm ngăn xếp -

nhìn trộm ()

Thuật toán của hàm peek () -

begin procedure peek
   return stack[top]
end procedure

Thực hiện hàm peek () trong ngôn ngữ lập trình C -

Example

int peek() {
   return stack[top];
}

isfull ()

Thuật toán của hàm isfull () -

begin procedure isfull

   if top equals to MAXSIZE
      return true
   else
      return false
   endif
   
end procedure

Thực hiện hàm isfull () trong ngôn ngữ lập trình C.

Example

bool isfull() {
   if(top == MAXSIZE)
      return true;
   else
      return false;
}

isempty ()

Thuật toán của hàm isempty () -

begin procedure isempty

   if top less than 1
      return true
   else
      return false
   endif
   
end procedure

Việc triển khai hàm isempty () trong ngôn ngữ lập trình C hơi khác một chút. Chúng tôi khởi tạo đỉnh ở -1, vì chỉ số trong mảng bắt đầu từ 0. Vì vậy, chúng tôi kiểm tra xem đỉnh có dưới 0 hay -1 để xác định xem ngăn xếp có trống hay không. Đây là mã -

Example

bool isempty() {
   if(top == -1)
      return true;
   else
      return false;
}

Hoạt động đẩy

Quá trình đưa một phần tử dữ liệu mới vào ngăn xếp được gọi là Hoạt động Đẩy. Hoạt động đẩy bao gồm một loạt các bước -

• Step 1 - Kiểm tra xem chồng có đầy không.

• Step 2 - Nếu ngăn xếp đầy, tạo ra lỗi và thoát.

• Step 3 - Nếu ngăn xếp không đầy, tăng top để chỉ không gian trống tiếp theo.

• Step 4 - Thêm phần tử dữ liệu vào vị trí ngăn xếp, nơi đỉnh đang trỏ.

• Step 5 - Trả lại thành công.

Nếu danh sách liên kết được sử dụng để triển khai ngăn xếp, thì ở bước 3, chúng ta cần cấp phát không gian động.

Thuật toán cho hoạt động PUSH

Một thuật toán đơn giản cho hoạt động Đẩy có thể được suy ra như sau:

begin procedure push: stack, data

   if stack is full
      return null
   endif
   
   top ← top + 1
   stack[top] ← data

end procedure

Việc thực hiện thuật toán này trong C, rất dễ dàng. Xem đoạn mã sau -

Example

void push(int data) {
   if(!isFull()) {
      top = top + 1;   
      stack[top] = data;
   } else {
      printf("Could not insert data, Stack is full.\n");
   }
}

Hoạt động Pop

Truy cập nội dung trong khi xóa nội dung đó khỏi ngăn xếp, được gọi là Thao tác bật. Trong triển khai mảng của thao tác pop (), phần tử dữ liệu không thực sự bị xóa, thay vào đótopđược giảm xuống vị trí thấp hơn trong ngăn xếp để trỏ đến giá trị tiếp theo. Nhưng trong triển khai danh sách liên kết, pop () thực sự loại bỏ phần tử dữ liệu và phân bổ không gian bộ nhớ.

Hoạt động Pop có thể bao gồm các bước sau:

• Step 1 - Kiểm tra xem ngăn xếp có trống không.

• Step 2 - Nếu ngăn xếp trống, tạo ra lỗi và thoát.

• Step 3 - Nếu ngăn xếp không trống, hãy truy cập vào phần tử dữ liệu mà tại đó top đang trỏ.

• Step 4 - Giảm giá trị của top 1.

• Step 5 - Trả lại thành công.

Thuật toán cho hoạt động pop

Một thuật toán đơn giản cho hoạt động Pop có thể được suy ra như sau:

begin procedure pop: stack

   if stack is empty
      return null
   endif
   
   data ← stack[top]
   top ← top - 1
   return data

end procedure

Việc triển khai thuật toán này trong C, như sau:

Example

int pop(int data) {

   if(!isempty()) {
      data = stack[top];
      top = top - 1;   
      return data;
   } else {
      printf("Could not retrieve data, Stack is empty.\n");
   }
}

Để có một chương trình ngăn xếp hoàn chỉnh bằng ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Cách viết biểu thức số học được gọi là notation. Một biểu thức số học có thể được viết bằng ba ký hiệu khác nhau nhưng tương đương, tức là, không làm thay đổi bản chất hoặc đầu ra của một biểu thức. Các ký hiệu này là -

• Ký hiệu infix
• Ký hiệu tiền tố (tiếng Ba Lan)
• Ký hiệu Postfix (Reverse-Polish)

Các ký hiệu này được đặt tên như cách chúng sử dụng toán tử trong biểu thức. Chúng ta sẽ tìm hiểu tương tự ở đây trong chương này.

Ký hiệu infix

Chúng tôi viết biểu thức trong infix ký hiệu, ví dụ a - b + c, trong đó các toán tử được sử dụng in-giữa các toán hạng. Con người chúng ta có thể dễ dàng đọc, viết và nói bằng ký hiệu infix nhưng điều này không tốt với các thiết bị máy tính. Một thuật toán để xử lý ký hiệu infix có thể khó và tốn kém về thời gian và không gian tiêu thụ.

Ký hiệu tiền tố

Trong ký hiệu này, toán tử là prefixed thành toán hạng, tức là toán tử được viết trước toán hạng. Ví dụ,+ab. Điều này tương đương với ký hiệu infix của nóa + b. Ký hiệu tiền tố còn được gọi làPolish Notation.

Ký hiệu Postfix

Kiểu ký hiệu này được gọi là Reversed Polish Notation. Trong kiểu ký hiệu này, toán tử làpostfixed cho các toán hạng tức là, toán tử được viết sau các toán hạng. Ví dụ,ab+. Điều này tương đương với ký hiệu infix của nóa + b.

Bảng sau đây cố gắng chỉ ra ngắn gọn sự khác biệt trong cả ba ký hiệu:

Sr.No.	Ký hiệu infix	Ký hiệu tiền tố	Ký hiệu Postfix
1	a + b	+ ab	ab +
2	(a + b) ∗ c	∗ + abc	ab + c ∗
3	a ∗ (b + c)	∗ a + bc	abc + ∗
4	a / b + c / d	+ / ab / cd	ab / cd / +
5	(a + b) ∗ (c + d)	∗ + ab + cd	ab + cd + ∗
6	((a + b) ∗ c) - d	- ∗ + abcd	ab + c ∗ d -

Phân tích cú pháp biểu thức

Như chúng ta đã thảo luận, đây không phải là một cách hiệu quả để thiết kế một thuật toán hoặc chương trình để phân tích cú pháp các ký hiệu infix. Thay vào đó, các ký hiệu tiền tố này đầu tiên được chuyển đổi thành ký hiệu hậu tố hoặc tiền tố và sau đó được tính toán.

Để phân tích cú pháp bất kỳ biểu thức số học nào, chúng ta cũng cần quan tâm đến mức độ ưu tiên của toán tử và tính kết hợp.

Quyền ưu tiên

Khi một toán hạng nằm giữa hai toán tử khác nhau, toán tử nào sẽ lấy toán hạng trước, được quyết định bởi sự ưu tiên của một toán tử so với những toán tử khác. Ví dụ -

Vì phép toán nhân được ưu tiên hơn phép cộng nên b * c sẽ được đánh giá trước. Bảng ưu tiên toán tử được cung cấp sau.

Sự liên kết

Tính liên kết mô tả quy tắc trong đó các toán tử có cùng mức độ ưu tiên xuất hiện trong một biểu thức. Ví dụ, trong biểu thức a + b - c, cả + và - đều có cùng mức độ ưu tiên, thì phần nào của biểu thức sẽ được đánh giá trước, được xác định bởi tính kết hợp của các toán tử đó. Ở đây, cả + và - đều có liên quan trái, vì vậy biểu thức sẽ được đánh giá là(a + b) − c.

Mức độ ưu tiên và tính liên kết xác định thứ tự đánh giá một biểu thức. Sau đây là bảng liên kết và ưu tiên toán tử (cao nhất đến thấp nhất):

Sr.No.	Nhà điều hành	Quyền ưu tiên	Sự liên kết
1	Luỹ thừa ^	Cao nhất	Liên kết phù hợp
2	Phép nhân (∗) & Phép chia (/)	Cao thứ hai	Liên kết trái
3	Phép cộng (+) & Phép trừ (-)	Thấp nhất	Liên kết trái

Bảng trên cho thấy hành vi mặc định của các toán tử. Tại bất kỳ thời điểm nào trong đánh giá biểu thức, thứ tự có thể được thay đổi bằng cách sử dụng dấu ngoặc đơn. Ví dụ -

Trong a + b*c, phần biểu hiện b*csẽ được đánh giá đầu tiên, với phép nhân được ưu tiên hơn phép cộng. Ở đây chúng tôi sử dụng dấu ngoặc đơn choa + b được đánh giá đầu tiên, như (a + b)*c.

Thuật toán đánh giá Postfix

Bây giờ chúng ta sẽ xem xét thuật toán về cách đánh giá ký hiệu hậu tố -

Step 1 − scan the expression from left to right 
Step 2 − if it is an operand push it to stack 
Step 3 − if it is an operator pull operand from stack and perform operation 
Step 4 − store the output of step 3, back to stack 
Step 5 − scan the expression until all operands are consumed 
Step 6 − pop the stack and perform operation

Để xem cách triển khai bằng ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Queue là một cấu trúc dữ liệu trừu tượng, hơi giống với Stacks. Không giống như ngăn xếp, một hàng đợi được mở ở cả hai đầu của nó. Một đầu luôn dùng để chèn dữ liệu (enqueue) và đầu kia dùng để xóa dữ liệu (dequeue). Hàng đợi tuân theo phương pháp First-In-First-Out, tức là mục dữ liệu được lưu trước sẽ được truy cập trước.

Ví dụ trong thế giới thực về hàng đợi có thể là đường một chiều có một làn xe, nơi xe đi vào trước, ra trước. Có thể thấy nhiều ví dụ thực tế hơn như xếp hàng ở cửa sổ soát vé và trạm dừng xe buýt.

Trình bày hàng đợi

Như bây giờ chúng ta hiểu rằng trong hàng đợi, chúng ta truy cập cả hai đầu vì những lý do khác nhau. Sơ đồ sau được đưa ra dưới đây cố gắng giải thích biểu diễn hàng đợi dưới dạng cấu trúc dữ liệu:

Giống như trong ngăn xếp, hàng đợi cũng có thể được thực hiện bằng Mảng, Danh sách được liên kết, Con trỏ và Cấu trúc. Để đơn giản, chúng ta sẽ triển khai các hàng đợi bằng cách sử dụng mảng một chiều.

Hoạt động cơ bản

Các hoạt động hàng đợi có thể liên quan đến việc khởi tạo hoặc xác định hàng đợi, sử dụng nó, và sau đó xóa hoàn toàn nó khỏi bộ nhớ. Ở đây chúng tôi sẽ cố gắng hiểu các hoạt động cơ bản liên quan đến hàng đợi -

• enqueue() - thêm (lưu trữ) một mục vào hàng đợi.

• dequeue() - xóa (truy cập) một mục khỏi hàng đợi.

Cần thêm một số chức năng để làm cho hoạt động hàng đợi nói trên hiệu quả. Đây là -

• peek() - Lấy phần tử ở phía trước hàng đợi mà không cần loại bỏ nó.

• isfull() - Kiểm tra xem hàng đợi đã đầy chưa.

• isempty() - Kiểm tra xem hàng đợi có trống không.

Trong hàng đợi, chúng tôi luôn xếp hàng (hoặc truy cập) dữ liệu, được trỏ bởi front con trỏ và trong khi đánh dấu (hoặc lưu trữ) dữ liệu trong hàng đợi, chúng tôi sẽ trợ giúp rear con trỏ.

Đầu tiên chúng ta hãy tìm hiểu về các chức năng hỗ trợ của hàng đợi -

nhìn trộm ()

Chức năng này giúp xem dữ liệu tại frontcủa hàng đợi. Thuật toán của hàm peek () như sau:

Algorithm

begin procedure peek
   return queue[front]
end procedure

Thực hiện hàm peek () trong ngôn ngữ lập trình C -

Example

int peek() {
   return queue[front];
}

isfull ()

Vì chúng tôi đang sử dụng mảng một chiều để triển khai hàng đợi, chúng tôi chỉ cần kiểm tra xem con trỏ phía sau có đạt đến MAXSIZE hay không để xác định rằng hàng đợi đã đầy. Trong trường hợp chúng tôi duy trì hàng đợi trong danh sách liên kết vòng tròn, thuật toán sẽ khác. Thuật toán của hàm isfull () -

Algorithm

begin procedure isfull

   if rear equals to MAXSIZE
      return true
   else
      return false
   endif
   
end procedure

Thực hiện hàm isfull () trong ngôn ngữ lập trình C.

Example

bool isfull() {
   if(rear == MAXSIZE - 1)
      return true;
   else
      return false;
}

isempty ()

Thuật toán của hàm isempty () -

Algorithm

begin procedure isempty

   if front is less than MIN  OR front is greater than rear
      return true
   else
      return false
   endif
   
end procedure

Nếu giá trị của front nhỏ hơn MIN hoặc 0, nó cho biết rằng hàng đợi chưa được khởi tạo, do đó trống.

Đây là mã lập trình C -

Example

bool isempty() {
   if(front < 0 || front > rear) 
      return true;
   else
      return false;
}

Hoạt động Enqueue

Hàng đợi duy trì hai con trỏ dữ liệu, front và rear. Do đó, các hoạt động của nó tương đối khó thực hiện hơn so với hoạt động của ngăn xếp.

Các bước sau nên được thực hiện để xếp (chèn) dữ liệu vào hàng đợi:

• Step 1 - Kiểm tra xem hàng đợi đã đầy chưa.

• Step 2 - Nếu hàng đợi đầy, tạo ra lỗi tràn và thoát.

• Step 3 - Nếu hàng đợi không đầy, tăng rear con trỏ để trỏ đến không gian trống tiếp theo.

• Step 4 - Thêm phần tử dữ liệu vào vị trí hàng đợi, nơi mà phía sau đang trỏ tới.

• Step 5 - trả lại thành công.

Đôi khi, chúng tôi cũng kiểm tra xem một hàng đợi có được khởi tạo hay không, để xử lý mọi tình huống không lường trước được.

Thuật toán cho hoạt động hàng đợi

procedure enqueue(data)      
   
   if queue is full
      return overflow
   endif
   
   rear ← rear + 1
   queue[rear] ← data
   return true
   
end procedure

Triển khai enqueue () trong ngôn ngữ lập trình C -

Example

int enqueue(int data)      
   if(isfull())
      return 0;
   
   rear = rear + 1;
   queue[rear] = data;
   
   return 1;
end procedure

Hoạt động Dequeue

Truy cập dữ liệu từ hàng đợi là một quá trình gồm hai tác vụ - truy cập dữ liệu ở đâu frontlà trỏ và xóa dữ liệu sau khi truy cập. Các bước sau được thực hiện để thực hiệndequeue hoạt động -

• Step 1 - Kiểm tra xem hàng đợi có trống không.

• Step 2 - Nếu hàng đợi trống, tạo ra lỗi dòng dưới và thoát.

• Step 3 - Nếu hàng đợi không trống, hãy truy cập dữ liệu ở đâu front đang trỏ.

• Step 4 - Sự gia tăng front con trỏ để trỏ đến phần tử dữ liệu có sẵn tiếp theo.

• Step 5 - Trả lại thành công.

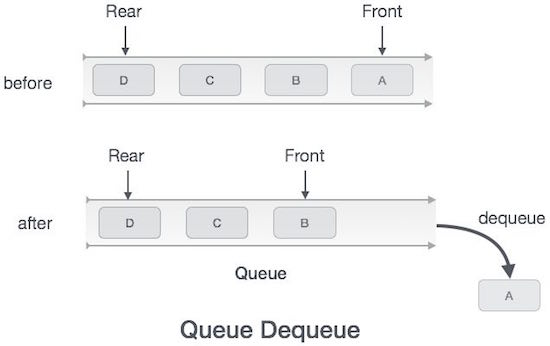
Thuật toán cho hoạt động dequeue

procedure dequeue
   
   if queue is empty
      return underflow
   end if

   data = queue[front]
   front ← front + 1
   return true

end procedure

Thực hiện dequeue () trong ngôn ngữ lập trình C -

Example

int dequeue() {
   if(isempty())
      return 0;

   int data = queue[front];
   front = front + 1;

   return data;
}

Để có chương trình Queue hoàn chỉnh bằng ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Tìm kiếm tuyến tính là một thuật toán tìm kiếm rất đơn giản. Trong kiểu tìm kiếm này, tìm kiếm tuần tự được thực hiện trên tất cả các mục một. Mọi mục đều được kiểm tra và nếu tìm thấy khớp thì mục cụ thể đó sẽ được trả lại, nếu không thì việc tìm kiếm sẽ tiếp tục cho đến khi kết thúc thu thập dữ liệu.

Thuật toán

Linear Search ( Array A, Value x)

Step 1: Set i to 1
Step 2: if i > n then go to step 7
Step 3: if A[i] = x then go to step 6
Step 4: Set i to i + 1
Step 5: Go to Step 2
Step 6: Print Element x Found at index i and go to step 8
Step 7: Print element not found
Step 8: Exit

Mã giả

procedure linear_search (list, value)

   for each item in the list
      if match item == value
         return the item's location
      end if
   end for

end procedure

Để biết về triển khai tìm kiếm tuyến tính trong ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Tìm kiếm nhị phân là một thuật toán tìm kiếm nhanh với độ phức tạp thời gian chạy là Ο (log n). Thuật toán tìm kiếm này hoạt động trên nguyên tắc chia để trị. Để thuật toán này hoạt động bình thường, việc thu thập dữ liệu phải ở dạng được sắp xếp.

Tìm kiếm nhị phân tìm kiếm một mục cụ thể bằng cách so sánh mục giữa hầu hết các bộ sưu tập. Nếu một trận đấu xảy ra, thì chỉ mục của mục sẽ được trả về. Nếu mục ở giữa lớn hơn mục, thì mục được tìm kiếm trong mảng con bên trái của mục giữa. Nếu không, mục được tìm kiếm trong mảng con ở bên phải của mục giữa. Quá trình này cũng tiếp tục trên mảng con cho đến khi kích thước của mảng con giảm xuống 0.

Tìm kiếm nhị phân hoạt động như thế nào?

Để tìm kiếm nhị phân hoạt động, mảng đích phải được sắp xếp. Chúng ta sẽ tìm hiểu quá trình tìm kiếm nhị phân với một ví dụ bằng hình ảnh. Sau đây là mảng được sắp xếp của chúng tôi và giả sử rằng chúng tôi cần tìm kiếm vị trí của giá trị 31 bằng cách sử dụng tìm kiếm nhị phân.

Đầu tiên, chúng ta sẽ xác định một nửa mảng bằng cách sử dụng công thức này:

mid = low + (high - low) / 2

Đây rồi, 0 + (9 - 0) / 2 = 4 (giá trị nguyên của 4,5). Vì vậy, 4 là giữa của mảng.

Bây giờ chúng ta so sánh giá trị được lưu trữ ở vị trí 4, với giá trị đang được tìm kiếm, tức là 31. Chúng tôi thấy rằng giá trị ở vị trí 4 là 27, không phải là một giá trị khớp. Vì giá trị lớn hơn 27 và chúng ta có một mảng đã được sắp xếp, vì vậy chúng ta cũng biết rằng giá trị đích phải nằm ở phần trên của mảng.

Chúng tôi thay đổi mức thấp thành giữa + 1 và tìm lại giá trị giữa mới.

low = mid + 1
mid = low + (high - low) / 2

Mid mới của chúng tôi bây giờ là 7. Chúng tôi so sánh giá trị được lưu trữ tại vị trí 7 với giá trị mục tiêu 31 của chúng tôi.

Giá trị được lưu trữ tại vị trí 7 không phải là một kết quả trùng khớp, đúng hơn là giá trị mà chúng tôi đang tìm kiếm. Vì vậy, giá trị phải ở phần dưới từ vị trí này.

Do đó, chúng tôi tính toán giữa một lần nữa. Lần này là 5.

Chúng tôi so sánh giá trị được lưu trữ tại vị trí 5 với giá trị mục tiêu của chúng tôi. Chúng tôi thấy rằng đó là một trận đấu.

Chúng tôi kết luận rằng giá trị mục tiêu 31 được lưu trữ tại vị trí 5.

Tìm kiếm nhị phân làm giảm một nửa các mục có thể tìm kiếm và do đó làm giảm số lượng so sánh được thực hiện thành các số rất ít.

Mã giả

Mã giả của các thuật toán tìm kiếm nhị phân sẽ trông như thế này:

Procedure binary_search
   A ← sorted array
   n ← size of array
   x ← value to be searched

   Set lowerBound = 1
   Set upperBound = n 

   while x not found
      if upperBound < lowerBound 
         EXIT: x does not exists.
   
      set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
      
      if A[midPoint] < x
         set lowerBound = midPoint + 1
         
      if A[midPoint] > x
         set upperBound = midPoint - 1 

      if A[midPoint] = x 
         EXIT: x found at location midPoint
   end while
   
end procedure

Để biết về cách triển khai tìm kiếm nhị phân sử dụng mảng trong ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Tìm kiếm nội suy là một biến thể cải tiến của tìm kiếm nhị phân. Thuật toán tìm kiếm này hoạt động trên vị trí thăm dò của giá trị được yêu cầu. Để thuật toán này hoạt động bình thường, việc thu thập dữ liệu phải ở dạng được sắp xếp và phân bổ đều.

Tìm kiếm nhị phân có một lợi thế lớn về độ phức tạp về thời gian so với tìm kiếm tuyến tính. Tìm kiếm tuyến tính có độ phức tạp trong trường hợp xấu nhất là Ο (n) trong khi tìm kiếm nhị phân có Ο (log n).

Có những trường hợp có thể biết trước vị trí của dữ liệu đích. Ví dụ, trong trường hợp danh bạ điện thoại, nếu chúng ta muốn tìm kiếm số điện thoại của Morphius. Ở đây, tìm kiếm tuyến tính và thậm chí tìm kiếm nhị phân sẽ có vẻ chậm vì chúng ta có thể chuyển trực tiếp đến không gian bộ nhớ nơi các tên bắt đầu từ 'M' được lưu trữ.

Định vị trong Tìm kiếm nhị phân

Trong tìm kiếm nhị phân, nếu dữ liệu mong muốn không được tìm thấy thì phần còn lại của danh sách được chia thành hai phần, thấp hơn và cao hơn. Việc tìm kiếm được thực hiện ở một trong hai.

Ngay cả khi dữ liệu được sắp xếp, tìm kiếm nhị phân không tận dụng để thăm dò vị trí của dữ liệu mong muốn.

Thăm dò vị trí trong tìm kiếm nội suy

Tìm kiếm nội suy tìm một mục cụ thể bằng cách tính toán vị trí đầu dò. Ban đầu, vị trí đầu dò là vị trí của vật phẩm chính giữa nhất của bộ sưu tập.

Nếu một sự trùng khớp xảy ra, thì chỉ mục của mục sẽ được trả về. Để chia danh sách thành hai phần, chúng tôi sử dụng phương pháp sau:

mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])

where −
   A    = list
   Lo   = Lowest index of the list
   Hi   = Highest index of the list
   A[n] = Value stored at index n in the list

Nếu mục ở giữa lớn hơn mục, thì vị trí thăm dò lại được tính trong mảng con bên phải của mục giữa. Nếu không, mục sẽ được tìm kiếm trong mảng con bên trái của mục giữa. Quá trình này cũng tiếp tục trên mảng con cho đến khi kích thước của mảng con giảm xuống 0.

Độ phức tạp thời gian chạy của thuật toán tìm kiếm nội suy là Ο(log (log n)) so với Ο(log n) của BST trong những tình huống thuận lợi.

Thuật toán

Vì đây là sự ứng biến của thuật toán BST hiện có, chúng tôi đang đề cập đến các bước để tìm kiếm chỉ mục giá trị dữ liệu 'mục tiêu', sử dụng thăm dò vị trí -

Step 1 − Start searching data from middle of the list.
Step 2 − If it is a match, return the index of the item, and exit.
Step 3 − If it is not a match, probe position.
Step 4 − Divide the list using probing formula and find the new midle.
Step 5 − If data is greater than middle, search in higher sub-list.
Step 6 − If data is smaller than middle, search in lower sub-list.
Step 7 − Repeat until match.

Mã giả

A → Array list
N → Size of A
X → Target Value

Procedure Interpolation_Search()

   Set Lo  →  0
   Set Mid → -1
   Set Hi  →  N-1

   While X does not match
   
      if Lo equals to Hi OR A[Lo] equals to A[Hi]
         EXIT: Failure, Target not found
      end if
      
      Set Mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo]) 

      if A[Mid] = X
         EXIT: Success, Target found at Mid
      else 
         if A[Mid] < X
            Set Lo to Mid+1
         else if A[Mid] > X
            Set Hi to Mid-1
         end if
      end if
   End While

End Procedure

Để biết về việc thực hiện tìm kiếm nội suy trong ngôn ngữ lập trình C, hãy nhấp vào đây .

Bảng băm là một cấu trúc dữ liệu lưu trữ dữ liệu theo cách liên kết. Trong bảng băm, dữ liệu được lưu trữ ở định dạng mảng, trong đó mỗi giá trị dữ liệu có giá trị chỉ mục duy nhất của riêng nó. Việc truy cập dữ liệu trở nên rất nhanh nếu chúng ta biết chỉ mục của dữ liệu mong muốn.

Do đó, nó trở thành một cấu trúc dữ liệu trong đó các thao tác chèn và tìm kiếm rất nhanh chóng bất kể kích thước của dữ liệu. Bảng băm sử dụng một mảng làm phương tiện lưu trữ và sử dụng kỹ thuật băm để tạo chỉ mục nơi một phần tử sẽ được chèn vào hoặc được định vị từ đó.

Băm

Hashing là một kỹ thuật để chuyển đổi một loạt các giá trị khóa thành một loạt các chỉ mục của một mảng. Chúng ta sẽ sử dụng toán tử modulo để nhận một loạt các giá trị chính. Hãy xem xét một ví dụ về bảng băm có kích thước 20 và các mục sau đây sẽ được lưu trữ. Mục ở định dạng (khóa, giá trị).

• (1,20)
• (2,70)
• (42,80)
• (4,25)
• (12,44)
• (14,32)
• (17,11)
• (13,78)
• (37,98)

Sr.No.	Chìa khóa	Băm	Chỉ mục mảng
1	1	1% 20 = 1	1
2	2	2% 20 = 2	2
3	42	42% 20 = 2	2
4	4	4% 20 = 4	4
5	12	12% 20 = 12	12
6	14	14% 20 = 14	14
7	17	17% 20 = 17	17
số 8	13	13% 20 = 13	13
9	37	37% 20 = 17	17

Đo tuyến tính

Như chúng ta thấy, có thể xảy ra trường hợp kỹ thuật băm được sử dụng để tạo chỉ mục đã được sử dụng của mảng. Trong trường hợp như vậy, chúng ta có thể tìm kiếm vị trí trống tiếp theo trong mảng bằng cách nhìn vào ô tiếp theo cho đến khi tìm thấy ô trống. Kỹ thuật này được gọi là thăm dò tuyến tính.

Sr.No.	Chìa khóa	Băm	Chỉ mục mảng	Sau khi dò tuyến tính, chỉ mục mảng
1	1	1% 20 = 1	1	1
2	2	2% 20 = 2	2	2
3	42	42% 20 = 2	2	3
4	4	4% 20 = 4	4	4
5	12	12% 20 = 12	12	12
6	14	14% 20 = 14	14	14
7	17	17% 20 = 17	17	17
số 8	13	13% 20 = 13	13	13
9	37	37% 20 = 17	17	18

Hoạt động cơ bản

Sau đây là các hoạt động chính cơ bản của bảng băm.

• Search - Tìm kiếm một phần tử trong bảng băm.

• Insert - Chèn một phần tử trong bảng băm.

• delete - Xóa một phần tử khỏi bảng băm.

Mục dữ liệu

Xác định một mục dữ liệu có một số dữ liệu và khóa, dựa trên đó việc tìm kiếm sẽ được thực hiện trong bảng băm.

struct DataItem {
   int data;
   int key;
};

Phương pháp băm

Xác định phương pháp băm để tính mã băm của khóa của mục dữ liệu.

int hashCode(int key){
   return key % SIZE;
}

Hoạt động tìm kiếm

Bất cứ khi nào một phần tử được tìm kiếm, hãy tính toán mã băm của khóa được truyền và xác định vị trí phần tử bằng cách sử dụng mã băm đó làm chỉ mục trong mảng. Sử dụng thăm dò tuyến tính để đưa phần tử đi trước nếu phần tử không được tìm thấy trong mã băm đã tính.

Thí dụ

struct DataItem *search(int key) {
   //get the hash
   int hashIndex = hashCode(key);
	
   //move in array until an empty
   while(hashArray[hashIndex] != NULL) {
	
      if(hashArray[hashIndex]->key == key)
         return hashArray[hashIndex];
			
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }

   return NULL;        
}

Chèn hoạt động

Bất cứ khi nào một phần tử được chèn vào, hãy tính mã băm của khóa được truyền và xác định vị trí chỉ mục bằng cách sử dụng mã băm đó làm chỉ mục trong mảng. Sử dụng thăm dò tuyến tính cho vị trí trống, nếu một phần tử được tìm thấy trong mã băm được tính toán.

Thí dụ

void insert(int key,int data) {
   struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
   item->data = data;  
   item->key = key;     

   //get the hash 
   int hashIndex = hashCode(key);

   //move in array until an empty or deleted cell
   while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) {
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }
	
   hashArray[hashIndex] = item;        
}

Xóa hoạt động

Bất cứ khi nào một phần tử bị xóa, hãy tính toán mã băm của khóa được truyền và xác định chỉ mục bằng cách sử dụng mã băm đó làm chỉ mục trong mảng. Sử dụng thăm dò tuyến tính để đưa phần tử đi trước nếu phần tử không được tìm thấy trong mã băm đã tính. Khi tìm thấy, hãy lưu trữ một vật phẩm giả ở đó để giữ nguyên hiệu suất của bảng băm.

Thí dụ

struct DataItem* delete(struct DataItem* item) {
   int key = item->key;

   //get the hash 
   int hashIndex = hashCode(key);

   //move in array until an empty 
   while(hashArray[hashIndex] !=NULL) {
	
      if(hashArray[hashIndex]->key == key) {
         struct DataItem* temp = hashArray[hashIndex]; 
			
         //assign a dummy item at deleted position
         hashArray[hashIndex] = dummyItem; 
         return temp;
      } 
		
      //go to next cell
      ++hashIndex;
		
      //wrap around the table
      hashIndex %= SIZE;
   }  
	
   return NULL;        
}

Để biết về triển khai băm trong ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Sắp xếp đề cập đến việc sắp xếp dữ liệu theo một định dạng cụ thể. Thuật toán sắp xếp chỉ định cách sắp xếp dữ liệu theo một thứ tự cụ thể. Hầu hết các đơn đặt hàng phổ biến theo thứ tự số hoặc từ điển.

Tầm quan trọng của việc sắp xếp nằm ở chỗ, việc tìm kiếm dữ liệu có thể được tối ưu hóa ở mức rất cao, nếu dữ liệu được lưu trữ theo cách được sắp xếp. Sắp xếp cũng được sử dụng để biểu diễn dữ liệu ở các định dạng dễ đọc hơn. Sau đây là một số ví dụ về sắp xếp trong các tình huống thực tế -

• Telephone Directory - Danh bạ điện thoại lưu trữ số điện thoại của những người được sắp xếp theo tên của họ, để có thể tra cứu tên dễ dàng.

• Dictionary - Từ điển lưu trữ các từ theo thứ tự bảng chữ cái để việc tìm kiếm bất kỳ từ nào trở nên dễ dàng.

Sắp xếp tại chỗ và Sắp xếp không tại chỗ

Các thuật toán sắp xếp có thể yêu cầu thêm một số không gian để so sánh và lưu trữ tạm thời một số phần tử dữ liệu. Các thuật toán này không yêu cầu thêm bất kỳ không gian nào và việc sắp xếp được cho là diễn ra tại chỗ, hoặc ví dụ, trong chính mảng. Đây được gọi làin-place sorting. Sắp xếp bong bóng là một ví dụ về sắp xếp tại chỗ.

Tuy nhiên, trong một số thuật toán sắp xếp, chương trình yêu cầu không gian lớn hơn hoặc bằng các phần tử được sắp xếp. Sắp xếp sử dụng không gian bằng hoặc nhiều hơn được gọi lànot-in-place sorting. Merge-sort là một ví dụ về sắp xếp không đúng vị trí.

Sắp xếp ổn định và không ổn định

Nếu một thuật toán sắp xếp, sau khi sắp xếp nội dung, không thay đổi chuỗi nội dung tương tự mà chúng xuất hiện, nó được gọi là stable sorting.

Nếu một thuật toán sắp xếp, sau khi sắp xếp nội dung, thay đổi trình tự của nội dung tương tự mà chúng xuất hiện, nó được gọi là unstable sorting.

Tính ổn định của một thuật toán quan trọng khi chúng ta muốn duy trì chuỗi các phần tử ban đầu, chẳng hạn như trong một bộ tuple.

Thuật toán sắp xếp thích ứng và không thích ứng

Thuật toán sắp xếp được cho là thích ứng, nếu nó tận dụng các phần tử đã được 'sắp xếp' trong danh sách được sắp xếp. Nghĩa là, trong khi sắp xếp nếu danh sách nguồn có một số phần tử đã được sắp xếp, các thuật toán thích ứng sẽ tính đến điều này và sẽ cố gắng không sắp xếp lại chúng.

Thuật toán không thích ứng là thuật toán không tính đến các phần tử đã được sắp xếp. Họ cố gắng buộc mọi phần tử được sắp xếp lại để xác nhận tính sắp xếp của chúng.

Điều khoản quan trọng

Một số thuật ngữ thường được đặt ra trong khi thảo luận về các kỹ thuật sắp xếp, đây là phần giới thiệu ngắn gọn về chúng -

Tăng cao sự đặt hàng

Một chuỗi các giá trị được cho là trong increasing order, nếu phần tử kế tiếp lớn hơn phần tử trước. Ví dụ: 1, 3, 4, 6, 8, 9 theo thứ tự tăng dần, vì mọi phần tử tiếp theo đều lớn hơn phần tử trước.

Lệnh giảm

Một chuỗi các giá trị được cho là trong decreasing order, nếu phần tử kế tiếp nhỏ hơn phần tử hiện tại. Ví dụ: 9, 8, 6, 4, 3, 1 theo thứ tự giảm dần, vì mọi phần tử tiếp theo đều nhỏ hơn phần tử trước.

Đơn hàng không tăng

Một chuỗi các giá trị được cho là trong non-increasing order, nếu phần tử kế tiếp nhỏ hơn hoặc bằng phần tử trước của nó trong dãy. Thứ tự này xảy ra khi chuỗi chứa các giá trị trùng lặp. Ví dụ: 9, 8, 6, 3, 3, 1 theo thứ tự không tăng, vì mọi phần tử tiếp theo đều nhỏ hơn hoặc bằng (trong trường hợp 3) nhưng không lớn hơn bất kỳ phần tử nào trước đó.

Thứ tự không giảm

Một chuỗi các giá trị được cho là trong non-decreasing order, nếu phần tử kế tiếp lớn hơn hoặc bằng phần tử trước đó của nó trong dãy. Thứ tự này xảy ra khi chuỗi chứa các giá trị trùng lặp. Ví dụ: 1, 3, 3, 6, 8, 9 theo thứ tự không giảm, vì mọi phần tử tiếp theo đều lớn hơn hoặc bằng (trong trường hợp 3) nhưng không nhỏ hơn phần tử trước.

Sắp xếp bong bóng là một thuật toán sắp xếp đơn giản. Thuật toán sắp xếp này là thuật toán dựa trên so sánh trong đó từng cặp phần tử liền kề được so sánh và các phần tử được hoán đổi nếu chúng không theo thứ tự. Thuật toán này không phù hợp với các tập dữ liệu lớn vì độ phức tạp trung bình và trường hợp xấu nhất của nó là Ο (n ² ) trong đón là số lượng mặt hàng.

Cách sắp xếp bong bóng hoạt động?

Chúng tôi lấy một mảng không được sắp xếp để làm ví dụ. Sắp xếp bong bóng mất Ο (n ² ) thời gian nên chúng tôi đang giữ cho nó ngắn gọn và chính xác.

Sắp xếp bong bóng bắt đầu với hai phần tử đầu tiên, so sánh chúng để kiểm tra xem cái nào lớn hơn.

Trong trường hợp này, giá trị 33 lớn hơn 14, vì vậy nó đã nằm trong các vị trí được sắp xếp. Tiếp theo, chúng tôi so sánh 33 với 27.

Chúng tôi thấy rằng 27 nhỏ hơn 33 và hai giá trị này phải được đổi chỗ cho nhau.

Mảng mới sẽ trông như thế này -

Tiếp theo, chúng tôi so sánh 33 và 35. Chúng tôi thấy rằng cả hai đều ở các vị trí đã được sắp xếp.

Sau đó, chúng tôi chuyển sang hai giá trị tiếp theo, 35 và 10.

Khi đó chúng ta biết rằng 10 nhỏ hơn 35. Do đó chúng không được sắp xếp.

Chúng tôi hoán đổi các giá trị này. Chúng tôi thấy rằng chúng tôi đã đến cuối mảng. Sau một lần lặp, mảng sẽ trông như thế này:

Nói một cách chính xác, chúng ta đang chỉ ra một mảng trông như thế nào sau mỗi lần lặp. Sau lần lặp thứ hai, nó sẽ trông như thế này -

Lưu ý rằng sau mỗi lần lặp, có ít nhất một giá trị di chuyển ở cuối.

Và khi không yêu cầu hoán đổi, sắp xếp bong bóng biết rằng một mảng được sắp xếp hoàn toàn.

Bây giờ chúng ta nên xem xét một số khía cạnh thực tế của phân loại bong bóng.

Thuật toán

Chúng tôi giả định list là một mảng của ncác yếu tố. Chúng tôi cũng giả định rằngswap hàm hoán đổi giá trị của các phần tử mảng đã cho.

begin BubbleSort(list)

   for all elements of list
      if list[i] > list[i+1]
         swap(list[i], list[i+1])
      end if
   end for
   
   return list
   
end BubbleSort

Mã giả

Chúng tôi quan sát thấy trong thuật toán Bubble Sort so sánh từng cặp phần tử của mảng trừ khi toàn bộ mảng được sắp xếp hoàn toàn theo thứ tự tăng dần. Điều này có thể gây ra một số vấn đề phức tạp như điều gì xảy ra nếu mảng không cần hoán đổi nữa vì tất cả các phần tử đã tăng dần.

Để giải quyết vấn đề, chúng tôi sử dụng một biến cờ swappedđiều này sẽ giúp chúng tôi xem liệu có bất kỳ sự hoán đổi nào đã xảy ra hay không. Nếu không có hoán đổi nào xảy ra, tức là mảng không yêu cầu xử lý nữa để được sắp xếp, nó sẽ thoát ra khỏi vòng lặp.

Mã giả của thuật toán BubbleSort có thể được viết như sau:

procedure bubbleSort( list : array of items )

   loop = list.count;
   
   for i = 0 to loop-1 do:
      swapped = false
		
      for j = 0 to loop-1 do:
      
         /* compare the adjacent elements */   
         if list[j] > list[j+1] then
            /* swap them */
            swap( list[j], list[j+1] )		 
            swapped = true
         end if
         
      end for
      
      /*if no number was swapped that means 
      array is sorted now, break the loop.*/
      
      if(not swapped) then
         break
      end if
      
   end for
   
end procedure return list

Thực hiện

Một vấn đề nữa mà chúng tôi đã không giải quyết trong thuật toán ban đầu và mã giả ứng biến của nó, đó là, sau mỗi lần lặp, các giá trị cao nhất sẽ lắng xuống ở cuối mảng. Do đó, lần lặp tiếp theo không cần bao gồm các phần tử đã được sắp xếp. Vì mục đích này, khi triển khai, chúng tôi hạn chế vòng lặp bên trong để tránh các giá trị đã được sắp xếp.

Để biết về cách triển khai sắp xếp bong bóng trong ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Đây là một thuật toán sắp xếp dựa trên so sánh tại chỗ. Ở đây, một danh sách phụ được duy trì và luôn được sắp xếp. Ví dụ, phần dưới của một mảng được duy trì để được sắp xếp. Một phần tử sẽ được 'chèn' vào danh sách con được sắp xếp này, phải tìm vị trí thích hợp của nó và sau đó nó phải được chèn vào đó. Do đó tên,insertion sort.

Mảng được tìm kiếm tuần tự và các mục không được sắp xếp được di chuyển và chèn vào danh sách con đã sắp xếp (trong cùng một mảng). Thuật toán này không phù hợp với các tập dữ liệu lớn vì độ phức tạp trung bình và trường hợp xấu nhất của nó là Ο (n ² ), trong đón là số lượng mặt hàng.

Cách sắp xếp chèn hoạt động?

Chúng tôi lấy một mảng không được sắp xếp để làm ví dụ.

Sắp xếp chèn so sánh hai phần tử đầu tiên.

Nó phát hiện ra rằng cả 14 và 33 đã theo thứ tự tăng dần. Hiện tại, 14 nằm trong danh sách phụ được sắp xếp.

Sắp xếp chèn di chuyển lên phía trước và so sánh 33 với 27.

Và thấy rằng 33 không ở đúng vị trí.

Nó hoán đổi 33 với 27. Nó cũng kiểm tra với tất cả các phần tử của danh sách con được sắp xếp. Ở đây chúng ta thấy rằng danh sách con đã sắp xếp chỉ có một phần tử 14 và 27 lớn hơn 14. Do đó, danh sách con đã sắp xếp vẫn được sắp xếp sau khi hoán đổi.

Bây giờ chúng ta có 14 và 27 trong danh sách phụ đã sắp xếp. Tiếp theo, nó so sánh 33 với 10.

Các giá trị này không theo thứ tự được sắp xếp.

Vì vậy, chúng tôi hoán đổi chúng.

Tuy nhiên, việc hoán đổi làm cho 27 và 10 không được sắp xếp.

Do đó, chúng tôi cũng hoán đổi chúng.

Một lần nữa, chúng tôi tìm thấy 14 và 10 theo một thứ tự không được sắp xếp.

Chúng tôi hoán đổi chúng một lần nữa. Đến cuối lần lặp thứ ba, chúng ta có một danh sách phụ được sắp xếp gồm 4 mục.

Quá trình này tiếp tục cho đến khi tất cả các giá trị chưa được sắp xếp được bao phủ trong một danh sách con được sắp xếp. Bây giờ chúng ta sẽ thấy một số khía cạnh lập trình của sắp xếp chèn.

Thuật toán

Bây giờ chúng ta có một bức tranh toàn cảnh hơn về cách hoạt động của kỹ thuật sắp xếp này, vì vậy chúng ta có thể rút ra các bước đơn giản mà chúng ta có thể đạt được sắp xếp chèn.

Step 1 − If it is the first element, it is already sorted. return 1;
Step 2 − Pick next element
Step 3 − Compare with all elements in the sorted sub-list
Step 4 − Shift all the elements in the sorted sub-list that is greater than the 
         value to be sorted
Step 5 − Insert the value
Step 6 − Repeat until list is sorted

Mã giả

procedure insertionSort( A : array of items )
   int holePosition
   int valueToInsert
	
   for i = 1 to length(A) inclusive do:
	
      /* select value to be inserted */
      valueToInsert = A[i]
      holePosition = i
      
      /*locate hole position for the element to be inserted */
		
      while holePosition > 0 and A[holePosition-1] > valueToInsert do:
         A[holePosition] = A[holePosition-1]
         holePosition = holePosition -1
      end while
		
      /* insert the number at hole position */
      A[holePosition] = valueToInsert
      
   end for
	
end procedure

Để biết về cách triển khai sắp xếp chèn trong ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Sắp xếp lựa chọn là một thuật toán sắp xếp đơn giản. Thuật toán sắp xếp này là một thuật toán dựa trên so sánh tại chỗ trong đó danh sách được chia thành hai phần, phần được sắp xếp ở đầu bên trái và phần chưa được sắp xếp ở đầu bên phải. Ban đầu, phần được sắp xếp trống và phần không được sắp xếp là toàn bộ danh sách.

Phần tử nhỏ nhất được chọn từ mảng chưa được sắp xếp và đổi chỗ với phần tử ngoài cùng bên trái và phần tử đó trở thành một phần của mảng đã sắp xếp. Quá trình này tiếp tục di chuyển ranh giới mảng chưa được sắp xếp theo một phần tử sang bên phải.

Thuật toán này không phù hợp với các tập dữ liệu lớn vì độ phức tạp trung bình và trường hợp xấu nhất của nó là Ο (n ² ), trong đón là số lượng mặt hàng.

Cách sắp xếp lựa chọn hoạt động?

Hãy xem xét mảng được mô tả sau đây làm ví dụ.

Đối với vị trí đầu tiên trong danh sách đã sắp xếp, toàn bộ danh sách được quét tuần tự. Vị trí đầu tiên mà 14 được lưu trữ hiện tại, chúng tôi tìm kiếm toàn bộ danh sách và thấy rằng 10 là giá trị thấp nhất.

Vì vậy, chúng tôi thay thế 14 bằng 10. Sau một lần lặp lại 10, giá trị này xảy ra là giá trị nhỏ nhất trong danh sách, xuất hiện ở vị trí đầu tiên của danh sách đã sắp xếp.

Đối với vị trí thứ hai, nơi có 33, chúng tôi bắt đầu quét phần còn lại của danh sách theo cách tuyến tính.

Chúng tôi thấy rằng 14 là giá trị thấp thứ hai trong danh sách và nó sẽ xuất hiện ở vị trí thứ hai. Chúng tôi hoán đổi các giá trị này.

Sau hai lần lặp, hai giá trị nhỏ nhất được định vị ở đầu theo cách được sắp xếp.

Quy trình tương tự được áp dụng cho phần còn lại của các mục trong mảng.

Sau đây là hình ảnh mô tả toàn bộ quá trình phân loại -

Bây giờ, chúng ta hãy tìm hiểu một số khía cạnh lập trình của sắp xếp lựa chọn.

Thuật toán

Step 1 − Set MIN to location 0
Step 2 − Search the minimum element in the list
Step 3 − Swap with value at location MIN
Step 4 − Increment MIN to point to next element
Step 5 − Repeat until list is sorted

Mã giả

procedure selection sort 
   list  : array of items
   n     : size of list

   for i = 1 to n - 1
   /* set current element as minimum*/
      min = i    
  
      /* check the element to be minimum */

      for j = i+1 to n 
         if list[j] < list[min] then
            min = j;
         end if
      end for

      /* swap the minimum element with the current element*/
      if indexMin != i  then
         swap list[min] and list[i]
      end if
   end for
	
end procedure

Để biết về triển khai sắp xếp lựa chọn trong ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Merge sort là một kỹ thuật sắp xếp dựa trên kỹ thuật chia để trị. Với độ phức tạp thời gian trong trường hợp xấu nhất là Ο (n log n), nó là một trong những thuật toán được đánh giá cao nhất.

Merge sort đầu tiên chia mảng thành các nửa bằng nhau và sau đó kết hợp chúng theo cách đã sắp xếp.

Cách Merge Sort hoạt động?

Để hiểu sắp xếp hợp nhất, chúng tôi lấy một mảng không được sắp xếp như sau:

Chúng ta biết rằng sắp xếp hợp nhất chia lặp đi lặp lại toàn bộ mảng thành các nửa bằng nhau trừ khi đạt được các giá trị nguyên tử. Ở đây chúng ta thấy rằng một mảng 8 mục được chia thành hai mảng có kích thước 4.

Điều này không thay đổi trình tự xuất hiện của các mục trong bản gốc. Bây giờ chúng ta chia hai mảng này thành một nửa.

Chúng tôi tiếp tục chia các mảng này và chúng tôi đạt được giá trị nguyên tử mà không thể chia được nữa.

Bây giờ, chúng tôi kết hợp chúng theo cách giống hệt như khi chúng được chia nhỏ. Xin lưu ý các mã màu được cung cấp cho các danh sách này.

Trước tiên, chúng tôi so sánh phần tử cho từng danh sách và sau đó kết hợp chúng thành một danh sách khác theo cách được sắp xếp. Chúng ta thấy rằng 14 và 33 ở các vị trí đã được sắp xếp. Chúng tôi so sánh 27 và 10 và trong danh sách mục tiêu có 2 giá trị, chúng tôi đặt 10 đầu tiên, tiếp theo là 27. Chúng tôi thay đổi thứ tự của 19 và 35 trong khi 42 và 44 được đặt tuần tự.

Trong lần lặp tiếp theo của giai đoạn kết hợp, chúng tôi so sánh danh sách của hai giá trị dữ liệu và hợp nhất chúng thành danh sách các giá trị dữ liệu tìm thấy, đặt tất cả theo thứ tự đã sắp xếp.

Sau lần hợp nhất cuối cùng, danh sách sẽ như thế này -

Bây giờ chúng ta nên tìm hiểu một số khía cạnh lập trình của sắp xếp hợp nhất.

Thuật toán

Sắp xếp hợp nhất tiếp tục chia danh sách thành các nửa bằng nhau cho đến khi không thể chia được nữa. Theo định nghĩa, nếu nó chỉ là một phần tử trong danh sách, nó sẽ được sắp xếp. Sau đó, sắp xếp hợp nhất kết hợp các danh sách được sắp xếp nhỏ hơn giữ cho danh sách mới cũng được sắp xếp.

Step 1 − if it is only one element in the list it is already sorted, return.
Step 2 − divide the list recursively into two halves until it can no more be divided.
Step 3 − merge the smaller lists into new list in sorted order.

Mã giả

Bây giờ chúng ta sẽ thấy các mã giả cho các hàm sắp xếp hợp nhất. Như các thuật toán của chúng tôi chỉ ra hai chức năng chính - phân chia và hợp nhất.

Merge sort hoạt động với đệ quy và chúng ta sẽ thấy việc triển khai của chúng ta theo cùng một cách.

procedure mergesort( var a as array )
   if ( n == 1 ) return a

   var l1 as array = a[0] ... a[n/2]
   var l2 as array = a[n/2+1] ... a[n]

   l1 = mergesort( l1 )
   l2 = mergesort( l2 )

   return merge( l1, l2 )
end procedure

procedure merge( var a as array, var b as array )

   var c as array
   while ( a and b have elements )
      if ( a[0] > b[0] )
         add b[0] to the end of c
         remove b[0] from b
      else
         add a[0] to the end of c
         remove a[0] from a
      end if
   end while
   
   while ( a has elements )
      add a[0] to the end of c
      remove a[0] from a
   end while
   
   while ( b has elements )
      add b[0] to the end of c
      remove b[0] from b
   end while
   
   return c
	
end procedure

Để biết về triển khai sắp xếp hợp nhất trong ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Shell sort là một thuật toán sắp xếp hiệu quả cao và dựa trên thuật toán sắp xếp chèn. Thuật toán này tránh sự thay đổi lớn như trong trường hợp sắp xếp chèn, nếu giá trị nhỏ hơn ở ngoài cùng bên phải và phải được di chuyển sang ngoài cùng bên trái.

Thuật toán này sử dụng sắp xếp chèn trên các phần tử phổ biến rộng rãi, trước tiên để sắp xếp chúng và sau đó sắp xếp các phần tử có khoảng cách ít hơn. Khoảng cách này được gọi làinterval. Khoảng thời gian này được tính dựa trên công thức của Knuth là:

Công thức Knuth

h = h * 3 + 1
where −
   h is interval with initial value 1

Thuật toán này khá hiệu quả đối với các tập dữ liệu cỡ vừa vì độ phức tạp trung bình và trường hợp xấu nhất của nó là Ο (n), trong đó n là số lượng mặt hàng.

Shell Sort hoạt động như thế nào?

Chúng ta hãy xem xét ví dụ sau để có ý tưởng về cách hoạt động của shell sort. Chúng tôi lấy cùng một mảng mà chúng tôi đã sử dụng trong các ví dụ trước của chúng tôi. Để làm ví dụ và dễ hiểu, chúng ta lấy khoảng 4. Tạo một danh sách con ảo gồm tất cả các giá trị nằm trong khoảng 4 vị trí. Ở đây các giá trị này là {35, 14}, {33, 19}, {42, 27} và {10, 44}

Chúng tôi so sánh các giá trị trong mỗi danh sách con và hoán đổi chúng (nếu cần) trong mảng ban đầu. Sau bước này, mảng mới sẽ giống như sau:

Sau đó, chúng tôi lấy khoảng 2 và khoảng cách này tạo ra hai danh sách con - {14, 27, 35, 42}, {19, 10, 33, 44}

Chúng tôi so sánh và hoán đổi các giá trị, nếu cần, trong mảng ban đầu. Sau bước này, mảng sẽ trông như thế này:

Cuối cùng, chúng tôi sắp xếp phần còn lại của mảng bằng cách sử dụng khoảng giá trị 1. Shell sắp xếp sử dụng sắp xếp chèn để sắp xếp mảng.

Sau đây là mô tả từng bước -

Chúng ta thấy rằng chỉ cần bốn lần hoán đổi để sắp xếp phần còn lại của mảng.

Thuật toán

Sau đây là thuật toán sắp xếp trình bao.

Step 1 − Initialize the value of h
Step 2 − Divide the list into smaller sub-list of equal interval h
Step 3 − Sort these sub-lists using insertion sort
Step 3 − Repeat until complete list is sorted

Mã giả

Sau đây là mã giả cho phân loại shell.

procedure shellSort()
   A : array of items 
	
   /* calculate interval*/
   while interval < A.length /3 do:
      interval = interval * 3 + 1	    
   end while
   
   while interval > 0 do:

      for outer = interval; outer < A.length; outer ++ do:

      /* select value to be inserted */
      valueToInsert = A[outer]
      inner = outer;

         /*shift element towards right*/
         while inner > interval -1 && A[inner - interval] >= valueToInsert do:
            A[inner] = A[inner - interval]
            inner = inner - interval
         end while

      /* insert the number at hole position */
      A[inner] = valueToInsert

      end for

   /* calculate interval*/
   interval = (interval -1) /3;	  

   end while
   
end procedure

Để biết về cách triển khai shell sort trong ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Shell sort là một thuật toán sắp xếp hiệu quả cao và dựa trên thuật toán sắp xếp chèn. Thuật toán này tránh sự thay đổi lớn như trong trường hợp sắp xếp chèn, nếu giá trị nhỏ hơn ở ngoài cùng bên phải và phải được di chuyển sang ngoài cùng bên trái.

Thuật toán này sử dụng sắp xếp chèn trên các phần tử phổ biến rộng rãi, trước tiên để sắp xếp chúng và sau đó sắp xếp các phần tử có khoảng cách ít hơn. Khoảng cách này được gọi làinterval. Khoảng thời gian này được tính dựa trên công thức của Knuth là:

Công thức Knuth

h = h * 3 + 1
where −
   h is interval with initial value 1

Thuật toán này khá hiệu quả đối với các tập dữ liệu cỡ trung bình vì độ phức tạp trung bình và trường hợp xấu nhất của thuật toán này phụ thuộc vào chuỗi khoảng trống được biết đến nhiều nhất là Ο (n), trong đó n là số mục. Và độ phức tạp không gian trong trường hợp xấu nhất là O (n).

Shell Sort hoạt động như thế nào?

Chúng ta hãy xem xét ví dụ sau để có ý tưởng về cách hoạt động của shell sort. Chúng tôi lấy cùng một mảng mà chúng tôi đã sử dụng trong các ví dụ trước của chúng tôi. Để làm ví dụ và dễ hiểu, chúng ta lấy khoảng 4. Tạo một danh sách con ảo gồm tất cả các giá trị nằm trong khoảng 4 vị trí. Ở đây các giá trị này là {35, 14}, {33, 19}, {42, 27} và {10, 44}

Chúng tôi so sánh các giá trị trong mỗi danh sách con và hoán đổi chúng (nếu cần) trong mảng ban đầu. Sau bước này, mảng mới sẽ giống như sau:

Sau đó, chúng tôi lấy khoảng 1 và khoảng cách này tạo ra hai danh sách con - {14, 27, 35, 42}, {19, 10, 33, 44}

Chúng tôi so sánh và hoán đổi các giá trị, nếu cần, trong mảng ban đầu. Sau bước này, mảng sẽ trông như thế này:

Cuối cùng, chúng tôi sắp xếp phần còn lại của mảng bằng cách sử dụng khoảng giá trị 1. Shell sắp xếp sử dụng sắp xếp chèn để sắp xếp mảng.

Sau đây là mô tả từng bước -

Chúng ta thấy rằng chỉ cần bốn lần hoán đổi để sắp xếp phần còn lại của mảng.

Thuật toán

Sau đây là thuật toán sắp xếp trình bao.

Step 1 − Initialize the value of h
Step 2 − Divide the list into smaller sub-list of equal interval h
Step 3 − Sort these sub-lists using insertion sort
Step 3 − Repeat until complete list is sorted

Mã giả

Sau đây là mã giả cho phân loại shell.

procedure shellSort()
   A : array of items 
	
   /* calculate interval*/
   while interval < A.length /3 do:
      interval = interval * 3 + 1	    
   end while
   
   while interval > 0 do:

      for outer = interval; outer < A.length; outer ++ do:

      /* select value to be inserted */
      valueToInsert = A[outer]
      inner = outer;

         /*shift element towards right*/
         while inner > interval -1 && A[inner - interval] >= valueToInsert do:
            A[inner] = A[inner - interval]
            inner = inner - interval
         end while

      /* insert the number at hole position */
      A[inner] = valueToInsert

      end for

   /* calculate interval*/
   interval = (interval -1) /3;	  

   end while
   
end procedure

Để biết về cách triển khai shell sort trong ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Sắp xếp nhanh là một thuật toán sắp xếp hiệu quả cao và dựa trên việc phân chia mảng dữ liệu thành các mảng nhỏ hơn. Một mảng lớn được phân vùng thành hai mảng, một mảng chứa các giá trị nhỏ hơn giá trị được chỉ định, chẳng hạn như pivot, dựa vào đó phân vùng được tạo và một mảng khác giữ các giá trị lớn hơn giá trị pivot.

Quicksort phân vùng một mảng và sau đó gọi chính nó đệ quy hai lần để sắp xếp hai mảng con kết quả. Thuật toán này khá hiệu quả đối với các tập dữ liệu có kích thước lớn vì độ phức tạp trung bình và trường hợp xấu nhất của nó lần lượt là O (nLogn) và image.png (n ² ).

Phân vùng trong Sắp xếp nhanh

Sau đây biểu diễn động giải thích cách tìm giá trị tổng hợp trong một mảng.

Giá trị pivot chia danh sách thành hai phần. Và đệ quy, chúng tôi tìm tổng hợp cho mỗi danh sách con cho đến khi tất cả các danh sách chỉ chứa một phần tử.

Thuật toán Pivot Sắp xếp Nhanh

Dựa trên hiểu biết của chúng tôi về phân vùng theo kiểu sắp xếp nhanh, bây giờ chúng tôi sẽ cố gắng viết một thuật toán cho nó, như sau.

Step 1 − Choose the highest index value has pivot
Step 2 − Take two variables to point left and right of the list excluding pivot
Step 3 − left points to the low index
Step 4 − right points to the high
Step 5 − while value at left is less than pivot move right
Step 6 − while value at right is greater than pivot move left
Step 7 − if both step 5 and step 6 does not match swap left and right
Step 8 − if left ≥ right, the point where they met is new pivot

Phân loại nhanh Pivot Pseudocode

Mã giả cho thuật toán trên có thể được suy ra là:

function partitionFunc(left, right, pivot)
   leftPointer = left
   rightPointer = right - 1

   while True do
      while A[++leftPointer] < pivot do
         //do-nothing            
      end while
		
      while rightPointer > 0 && A[--rightPointer] > pivot do
         //do-nothing         
      end while
		
      if leftPointer >= rightPointer
         break
      else                
         swap leftPointer,rightPointer
      end if
		
   end while 
	
   swap leftPointer,right
   return leftPointer
	
end function

Thuật toán sắp xếp nhanh

Sử dụng thuật toán pivot một cách đệ quy, chúng tôi kết thúc với các phân vùng nhỏ hơn có thể. Mỗi phân vùng sau đó được xử lý để sắp xếp nhanh chóng. Chúng tôi định nghĩa thuật toán đệ quy cho quicksort như sau:

Step 1 − Make the right-most index value pivot
Step 2 − partition the array using pivot value
Step 3 − quicksort left partition recursively
Step 4 − quicksort right partition recursively

Mã giả sắp xếp nhanh

Để hiểu thêm về nó, hãy xem mã giả cho thuật toán sắp xếp nhanh -

procedure quickSort(left, right)

   if right-left <= 0
      return
   else     
      pivot = A[right]
      partition = partitionFunc(left, right, pivot)
      quickSort(left,partition-1)
      quickSort(partition+1,right)    
   end if		
   
end procedure

Để biết về cách thực hiện sắp xếp nhanh trong ngôn ngữ lập trình C, vui lòng nhấp vào đây .

Đồ thị là một biểu diễn bằng hình ảnh của một tập hợp các đối tượng trong đó một số cặp đối tượng được nối với nhau bằng các liên kết. Các đối tượng được kết nối với nhau được biểu diễn bằng các điểm được gọi làverticesvà các liên kết nối các đỉnh được gọi là edges.

Về mặt hình thức, biểu đồ là một cặp tập hợp (V, E), Ở đâu V là tập hợp các đỉnh và Elà tập hợp các cạnh, nối các cặp đỉnh. Hãy xem biểu đồ sau:

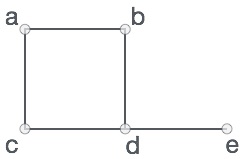
Trong biểu đồ trên,

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

Cấu trúc dữ liệu biểu đồ

Đồ thị toán học có thể được biểu diễn trong cấu trúc dữ liệu. Chúng ta có thể biểu diễn một đồ thị bằng cách sử dụng một mảng các đỉnh và một mảng hai chiều các cạnh. Trước khi tiếp tục, chúng ta hãy tự làm quen với một số thuật ngữ quan trọng -

• Vertex- Mỗi nút của đồ thị được biểu diễn dưới dạng một đỉnh. Trong ví dụ sau, vòng tròn được dán nhãn đại diện cho các đỉnh. Do đó, A đến G là các đỉnh. Chúng ta có thể biểu diễn chúng bằng một mảng như trong hình sau. Ở đây A có thể được xác định bằng chỉ số 0. B có thể được xác định bằng cách sử dụng chỉ số 1, v.v.

• Edge- Cạnh biểu diễn đường đi giữa hai đỉnh hoặc đường thẳng giữa hai đỉnh. Trong ví dụ sau, các dòng từ A đến B, B đến C, v.v. đại diện cho các cạnh. Chúng ta có thể sử dụng một mảng hai chiều để biểu diễn một mảng như trong hình sau. Ở đây AB có thể được biểu diễn dưới dạng 1 ở hàng 0, cột 1, BC là 1 ở hàng 1, cột 2, v.v., giữ các kết hợp khác là 0.

• Adjacency- Hai nút hoặc hai đỉnh kề nhau nếu chúng được nối với nhau qua một cạnh. Trong ví dụ sau, B là liền kề với A, C tiếp giáp với B, v.v.

• Path- Đường biểu diễn một dãy các cạnh giữa hai đỉnh. Trong ví dụ sau, ABCD biểu diễn một đường đi từ A đến D.

Hoạt động cơ bản

Sau đây là các hoạt động chính cơ bản của một Đồ thị:

• Add Vertex - Thêm một đỉnh vào đồ thị.

• Add Edge - Thêm một cạnh giữa hai đỉnh của đồ thị.

• Display Vertex - Hiển thị một đỉnh của đồ thị.

Để biết thêm về Đồ thị, vui lòng đọc Hướng dẫn Lý thuyết Đồ thị . Chúng ta sẽ tìm hiểu về việc duyệt qua một biểu đồ trong các chương tới.

Thuật toán Tìm kiếm đầu tiên theo chiều sâu (DFS) duyệt đồ thị theo chuyển động theo chiều sâu và sử dụng một ngăn xếp để ghi nhớ để lấy đỉnh tiếp theo để bắt đầu tìm kiếm, khi điểm cuối xảy ra trong bất kỳ lần lặp nào.

Như trong ví dụ được đưa ra ở trên, thuật toán DFS truyền từ S đến A đến D đến G đến E đến B trước, sau đó đến F và cuối cùng là C. Nó sử dụng các quy tắc sau.

• Rule 1- Ghé thăm đỉnh không được thăm liền kề. Đánh dấu nó là đã ghé thăm. Hiển thị nó. Đẩy nó vào một ngăn xếp.

• Rule 2- Nếu không tìm thấy đỉnh liền kề, bật lên một đỉnh từ ngăn xếp. (Nó sẽ bật lên tất cả các đỉnh từ ngăn xếp, những đỉnh không có các đỉnh liền kề.)

• Rule 3 - Lặp lại Quy tắc 1 và Quy tắc 2 cho đến khi ngăn xếp trống.

Bươc	Traversal	Sự miêu tả
1		Khởi tạo ngăn xếp.
2		dấu Snhư đã thăm và đặt nó vào ngăn xếp. Khám phá bất kỳ nút liền kề không được yêu cầu nào từS. Chúng tôi có ba nút và chúng tôi có thể chọn bất kỳ nút nào trong số đó. Đối với ví dụ này, chúng ta sẽ lấy nút theo thứ tự bảng chữ cái.
3		dấu Anhư đã thăm và đặt nó vào ngăn xếp. Khám phá bất kỳ nút liền kề không được mong đợi nào từ A. Cả haiS và D tiếp giáp với A nhưng chúng tôi chỉ lo lắng cho các nút không được truy cập.
4		Chuyến thăm Dvà đánh dấu nó là đã thăm và đặt vào ngăn xếp. Ở đây chúng tôi cóB và C các nút tiếp giáp với Dvà cả hai đều không được mời. Tuy nhiên, chúng ta sẽ chọn lại theo thứ tự bảng chữ cái.
5		Chúng tôi chọn B, đánh dấu nó là đã thăm và đặt vào ngăn xếp. ĐâyBkhông có bất kỳ nút liền kề nào chưa được truy cập. Vì vậy, chúng tôi bậtB từ ngăn xếp.
6		Chúng tôi kiểm tra đỉnh ngăn xếp để quay lại nút trước đó và kiểm tra xem nó có bất kỳ nút nào chưa được truy cập hay không. Ở đây, chúng tôi tìm thấyD ở trên cùng của ngăn xếp.
7		Chỉ có nút liền kề không được giám sát là từ D Là Chiện nay. Vì vậy, chúng tôi đến thămC, đánh dấu nó là đã thăm và đặt nó vào ngăn xếp.

Như Ckhông có bất kỳ nút liền kề nào chưa được duyệt, vì vậy chúng tôi tiếp tục bật ngăn xếp cho đến khi chúng tôi tìm thấy một nút có nút liền kề không được truy cập. Trong trường hợp này, không có gì và chúng tôi tiếp tục xuất hiện cho đến khi ngăn xếp trống.

Để biết về việc thực hiện thuật toán này trong ngôn ngữ lập trình C, hãy nhấp vào đây .

Thuật toán Tìm kiếm đầu tiên theo chiều rộng (BFS) duyệt qua một đồ thị theo chuyển động theo chiều rộng và sử dụng một hàng đợi để nhớ lấy đỉnh tiếp theo để bắt đầu tìm kiếm, khi một điểm cuối xảy ra trong bất kỳ lần lặp nào.

Như trong ví dụ được đưa ra ở trên, thuật toán BFS truyền từ A đến B đến E đến F trước rồi đến C và G cuối cùng đến D. Nó sử dụng các quy tắc sau.

• Rule 1- Ghé thăm đỉnh không được thăm liền kề. Đánh dấu nó là đã ghé thăm. Hiển thị nó. Chèn nó vào một hàng đợi.

• Rule 2 - Nếu không tìm thấy đỉnh liền kề, loại bỏ đỉnh đầu tiên khỏi hàng đợi.

• Rule 3 - Lặp lại Quy tắc 1 và Quy tắc 2 cho đến khi hàng đợi trống.

Bươc	Traversal	Sự miêu tả
1		Khởi tạo hàng đợi.
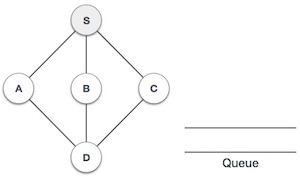
2		Chúng tôi bắt đầu từ thăm S (nút bắt đầu), và đánh dấu nó là đã truy cập.
3		Sau đó, chúng tôi thấy một nút liền kề không được sử dụng từ S. Trong ví dụ này, chúng tôi có ba nút nhưng chúng tôi chọn theo thứ tự bảng chữ cáiA, đánh dấu nó là đã ghé thăm và xếp hàng.
4		Tiếp theo, nút liền kề không được truy cập từ S Là B. Chúng tôi đánh dấu nó là đã ghé thăm và xếp hàng.
5		Tiếp theo, nút liền kề không được truy cập từ S Là C. Chúng tôi đánh dấu nó là đã ghé thăm và xếp hàng.
6		Hiện nay, Skhông có nút liền kề chưa được kiểm soát. Vì vậy, chúng tôi xếp hàng và tìmA.
7		Từ A chúng ta có Ddưới dạng nút liền kề không được kiểm soát. Chúng tôi đánh dấu nó là đã ghé thăm và xếp hàng.

Ở giai đoạn này, chúng ta không có nút nào chưa được đánh dấu (không được đánh dấu). Nhưng theo thuật toán, chúng tôi tiếp tục giảm giá trị để có được tất cả các nút chưa được sử dụng. Khi hàng đợi trống, chương trình kết thúc.

Việc thực hiện thuật toán này trong ngôn ngữ lập trình C có thể được xem tại đây .

Cây đại diện cho các nút được kết nối bởi các cạnh. Chúng ta sẽ thảo luận cụ thể về cây nhị phân hoặc cây tìm kiếm nhị phân.

Cây nhị phân là một cấu trúc dữ liệu đặc biệt được sử dụng cho mục đích lưu trữ dữ liệu. Cây nhị phân có một điều kiện đặc biệt là mỗi nút có thể có tối đa hai nút con. Cây nhị phân có lợi ích của cả mảng có thứ tự và danh sách được liên kết vì tìm kiếm nhanh như trong một mảng được sắp xếp và thao tác chèn hoặc xóa cũng nhanh như trong danh sách liên kết.

Điều khoản quan trọng

Sau đây là các điều khoản quan trọng đối với cây.

• Path - Đường dẫn đề cập đến chuỗi các nút dọc theo các cạnh của cây.

• Root- Nút ở ngọn cây gọi là gốc. Chỉ có một gốc trên mỗi cây và một đường dẫn từ nút gốc đến bất kỳ nút nào.

• Parent - Bất kỳ nút nào ngoại trừ nút gốc đều có một cạnh hướng lên trên một nút được gọi là cha.

• Child - Nút bên dưới một nút cho trước được nối bởi cạnh của nó hướng xuống được gọi là nút con của nó.

• Leaf - Nút không có nút con nào được gọi là nút lá.

• Subtree - Cây con đại diện cho con cháu của một nút.

• Visiting - Tham quan đề cập đến việc kiểm tra giá trị của một nút khi quyền điều khiển ở trên nút.

• Traversing - Đi ngang có nghĩa là đi qua các nút theo một thứ tự cụ thể.

• Levels- Mức của một nút thể hiện sự sinh ra của một nút. Nếu nút gốc ở mức 0, thì nút con tiếp theo của nó ở mức 1, nút cháu của nó ở mức 2, v.v.

• keys - Khóa đại diện cho một giá trị của một nút dựa trên đó hoạt động tìm kiếm sẽ được thực hiện cho một nút.

Biểu diễn cây tìm kiếm nhị phân

Cây tìm kiếm nhị phân thể hiện một hành vi đặc biệt. Nút con bên trái của nút phải có giá trị nhỏ hơn giá trị của nút cha và nút con bên phải của nút phải có giá trị lớn hơn giá trị mẹ của nó.

Chúng ta sẽ triển khai cây bằng cách sử dụng đối tượng nút và kết nối chúng thông qua các tham chiếu.

Nút cây

Mã để viết một nút cây sẽ tương tự như những gì được đưa ra bên dưới. Nó có một phần dữ liệu và các tham chiếu đến các nút con bên trái và bên phải của nó.

struct node {
   int data;   
   struct node *leftChild;
   struct node *rightChild;
};

Trong một cây, tất cả các nút đều có chung cấu trúc.

BST Các thao tác cơ bản

Các hoạt động cơ bản có thể được thực hiện trên cấu trúc dữ liệu cây tìm kiếm nhị phân, như sau:

• Insert - Chèn một phần tử vào cây / tạo cây.

• Search - Tìm kiếm một phần tử trong cây.

• Preorder Traversal - Đi ngang cây theo cách đặt hàng trước.

• Inorder Traversal - Đi ngang qua cây theo thứ tự.

• Postorder Traversal - Đi ngang cây theo thứ tự có sau.

Chúng ta sẽ học cách tạo (chèn vào) một cấu trúc cây và tìm kiếm một mục dữ liệu trong một cây trong chương này. Chúng ta sẽ tìm hiểu về các phương pháp duyệt cây trong chương tới.

Chèn hoạt động

Lần chèn đầu tiên tạo ra cây. Sau đó, bất cứ khi nào một phần tử được chèn vào, trước tiên hãy xác định vị trí thích hợp của nó. Bắt đầu tìm kiếm từ nút gốc, sau đó nếu dữ liệu nhỏ hơn giá trị khóa, hãy tìm kiếm vị trí trống trong cây con bên trái và chèn dữ liệu. Nếu không, hãy tìm kiếm vị trí trống trong cây con bên phải và chèn dữ liệu.

Thuật toán

If root is NULL 
   then create root node
return

If root exists then
   compare the data with node.data
   
   while until insertion position is located

      If data is greater than node.data
         goto right subtree
      else
         goto left subtree

   endwhile 
   
   insert data
	
end If

Thực hiện

Việc thực hiện chức năng chèn sẽ giống như sau:

void insert(int data) {
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty, create root node
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent  = NULL;

      while(1) {                
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;                
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }
			
         //go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}

Hoạt động tìm kiếm

Bất cứ khi nào một phần tử được tìm kiếm, hãy bắt đầu tìm kiếm từ nút gốc, sau đó nếu dữ liệu nhỏ hơn giá trị khóa, hãy tìm kiếm phần tử trong cây con bên trái. Nếu không, hãy tìm kiếm phần tử trong cây con bên phải. Thực hiện theo cùng một thuật toán cho mỗi nút.

Thuật toán

If root.data is equal to search.data
   return root
else
   while data not found

      If data is greater than node.data
         goto right subtree
      else
         goto left subtree
         
      If data found
         return node
   endwhile 
   
   return data not found
   
end if

Việc triển khai thuật toán này sẽ trông như thế này.

struct node* search(int data) {
   struct node *current = root;
   printf("Visiting elements: ");

   while(current->data != data) {
      if(current != NULL)
      printf("%d ",current->data); 
      
      //go to left tree

      if(current->data > data) {
         current = current->leftChild;
      }
      //else go to right tree
      else {                
         current = current->rightChild;
      }

      //not found
      if(current == NULL) {
         return NULL;
      }

      return current;
   }  
}

Để biết về việc thực hiện cấu trúc dữ liệu cây tìm kiếm nhị phân, vui lòng nhấp vào đây .

Traversal là một quá trình để truy cập tất cả các nút của cây và có thể in ra các giá trị của chúng. Bởi vì, tất cả các nút được kết nối thông qua các cạnh (liên kết) chúng ta luôn bắt đầu từ nút gốc (đầu). Tức là chúng ta không thể truy cập ngẫu nhiên vào một nút trong cây. Có ba cách mà chúng tôi sử dụng để đi qua một cái cây -

• Traversal theo thứ tự
• Đặt trước Traversal
• Traversal đặt hàng sau

Nói chung, chúng tôi đi qua một cây để tìm kiếm hoặc định vị một mục hoặc khóa nhất định trong cây hoặc để in tất cả các giá trị mà nó chứa.

Traversal theo thứ tự

Trong phương pháp duyệt này, cây con bên trái được truy cập đầu tiên, sau đó đến gốc và sau đó là cây con bên phải. Chúng ta nên nhớ rằng mỗi nút có thể đại diện cho chính một cây con.

Nếu một cây nhị phân được duyệt qua in-order, đầu ra sẽ tạo ra các giá trị khóa được sắp xếp theo thứ tự tăng dần.

Chúng tôi bắt đầu từ Avà sau khi duyệt theo thứ tự, chúng tôi chuyển sang cây con bên trái của nó B. Bcũng được duyệt theo thứ tự. Quá trình tiếp tục cho đến khi tất cả các nút được truy cập. Đầu ra của việc di chuyển ngang qua cây này sẽ là:

D → B → E → A → F → C → G

Thuật toán

Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Visit root node.
Step 3 − Recursively traverse right subtree.

Đặt trước Traversal

Trong phương pháp duyệt này, nút gốc được truy cập đầu tiên, sau đó đến cây con bên trái và cuối cùng là cây con bên phải.

Chúng tôi bắt đầu từ Avà sau khi duyệt đơn đặt hàng trước, trước tiên chúng tôi truy cập A chính nó và sau đó chuyển sang cây con bên trái của nó B. Bcũng là đơn đặt hàng trước được duyệt. Quá trình tiếp tục cho đến khi tất cả các nút được truy cập. Đầu ra của việc duyệt đơn đặt hàng trước của cây này sẽ là:

A → B → D → E → C → F → G

Thuật toán

Until all nodes are traversed −
Step 1 − Visit root node.
Step 2 − Recursively traverse left subtree.
Step 3 − Recursively traverse right subtree.

Traversal đặt hàng sau

Trong phương thức truyền tải này, nút gốc được truy cập cuối cùng, do đó có tên. Đầu tiên chúng ta duyệt qua cây con bên trái, sau đó đến cây con bên phải và cuối cùng là nút gốc.

Chúng tôi bắt đầu từ Avà sau khi duyệt qua Đơn đặt hàng sau, trước tiên chúng ta truy cập vào cây con bên trái B. Bcũng được duyệt qua đơn đặt hàng sau. Quá trình tiếp tục cho đến khi tất cả các nút được truy cập. Kết quả của việc duyệt sau đơn hàng của cây này sẽ là:

D → E → B → F → G → C → A

Thuật toán

Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Recursively traverse right subtree.
Step 3 − Visit root node.

Để kiểm tra việc triển khai C của việc duyệt cây, vui lòng nhấp vào đây .

Cây tìm kiếm nhị phân (BST) là cây trong đó tất cả các nút tuân theo các thuộc tính được đề cập dưới đây:

• Giá trị của khóa của cây con bên trái nhỏ hơn giá trị của khóa của nút cha (gốc) của nó.

• Giá trị của khóa của cây con bên phải lớn hơn hoặc bằng giá trị của khóa của nút cha (gốc) của nó.

Như vậy, BST chia tất cả các cây con của nó thành hai phân đoạn; cây con bên trái và cây con bên phải và có thể được định nghĩa là -

left_subtree (keys) < node (key) ≤ right_subtree (keys)

Đại diện

BST là tập hợp các nút được sắp xếp theo cách mà chúng duy trì các thuộc tính của BST. Mỗi nút có một khóa và một giá trị liên quan. Trong khi tìm kiếm, khóa mong muốn được so sánh với các khóa trong BST và nếu được tìm thấy, giá trị liên quan sẽ được truy xuất.

Sau đây là hình ảnh đại diện của BST -

Chúng ta quan sát thấy khóa của nút gốc (27) có tất cả các khóa có giá trị thấp hơn trên cây con bên trái và các khóa có giá trị cao hơn trên cây con bên phải.

Hoạt động cơ bản

Sau đây là các hoạt động cơ bản của cây:

• Search - Tìm kiếm một phần tử trong cây.

• Insert - Chèn một phần tử trong cây.

• Pre-order Traversal - Đi ngang cây theo cách đặt hàng trước.

• In-order Traversal - Đi ngang qua cây theo thứ tự.

• Post-order Traversal - Đi ngang cây theo thứ tự có sau.

Nút

Xác định một nút có một số dữ liệu, tham chiếu đến các nút con bên trái và bên phải của nó.

struct node {
   int data;   
   struct node *leftChild;
   struct node *rightChild;
};

Hoạt động tìm kiếm

Bất cứ khi nào một phần tử được tìm kiếm, hãy bắt đầu tìm kiếm từ nút gốc. Sau đó, nếu dữ liệu nhỏ hơn giá trị khóa, hãy tìm kiếm phần tử trong cây con bên trái. Nếu không, hãy tìm kiếm phần tử trong cây con bên phải. Thực hiện theo cùng một thuật toán cho mỗi nút.

Thuật toán

struct node* search(int data){
   struct node *current = root;
   printf("Visiting elements: ");
	
   while(current->data != data){
	
      if(current != NULL) {
         printf("%d ",current->data);
			
         //go to left tree
         if(current->data > data){
            current = current->leftChild;
         }  //else go to right tree
         else {                
            current = current->rightChild;
         }
			
         //not found
         if(current == NULL){
            return NULL;
         }
      }			
   }
   
   return current;
}

Chèn hoạt động

Bất cứ khi nào một phần tử được chèn vào, trước tiên hãy xác định vị trí thích hợp của nó. Bắt đầu tìm kiếm từ nút gốc, sau đó nếu dữ liệu nhỏ hơn giá trị khóa, hãy tìm kiếm vị trí trống trong cây con bên trái và chèn dữ liệu. Nếu không, hãy tìm kiếm vị trí trống trong cây con bên phải và chèn dữ liệu.

Thuật toán

void insert(int data) {
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;

      while(1) {                
         parent = current;
			
         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;                
            //insert to the left
				
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }  //go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}

Điều gì sẽ xảy ra nếu đầu vào cho cây tìm kiếm nhị phân theo cách được sắp xếp (tăng dần hoặc giảm dần)? Sau đó nó sẽ giống như thế này -

Quan sát thấy rằng hiệu suất trong trường hợp xấu nhất của BST gần nhất với các thuật toán tìm kiếm tuyến tính, đó là Ο (n). Trong dữ liệu thời gian thực, chúng tôi không thể dự đoán mẫu dữ liệu và tần số của chúng. Vì vậy, một nhu cầu phát sinh để cân bằng BST hiện có.

Được đặt tên theo nhà phát minh của họ Adelson, Velski & Landis, AVL treeslà cây tìm kiếm nhị phân cân bằng chiều cao. Cây AVL kiểm tra chiều cao của cây con bên trái và bên phải và đảm bảo rằng sự khác biệt không quá 1. Sự khác biệt này được gọi làBalance Factor.

Ở đây ta thấy rằng cây đầu tiên cân bằng và hai cây tiếp theo không cân bằng -

Trong cây thứ hai, cây con bên trái của C có chiều cao 2 và cây con bên phải có chiều cao 0, do đó hiệu là 2. Trong cây thứ ba, cây con bên phải của Acó chiều cao 2 và bên trái bị thiếu, do đó, nó là 0, và sự khác biệt là 2 một lần nữa. Cây AVL cho phép chênh lệch (hệ số cân bằng) chỉ là 1.

BalanceFactor = height(left-sutree) − height(right-sutree)

Nếu sự khác biệt về chiều cao của các cây phụ bên trái và bên phải lớn hơn 1 thì cây được cân đối bằng một số kỹ thuật luân canh.

Vòng quay AVL

Để tự cân bằng, cây AVL có thể thực hiện bốn kiểu xoay sau:

• Xoay trái
• Xoay phải
• Xoay trái-phải
• Xoay phải-trái

Hai phép quay đầu tiên là phép quay đơn và hai phép quay tiếp theo là phép quay kép. Để có một cây không cân đối, ít nhất chúng ta cần một cây có chiều cao bằng 2. Với loại cây đơn giản này, chúng ta hãy hiểu từng loại một.

Xoay trái

Nếu một cây trở nên không cân bằng, khi một nút được chèn vào cây con bên phải của cây con bên phải, thì chúng ta thực hiện một phép quay sang trái duy nhất -

Trong ví dụ của chúng tôi, nút Ađã trở nên không cân bằng khi một nút được chèn vào cây con bên phải của cây con bên phải của A. Chúng tôi thực hiện xoay trái bằng cáchA cây con bên trái của B.

Xoay phải

Cây AVL có thể trở nên không cân bằng, nếu một nút được chèn vào cây con bên trái của cây con bên trái. Khi đó cây cần phải luân chuyển đúng cách.

Như được mô tả, nút không cân bằng trở thành nút con bên phải của nút con bên trái của nó bằng cách thực hiện quay phải.

Xoay trái-phải

Phép quay kép là phiên bản hơi phức tạp của các phiên bản xoay đã được giải thích. Để hiểu rõ hơn về chúng, chúng ta nên lưu ý từng hành động được thực hiện trong khi xoay. Đầu tiên chúng ta hãy kiểm tra cách thực hiện xoay Trái-Phải. Xoay trái-phải là sự kết hợp của xoay trái sau đó xoay phải.

Tiểu bang	Hoạt động
	Một nút đã được chèn vào cây con bên phải của cây con bên trái. Điều này làm choCmột nút không cân bằng. Các kịch bản này khiến cây AVL thực hiện xoay trái-phải.
	Đầu tiên chúng tôi thực hiện xoay trái trên cây con bên trái của C. Điều này làm choA, cây con bên trái của B.
	Nút C vẫn không cân bằng, tuy nhiên bây giờ, đó là do cây con bên trái của cây con bên trái.
	Bây giờ chúng ta sẽ xoay cây sang phải, làm cho B nút gốc mới của cây con này. C bây giờ trở thành cây con bên phải của cây con bên trái của chính nó.
	Hiện cây đã cân đối.

Xoay phải-trái

Kiểu quay kép thứ hai là Xoay phải-Trái. Nó là sự kết hợp của xoay phải sau đó xoay trái.

Tiểu bang	Hoạt động
	Một nút đã được chèn vào cây con bên trái của cây con bên phải. Điều này làm choA, một nút không cân bằng với hệ số cân bằng 2.
	Đầu tiên, chúng tôi thực hiện xoay bên phải dọc theo C nút, làm C cây con bên phải của cây con bên trái của chính nó B. Hiện nay,B trở thành cây con bên phải của A.
	Nút A vẫn không cân bằng vì cây con bên phải của cây con bên phải của nó và yêu cầu quay trái.
	Xoay trái được thực hiện bằng cách B nút gốc mới của cây con. A trở thành cây con bên trái của cây con bên phải của nó B.
	Hiện cây đã cân đối.

Cây khung là một tập con của Đồ thị G, có tất cả các đỉnh được phủ với số cạnh tối thiểu có thể. Do đó, cây khung không có chu kỳ và nó không thể bị ngắt kết nối ..

Theo định nghĩa này, chúng ta có thể rút ra kết luận rằng mọi Đồ thị G được kết nối và vô hướng đều có ít nhất một cây khung. Một đồ thị bị ngắt kết nối không có bất kỳ cây khung nào, vì nó không thể được mở rộng đến tất cả các đỉnh của nó.

Chúng tôi tìm thấy ba cây bao trùm trên một biểu đồ hoàn chỉnh. Một biểu đồ vô hướng hoàn chỉnh có thể cón^n-2 số lượng cây bao trùm, ở đâu nlà số lượng nút. Trong ví dụ được giải quyết ở trên,n is 3, vì thế 3³⁻² = 3 cây kéo dài là có thể.

Thuộc tính chung của cây kéo dài

Bây giờ chúng ta hiểu rằng một biểu đồ có thể có nhiều hơn một cây bao trùm. Sau đây là một vài thuộc tính của cây khung được kết nối với đồ thị G -

• Một đồ thị liên thông G có thể có nhiều hơn một cây khung.

• Tất cả các cây khung có thể có của đồ thị G, có cùng số cạnh và đỉnh.

• Cây khung không có bất kỳ chu trình (vòng lặp) nào.

• Loại bỏ một cạnh khỏi cây khung sẽ làm cho đồ thị bị ngắt kết nối, tức là cây bao trùm là minimally connected.

• Thêm một cạnh vào cây khung sẽ tạo ra một mạch hoặc vòng lặp, tức là cây bao trùm là maximally acyclic.

Tính chất toán học của cây kéo dài

• Cây kéo dài có n-1 các cạnh, ở đâu n là số nút (đỉnh).

• Từ một biểu đồ hoàn chỉnh, bằng cách loại bỏ tối đa e - n + 1 các cạnh, chúng ta có thể xây dựng một cây bao trùm.

• Một biểu đồ hoàn chỉnh có thể có giá trị tối đa n^n-2 số cây bao trùm.

Do đó, chúng ta có thể kết luận rằng cây khung là một tập con của Đồ thị G được kết nối và các đồ thị bị ngắt kết nối không có cây khung.

Ứng dụng của cây kéo dài

Spanning tree về cơ bản được sử dụng để tìm một đường dẫn tối thiểu để kết nối tất cả các nút trong một đồ thị. Ứng dụng phổ biến của cây bao trùm là -

• Civil Network Planning

• Computer Network Routing Protocol

• Cluster Analysis

Hãy để chúng tôi hiểu điều này qua một ví dụ nhỏ. Hãy xem xét, mạng lưới thành phố như một biểu đồ khổng lồ và hiện có kế hoạch triển khai các đường dây điện thoại theo cách mà trong các đường dây tối thiểu chúng ta có thể kết nối với tất cả các nút của thành phố. Đây là lúc cây bao trùm đi vào hình ảnh.

Cây kéo dài tối thiểu (MST)

Trong đồ thị có trọng số, cây bao trùm tối thiểu là cây bao trùm có trọng số tối thiểu hơn tất cả các cây bao trùm khác của cùng một đồ thị. Trong các tình huống thực tế, trọng số này có thể được đo dưới dạng khoảng cách, tắc nghẽn, tải trọng giao thông hoặc bất kỳ giá trị tùy ý nào được biểu thị cho các cạnh.

Thuật toán cây kéo dài tối thiểu

Chúng ta sẽ tìm hiểu về hai thuật toán cây bao trùm quan trọng nhất ở đây -

• Thuật toán Kruskal

• Thuật toán của Prim

Cả hai đều là các thuật toán tham lam.

Heap là một trường hợp đặc biệt của cấu trúc dữ liệu cây nhị phân cân bằng trong đó khóa của nút gốc được so sánh với các nút con của nó và được sắp xếp cho phù hợp. Nếuα có nút con β sau đó -

phím (α) ≥ phím (β)

Vì giá trị của cha lớn hơn giá trị của con, thuộc tính này tạo ra Max Heap. Dựa trên tiêu chí này, một đống có thể có hai loại -

For Input → 35 33 42 10 14 19 27 44 26 31

Min-Heap - Trường hợp giá trị của nút gốc nhỏ hơn hoặc bằng một trong hai nút con của nó.

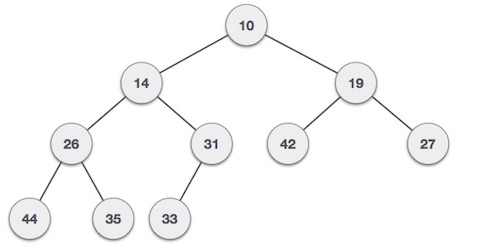
Max-Heap - Trường hợp giá trị của nút gốc lớn hơn hoặc bằng một trong hai nút con của nó.

Cả hai cây đều được xây dựng bằng cách sử dụng cùng một đầu vào và thứ tự đến.

Thuật toán xây dựng đống tối đa

Chúng ta sẽ sử dụng cùng một ví dụ để chứng minh cách tạo Max Heap. Quy trình tạo Min Heap cũng tương tự nhưng chúng ta chọn giá trị min thay vì giá trị max.

Chúng tôi sẽ tìm ra một thuật toán cho đống tối đa bằng cách chèn một phần tử tại một thời điểm. Tại bất kỳ thời điểm nào, heap phải duy trì tài sản của nó. Trong khi chèn, chúng tôi cũng giả định rằng chúng tôi đang chèn một nút trong một cây đã được xếp sẵn.

Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.

Note - Trong thuật toán xây dựng Min Heap, chúng ta mong muốn giá trị của nút cha nhỏ hơn giá trị của nút con.

Hãy hiểu cách xây dựng Max Heap bằng một minh họa động. Chúng tôi xem xét cùng một mẫu đầu vào mà chúng tôi đã sử dụng trước đó.

Thuật toán xóa đống tối đa

Hãy để chúng tôi suy ra một thuật toán để xóa khỏi đống tối đa. Xóa trong đống Max (hoặc Min) luôn luôn xảy ra ở gốc để loại bỏ giá trị Tối đa (hoặc nhỏ nhất).

Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.

Một số ngôn ngữ lập trình máy tính cho phép một mô-đun hoặc hàm gọi chính nó. Kỹ thuật này được gọi là đệ quy. Trong đệ quy, một hàmα gọi chính nó trực tiếp hoặc gọi một hàm β đến lượt nó gọi hàm ban đầu α. Chức năngα được gọi là hàm đệ quy.

Example - một hàm gọi chính nó.

int function(int value) {
   if(value < 1)
      return;
   function(value - 1);

   printf("%d ",value);   
}

Example - một hàm gọi một hàm khác mà lần lượt nó sẽ gọi lại.

int function1(int value1) {
   if(value1 < 1)
      return;
   function2(value1 - 1);
   printf("%d ",value1);   
}
int function2(int value2) {
   function1(value2);
}

Tính chất

Một hàm đệ quy có thể đi vô hạn giống như một vòng lặp. Để tránh chạy vô hạn hàm đệ quy, có hai thuộc tính mà một hàm đệ quy phải có:

• Base criteria - Phải có ít nhất một tiêu chí hoặc điều kiện cơ sở, sao cho khi điều kiện này được đáp ứng, hàm ngừng gọi chính nó một cách đệ quy.

• Progressive approach - Các cuộc gọi đệ quy phải tiến triển theo cách mà mỗi lần gọi đệ quy được thực hiện thì nó lại gần với tiêu chí cơ sở hơn.

Thực hiện

Nhiều ngôn ngữ lập trình thực hiện đệ quy bằng cách stacks. Nói chung, bất cứ khi nào một hàm (caller) gọi một hàm khác (callee) hoặc chính nó là callee, hàm người gọi chuyển quyền kiểm soát thực thi đến callee. Quá trình chuyển giao này cũng có thể liên quan đến một số dữ liệu được chuyển từ người gọi đến người gọi.

Điều này ngụ ý rằng, hàm người gọi phải tạm ngừng thực thi và tiếp tục lại sau khi điều khiển thực thi trả về từ hàm callee. Ở đây, hàm người gọi cần bắt đầu chính xác từ thời điểm thực thi mà nó tự đặt nó ở trạng thái chờ. Nó cũng cần các giá trị dữ liệu chính xác giống như nó đã hoạt động. Với mục đích này, một bản ghi kích hoạt (hoặc khung ngăn xếp) được tạo cho hàm người gọi.

Bản ghi kích hoạt này giữ thông tin về các biến cục bộ, các tham số chính thức, địa chỉ trả về và tất cả thông tin được chuyển đến hàm người gọi.

Phân tích đệ quy

Người ta có thể tranh luận tại sao phải sử dụng đệ quy, vì cùng một nhiệm vụ có thể được thực hiện với phép lặp. Lý do đầu tiên là, đệ quy làm cho một chương trình dễ đọc hơn và vì các hệ thống CPU cải tiến mới nhất, đệ quy hiệu quả hơn so với lặp lại.

Thời gian phức tạp

Trong trường hợp lặp lại, chúng tôi lấy số lần lặp để đếm độ phức tạp về thời gian. Tương tự như vậy, trong trường hợp đệ quy, giả sử mọi thứ là không đổi, chúng tôi cố gắng tìm ra số lần một lệnh gọi đệ quy được thực hiện. Một lệnh gọi hàm là Ο (1), do đó (n) số lần lệnh gọi đệ quy được thực hiện làm cho hàm đệ quy Ο (n).

Không gian phức tạp

Độ phức tạp của không gian được tính là lượng không gian bổ sung cần thiết để mô-đun thực thi. Trong trường hợp lặp lại, trình biên dịch hầu như không yêu cầu thêm dung lượng. Trình biên dịch tiếp tục cập nhật giá trị của các biến được sử dụng trong các lần lặp. Nhưng trong trường hợp đệ quy, hệ thống cần lưu trữ bản ghi kích hoạt mỗi khi thực hiện cuộc gọi đệ quy. Do đó, có thể coi độ phức tạp về không gian của hàm đệ quy có thể cao hơn so với hàm có lặp.

Tháp Hà Nội, là một câu đố toán học bao gồm ba tháp (chốt) và nhiều hơn một vòng được mô tả -

Những chiếc nhẫn này có kích thước khác nhau và xếp chồng lên nhau theo thứ tự tăng dần, tức là chiếc nhỏ hơn nằm trên chiếc lớn hơn. Có những biến thể khác của câu đố trong đó số lượng đĩa tăng lên, nhưng số tháp vẫn giữ nguyên.

Quy tắc

Nhiệm vụ là di chuyển tất cả các đĩa đến một số tháp khác mà không vi phạm trình tự sắp xếp. Một số quy tắc cần tuân thủ đối với Tháp Hà Nội là:

• Chỉ có thể di chuyển một đĩa giữa các tháp vào bất kỳ thời điểm nào.
• Chỉ đĩa "trên cùng" mới có thể được gỡ bỏ.
• Không có đĩa lớn nào có thể đè lên đĩa nhỏ.

Sau đây là mô tả hoạt hình giải câu đố Tháp Hà Nội bằng ba đĩa.

Câu đố Tháp Hà Nội với tối thiểu n đĩa có thể giải được 2ⁿ−1các bước. Phần trình bày này cho thấy rằng một câu đố với 3 đĩa đã được2³ - 1 = 7 các bước.

Thuật toán

Để viết một thuật toán cho Tower of Hanoi, trước tiên chúng ta cần tìm hiểu cách giải bài toán này với số lượng đĩa ít hơn, giả sử → 1 hoặc 2. Chúng ta đánh dấu ba tháp bằng tên, source, destination và aux(chỉ để giúp di chuyển các đĩa). Nếu chúng ta chỉ có một đĩa, thì nó có thể dễ dàng di chuyển từ nguồn đến chốt đích.

Nếu chúng ta có 2 đĩa -

• Đầu tiên, chúng tôi di chuyển đĩa nhỏ hơn (trên cùng) sang aux peg.
• Sau đó, chúng tôi di chuyển đĩa lớn hơn (dưới cùng) đến chốt đích.
• Và cuối cùng, chúng tôi di chuyển đĩa nhỏ hơn từ aux đến chốt đích.

Vì vậy, bây giờ, chúng tôi đang ở vị trí để thiết kế một thuật toán cho Tower of Hanoi với hơn hai đĩa. Chúng tôi chia chồng đĩa thành hai phần. Đĩa lớn nhất (đĩa ^thứ n ) nằm trong một phần và tất cả các đĩa (n-1) khác nằm trong phần thứ hai.

Mục đích cuối cùng của chúng tôi là di chuyển đĩa ntừ nguồn đến đích và sau đó đặt tất cả (n1) đĩa khác vào đó. Chúng ta có thể tưởng tượng áp dụng giống nhau theo cách đệ quy cho tất cả các bộ đĩa đã cho.

Các bước cần làm là -

Step 1 − Move n-1 disks from source to aux
Step 2 − Move nth disk from source to dest
Step 3 − Move n-1 disks from aux to dest

Một thuật toán đệ quy cho Tower of Hanoi có thể được định hướng như sau:

START
Procedure Hanoi(disk, source, dest, aux)

   IF disk == 1, THEN
      move disk from source to dest             
   ELSE
      Hanoi(disk - 1, source, aux, dest)     // Step 1
      move disk from source to dest          // Step 2
      Hanoi(disk - 1, aux, dest, source)     // Step 3
   END IF
   
END Procedure
STOP

Để kiểm tra việc thực hiện trong lập trình C, hãy nhấp vào đây .

Chuỗi Fibonacci tạo ra số tiếp theo bằng cách thêm hai số trước đó. Chuỗi Fibonacci bắt đầu từ hai số -F₀ & F₁. Các giá trị ban đầu của F ₀ & F ₁ có thể được lấy tương ứng là 0, 1 hoặc 1, 1.

Chuỗi Fibonacci thỏa mãn các điều kiện sau:

Fn = Fn-1 + Fn-2

Do đó, một chuỗi Fibonacci có thể trông như thế này -

F ₈ = 0 1 1 2 3 5 8 13

hoặc, cái này -

F ₈ = 1 1 2 3 5 8 13 21

Với mục đích minh họa, Fibonacci của F ₈ được hiển thị dưới dạng:

Thuật toán lặp lại Fibonacci

Đầu tiên, chúng tôi cố gắng soạn thảo thuật toán lặp lại cho chuỗi Fibonacci.

Procedure Fibonacci(n)
   declare f0, f1, fib, loop 
   
   set f0 to 0
   set f1 to 1
   
   display f0, f1
   
   for loop ← 1 to n
   
      fib ← f0 + f1   
      f0 ← f1
      f1 ← fib

      display fib
   end for
	
end procedure

Để biết về cách thực hiện thuật toán trên trong ngôn ngữ lập trình C, hãy nhấp vào đây .

Thuật toán đệ quy Fibonacci

Hãy cùng chúng tôi tìm hiểu cách tạo chuỗi Fibonacci thuật toán đệ quy. Các tiêu chí cơ bản của đệ quy.

START
Procedure Fibonacci(n)
   declare f0, f1, fib, loop 
   
   set f0 to 0
   set f1 to 1
   
   display f0, f1
   
   for loop ← 1 to n
   
      fib ← f0 + f1   
      f0 ← f1
      f1 ← fib

      display fib
   end for

END

Để xem cách thực hiện thuật toán trên trong ngôn ngữ lập trình c, bấm vào đây .