Lý thuyết đồ thị - Khả năng kết nối
Việc có thể đi ngang một đồ thị từ đỉnh này sang đỉnh khác hay không được xác định bởi cách một đồ thị được kết nối. Kết nối là một khái niệm cơ bản trong Lý thuyết đồ thị. Khả năng kết nối xác định xem một biểu đồ được kết nối hay bị ngắt kết nối. Nó có các chủ đề phụ dựa trên cạnh và đỉnh, được gọi là kết nối cạnh và kết nối đỉnh. Hãy để chúng tôi thảo luận chi tiết về chúng.
Kết nối
Một biểu đồ được cho là connected if there is a path between every pair of vertex. Từ mọi đỉnh đến bất kỳ đỉnh nào khác, phải có một số đường đi qua. Đó được gọi là khả năng kết nối của một đồ thị. Một đồ thị có nhiều đỉnh và cạnh bị ngắt kết nối được cho là bị ngắt kết nối.
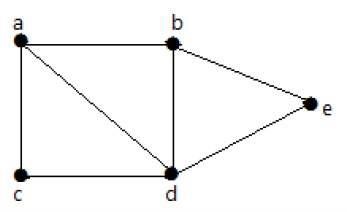
Example 1
Trong đồ thị sau, có thể đi từ đỉnh này sang bất kỳ đỉnh nào khác. Ví dụ, người ta có thể đi qua đỉnh 'a' đến đỉnh 'e' bằng cách sử dụng đường dẫn 'ab-e'.
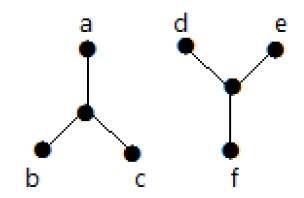
Example 2
Trong ví dụ sau, không thể đi ngang từ đỉnh 'a' đến đỉnh 'f' vì không có đường đi giữa chúng trực tiếp hoặc gián tiếp. Do đó nó là một đồ thị bị ngắt kết nối.
Cắt đỉnh
Gọi 'G' là một đồ thị liên thông. Đỉnh V ∈ G được gọi là đỉnh cắt của 'G', nếu 'G-V' (Xóa 'V' khỏi 'G') dẫn đến một đồ thị bị ngắt. Xóa một đỉnh cắt khỏi biểu đồ sẽ chia nó thành hai hoặc nhiều đồ thị.
Note - Loại bỏ một đỉnh bị cắt có thể làm cho một đồ thị bị ngắt kết nối.
Một đồ thị liên thông 'G' có thể có nhiều nhất (n – 2) đỉnh cắt.
Example
Trong đồ thị sau, các đỉnh 'e' và 'c' là các đỉnh cắt.

Bằng cách loại bỏ 'e' hoặc 'c', đồ thị sẽ trở thành đồ thị bị ngắt kết nối.

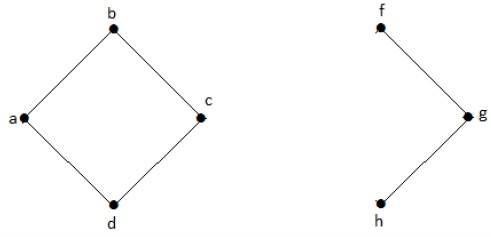
Không có 'g', không có đường đi giữa đỉnh 'c' và đỉnh 'h' và nhiều đường khác. Do đó nó là một đồ thị không kết nối với đỉnh cắt là 'e'. Tương tự, 'c' cũng là một đỉnh cắt của đồ thị trên.
Cắt cạnh (Cầu)
Gọi 'G' là một đồ thị liên thông. Một cạnh 'e' ∈ G được gọi là một cạnh cắt nếu 'G-e' dẫn đến một đồ thị bị ngắt kết nối.
Nếu loại bỏ một cạnh trong biểu đồ dẫn đến hai hoặc nhiều đồ thị, thì cạnh đó được gọi là Cạnh cắt.
Example
Trong đồ thị sau, cạnh bị cắt là [(c, e)].

Bằng cách loại bỏ cạnh (c, e) khỏi đồ thị, nó sẽ trở thành một đồ thị bị ngắt kết nối.


Trong đồ thị trên, việc loại bỏ cạnh (c, e) sẽ phá vỡ đồ thị thành hai, không có gì khác ngoài một đồ thị bị ngắt kết nối. Do đó, cạnh (c, e) là một cạnh cắt của đồ thị.
Note - Gọi 'G' là một đồ thị liên thông với 'n' đỉnh, khi đó
một cạnh cắt e ∈ G nếu và chỉ khi cạnh 'e' không phải là một phần của bất kỳ chu trình nào trong G.
số cạnh cắt tối đa có thể là 'n-1'.
bất cứ khi nào các cạnh cắt tồn tại, các đỉnh bị cắt cũng tồn tại vì ít nhất một đỉnh của một cạnh cắt là một đỉnh cắt.
nếu một đỉnh cắt tồn tại, thì một cạnh cắt có thể tồn tại hoặc không.
Cắt một bộ đồ thị
Gọi 'G' = (V, E) là một đồ thị liên thông. Tập con E 'của E được gọi là tập cắt của G nếu việc xóa tất cả các cạnh của E' khỏi G làm cho G bị ngắt.
Nếu việc xóa một số cạnh nhất định khỏi đồ thị làm cho nó bị ngắt kết nối, thì các cạnh bị xóa đó được gọi là tập cắt của đồ thị.
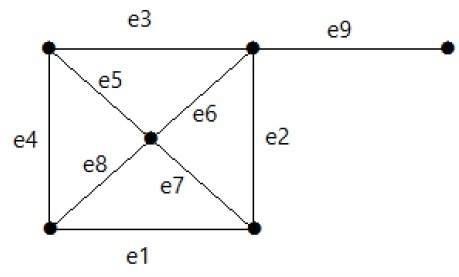
Example
Hãy xem biểu đồ sau. Tập hợp cắt của nó là E1 = {e1, e3, e5, e8}.
Sau khi loại bỏ tập cắt E1 khỏi biểu đồ, nó sẽ xuất hiện như sau:
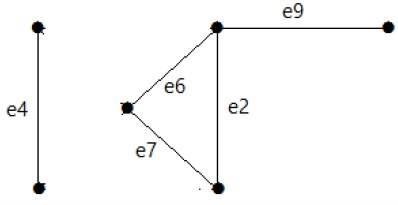
Tương tự, có những tập hợp cắt khác có thể ngắt kết nối đồ thị -
E3 = {e9} - Tập hợp cắt nhỏ nhất của đồ thị.
E4 = {e3, e4, e5}
Kết nối cạnh
Gọi 'G' là một đồ thị liên thông. Số cạnh tối thiểu mà việc loại bỏ làm cho 'G' bị ngắt kết nối được gọi là kết nối cạnh của G.
Notation - λ (G)
Nói cách khác, number of edges in a smallest cut set of G được gọi là kết nối cạnh của G.
Nếu 'G' có một cạnh cắt thì λ (G) là 1. (kết nối cạnh của G.)
Example
Hãy xem biểu đồ sau. Bằng cách loại bỏ hai cạnh nhỏ nhất, đồ thị được kết nối sẽ bị ngắt kết nối. Do đó, kết nối cạnh của nó (λ (G)) là 2.
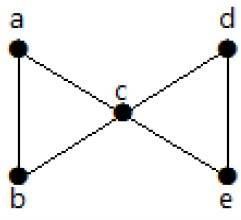
Dưới đây là bốn cách để ngắt kết nối biểu đồ bằng cách loại bỏ hai cạnh -

Kết nối đỉnh
Gọi 'G' là một đồ thị liên thông. Số lượng đỉnh tối thiểu mà việc loại bỏ làm cho 'G' bị ngắt kết nối hoặc giảm 'G' vào một đồ thị nhỏ được gọi là kết nối đỉnh của nó.
Notation - K (G)
Example
Trong đồ thị trên, việc loại bỏ các đỉnh 'e' và 'i' làm cho đồ thị bị ngắt kết nối.

Nếu G có đỉnh cắt thì K (G) = 1.
Notation - Đối với bất kỳ đồ thị liên thông G,
K (G) ≤ λ (G) ≤ δ (G)
Kết nối đỉnh (K (G)), kết nối cạnh (λ (G)), số độ tối thiểu của G (δ (G)).
Example
Tính λ (G) và K (G) cho đồ thị sau:
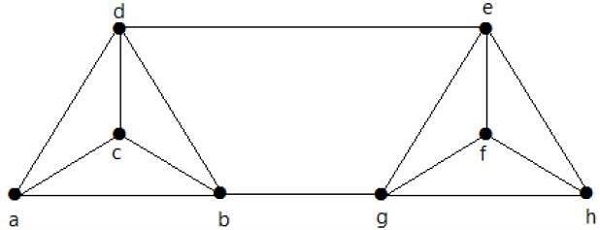
Solution
Từ biểu đồ,
δ (G) = 3
K (G) ≤ λ (G) ≤ δ (G) = 3 (1)
K (G) ≥ 2 (2)
Xóa các cạnh {d, e} và {b, h}, chúng ta có thể ngắt kết nối G.
Vì thế,
λ (G) = 2
2 ≤ λ (G) ≤ δ (G) = 2 (3)
Từ (2) và (3), kết nối đỉnh K (G) = 2