Lý thuyết đồ thị - Nguyên tắc cơ bản

Đồ thị là một sơ đồ gồm các điểm và các đường thẳng nối với các điểm. Nó có ít nhất một dòng nối một tập hợp hai đỉnh mà không có đỉnh nào nối chính nó. Khái niệm đồ thị trong lý thuyết đồ thị dựa trên một số thuật ngữ cơ bản như điểm, đường thẳng, đỉnh, cạnh, tung độ của đỉnh, các tính chất của đồ thị, ... Ở đây, trong chương này, chúng ta sẽ trình bày những điều cơ bản của lý thuyết đồ thị.

Điểm

A pointlà một vị trí cụ thể trong không gian một chiều, hai chiều hoặc ba chiều. Để hiểu rõ hơn, một điểm có thể được biểu thị bằng một bảng chữ cái. Nó có thể được biểu thị bằng một dấu chấm.

Thí dụ

Ở đây, dấu chấm là một điểm có tên là 'a'.

Hàng

A Linelà sự kết nối giữa hai điểm. Nó có thể được biểu diễn bằng một đường liền nét.

Example

Ở đây, 'a' và 'b' là các điểm. Liên kết giữa hai điểm này được gọi là một đoạn thẳng.

Đỉnh

Đỉnh là một điểm mà nhiều đường gặp nhau. Nó còn được gọi lànode. Tương tự như điểm, một đỉnh cũng được ký hiệu bằng bảng chữ cái.

Example

Ở đây, đỉnh được đặt tên bằng bảng chữ cái 'a'.

Cạnh

Một cạnh là một thuật ngữ toán học để chỉ một đoạn thẳng nối hai đỉnh. Nhiều cạnh có thể được hình thành từ một đỉnh duy nhất. Không có đỉnh thì không thể hình thành cạnh. Phải có một đỉnh bắt đầu và một đỉnh kết thúc cho một cạnh.

Example

Ở đây, 'a' và 'b' là hai đỉnh và liên kết giữa chúng được gọi là cạnh.

Đồ thị

Đồ thị 'G' được định nghĩa là G = (V, E) Trong đó V là tập hợp tất cả các đỉnh và E là tập hợp tất cả các cạnh trong đồ thị.

Example 1

Trong ví dụ trên, ab, ac, cd và bd là các cạnh của đồ thị. Tương tự, a, b, c và d là các đỉnh của đồ thị.

Example 2

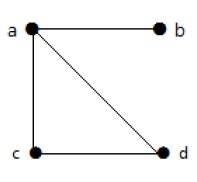
Trong đồ thị này, có bốn đỉnh a, b, c, d và bốn cạnh ab, ac, ad và cd.

Vòng

Trong một đồ thị, nếu một cạnh được vẽ từ đỉnh đến chính nó, nó được gọi là một vòng lặp.

Example 1

Trong đồ thị trên, V là đỉnh mà nó có cạnh (V, V) tạo thành một đường tròn.

Example 2

Trong đồ thị này, có hai vòng lặp được tạo thành ở đỉnh a và đỉnh b.

Mức độ của Vertex

Nó là số đỉnh kề với đỉnh V.

Notation - độ (V).

Trong một đồ thị đơn giản với n số đỉnh, tung độ của bất kỳ đỉnh nào là -

deg (v) ≤ n - 1 ∀ v ∈ G

Một đỉnh có thể tạo thành một cạnh với tất cả các đỉnh khác ngoại trừ chính nó. Vì vậy, mức độ của một đỉnh sẽ lên đếnnumber of vertices in the graph minus 1. Số 1 này dành cho đỉnh tự vì nó không thể tự tạo thành một vòng lặp. Nếu có một vòng lặp tại bất kỳ đỉnh nào, thì đó không phải là một Đồ thị Đơn giản.

Độ của đỉnh có thể được xem xét theo hai trường hợp của đồ thị:

Đồ thị vô hướng
Đồ thị hướng

Mức độ của đỉnh trong một đồ thị vô hướng

Một đồ thị vô hướng không có các cạnh có hướng. Hãy xem xét các ví dụ sau.

Example 1

Hãy xem biểu đồ sau:

Trong Đồ thị vô hướng ở trên,

deg (a) = 2, vì có 2 cạnh gặp nhau tại đỉnh 'a'.
deg (b) = 3, vì có 3 cạnh gặp nhau tại đỉnh 'b'.
deg (c) = 1, vì có 1 cạnh được tạo thành ở đỉnh 'c'
Vì vậy, 'c' là một pendent vertex.
deg (d) = 2, vì có 2 cạnh gặp nhau tại đỉnh 'd'.
deg (e) = 0, vì có 0 cạnh được tạo thành ở đỉnh 'e'.
Vì vậy, 'e' là một isolated vertex.

Example 2

Hãy xem biểu đồ sau:

Trong biểu đồ trên,

deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 và deg (e) = 0.

Đỉnh 'e' là một đỉnh cô lập. Đồ thị không có bất kỳ đỉnh nào.

Mức độ của đỉnh trong đồ thị có hướng

Trong một đồ thị có hướng, mỗi đỉnh có một indegree và một outdegree.

Không giới hạn của một đồ thị

Không giới hạn của đỉnh V là số cạnh đi vào đỉnh V.
Notation - deg− (V).

Vượt trội của một đồ thị

Số dư của đỉnh V là số cạnh đi ra khỏi đỉnh V.
Notation - deg + (V).

Hãy xem xét các ví dụ sau.

Example 1

Hãy xem biểu đồ hướng dẫn sau. Đỉnh 'a' có hai cạnh, 'ad' và 'ab', hướng ra ngoài. Do đó độ lớn của nó là 2. Tương tự, có một cạnh 'ga', hướng tới đỉnh 'a'. Do đó, hàm số 'a' là 1.

Điểm vượt trội và vượt trội của các đỉnh khác được thể hiện trong bảng sau:

Đỉnh	Thời gian	Outdegree
a	1	2
b	2	0
c	2	1
d	1	1
e	1	1
f	1	1
g	0	2

Example 2

Hãy xem biểu đồ hướng dẫn sau. Đỉnh 'a' có một cạnh 'ae' đi ra ngoài từ đỉnh 'a'. Do đó, độ lớn của nó là 1. Tương tự, đồ thị có một cạnh 'ba' hướng tới đỉnh 'a'. Do đó, hàm số 'a' là 1.

Điểm vượt trội và vượt trội của các đỉnh khác được thể hiện trong bảng sau:

Đỉnh	Thời gian	Outdegree
a	1	1
b	0	2
c	2	0
d	1	1
e	1	1

Pendent Vertex

Bằng cách sử dụng bậc của một đỉnh, chúng ta có hai loại đỉnh đặc biệt. Một đỉnh có bậc một được gọi là một đỉnh mặt nghiêng.

Example

Ở đây, trong ví dụ này, đỉnh 'a' và đỉnh 'b' có cạnh nối là 'ab'. Vì vậy đối với đỉnh 'a', chỉ có một cạnh đối với đỉnh 'b' và tương tự đối với đỉnh 'b', chỉ có một cạnh đối với đỉnh 'a'. Cuối cùng, đỉnh 'a' và đỉnh 'b' có tung độ là một, còn được gọi là đỉnh mặt nghiêng.

Đỉnh cô lập

Đỉnh có tung độ bằng 0 được gọi là đỉnh cô lập.

Example

Ở đây, đỉnh 'a' và đỉnh 'b' không có mối liên hệ nào giữa nhau và với bất kỳ đỉnh nào khác. Vậy tung độ của cả hai đỉnh 'a' và 'b' đều bằng không. Đây cũng được gọi là các đỉnh cô lập.

Sự gần gũi

Dưới đây là các tiêu chuẩn của sự gần kề -

Trong một đồ thị, hai đỉnh được cho là adjacent, nếu có một cạnh giữa hai đỉnh. Ở đây, cạnh kề của các đỉnh được duy trì bởi một cạnh duy nhất nối hai đỉnh đó.
Trong một đồ thị, hai cạnh được cho là kề nhau, nếu có một đỉnh chung giữa hai cạnh. Ở đây, cạnh kề của các cạnh được duy trì bởi một đỉnh duy nhất nối hai cạnh.

Example 1

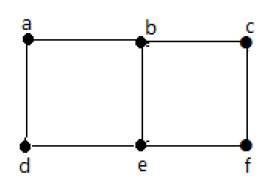
Trong biểu đồ trên -

'a' và 'b' là các đỉnh liền kề, vì có một cạnh chung 'ab' giữa chúng.
'a' và 'd' là các đỉnh liền kề, vì có một cạnh chung 'ad' giữa chúng.
ab 'và' be 'là các cạnh liền kề vì có một đỉnh chung' b 'giữa chúng.
be 'và' de 'là các cạnh liền kề, vì có một đỉnh chung' e 'giữa chúng.

Example 2

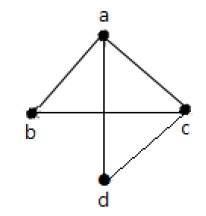
Trong biểu đồ trên -

'a' và 'd' là các đỉnh liền kề, vì có một cạnh chung 'ad' giữa chúng.
'c' và 'b' là các đỉnh liền kề, vì có một cạnh chung 'cb' giữa chúng.
'ad' và 'cd' là các cạnh liền kề, vì có một đỉnh chung 'd' giữa chúng.
'ac' và 'cd' là các cạnh liền kề, vì có một đỉnh chung 'c' giữa chúng.

Cạnh song song

Trong đồ thị, nếu một cặp đỉnh được nối bởi nhiều hơn một cạnh thì các cạnh đó được gọi là các cạnh song song.

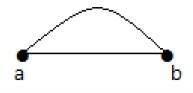
Trong đồ thị trên, 'a' và 'b' là hai đỉnh được nối bởi hai cạnh 'ab' và 'ab' giữa chúng. Vì vậy nó được gọi là cạnh song song.

Đa đồ thị

Đồ thị có các cạnh song song được gọi là Đồ thị đa dạng.

Example 1

Trong đồ thị trên, có năm cạnh 'ab', 'ac', 'cd', 'cd' và 'bd'. Vì 'c' và 'd' có hai cạnh song song giữa chúng nên nó là một Multigraph.

Example 2

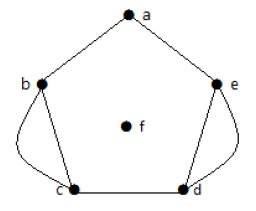
Trong đồ thị trên, các đỉnh 'b' và 'c' có hai cạnh. Các đỉnh 'e' và 'd' cũng có hai cạnh giữa chúng. Do đó nó là một Multigraph.

Trình tự mức độ của một đồ thị

Nếu bậc của tất cả các đỉnh trong đồ thị được sắp xếp theo thứ tự giảm dần hoặc tăng dần, thì dãy thu được được gọi là dãy bậc của đồ thị.

Example 1

Đỉnh	A	b	c	d	e
Đang kết nối tới	b, c	a, d	a, d	c, b, e	d
Trình độ	2	2	2	3	1

Trong đồ thị trên, đối với các đỉnh {d, a, b, c, e}, thứ tự bậc là {3, 2, 2, 2, 1}.

Example 2

Đỉnh	A	b	c	d	e	f
Đang kết nối tới	là	AC	b, d	c, e	a, d	-
Trình độ	2	2	2	2	2	0

Trong đồ thị trên, đối với các đỉnh {a, b, c, d, e, f}, bậc là {2, 2, 2, 2, 2, 0}.