Lý thuyết đồ thị - Cây
Cây cối là đồ thị không chứa dù chỉ một chu trình. Chúng thể hiện cấu trúc phân cấp dưới dạng đồ họa. Cây cối thuộc loại đồ thị đơn giản nhất. Mặc dù đơn giản nhưng chúng có cấu trúc phong phú.
Cây cung cấp một loạt các ứng dụng hữu ích từ đơn giản như cây gia đình đến phức tạp như cây trong cấu trúc dữ liệu của khoa học máy tính.
Cây
A connected acyclic graphđược gọi là cây. Nói cách khác, một đồ thị liên thông không có chu trình được gọi là cây.
Các cạnh của cây được gọi là branches. Các phần tử của cây được gọi là nút của chúng. Các nút không có nút con được gọi làleaf nodes.
Một cây có 'n' đỉnh có 'n-1' cạnh. Nếu nó có nhiều cạnh hơn 'n-1', thì cạnh thừa rõ ràng phải ghép nối với hai đỉnh để tạo thành một chu trình. Sau đó, nó trở thành một đồ thị theo chu kỳ, điều này là vi phạm đối với đồ thị dạng cây.
Example 1
Biểu đồ được hiển thị ở đây là một cái cây vì nó không có chu trình và nó được kết nối với nhau. Nó có bốn đỉnh và ba cạnh, tức là đối với 'n' các cạnh 'n-1' như đã đề cập trong định nghĩa.
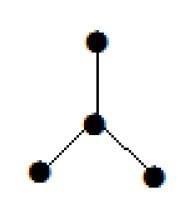
Note - Cây nào cũng có ít nhất hai đỉnh bậc một.
Example 2
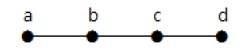
Trong ví dụ trên, các đỉnh 'a' và 'd' có bậc một. Và hai đỉnh còn lại 'b' và 'c' có bậc hai. Điều này có thể xảy ra vì để không tạo thành một chu trình, nên có ít nhất hai cạnh đơn ở bất kỳ đâu trong đồ thị. Nó không là gì ngoài hai cạnh với mức độ bằng một.
rừng
A disconnected acyclic graphđược gọi là rừng. Nói cách khác, một tập hợp cây rời rạc được gọi là rừng.
Example
Đồ thị sau đây giống như hai đồ thị con; nhưng nó là một đồ thị bị ngắt kết nối duy nhất. Không có chu trình nào trong đồ thị này. Do đó, rõ ràng đó là một khu rừng.
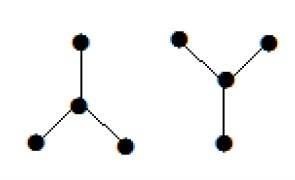
Cây kéo dài
Gọi G là một đồ thị liên thông, khi đó đồ thị con H của G được gọi là cây khung của G nếu -
- H là cây
- H chứa tất cả các đỉnh của G.
Cây bao trùm T của đồ thị vô hướng G là một đồ thị con bao gồm tất cả các đỉnh của G.
Example

Trong ví dụ trên, G là một đồ thị liên thông và H là một đồ thị con của G.
Rõ ràng, đồ thị H không có chu trình, nó là một cây có sáu cạnh nhỏ hơn tổng số đỉnh là một. Do đó H là cây Spanning của G.
Xếp hạng mạch
Gọi 'G' là một đồ thị liên thông với 'n' đỉnh và 'm' cạnh. Cây bao trùm 'T' của G chứa (n-1) cạnh.
Do đó, số cạnh bạn cần xóa khỏi 'G' để có được cây khung = m- (n-1), được gọi là bậc mạch của G.
Công thức này đúng, bởi vì trong cây khung, bạn cần có 'n-1' cạnh. Ngoài các cạnh 'm', bạn cần giữ lại các cạnh 'n – 1' trong biểu đồ.
Do đó, việc xóa các cạnh 'n – 1' khỏi 'm' sẽ cho các cạnh bị xóa khỏi đồ thị để có được cây khung, cây không nên tạo thành một chu trình.
Example
Hãy xem biểu đồ sau:
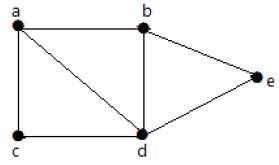
Đối với đồ thị cho trong ví dụ trên, bạn có m = 7 cạnh và n = 5 đỉnh.
Khi đó thứ hạng của mạch là -
Example
Gọi 'G' là một đồ thị liên thông với sáu đỉnh và tung độ của mỗi đỉnh là ba. Tìm hạng mạch của 'G'.
Theo định lý tổng bậc của các đỉnh,
Định lý Kirchoff
Định lý Kirchoff rất hữu ích trong việc tìm số cây khung có thể được hình thành từ một đồ thị liên thông.
Example
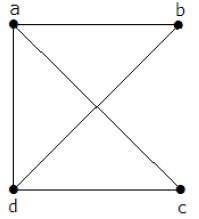
Ma trận 'A' được điền như, nếu có một cạnh giữa hai đỉnh, thì nó sẽ được cho là '1', khác là '0'.
$$ A = \ begin {vmatrix} 0 & a & b & c & d \\ a & 0 & 1 & 1 & 1 \\ b & 1 & 0 & 0 & 1 \\ c & 1 & 0 & 0 & 1 \\ d & 1 & 1 & 1 & 0 \ end {vmatrix} = \ begin {vmatrix} 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \ end {vmatrix} $$Bằng cách sử dụng định lý kirchoff, nó sẽ được thay đổi như thay thế các giá trị đường chéo nguyên tắc bằng mức độ của các đỉnh và tất cả các phần tử khác bằng -1.A
$$ = \ begin {vmatrix} 3 & -1 & -1 & -1 \\ - 1 & 2 & 0 & -1 \\ - 1 & 0 & 2 & -1 \\ - 1 & -1 & -1 & 3 \ end {vmatrix} = M $$ $$ M = \ begin {vmatrix} 3 & -1 & -1 & -1 \\ - 1 & 2 & 0 & -1 \\ - 1 & 0 & 2 & -1 \\ - 1 & -1 & -1 & 3 \ end {vmatrix} = 8 $$ $$ Co \: \: factor \: \: of \: \: m1 \: \: = \ begin {vmatrix } 2 & 0 & -1 \\ 0 & 2 & -1 \\ - 1 & -1 & 3 \ end {vmatrix} $$Như vậy, số cây khung = 8.