Lý thuyết đồ thị - Hướng dẫn nhanh

Trong lĩnh vực toán học và khoa học máy tính, lý thuyết đồ thị là nghiên cứu về đồ thị liên quan đến mối quan hệ giữa các cạnh và đỉnh . Nó là một chủ đề phổ biến có các ứng dụng của nó trong khoa học máy tính, công nghệ thông tin, khoa học sinh học, toán học và ngôn ngữ học. Nếu không cần thêm gì nữa, chúng ta hãy bắt đầu với việc xác định một biểu đồ.

Đồ thị là gì?

Đồ thị là một biểu diễn bằng hình ảnh của một tập hợp các đối tượng trong đó một số cặp đối tượng được nối với nhau bằng các liên kết. Các đối tượng được kết nối với nhau được biểu diễn bằng các điểm được gọi làverticesvà các liên kết nối các đỉnh được gọi là edges.

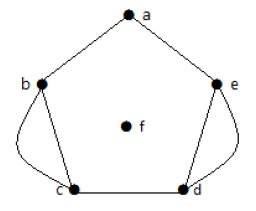
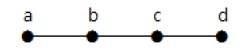
Về mặt hình thức, biểu đồ là một cặp tập hợp (V, E), Ở đâu Vlà tập các đỉnh và E là tập các cạnh, nối các cặp đỉnh. Hãy xem biểu đồ sau:

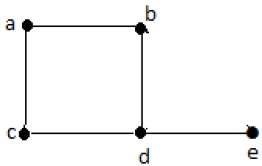
Trong biểu đồ trên,

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

Các ứng dụng của lý thuyết đồ thị

Lý thuyết đồ thị có các ứng dụng của nó trong các lĩnh vực kỹ thuật đa dạng -

Electrical Engineering- Các khái niệm của lý thuyết đồ thị được sử dụng nhiều trong việc thiết kế các kết nối mạch. Các loại hoặc tổ chức của kết nối được đặt tên là cấu trúc liên kết. Một số ví dụ cho cấu trúc liên kết là cấu trúc liên kết hình sao, cầu, chuỗi và song song.

Computer Science- Lý thuyết đồ thị được sử dụng để nghiên cứu các thuật toán. Ví dụ,

• Thuật toán Kruskal
• Thuật toán của Prim
• Thuật toán Dijkstra

Computer Network - Các mối quan hệ giữa các máy tính kết nối với nhau trong mạng tuân theo các nguyên tắc của lý thuyết đồ thị.

Science - Cấu trúc phân tử và cấu trúc hóa học của một chất, cấu trúc ADN của sinh vật, ... được biểu diễn bằng biểu đồ.

Linguistics - Cây phân tích cú pháp của một ngôn ngữ và ngữ pháp của một ngôn ngữ sử dụng biểu đồ.

General- Các tuyến đường giữa các thành phố có thể được biểu diễn bằng biểu đồ. Mô tả thông tin có thứ tự thứ bậc như cây gia đình có thể được sử dụng như một loại biểu đồ đặc biệt được gọi là cây.

Đồ thị là một biểu đồ gồm các điểm và các đường thẳng nối với các điểm. Nó có ít nhất một dòng nối một tập hợp hai đỉnh mà không có đỉnh nào nối chính nó. Khái niệm đồ thị trong lý thuyết đồ thị dựa trên một số thuật ngữ cơ bản như điểm, đường thẳng, đỉnh, cạnh, tung độ của đỉnh, các tính chất của đồ thị, ... Ở đây, trong chương này, chúng ta sẽ trình bày những điều cơ bản của lý thuyết đồ thị.

Điểm

A pointlà một vị trí cụ thể trong không gian một chiều, hai chiều hoặc ba chiều. Để hiểu rõ hơn, một điểm có thể được biểu thị bằng một bảng chữ cái. Nó có thể được biểu thị bằng một dấu chấm.

Thí dụ

Ở đây, dấu chấm là một điểm có tên là 'a'.

Hàng

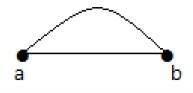
A Linelà một kết nối giữa hai điểm. Nó có thể được biểu diễn bằng một đường liền nét.

Example

Ở đây, 'a' và 'b' là các điểm. Liên kết giữa hai điểm này được gọi là đường thẳng.

Đỉnh

Đỉnh là một điểm mà nhiều đường thẳng gặp nhau. Nó còn được gọi lànode. Tương tự như điểm, một đỉnh cũng được ký hiệu bằng bảng chữ cái.

Example

Ở đây, đỉnh được đặt tên bằng bảng chữ cái 'a'.

Cạnh

Cạnh là một thuật ngữ toán học để chỉ một đường nối hai đỉnh. Nhiều cạnh có thể được hình thành từ một đỉnh duy nhất. Không có đỉnh thì không thể hình thành cạnh. Phải có một đỉnh bắt đầu và một đỉnh kết thúc cho một cạnh.

Example

Ở đây, 'a' và 'b' là hai đỉnh và liên kết giữa chúng được gọi là cạnh.

Đồ thị

Đồ thị 'G' được định nghĩa là G = (V, E) Trong đó V là tập hợp tất cả các đỉnh và E là tập hợp tất cả các cạnh trong đồ thị.

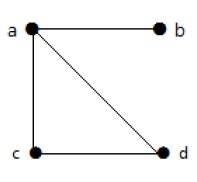
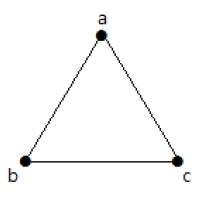
Example 1

Trong ví dụ trên, ab, ac, cd và bd là các cạnh của đồ thị. Tương tự, a, b, c và d là các đỉnh của đồ thị.

Example 2

Trong đồ thị này, có bốn đỉnh a, b, c, d và bốn cạnh ab, ac, ad và cd.

Vòng

Trong một đồ thị, nếu một cạnh được vẽ từ đỉnh đến chính nó, nó được gọi là một vòng lặp.

Example 1

Trong đồ thị trên, V là một đỉnh mà nó có cạnh (V, V) tạo thành một đường tròn.

Example 2

Trong đồ thị này, có hai vòng lặp được tạo thành ở đỉnh a và đỉnh b.

Mức độ của Vertex

Nó là số đỉnh kề với đỉnh V.

Notation - độ (V).

Trong một đồ thị đơn giản với n số đỉnh, tung độ của bất kỳ đỉnh nào là:

deg (v) ≤ n - 1 ∀ v ∈ G

Một đỉnh có thể tạo thành một cạnh với tất cả các đỉnh khác ngoại trừ chính nó. Vì vậy, mức độ của một đỉnh sẽ lên đếnnumber of vertices in the graph minus 1. Giá trị 1 này dành cho đỉnh tự vì nó không thể tự tạo thành một vòng lặp. Nếu có một vòng lặp tại bất kỳ đỉnh nào, thì nó không phải là một Đồ thị Đơn giản.

Độ của đỉnh có thể được xem xét theo hai trường hợp của đồ thị:

• Đồ thị vô hướng

• Đồ thị hướng

Mức độ của đỉnh trong một đồ thị vô hướng

Một đồ thị vô hướng không có các cạnh có hướng. Hãy xem xét các ví dụ sau.

Example 1

Hãy xem biểu đồ sau:

Trong Đồ thị vô hướng ở trên,

• deg (a) = 2, vì có 2 cạnh gặp nhau tại đỉnh 'a'.

• deg (b) = 3, vì có 3 cạnh gặp nhau tại đỉnh 'b'.

• deg (c) = 1, vì có 1 cạnh được tạo thành ở đỉnh 'c'

• Vì vậy, 'c' là một pendent vertex.

• deg (d) = 2, vì có 2 cạnh gặp nhau tại đỉnh 'd'.

• deg (e) = 0, vì có 0 cạnh được tạo thành ở đỉnh 'e'.

• Vì vậy, 'e' là một isolated vertex.

Example 2

Hãy xem biểu đồ sau:

Trong biểu đồ trên,

deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 và deg (e) = 0.

Đỉnh 'e' là một đỉnh cô lập. Đồ thị không có bất kỳ đỉnh nào.

Mức độ của đỉnh trong đồ thị có hướng

Trong một đồ thị có hướng, mỗi đỉnh có một indegree và một outdegree.

Không giới hạn của một đồ thị

• Không giới hạn của đỉnh V là số cạnh đi vào đỉnh V.

• Notation - deg− (V).

Vượt trội của một đồ thị

• Độ lớn của đỉnh V là số cạnh đi ra khỏi đỉnh V.

• Notation - deg + (V).

Hãy xem xét các ví dụ sau.

Example 1

Hãy xem biểu đồ hướng dẫn sau đây. Đỉnh 'a' có hai cạnh, 'ad' và 'ab', hướng ra ngoài. Do đó, độ lớn của nó là 2. Tương tự, có một cạnh 'ga', hướng tới đỉnh 'a'. Do đó, hàm số 'a' là 1.

Điểm vượt trội và vượt trội của các đỉnh khác được thể hiện trong bảng sau:

Đỉnh	Thời gian	Outdegree
a	1	2
b	2	0
c	2	1
d	1	1
e	1	1
f	1	1
g	0	2

Example 2

Hãy xem biểu đồ hướng dẫn sau đây. Đỉnh 'a' có một cạnh 'ae' đi ra ngoài từ đỉnh 'a'. Do đó, độ lớn của nó là 1. Tương tự, đồ thị có cạnh 'ba' hướng tới đỉnh 'a'. Do đó, hàm số 'a' là 1.

Điểm vượt trội và vượt trội của các đỉnh khác được thể hiện trong bảng sau:

Đỉnh	Thời gian	Outdegree
a	1	1
b	0	2
c	2	0
d	1	1
e	1	1

Pendent Vertex

Bằng cách sử dụng bậc của một đỉnh, chúng ta có hai loại đỉnh đặc biệt. Đỉnh có bậc một được gọi là đỉnh mặt nghiêng.

Example

Ở đây, trong ví dụ này, đỉnh 'a' và đỉnh 'b' có cạnh nối là 'ab'. Vì vậy đối với đỉnh 'a', chỉ có một cạnh đối với đỉnh 'b' và tương tự đối với đỉnh 'b', chỉ có một cạnh đối với đỉnh 'a'. Cuối cùng, đỉnh 'a' và đỉnh 'b' có tung độ là một, còn được gọi là đỉnh mặt nghiêng.

Đỉnh cô lập

Đỉnh có tung độ bằng 0 được gọi là đỉnh cô lập.

Example

Ở đây, đỉnh 'a' và đỉnh 'b' không có mối liên hệ nào giữa nhau và với bất kỳ đỉnh nào khác. Vậy tung độ của cả hai đỉnh 'a' và 'b' đều bằng không. Đây cũng được gọi là các đỉnh cô lập.

Sự gần gũi

Dưới đây là các tiêu chuẩn của sự gần kề -

• Trong một đồ thị, hai đỉnh được cho là adjacent, nếu có một cạnh giữa hai đỉnh. Ở đây, cạnh kề của các đỉnh được duy trì bởi một cạnh duy nhất nối hai đỉnh đó.

• Trong một đồ thị, hai cạnh được cho là kề nhau, nếu có một đỉnh chung giữa hai cạnh. Ở đây, cạnh kề của các cạnh được duy trì bởi một đỉnh duy nhất nối hai cạnh.

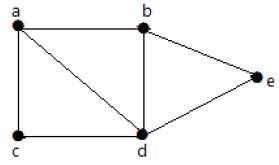
Example 1

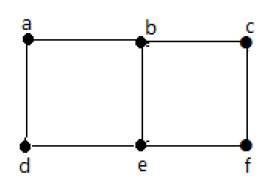
Trong biểu đồ trên -

• 'a' và 'b' là các đỉnh liền kề, vì có một cạnh chung 'ab' giữa chúng.

• 'a' và 'd' là các đỉnh liền kề, vì có một cạnh chung 'ad' giữa chúng.

• ab 'và' be 'là các cạnh liền kề, vì có một đỉnh chung' b 'giữa chúng.

• be 'và' de 'là các cạnh liền kề, vì có một đỉnh chung' e 'giữa chúng.

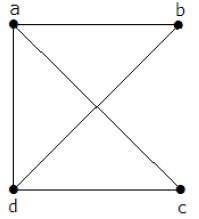
Example 2

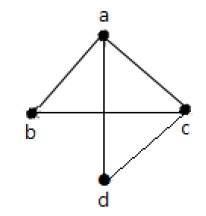
Trong biểu đồ trên -

• 'a' và 'd' là các đỉnh liền kề, vì có một cạnh chung 'ad' giữa chúng.

• 'c' và 'b' là các đỉnh liền kề, vì có một cạnh chung 'cb' giữa chúng.

• 'ad' và 'cd' là các cạnh liền kề, vì có một đỉnh chung 'd' giữa chúng.

• 'ac' và 'cd' là các cạnh liền kề, vì có một đỉnh chung 'c' giữa chúng.

Cạnh song song

Trong một đồ thị, nếu một cặp đỉnh được nối bởi nhiều hơn một cạnh thì các cạnh đó được gọi là các cạnh song song.

Trong đồ thị trên, 'a' và 'b' là hai đỉnh được nối bởi hai cạnh 'ab' và 'ab' giữa chúng. Vì vậy nó được gọi là cạnh song song.

Đa đồ thị

Đồ thị có các cạnh song song được gọi là Đồ thị đa dạng.

Example 1

Trong đồ thị trên, có năm cạnh 'ab', 'ac', 'cd', 'cd' và 'bd'. Vì 'c' và 'd' có hai cạnh song song giữa chúng nên nó là một Multigraph.

Example 2

Trong đồ thị trên, các đỉnh 'b' và 'c' có hai cạnh. Các đỉnh 'e' và 'd' cũng có hai cạnh giữa chúng. Do đó nó là một Multigraph.

Trình tự mức độ của một đồ thị

Nếu bậc của tất cả các đỉnh trong đồ thị được sắp xếp theo thứ tự giảm dần hoặc tăng dần, thì dãy thu được được gọi là dãy bậc của đồ thị.

Example 1

Đỉnh	A	b	c	d	e
Đang kết nối tới	b, c	a, d	a, d	c, b, e	d
Trình độ	2	2	2	3	1

Trong đồ thị trên, đối với các đỉnh {d, a, b, c, e}, bậc là {3, 2, 2, 2, 1}.

Example 2

Đỉnh	A	b	c	d	e	f
Đang kết nối tới	là	AC	b, d	c, e	a, d	-
Trình độ	2	2	2	2	2	0

Trong đồ thị trên, đối với các đỉnh {a, b, c, d, e, f}, bậc là {2, 2, 2, 2, 2, 0}.

Đồ thị có các thuộc tính khác nhau được sử dụng để mô tả đặc điểm của đồ thị tùy thuộc vào cấu trúc của chúng. Các thuộc tính này được định nghĩa theo các thuật ngữ cụ thể liên quan đến lĩnh vực lý thuyết đồ thị. Trong chương này, chúng ta sẽ thảo luận về một vài tính chất cơ bản phổ biến trong tất cả các đồ thị.

Khoảng cách giữa hai đỉnh

Nó là số cạnh trên đường đi ngắn nhất giữa đỉnh U và đỉnh V. Nếu có nhiều đường nối hai đỉnh thì đường đi ngắn nhất được coi là khoảng cách giữa hai đỉnh.

Kí hiệu - d (U, V)

Có thể có bất kỳ số lượng đường đi nào từ đỉnh này đến đỉnh khác. Trong số đó, bạn chỉ cần chọn một cái ngắn nhất.

Example

Hãy xem biểu đồ sau:

Ở đây, khoảng cách từ đỉnh 'd' đến đỉnh 'e' hay đơn giản là 'de' là 1 vì có một cạnh giữa chúng. Có nhiều đường đi từ đỉnh 'd' đến đỉnh 'e' -

• da, ab, be
• df, fg, ge
• de (Nó được coi là khoảng cách giữa các đỉnh)
• df, fc, ca, ab, be
• da, ac, cf, fg, ge

Độ lệch tâm của đỉnh

Khoảng cách lớn nhất giữa một đỉnh với tất cả các đỉnh khác được coi là độ lệch tâm của đỉnh.

Kí hiệu - e (V)

Khoảng cách từ một đỉnh cụ thể đến tất cả các đỉnh khác trong đồ thị được lấy và trong số các khoảng cách đó, độ lệch tâm là khoảng cách cao nhất.

Example

Trong đồ thị trên, độ lệch tâm của 'a' là 3.

Khoảng cách từ 'a' đến 'b' là 1 ('ab'),

từ 'a' đến 'c' là 1 ('ac'),

từ 'a' đến 'd' là 1 ('ad'),

từ 'a' đến 'e' là 2 ('ab' - 'be') hoặc ('ad' - 'de'),

từ 'a' đến 'f' là 2 ('ac' - 'cf') hoặc ('ad' - 'df'),

từ 'a' đến 'g' là 3 ('ac' - 'cf' - 'fg') hoặc ('ad' - 'df' - 'fg').

Vì vậy, độ lệch tâm là 3, là cực đại từ đỉnh 'a' và khoảng cách giữa 'ag' là cực đại.

Nói cách khác,

e (b) = 3

e (c) = 3

e (d) = 2

e (e) = 3

e (f) = 3

e (g) = 3

Bán kính của một đồ thị được kết nối

Độ lệch tâm nhỏ nhất từ ​​tất cả các đỉnh được coi là bán kính của Đồ thị G. Giá trị nhỏ nhất trong số tất cả các khoảng cách lớn nhất giữa một đỉnh với tất cả các đỉnh khác được coi là bán kính của Đồ thị G.

Kí hiệu - r (G)

Từ tất cả các độ lệch tâm của các đỉnh trong một đồ thị, bán kính của đồ thị liên thông là giá trị nhỏ nhất của tất cả các độ lệch tâm đó.

Example

Trong đồ thị trên, r (G) = 2, là độ lệch tâm nhỏ nhất của 'd'.

Đường kính của một đồ thị

Độ lệch tâm lớn nhất từ ​​tất cả các đỉnh được coi là đường kính của Đồ thị G. Giá trị lớn nhất trong số tất cả các khoảng cách giữa một đỉnh đến tất cả các đỉnh khác được coi là đường kính của Đồ thị G.

Notation − d(G) - Từ tất cả các độ lệch tâm của các đỉnh trong một đồ thị, đường kính của đồ thị liên thông là cực đại của tất cả các đường lệch tâm đó.

Example

Trong đồ thị trên, d (G) = 3; là độ lệch tâm lớn nhất.

Tâm điểm

Nếu độ lệch tâm của một đồ thị bằng với bán kính của nó, thì nó được gọi là điểm chính giữa của đồ thị. Nếu

e (V) = r (V),

thì 'V' là điểm chính giữa của Đồ thị 'G'.

Example

Trong đồ thị ví dụ, 'd' là điểm chính giữa của đồ thị.

e (d) = r (d) = 2

Trung tâm

Tập hợp tất cả các điểm chính giữa của 'G' được gọi là trọng tâm của Đồ thị.

Example

Trong biểu đồ ví dụ, {'d'} là tâm của Biểu đồ.

Chu vi

Các number of edges in the longest cycle of ‘G’ được gọi là chu vi của 'G'.

Example

Trong biểu đồ ví dụ, chu vi là 6, mà chúng tôi suy ra từ chu kỳ dài nhất acfgeba hoặc acfdeba.

Đường tròn

Số cạnh trong chu kỳ ngắn nhất của 'G' được gọi là Girth của nó.

Notation: g (G).

Example - Trong đồ thị ví dụ, Girth của đồ thị là 4, chúng ta suy ra từ chu trình ngắn nhất acfda hoặc dfged hoặc abeda.

Định lý tổng bậc của các đỉnh

Nếu G = (V, E) là một đồ thị không có hướng với các đỉnh V = {V ₁ , V ₂ ,… V _n } thì

n Σ i = 1 deg (V _i ) = 2 | E |

Corollary 1

Nếu G = (V, E) là một đồ thị có hướng với các đỉnh V = {V ₁ , V ₂ ,… V _n } thì

n Σ i = 1 deg + (V _i ) = | E | = n Σ i = 1 deg− (V _i )

Corollary 2

Trong bất kỳ đồ thị không hướng nào, số đỉnh có bậc Lẻ là Chẵn.

Corollary 3

Trong đồ thị không có hướng, nếu tung độ của mỗi đỉnh là k, thì

k | V | = 2 | E |

Corollary 4

Trong đồ thị không có hướng, nếu tung độ của mỗi đỉnh ít nhất là k, thì

k | V | ≤ 2 | E |

| Corollary 5

Trong đồ thị không có hướng, nếu tung độ của mỗi đỉnh nhiều nhất là k, thì

k | V | ≥ 2 | E |

Có nhiều loại đồ thị khác nhau tùy thuộc vào số lượng đỉnh, số cạnh, liên kết và cấu trúc tổng thể của chúng. Chúng ta sẽ chỉ thảo luận một số dạng đồ thị quan trọng nhất định trong chương này.

Đồ thị rỗng

A graph having no edges được gọi là Đồ thị rỗng.

Thí dụ

Trong đồ thị trên, có ba đỉnh được đặt tên là 'a', 'b' và 'c', nhưng không có cạnh nào trong số chúng. Do đó, nó là một Đồ thị rỗng.

Đồ thị tầm thường

A graph with only one vertex được gọi là Đồ thị tầm thường.

Thí dụ

Trong đồ thị trên, chỉ có một đỉnh 'a' không có cạnh nào khác. Do đó, nó là một đồ thị tầm thường.

Đồ thị không hướng

Một đồ thị không có hướng chứa các cạnh nhưng các cạnh không có hướng.

Thí dụ

Trong biểu đồ này, 'a', 'b', 'c', 'd', 'e', ​​'f', 'g' là các đỉnh và 'ab', 'bc', 'cd', 'da ',' ag ',' gf ',' ef 'là các cạnh của đồ thị. Vì nó là một đồ thị không có hướng nên các cạnh 'ab' và 'ba' giống nhau. Tương tự các cạnh khác cũng xét theo cách tương tự.

Đồ thị hướng

Trong một đồ thị có hướng, mỗi cạnh có một hướng.

Thí dụ

Trong đồ thị trên, chúng ta có bảy đỉnh 'a', 'b', 'c', 'd', 'e', ​​'f', và 'g', và tám cạnh 'ab', 'cb', ' dc ',' ad ',' ec ',' fe ',' gf 'và' ga '. Vì nó là một đồ thị có hướng, mỗi cạnh có một dấu mũi tên cho biết hướng của nó. Lưu ý rằng trong đồ thị có hướng, 'ab' khác với 'ba'.

Đồ thị đơn giản

Một đồ thị with no loops và không parallel edges được gọi là một đồ thị đơn giản.

• Số cạnh lớn nhất có thể có trong một đồ thị có 'n' đỉnh là ⁿ C ₂ trong đó ⁿ C ₂ = n (n - 1) / 2.

• Số lượng đồ thị đơn giản có thể có 'n' đỉnh = 2 _{ⁿ c 2} = 2 ^{n (n-1) / 2} .

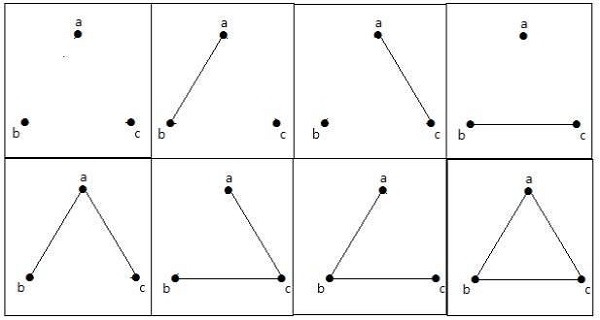
Thí dụ

Trong đồ thị sau có 3 đỉnh có 3 cạnh là cực đại không kể cạnh và đường tròn song song. Điều này có thể được chứng minh bằng cách sử dụng các công thức trên.

Số cạnh lớn nhất có n = 3 đỉnh -

ⁿ C ₂ = n (n – 1) / 2

= 3 (3–1) / 2

= 6/2

= 3 cạnh

Số lượng đồ thị đơn giản tối đa có n = 3 đỉnh -

2 _{ⁿ C 2} = 2 ^{n (n-1) / 2}

= 2 ^{3 (3-1) / 2}

= 2 ³

số 8

8 đồ thị này như hình dưới đây -

Biểu đồ được kết nối

Một đồ thị G được cho là liên kết if there exists a path between every pair of vertices. Nên có ít nhất một cạnh cho mọi đỉnh trong đồ thị. Vì vậy, chúng ta có thể nói rằng nó được kết nối với một số đỉnh khác ở phía bên kia của cạnh.

Thí dụ

Trong đồ thị sau, mỗi đỉnh có cạnh riêng của nó nối với cạnh khác. Do đó nó là một đồ thị liên thông.

Đồ thị ngắt kết nối

Một đồ thị G bị ngắt kết nối, nếu nó không chứa ít nhất hai đỉnh liên thông.

ví dụ 1

Đồ thị sau đây là một ví dụ về Đồ thị ngắt kết nối, trong đó có hai thành phần, một thành phần có các đỉnh 'a', 'b', 'c', 'd' và một thành phần khác với 'e', ​​'f', 'g', các đỉnh 'h'.

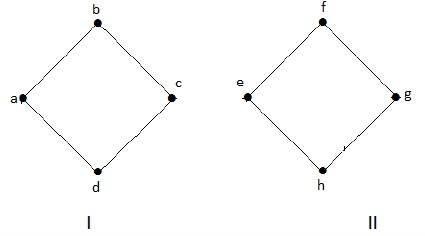
Hai thành phần độc lập và không kết nối với nhau. Do đó nó được gọi là đồ thị không kết nối.

Ví dụ 2

Trong ví dụ này, có hai thành phần độc lập, abfe và cd, không được kết nối với nhau. Do đó, đây là một đồ thị bị ngắt kết nối.

Biểu đồ thông thường

Một đồ thị G được cho là đều đặn, if all its vertices have the same degree. Trong một đồ thị, nếu tung độ của mỗi đỉnh là 'k' thì đồ thị đó được gọi là 'đồ thị k-đều'.

Thí dụ

Trong các đồ thị sau đây, tất cả các đỉnh có cùng tung độ. Vì vậy các đồ thị này được gọi là đồ thị chính quy.

Trong cả hai đồ thị, tất cả các đỉnh đều có bậc 2. Chúng được gọi là Đồ thị 2 chính quy.

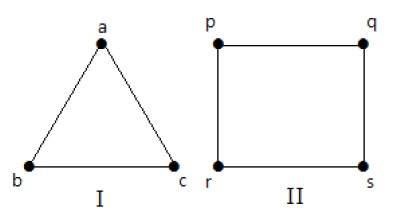
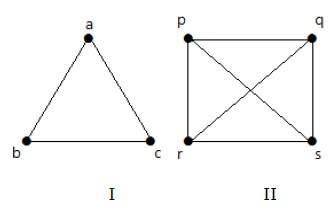
Đồ thị hoàn chỉnh

Một đồ thị đơn giản với 'n' đỉnh tương hỗ được gọi là đồ thị hoàn chỉnh và nó là denoted by ‘K_n’. Trong biểu đồ,a vertex should have edges with all other vertices, thì nó được gọi là một đồ thị hoàn chỉnh.

Nói cách khác, nếu một đỉnh được nối với tất cả các đỉnh khác trong một đồ thị, thì nó được gọi là một đồ thị hoàn chỉnh.

Thí dụ

Trong các đồ thị sau, mỗi đỉnh trong đồ thị được nối với tất cả các đỉnh còn lại trong đồ thị ngoại trừ chính nó.

Trong biểu đồ I,

	a	b	c
a	Không kết nối	Đã kết nối	Đã kết nối
b	Đã kết nối	Không kết nối	Đã kết nối
c	Đã kết nối	Đã kết nối	Không kết nối

Trong đồ thị II,

	p	q	r	S
p	Không kết nối	Đã kết nối	Đã kết nối	Đã kết nối
q	Đã kết nối	Không kết nối	Đã kết nối	Đã kết nối
r	Đã kết nối	Đã kết nối	Không kết nối	Đã kết nối
S	Đã kết nối	Đã kết nối	Đã kết nối	Không kết nối

Đồ thị chu kỳ

Một đồ thị đơn giản với 'n' đỉnh (n> = 3) và cạnh 'n' được gọi là đồ thị chu trình nếu tất cả các cạnh của nó tạo thành một chu trình có độ dài 'n'.

Nếu tung độ của mỗi đỉnh trong đồ thị là hai thì nó được gọi là Đồ thị chu kỳ.

Notation- C _n

Thí dụ

Hãy xem các biểu đồ sau:

• Đồ thị I có 3 đỉnh với 3 cạnh tạo thành một chu trình 'ab-bc-ca'.

• Đồ thị II có 4 đỉnh với 4 cạnh tạo thành một chu trình 'pq-qs-sr-rp'.

• Đồ thị III có 5 đỉnh với 5 cạnh tạo thành một chu trình 'ik-km-ml-lj-ji'.

Do đó tất cả các đồ thị đã cho đều là đồ thị chu trình.

Đồ thị bánh xe

Đồ thị bánh xe nhận được từ đồ thị chu trình C _n-1 bằng cách thêm một đỉnh mới. Đỉnh mới đó được gọi làHubđược nối với tất cả các đỉnh của C _n .

Kí hiệu - W _n

Số cạnh trong W _n = Số cạnh từ trung tâm đến tất cả các đỉnh khác +

Số cạnh từ tất cả các nút khác trong đồ thị chu trình mà không có trung tâm.

= (n – 1) + (n – 1)

= 2 (n – 1)

Thí dụ

Hãy xem các đồ thị sau đây. Chúng đều là đồ thị bánh xe.

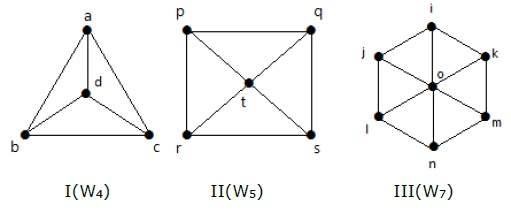
Trong đồ thị I, nó nhận được từ C ₃ bằng cách thêm một đỉnh ở giữa có tên là 'd'. Nó được ký hiệu là W ₄ .

Số cạnh trong W4 = 2 (n-1) = 2 (3) = 6

Trong đồ thị II, nó nhận được từ C4 bằng cách thêm một đỉnh ở giữa có tên là 't'. Nó được ký hiệu là W ₅ .

Số cạnh trong W5 = 2 (n-1) = 2 (4) = 8

Trong đồ thị III, nó nhận được từ C ₆ bằng cách thêm một đỉnh ở giữa có tên là 'o'. Nó được ký hiệu là W ₇ .

Số cạnh trong W4 = 2 (n-1) = 2 (6) = 12

Đồ thị tuần hoàn

Một đồ thị with at least one chu kỳ được gọi là đồ thị tuần hoàn.

Thí dụ

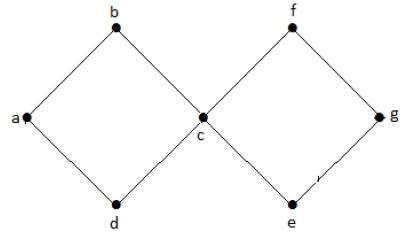
Trong đồ thị ví dụ trên, chúng ta có hai chu trình abcda và cfgec. Do đó nó được gọi là đồ thị tuần hoàn.

Đồ thị Acyclic

Một đồ thị with no cycles được gọi là đồ thị mạch hở.

Thí dụ

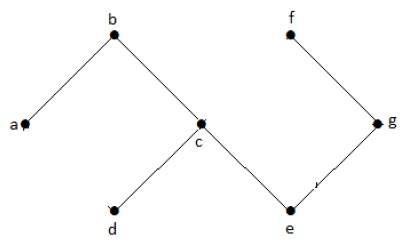
Trong đồ thị ví dụ trên, chúng ta không có bất kỳ chu trình nào. Do đó nó là một đồ thị không tuần hoàn.

Đồ thị hai bên

Một đồ thị đơn giản G = (V, E) với phân vùng đỉnh V = {V ₁ , V ₂ } được gọi là đồ thị lưỡng phânif every edge of E joins a vertex in V1 to a vertex in V₂.

Nói chung, một đồ thị Bipertite có hai tập đỉnh, giả sử, V1 và V2, và nếu một cạnh được vẽ, nó sẽ nối bất kỳ đỉnh nào trong tập V ₁ với bất kỳ đỉnh nào trong tập V ₂ .

Thí dụ

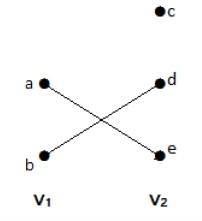
Trong đồ thị này, bạn có thể quan sát hai bộ đỉnh - V ₁ và V ₂ . Ở đây, hai cạnh có tên là 'ae' và 'bd' đang nối các đỉnh của hai tập V ₁ và V ₂ .

Đồ thị lưỡng cực hoàn chỉnh

Đồ thị hai góc 'G', G = (V, E) với phân hoạch V = {V ₁ , V ₂ } được cho là đồ thị lưỡng hợp hoàn chỉnh nếu mọi đỉnh trong V ₁ đều liên thông với mọi đỉnh của V ₂ .

Nói chung, một đồ thị lưỡng phân hoàn chỉnh nối mỗi đỉnh từ tập V ₁ với mỗi đỉnh từ tập V ₂ .

Thí dụ

Đồ thị sau đây là một đồ thị lưỡng hợp hoàn chỉnh vì nó có các cạnh nối mỗi đỉnh từ tập V ₁ với mỗi đỉnh từ tập V ₂ .

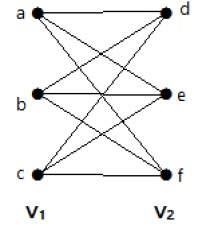
Nếu | V ₁ | = m và | V ₂ | = n, khi đó đồ thị lưỡng bội hoàn chỉnh được ký hiệu là K _{m, n} .

• K _{m, n} có (m + n) đỉnh và (mn) cạnh.
• K _{m, n} là đồ thị chính quy nếu m = n.

Nói chung, một complete bipartite graph is not a complete graph.

K _{m, n} là đồ thị đầy đủ nếu m = n = 1.

Số cạnh lớn nhất trong một đồ thị hai góc có n đỉnh là -

[n ^2/4 ]

Nếu n = 10, k5, 5 = [n2 / 4] = [10 ^2/4 ] = 25.

Tương tự, K6, 4 = 24

K7, 3 = 21

K8, 2 = 16

K9, 1 = 9

Nếu n = 9, k5, 4 = [n2 / 4] = [92/4] = 20

Tương tự, K6, 3 = 18

K7, 2 = 14

K8, 1 = 8

'G' là một đồ thị lưỡng phân nếu 'G' không có chu trình nào có độ dài lẻ. Một trường hợp đặc biệt của đồ thị lưỡng phân là đồ thị hình sao.

Đồ thị sao

Một đồ thị hai bên hoàn chỉnh có dạng K1, n-1 là một đồ thị hình sao với n đỉnh. Đồ thị hình sao là đồ thị lưỡng hợp hoàn chỉnh nếu một đỉnh đơn thuộc một tập hợp và tất cả các đỉnh còn lại thuộc tập hợp kia.

Thí dụ

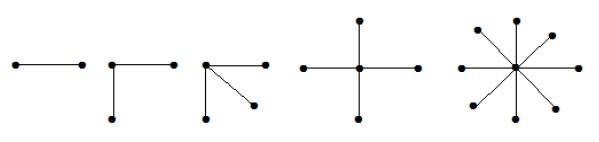
Trong các đồ thị trên, ngoài 'n' đỉnh, tất cả 'n-1' đều được nối với một đỉnh duy nhất. Do đó nó ở dạng K ¹ , ^n-1 là đồ thị hình sao.

Sự bổ sung của một đồ thị

Gọi 'G−' là một đồ thị đơn giản với một số đỉnh là của 'G' và một cạnh {U, V} nằm trong 'G−', nếu cạnh không có trong G. Điều đó có nghĩa là hai đỉnh kề nhau trong 'G−' nếu hai đỉnh không kề nhau trong G.

Nếu các cạnh tồn tại trong đồ thị I không có trong một đồ thị II khác và nếu cả đồ thị I và đồ thị II kết hợp với nhau để tạo thành một đồ thị hoàn chỉnh thì đồ thị I và đồ thị II được gọi là phần bù của nhau.

Thí dụ

Trong ví dụ sau, đồ thị-I có hai cạnh 'cd' và 'bd'. Đồ thị phần bù-II của nó có bốn cạnh.

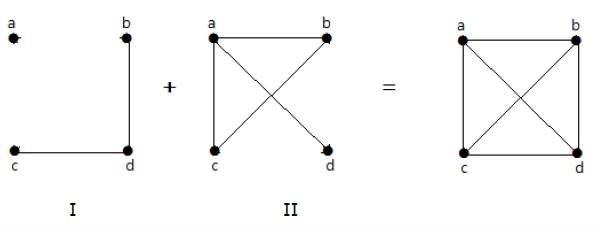
Lưu ý rằng các cạnh trong đồ thị-I không có trong đồ thị-II và ngược lại. Do đó, sự kết hợp của cả hai đồ thị sẽ cho một đồ thị hoàn chỉnh của 'n' đỉnh.

Note - Sự kết hợp của hai đồ thị bù nhau cho ta một đồ thị hoàn chỉnh.

Nếu 'G' là bất kỳ đồ thị đơn giản nào, thì

| E (G) | + | E ('G -') | = | E (Kn) |, trong đó n = số đỉnh trong đồ thị.

Thí dụ

Gọi 'G' là một đồ thị đơn giản có chín đỉnh và mười hai cạnh, tìm số cạnh trong 'G-'.

Bạn có, | E (G) | + | E ('G -') | = | E (Kn) |

12 + | E ('G -') | =

9 (9-1) / 2 = ⁹ C ₂

12 + | E ('G -') | = 36

| E ('G -') | = 24

'G' là một đồ thị đơn giản có 40 cạnh và phần bù của nó 'G−' có 38 cạnh. Tìm số đỉnh trong đồ thị G hoặc 'G−'.

Gọi số đỉnh trong đồ thị là 'n'.

Chúng ta có, | E (G) | + | E ('G -') | = | E (Kn) |

40 + 38 = n (n-1) / 2

156 = n (n-1)

13 (12) = n (n-1)

n = 13

Cây cối là đồ thị không chứa dù chỉ một chu trình. Chúng thể hiện cấu trúc phân cấp dưới dạng đồ họa. Cây cối thuộc loại đồ thị đơn giản nhất. Mặc dù đơn giản nhưng chúng có cấu trúc phong phú.

Cây cung cấp một loạt các ứng dụng hữu ích từ đơn giản như cây gia đình đến phức tạp như cây trong cấu trúc dữ liệu của khoa học máy tính.

Cây

A connected acyclic graphđược gọi là cây. Nói cách khác, một đồ thị liên thông không có chu trình được gọi là cây.

Các cạnh của cây được gọi là branches. Các phần tử của cây được gọi là nút của chúng. Các nút không có nút con được gọi làleaf nodes.

Cây có 'n' đỉnh có 'n-1' cạnh. Nếu nó có nhiều cạnh thừa hơn 'n-1', thì cạnh thừa rõ ràng phải ghép nối với hai đỉnh để tạo thành một chu trình. Sau đó, nó trở thành một đồ thị theo chu kỳ, điều này là vi phạm đối với đồ thị dạng cây.

Example 1

Biểu đồ được hiển thị ở đây là một cái cây vì nó không có chu trình và nó được kết nối với nhau. Nó có bốn đỉnh và ba cạnh, tức là đối với 'n' các cạnh 'n-1' như đã đề cập trong định nghĩa.

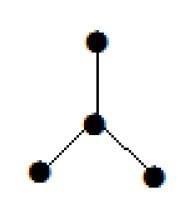
Note - Cây nào cũng có ít nhất hai đỉnh bậc một.

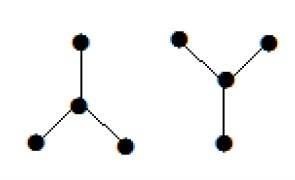
Example 2

Trong ví dụ trên, các đỉnh 'a' và 'd' có bậc một. Và hai đỉnh còn lại 'b' và 'c' có bậc hai. Điều này có thể xảy ra vì không tạo thành một chu trình, nên có ít nhất hai cạnh đơn ở bất kỳ đâu trong đồ thị. Nó không là gì ngoài hai cạnh với mức độ là một.

rừng

A disconnected acyclic graphđược gọi là rừng. Nói cách khác, một tập hợp cây rời rạc được gọi là rừng.

Example

Đồ thị sau đây giống như hai đồ thị con; nhưng nó là một đồ thị bị ngắt kết nối duy nhất. Không có chu trình nào trong đồ thị này. Do đó, rõ ràng nó là một khu rừng.

Cây kéo dài

Gọi G là một đồ thị liên thông, khi đó đồ thị con H của G được gọi là cây khung của G nếu -

• H là cây
• H chứa tất cả các đỉnh của G.

Cây bao trùm T của đồ thị vô hướng G là một đồ thị con bao gồm tất cả các đỉnh của G.

Example

Trong ví dụ trên, G là một đồ thị liên thông và H là một đồ thị con của G.

Rõ ràng, đồ thị H không có chu trình, nó là một cây có sáu cạnh nhỏ hơn tổng số đỉnh là một. Do đó H là cây Spanning của G.

Xếp hạng mạch

Gọi 'G' là một đồ thị liên thông với 'n' đỉnh và 'm' cạnh. Cây bao trùm 'T' của G chứa (n-1) cạnh.

Do đó, số cạnh bạn cần xóa khỏi 'G' để có được cây khung = m- (n-1), được gọi là bậc mạch của G.

Công thức này đúng, bởi vì trong cây khung, bạn cần có 'n-1' cạnh. Ngoài các cạnh 'm', bạn cần giữ lại các cạnh 'n – 1' trong biểu đồ.

Do đó, việc xóa các cạnh 'n – 1' khỏi 'm' sẽ cho các cạnh bị xóa khỏi biểu đồ để có được cây khung, cây không nên tạo thành một chu trình.

Example

Hãy xem biểu đồ sau:

Đối với đồ thị cho trong ví dụ trên, bạn có m = 7 cạnh và n = 5 đỉnh.

Khi đó hạng mạch là -

G = m - (n - 1)

= 7 - (5 - 1)

= 3

Example

Gọi 'G' là một đồ thị liên thông với sáu đỉnh và tung độ của mỗi đỉnh là ba. Tìm hạng mạch của 'G'.

Theo định lý tổng bậc của các đỉnh,

n Σ i=1deg (V _i ) = 2 | E |

6 × 3 = 2 | E |

| E | = 9

Hạng mạch = | E | - (| V | - 1)

= 9 - (6 - 1) = 4

Định lý Kirchoff

Định lý Kirchoff rất hữu ích trong việc tìm số cây khung có thể được hình thành từ một đồ thị liên thông.

Example

Ma trận 'A' được điền vào, nếu có một cạnh giữa hai đỉnh, thì nó sẽ được cho là '1', khác là '0'.

$$A=\begin{vmatrix}0 & a & b & c & d\\a & 0 & 1 & 1 & 1 \\b & 1 & 0 & 0 & 1\\c & 1 & 0 & 0 & 1\\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\\1 & 0 & 0 & 1\\1 & 0 & 0 & 1\\1 & 1 & 1 & 0\end{vmatrix}$$

Bằng cách sử dụng định lý kirchoff, nó sẽ được thay đổi như thay thế các giá trị đường chéo nguyên tắc bằng mức độ của các đỉnh và tất cả các phần tử khác bằng -1.A

$$=\begin{vmatrix} 3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$Co\:\:factor\:\:of\:\:m1\:\:= \begin{vmatrix} 2 & 0 & -1\\0 & 2 & -1\\-1 & -1 & 3\end{vmatrix}$$

Như vậy, số cây khung = 8.

Việc có thể đi ngang một đồ thị từ đỉnh này sang đỉnh khác hay không được xác định bởi cách một đồ thị được kết nối. Kết nối là một khái niệm cơ bản trong Lý thuyết đồ thị. Khả năng kết nối xác định xem một biểu đồ được kết nối hay bị ngắt kết nối. Nó có các chủ đề phụ dựa trên cạnh và đỉnh, được gọi là kết nối cạnh và kết nối đỉnh. Hãy để chúng tôi thảo luận chi tiết về chúng.

Kết nối

Một biểu đồ được cho là connected if there is a path between every pair of vertex. Từ mỗi đỉnh đến bất kỳ đỉnh nào khác, phải có một số đường đi qua. Đó được gọi là khả năng kết nối của một đồ thị. Một đồ thị có nhiều đỉnh và cạnh bị ngắt kết nối được cho là bị ngắt kết nối.

Example 1

Trong đồ thị sau, có thể đi từ đỉnh này sang bất kỳ đỉnh nào khác. Ví dụ, người ta có thể đi qua đỉnh 'a' đến đỉnh 'e' bằng cách sử dụng đường dẫn 'ab-e'.

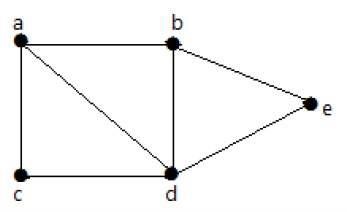
Example 2

Trong ví dụ sau, không thể đi qua đỉnh 'a' đến đỉnh 'f' vì không có đường đi giữa chúng trực tiếp hoặc gián tiếp. Do đó nó là một đồ thị bị ngắt kết nối.

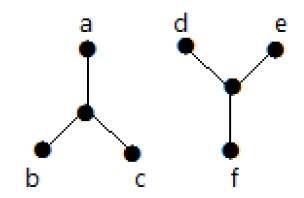
Cắt đỉnh

Gọi 'G' là một đồ thị liên thông. Một đỉnh V ∈ G được gọi là đỉnh cắt của 'G', nếu 'G-V' (Xóa 'V' khỏi 'G') dẫn đến một đồ thị bị ngắt kết nối. Việc xóa một đỉnh cắt khỏi biểu đồ sẽ chia nó thành hai hoặc nhiều đồ thị.

Note - Loại bỏ một đỉnh cắt có thể làm cho một đồ thị bị ngắt kết nối.

Một đồ thị liên thông 'G' có thể có nhiều nhất (n – 2) đỉnh cắt.

Example

Trong đồ thị sau, các đỉnh 'e' và 'c' là các đỉnh cắt.

Bằng cách loại bỏ 'e' hoặc 'c', đồ thị sẽ trở thành đồ thị bị ngắt kết nối.

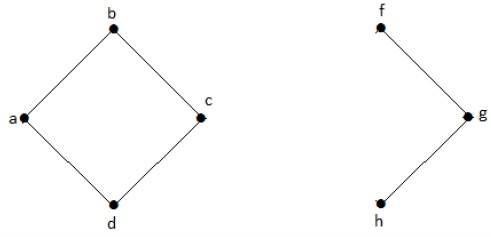
Không có 'g', không có đường đi giữa đỉnh 'c' và đỉnh 'h' và nhiều đường khác. Do đó, nó là một đồ thị không kết nối với đỉnh cắt là 'e'. Tương tự, 'c' cũng là một đỉnh cắt của đồ thị trên.

Cắt cạnh (Cầu)

Gọi 'G' là một đồ thị liên thông. Một cạnh 'e' ∈ G được gọi là một cạnh cắt nếu 'G-e' dẫn đến một đồ thị bị ngắt kết nối.

Nếu loại bỏ một cạnh trong biểu đồ dẫn đến hai hoặc nhiều đồ thị, thì cạnh đó được gọi là Cạnh cắt.

Example

Trong đồ thị sau, cạnh bị cắt là [(c, e)].

Bằng cách loại bỏ cạnh (c, e) khỏi đồ thị, nó sẽ trở thành một đồ thị bị ngắt kết nối.

Trong đồ thị trên, việc loại bỏ cạnh (c, e) sẽ chia đồ thị thành hai, không có gì khác ngoài đồ thị bị ngắt kết nối. Do đó, cạnh (c, e) là một cạnh cắt của đồ thị.

Note - Gọi 'G' là một đồ thị liên thông với 'n' đỉnh, khi đó

• một cạnh cắt e ∈ G nếu và chỉ khi cạnh 'e' không phải là một phần của bất kỳ chu trình nào trong G.

• số cạnh cắt tối đa có thể là 'n-1'.

• bất cứ khi nào các cạnh cắt tồn tại, các đỉnh bị cắt cũng tồn tại vì ít nhất một đỉnh của một cạnh cắt là một đỉnh cắt.

• nếu một đỉnh cắt tồn tại, thì một cạnh cắt có thể tồn tại hoặc không.

Cắt bộ đồ thị

Gọi 'G' = (V, E) là một đồ thị liên thông. Tập con E 'của E được gọi là tập cắt của G nếu việc xóa tất cả các cạnh của E' khỏi G làm cho G bị ngắt.

Nếu việc xóa một số cạnh nhất định khỏi đồ thị làm cho nó bị ngắt kết nối, thì những cạnh bị xóa đó được gọi là tập cắt của đồ thị.

Example

Hãy nhìn vào đồ thị sau đây. Tập hợp cắt của nó là E1 = {e1, e3, e5, e8}.

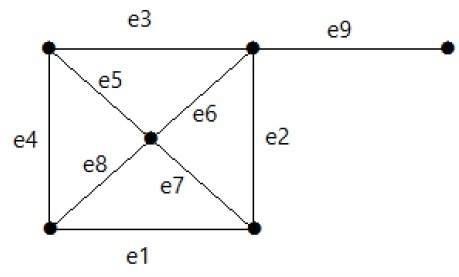
Sau khi loại bỏ tập cắt E1 khỏi đồ thị, nó sẽ xuất hiện như sau:

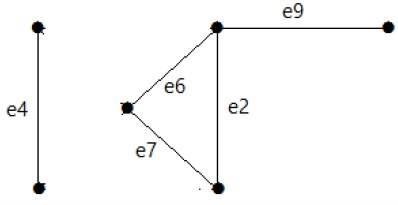
Tương tự, có những bộ cắt khác có thể ngắt kết nối đồ thị -

• E3 = {e9} - Tập hợp cắt nhỏ nhất của đồ thị.

• E4 = {e3, e4, e5}

Kết nối cạnh

Gọi 'G' là một đồ thị liên thông. Số cạnh tối thiểu mà việc loại bỏ làm cho 'G' bị ngắt kết nối được gọi là kết nối cạnh của G.

Notation - λ (G)

Nói cách khác, number of edges in a smallest cut set of G được gọi là kết nối cạnh của G.

Nếu 'G' có một cạnh cắt thì λ (G) là 1. (kết nối cạnh của G.)

Example

Hãy nhìn vào đồ thị sau đây. Bằng cách loại bỏ hai cạnh nhỏ nhất, đồ thị được kết nối sẽ bị ngắt kết nối. Do đó, kết nối cạnh của nó (λ (G)) là 2.

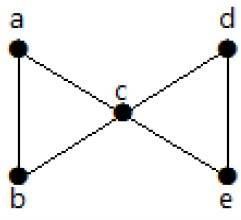
Dưới đây là bốn cách để ngắt kết nối biểu đồ bằng cách loại bỏ hai cạnh -

Kết nối đỉnh

Gọi 'G' là một đồ thị liên thông. Số lượng đỉnh tối thiểu mà việc loại bỏ làm cho 'G' bị ngắt kết nối hoặc giảm 'G' trong một đồ thị nhỏ được gọi là kết nối đỉnh của nó.

Notation - K (G)

Example

Trong đồ thị trên, việc loại bỏ các đỉnh 'e' và 'i' làm cho đồ thị bị ngắt kết nối.

Nếu G có đỉnh cắt thì K (G) = 1.

Notation - Đối với bất kỳ đồ thị liên thông G,

K (G) ≤ λ (G) ≤ δ (G)

Kết nối đỉnh (K (G)), kết nối cạnh (λ (G)), số độ tối thiểu của G (δ (G)).

Example

Tính λ (G) và K (G) cho đồ thị sau:

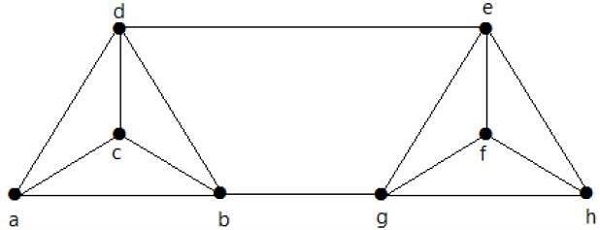
Solution

Từ biểu đồ,

δ (G) = 3

K (G) ≤ λ (G) ≤ δ (G) = 3 (1)

K (G) ≥ 2 (2)

Xóa các cạnh {d, e} và {b, h}, chúng ta có thể ngắt kết nối G.

Vì thế,

λ (G) = 2

2 ≤ λ (G) ≤ δ (G) = 2 (3)

Từ (2) và (3), kết nối đỉnh K (G) = 2

Đồ thị bao trùm là một đồ thị con chứa tất cả các đỉnh hoặc tất cả các cạnh tương ứng với một số đồ thị khác. Một đồ thị con chứa tất cả các đỉnh được gọi làline/edge covering. Một đồ thị con chứa tất cả các cạnh được gọi làvertex covering.

Bao phủ dòng

Cho G = (V, E) là một đồ thị. Một tập con C (E) được gọi là phủ dòng của G nếu mọi đỉnh của G là điểm trùng với ít nhất một cạnh trong C, tức là,

deg (V) ≥ 1 ∀ V ∈ G

vì mỗi đỉnh được nối với đỉnh khác bằng một cạnh. Do đó nó có mức độ tối thiểu là 1.

Example

Hãy xem biểu đồ sau:

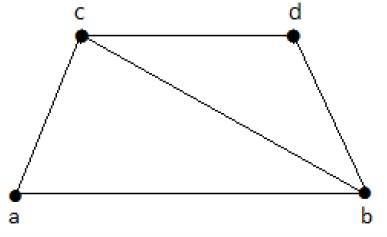
Các đồ thị con của nó có dòng bao phủ như sau:

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

Bao phủ dòng của 'G' không tồn tại nếu và chỉ khi 'G' có một đỉnh biệt lập. Đường bao của đồ thị có 'n' đỉnh có ít nhất [n / 2] cạnh.

Che phủ dòng tối thiểu

Một đường bao phủ C của đồ thị G được cho là cực tiểu if no edge can be deleted from C.

Example

Trong biểu đồ trên, các đồ thị con có dòng bao phủ như sau:

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

Ở đây, C ₁ , C ₂ , C ₃ là độ phủ dòng tối thiểu, còn C ₄ thì không vì chúng ta có thể xóa {b, c}.

Độ phủ dòng tối thiểu

Nó còn được gọi là Smallest Minimal Line Covering. Một đường bao phủ tối thiểu với số cạnh tối thiểu được gọi là phủ đường tối thiểu của 'G'. Số cạnh trong một dòng tối thiểu bao phủ trong 'G' được gọi làline covering numbercủa 'G' (α ₁ ).

Example

Trong ví dụ trên, C ₁ và C ₂ là đường bao nhỏ nhất của G và α ₁ = 2.

• Mỗi dòng phủ đều chứa một dòng tối thiểu.

• Mỗi phần phủ dòng không chứa phần phủ dòng tối thiểu (C ₃ không chứa phần phần dòng tối thiểu nào.

• Không có dòng tối thiểu bao gồm một chu kỳ.

• Nếu một dòng bao phủ 'C' không chứa đường dẫn có độ dài từ 3 trở lên, thì 'C' là một dòng tối thiểu bao phủ bởi vì tất cả các thành phần của 'C' đều là đồ thị hình sao và từ đồ thị hình sao, không có cạnh nào có thể bị xóa.

Che phủ đỉnh

Let ‘G’ = (V, E) be a graph. A subset K of V is called a vertex covering of ‘G’, if every edge of ‘G’ is incident with or covered by a vertex in ‘K’.

Example

Take a look at the following graph −

The subgraphs that can be derived from the above graph are as follows −

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

K₄ = {a, d}

Here, K₁, K₂, and K₃ have vertex covering, whereas K₄ does not have any vertex covering as it does not cover the edge {bc}.

Minimal Vertex Covering

A vertex ‘K’ of graph ‘G’ is said to be minimal vertex covering if no vertex can be deleted from ‘K’.

Example

In the above graph, the subgraphs having vertex covering are as follows −

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

Here, K₁ and K₂ are minimal vertex coverings, whereas in K₃, vertex ‘d’ can be deleted.

Minimum Vertex Covering

It is also known as the smallest minimal vertex covering. A minimal vertex covering of graph ‘G’ with minimum number of vertices is called the minimum vertex covering.

The number of vertices in a minimum vertex covering of ‘G’ is called the vertex covering number of G (α₂).

Example

In the following graph, the subgraphs having vertex covering are as follows −

K₁ = {b, c}

K₂ = {a, b, c}

K₃ = {b, c, d}

Here, K₁ is a minimum vertex cover of G, as it has only two vertices. α₂ = 2.

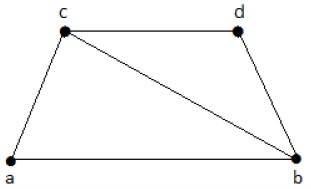
A matching graph is a subgraph of a graph where there are no edges adjacent to each other. Simply, there should not be any common vertex between any two edges.

Matching

Let ‘G’ = (V, E) be a graph. A subgraph is called a matching M(G), if each vertex of G is incident with at most one edge in M, i.e.,

deg(V) ≤ 1 ∀ V ∈ G

which means in the matching graph M(G), the vertices should have a degree of 1 or 0, where the edges should be incident from the graph G.

Notation − M(G)

Example

In a matching,

if deg(V) = 1, then (V) is said to be matched

if deg(V) = 0, then (V) is not matched.

In a matching, no two edges are adjacent. It is because if any two edges are adjacent, then the degree of the vertex which is joining those two edges will have a degree of 2 which violates the matching rule.

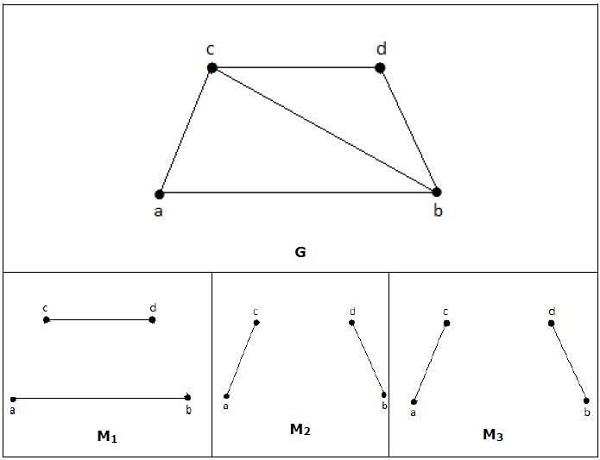
Maximal Matching

A matching M of graph ‘G’ is said to maximal if no other edges of ‘G’ can be added to M.

Example

M1, M2, M3 from the above graph are the maximal matching of G.

Maximum Matching

It is also known as largest maximal matching. Maximum matching is defined as the maximal matching with maximum number of edges.

The number of edges in the maximum matching of ‘G’ is called its matching number.

Example

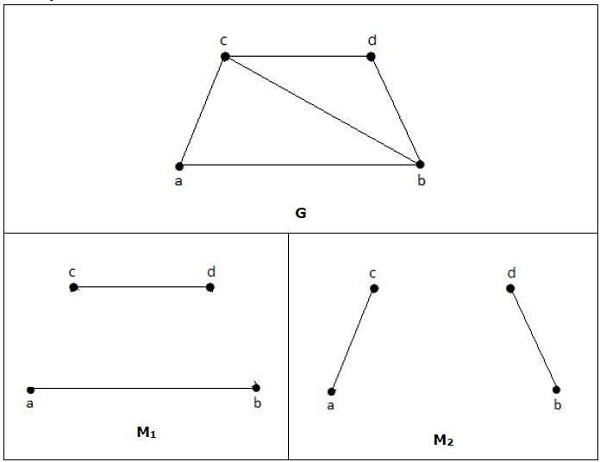
For a graph given in the above example, M1 and M2 are the maximum matching of ‘G’ and its matching number is 2. Hence by using the graph G, we can form only the subgraphs with only 2 edges maximum. Hence we have the matching number as two.

Perfect Matching

A matching (M) of graph (G) is said to be a perfect match, if every vertex of graph g (G) is incident to exactly one edge of the matching (M), i.e.,

deg(V) = 1 ∀ V

The degree of each and every vertex in the subgraph should have a degree of 1.

Example

In the following graphs, M1 and M2 are examples of perfect matching of G.

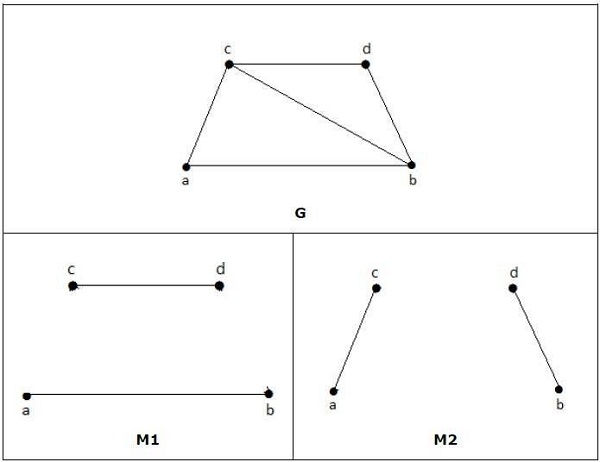
Note − Every perfect matching of graph is also a maximum matching of graph, because there is no chance of adding one more edge in a perfect matching graph.

A maximum matching of graph need not be perfect. If a graph ‘G’ has a perfect match, then the number of vertices |V(G)| is even. If it is odd, then the last vertex pairs with the other vertex, and finally there remains a single vertex which cannot be paired with any other vertex for which the degree is zero. It clearly violates the perfect matching principle.

Example

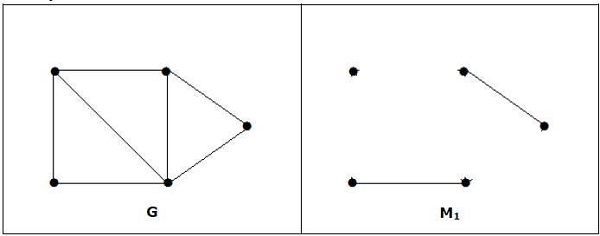
Note − The converse of the above statement need not be true. If G has even number of vertices, then M1 need not be perfect.

Example

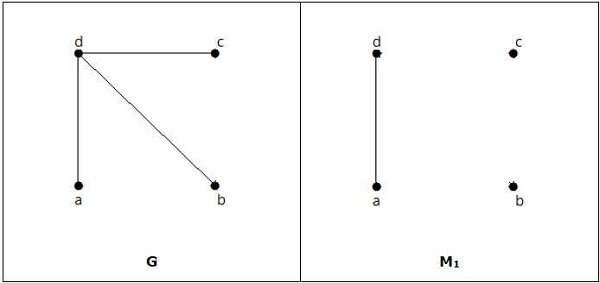
It is matching, but it is not a perfect match, even though it has even number of vertices.

Independent sets are represented in sets, in which

• there should not be any edges adjacent to each other. There should not be any common vertex between any two edges.

• there should not be any vertices adjacent to each other. There should not be any common edge between any two vertices.

Independent Line Set

Let ‘G’ = (V, E) be a graph. A subset L of E is called an independent line set of ‘G’ if no two edges in L are adjacent. Such a set is called an independent line set.

Example

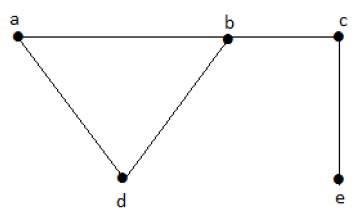
Let us consider the following subsets −

L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}

In this example, the subsets L2 and L3 are clearly not the adjacent edges in the given graph. They are independent line sets. However L1 is not an independent line set, as for making an independent line set, there should be at least two edges.

Maximal Independent Line Set

An independent line set is said to be the maximal independent line set of a graph ‘G’ if no other edge of ‘G’ can be added to ‘L’.

Example

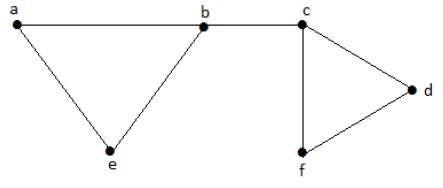
Let us consider the following subsets −

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L₂ and L₃ are maximal independent line sets/maximal matching. As for only these two subsets, there is no chance of adding any other edge which is not an adjacent. Hence these two subsets are considered as the maximal independent line sets.

Maximum Independent Line Set

A maximum independent line set of ‘G’ with maximum number of edges is called a maximum independent line set of ‘G’.

Number of edges in a maximum independent line set of G (β1)
   = Line independent number of G
   = Matching number of G

Example

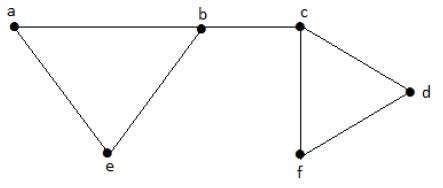
Let us consider the following subsets −

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L₃ is the maximum independent line set of G with maximum edges which are not the adjacent edges in graph and is denoted by β1 = 3.

Note − For any graph G with no isolated vertex,

α1 + β1 = number of vertices in a graph = |V|

Example

Line covering number of K_n/C_n/w_n,

$$\alpha 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:if\:n\:is\:even \\\frac{n+1}{2}\:if\:n\:is\:odd\end{cases}$$

Line independent number (Matching number) = β₁ = [n/2] α₁ + β₁ = n.

Independent Vertex Set

Let ‘G’ = (V, E) be a graph. A subset of ‘V’ is called an independent set of ‘G’ if no two vertices in ‘S’ are adjacent.

Example

Consider the following subsets from the above graphs −

S1 = {e}

S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Clearly S₁ is not an independent vertex set, because for getting an independent vertex set, there should be at least two vertices in the from a graph. But here it is not that case. The subsets S₂, S₃, and S₄ are the independent vertex sets because there is no vertex that is adjacent to any one vertex from the subsets.

Bộ đỉnh độc lập tối đa

Gọi 'G' là một đồ thị, khi đó tập đỉnh độc lập của 'G' được cho là cực đại nếu không có đỉnh nào khác của 'G' có thể được thêm vào 'S'.

Example

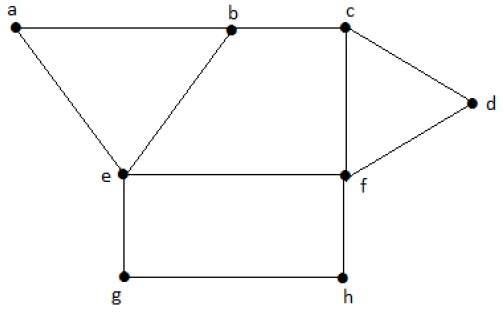
Hãy xem xét các tập hợp con sau từ các đồ thị trên.

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

S ₂ và S ₃ là các tập đỉnh độc lập cực đại của 'G'. Trong S ₁ và S ₄ , chúng ta có thể thêm các đỉnh khác; nhưng trong S ₂ và S ₃ , chúng ta không thể thêm bất kỳ đỉnh nào khác.

Bộ đỉnh độc lập tối đa

Tập đỉnh độc lập cực đại của 'G' với số đỉnh lớn nhất được gọi là tập đỉnh độc lập lớn nhất.

Example

Hãy xem xét các tập hợp con sau từ biểu đồ trên:

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Chỉ có S ₃ là tập đỉnh độc lập lớn nhất, vì nó bao gồm số lượng đỉnh cao nhất. Số đỉnh trong tập đỉnh độc lập tối đa của 'G' được gọi là số đỉnh độc lập của G (β ₂ ).

Example

Đối với đồ thị hoàn chỉnh K _n ,

Số phủ đỉnh = α ₂ = n − 1

Số độc lập đỉnh = β ₂ = 1

Bạn có α ₂ + β ₂ = n

Trong một đồ thị hoàn chỉnh, mỗi đỉnh kề với (n - 1) đỉnh còn lại của nó. Do đó, một tập K _n độc lập tối đa chỉ chứa một đỉnh.

Do đó, β ₂ = 1

và α ₂ = | v | - β ₂ = n-1

Note - Với bất kỳ đồ thị nào 'G' = (V, E)

• α ₂ + β ₂ = | v |
• Nếu 'S' là một tập đỉnh độc lập của 'G' thì (V - S) là một phủ đỉnh của G.

Tô màu đồ thị không có gì khác ngoài một cách đơn giản để gắn nhãn các thành phần đồ thị như đỉnh, cạnh và vùng theo một số ràng buộc. Trong một biểu đồ, không có hai đỉnh liền kề, các cạnh liền kề hoặc các vùng liền kề được tô màu với số lượng màu tối thiểu. Số này được gọi làchromatic number và đồ thị được gọi là properly colored graph.

Trong khi tô màu đồ thị, các ràng buộc được thiết lập trên đồ thị là màu sắc, thứ tự tô màu, cách gán màu, v.v. Màu được đưa ra cho một đỉnh hoặc một vùng cụ thể. Do đó, các đỉnh hoặc vùng có cùng màu tạo thành các tập hợp độc lập.

Màu Vertex

Tô màu đỉnh là phép gán màu cho các đỉnh của đồ thị 'G' sao cho không có hai đỉnh liền kề nào có cùng màu. Nói một cách đơn giản, không có hai đỉnh của một cạnh nào có cùng màu.

Số màu

Số màu tối thiểu cần thiết để tô màu đỉnh của đồ thị 'G' được gọi là số màu của G, ký hiệu là X (G).

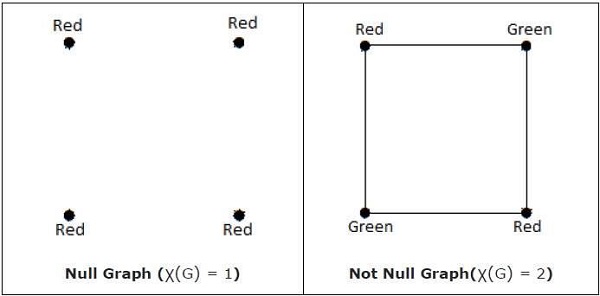
χ (G) = 1 nếu và chỉ khi 'G' là một đồ thị rỗng. Nếu 'G' không phải là đồ thị rỗng thì χ (G) ≥ 2.

Example

Note - Một đồ thị 'G' được cho là có thể xác định được n nếu có một màu đỉnh sử dụng nhiều nhất n màu, tức là X (G) ≤ n.

Màu vùng

Màu vùng là sự gán màu cho các vùng của biểu đồ phẳng sao cho không có hai vùng liền kề nào có cùng màu. Hai vùng được cho là liền kề nếu chúng có cạnh chung.

Example

Hãy nhìn vào đồ thị sau đây. Các vùng 'aeb' và 'befc' liền kề nhau, vì có một cạnh chung 'be' giữa hai vùng đó.

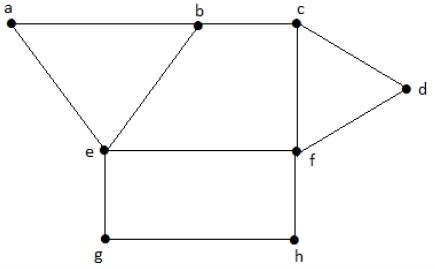
Tương tự, các vùng khác cũng được tô màu dựa trên vùng kề cận. Biểu đồ này được tô màu như sau:

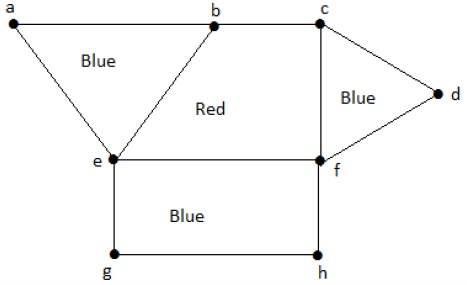
Example

Số sắc độ của Kn là

• n
• n–1
• [n/2]
• [n/2]

Hãy xem xét ví dụ này với K ₄ .

Trong đồ thị hoàn chỉnh, mỗi đỉnh kề với (n - 1) đỉnh còn lại. Do đó, mỗi đỉnh yêu cầu một màu mới. Do đó số màu của K _n = n.

Các ứng dụng của tô màu đồ thị

Tô màu đồ thị là một trong những khái niệm quan trọng nhất trong lý thuyết đồ thị. Nó được sử dụng trong nhiều ứng dụng thời gian thực của khoa học máy tính như -

• Clustering
• Khai thác dữ liệu
• Chụp ảnh
• Phân đoạn hình ảnh
• Networking
• Phân bổ nguồn lực
• Lập lịch xử lý

Một đồ thị có thể tồn tại ở các dạng khác nhau có cùng số đỉnh, số cạnh và cùng một kết nối cạnh. Đồ thị như vậy được gọi là đồ thị đẳng tích. Lưu ý rằng chúng tôi gắn nhãn các biểu đồ trong chương này chủ yếu nhằm mục đích tham khảo và nhận biết chúng với nhau.

Đồ thị đẳng hình

Hai đồ thị G ₁ và G ₂ được cho là đẳng tích nếu -

• Số thành phần của chúng (đỉnh và cạnh) là như nhau.

• Kết nối cạnh của họ vẫn được giữ lại.

Note- Tóm lại, trong số hai đồ thị đẳng tích, một đồ thị là phiên bản tinh chỉnh của đồ thị kia. Một đồ thị không có nhãn cũng có thể được coi là một đồ thị đẳng hình.

There exists a function ‘f’ from vertices of G1 to vertices of G2
   [f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.

Note

Nếu G ₁ ≡ G ₂ thì -

| V (G ₁ ) | = | V (G ₂ ) |

| E (G ₁ ) | = | E (G ₂ ) |

Trình tự bậc của G ₁ và G ₂ giống nhau.

Nếu các đỉnh {V ₁ , V ₂ , .. Vk} tạo thành một chu trình có độ dài K trong G ₁ , thì các đỉnh {f (V ₁ ), f (V ₂ ),… f (Vk)} sẽ tạo thành một chu trình có độ dài K trong G ₂ .

Tất cả các điều kiện trên là cần thiết để đồ thị G ₁ và G ₂ là đẳng tích, nhưng không đủ để chứng minh rằng đồ thị là đẳng tích.

• (G ₁ ≡ G ₂ ) nếu và chỉ khi (G ₁ - ≡ G ₂ -) trong đó G ₁ và G ₂ là các đồ thị đơn giản.

• (G ₁ ≡ G ₂ ) nếu ma trận kề của G ₁ và G ₂ giống nhau.

• (G ₁ ≡ G ₂ ) nếu và chỉ khi các đồ thị con tương ứng của G ₁ và G ₂ (thu được bằng cách xóa một số đỉnh trong G1 và ảnh của chúng trong đồ thị G ₂ ) là đẳng hình.

Example

Đồ thị nào sau đây là đồ thị đẳng tích?

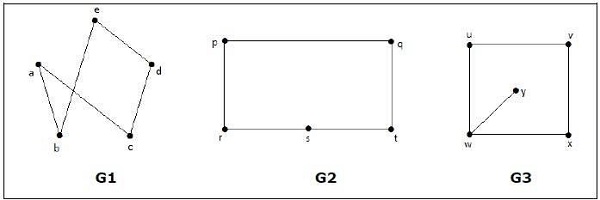
Trong đồ thị G ₃ , đỉnh 'w' chỉ có bậc 3, trong khi tất cả các đỉnh khác của đồ thị có bậc 2. Do đó G3 không đồng hình với G ₁ hoặc G ₂ .

Bổ sung G ₁ và G ₂ , bạn có -

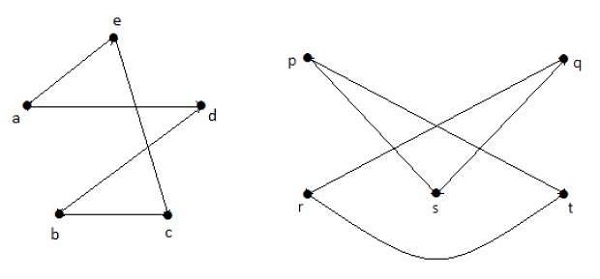
Ở đây, (G ₁ - ≡ G ₂ -), do đó (G ₁ ≡ G ₂ ).

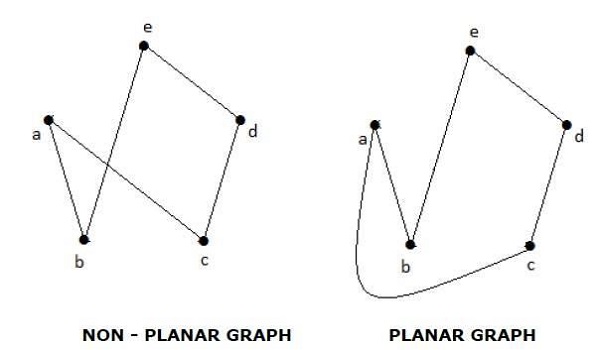
Đồ thị phẳng

Một đồ thị 'G' được cho là phẳng nếu nó có thể được vẽ trên một mặt phẳng hoặc một hình cầu sao cho không có hai cạnh nào cắt nhau tại một điểm không phải là đỉnh.

Example

Vùng

Mọi đồ thị phẳng đều chia mặt phẳng thành các vùng được kết nối với nhau được gọi là các vùng.

Example

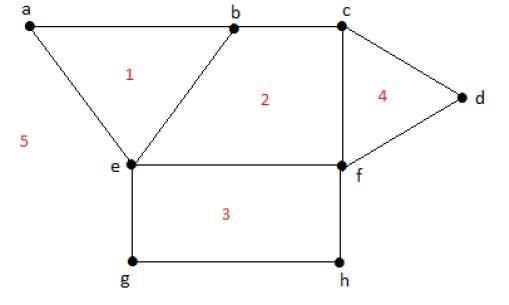
Mức độ của một vùng giới hạn r = deg(r) = Số cạnh bao quanh các vùng r.

deg(1) = 3
deg(2) = 4
deg(3) = 4

deg(4) = 3
deg(5) = 8

Mức độ của một vùng không giới hạn r = deg(r) = Số cạnh bao quanh các vùng r.

deg(R1) = 4
deg(R2) = 6

Trong đồ thị phẳng, các thuộc tính sau đây tốt:

Trong một đồ thị phẳng có 'n' đỉnh, tổng bậc của tất cả các đỉnh là:

n Σ i = 1 deg (V _i ) = 2 | E |

Dựa theo Sum of Degrees of Regions/ Định lý, trong một đồ thị phẳng có 'n' vùng, Tổng độ của các vùng là -

n Σ i = 1 deg (ri) = 2 | E |

Dựa vào định lý trên, bạn có thể rút ra các kết luận sau:

Trong một biểu đồ phẳng,

Nếu độ của mỗi vùng là K, thì tổng độ của các vùng là -

K | R | = 2 | E |

Nếu mức độ của mỗi vùng ít nhất là K (≥ K), thì

K | R | ≤ 2 | E |

Nếu mức độ của mỗi vùng tối đa là K (≤ K), thì

K | R | ≥ 2 | E |

Note - Giả sử rằng tất cả các khu vực có cùng mức độ.

Dựa theo Euler’s Formulae trên đồ thị phẳng,

Nếu đồ thị 'G' là một hình phẳng liên thông, thì

| V | + | R | = | E | + 2

Nếu một đồ thị phẳng với các thành phần 'K', thì

| V | + | R | = | E | + (K + 1)

Ở đâu, | V | là số đỉnh, | E | là số cạnh, và | R | là số vùng.

Bất bình đẳng cạnh đỉnh

Nếu 'G' là một đồ thị phẳng liên thông với mức độ của mỗi vùng ít nhất là 'K' thì,

| E | ≤ k / (k-2) {| v | - 2}

Bạn biết đấy, | V | + | R | = | E | + 2

K. | R | ≤ 2 | E |

K (| E | - | V | + 2) ≤ 2 | E |

(K - 2) | E | ≤ K (| V | - 2)

| E | ≤ k / (k-2) {| v | - 2}

Nếu 'G' là một đồ thị phẳng liên thông đơn giản, thì

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

Tồn tại ít nhất một đỉnh V • ∈ G sao cho deg (V) ≤ 5.

Nếu 'G' là một đồ thị phẳng liên thông đơn giản (có ít nhất 2 cạnh) và không có hình tam giác, thì

|E| ≤ {2|V| – 4}

Định lý Kuratowski

Một đồ thị 'G' là không phẳng nếu và chỉ khi 'G' có một đồ thị con là đồng phân hình với K ₅ hoặc K _3,3 .

Đồng tính

Hai đồ thị G ₁ và G ₂ được cho là đồng hình, nếu mỗi đồ thị này có thể nhận được từ cùng một đồ thị 'G' bằng cách chia một số cạnh của G có nhiều đỉnh hơn. Hãy xem ví dụ sau:

Chia cạnh 'rs' thành hai cạnh bằng cách thêm một đỉnh.

Các đồ thị dưới đây là đồng hình với đồ thị đầu tiên.

Nếu G ₁ là đồng phân với G ₂ , thì G là đồng phân với G2 nhưng điều ngược lại không cần phải đúng.

• Bất kỳ đồ thị nào có 4 đỉnh trở xuống đều là hình phẳng.

• Bất kỳ đồ thị nào có 8 cạnh trở xuống đều là hình phẳng.

• Một đồ thị hoàn chỉnh K _n là phẳng khi và chỉ khi n ≤ 4.

• Đồ thị lưỡng bội hoàn chỉnh K _{m, n} là đồng phẳng khi và chỉ khi m ≤ 2 hoặc n ≤ 2.

• Một đồ thị đơn giản không phẳng với số đỉnh tối thiểu là đồ thị hoàn chỉnh K ₅ .

• Đồ thị đơn giản không phẳng có số cạnh nhỏ nhất là K _{3; 3} .

Đồ thị đa diện

Một đồ thị phẳng liên thông đơn giản được gọi là đồ thị đa diện nếu tung độ của mỗi đỉnh là ≥ 3, tức là deg (V) ≥ 3 ∀ V ∈ G.

• 3 | V | ≤ 2 | E |

• 3 | R | ≤ 2 | E |

Một đồ thị có thể duyệt qua nếu bạn có thể vẽ một đường dẫn giữa tất cả các đỉnh mà không cần rút lại cùng một đường dẫn. Dựa trên đường dẫn này, có một số loại như đường dẫn của Euler và mạch của Euler được mô tả trong chương này.

Con đường của Euler

Đường đi của Euler chứa mỗi cạnh của 'G' đúng một lần và mỗi đỉnh của 'G' ít nhất một lần. Đồ thị liên thông G được cho là có thể duyệt qua nếu nó chứa đường đi của Euler.

Example

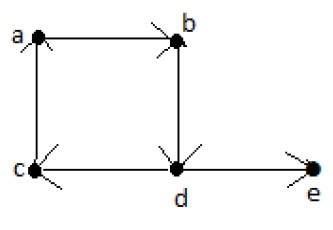
Đường dẫn của Euler = dcabde.

Mạch của Euler

Trong đường đi của Euler, nếu đỉnh bắt đầu giống với đỉnh kết thúc của nó, thì nó được gọi là mạch của Euler.

Example

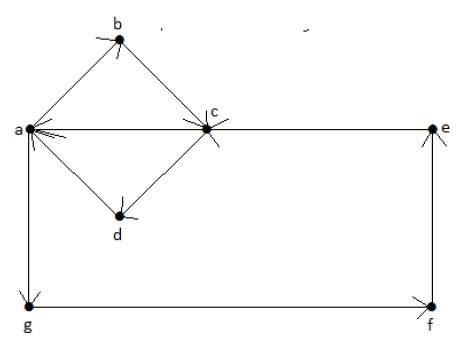
Euler’s Path = abcdagfeca.

Định lý mạch của Euler

Đồ thị liên thông 'G' có thể đi qua được nếu và chỉ khi số đỉnh có bậc lẻ trong G chính xác là 2 hoặc 0. Một đồ thị liên thông G có thể chứa đường đi của Euler, nhưng không phải là mạch của Euler, nếu nó có đúng hai đỉnh với một mức độ kỳ quặc.

Note - Đường đi Euler này bắt đầu với một đỉnh có bậc lẻ và kết thúc bằng một đỉnh khác có bậc lẻ.

Example

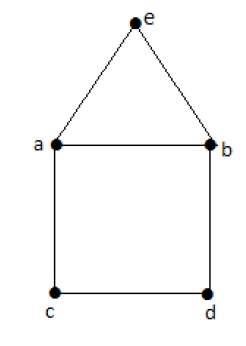
Euler’s Path- beabdca không phải là mạch của Euler, nhưng nó là đường dẫn của Euler. Rõ ràng nó có đúng 2 đỉnh bậc lẻ.

Note - Trong đồ thị liên thông G, nếu số đỉnh có bậc lẻ = 0 thì mạch Euler tồn tại.

Đồ thị Hamilton

Đồ thị liên thông G được cho là đồ thị Hamilton, nếu tồn tại một chu trình chứa tất cả các đỉnh của G.

Mỗi chu kỳ là một mạch nhưng một mạch có thể chứa nhiều chu kỳ. Một chu kỳ như vậy được gọi làHamiltonian cycle của G.

Đường đi Hamilton

Một đồ thị liên thông được cho là Hamilton nếu nó chứa mỗi đỉnh của G đúng một lần. Con đường như vậy được gọi làHamiltonian path.

Example

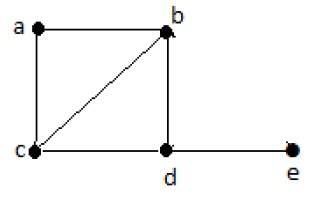
Hamiltonian Path- edbac.

Note

• Mạch của Euler chứa mỗi cạnh của đồ thị đúng một lần.

• Trong một chu trình Hamilton, một số cạnh của đồ thị có thể bị bỏ qua.

Example

Hãy xem biểu đồ sau:

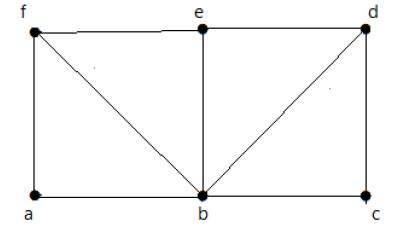
Đối với biểu đồ được hiển thị ở trên -

• Đường dẫn Euler tồn tại - sai

• Mạch Euler tồn tại - sai

• Chu trình Hamilton tồn tại - đúng

• Đường Hamilton tồn tại - đúng

G có bốn đỉnh có bậc lẻ nên không thể đi qua được. Bằng cách bỏ qua các cạnh bên trong, đồ thị có một chu trình Hamilton đi qua tất cả các đỉnh.

Trong chương này, chúng tôi sẽ trình bày một vài ví dụ tiêu chuẩn để chứng minh các khái niệm mà chúng tôi đã thảo luận trong các chương trước.

ví dụ 1

Find the number of spanning trees in the following graph.

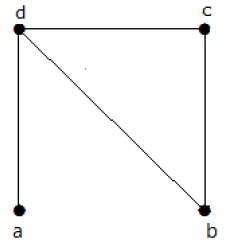
Giải pháp

Số cây khung thu được từ đồ thị trên là 3. Chúng như sau:

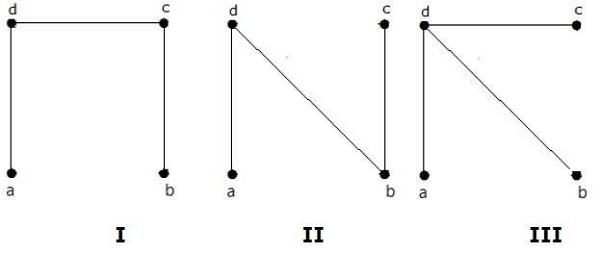
Ba cây này là cây bao trùm cho các đồ thị đã cho. Ở đây đồ thị I và II là đẳng tích của nhau. Rõ ràng, số cây khung không đẳng cấu là hai.

Ví dụ 2

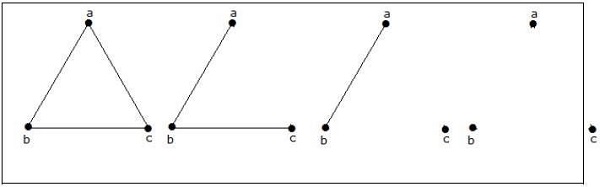
How many simple non-isomorphic graphs are possible with 3 vertices?

Giải pháp

Có thể có 4 đồ thị không đẳng phương có 3 đỉnh. Chúng được hiển thị bên dưới.

Ví dụ 3

Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.

Giải pháp

Theo định lý tổng độ,

20 Σ i = 1 deg (Vi) = 2 | E |

20 (3) = 2 | E |

| E | = 30

Theo công thức của Euler,

| V | + | R | = | E | + 2

20+ | R | = 30 + 2

| R | = 12

Do đó, số vùng là 12.

Ví dụ 4

What is the chromatic number of complete graph K_n?

Giải pháp

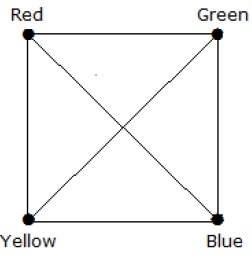
Trong một đồ thị hoàn chỉnh, mỗi đỉnh kề với còn lại (n – 1) đỉnh. Do đó, mỗi đỉnh yêu cầu một màu mới. Do đó số sắc K _n = n.

Ví dụ 5

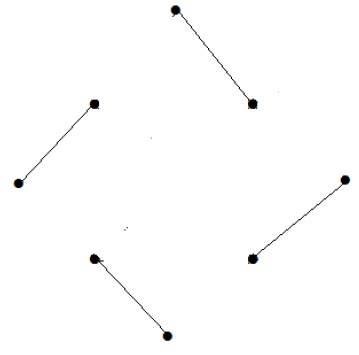
What is the matching number for the following graph?

Giải pháp

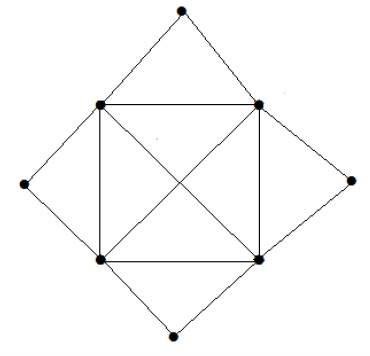
Số đỉnh = 9

Chúng ta chỉ có thể ghép 8 đỉnh.

Số phù hợp là 4.

Ví dụ 6

What is the line covering number of for the following graph?

Giải pháp

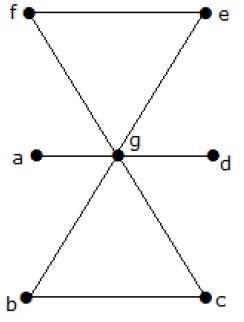
Số đỉnh = | V | = n = 7

Số phủ dòng = (α ₁ ) ≥ [n / 2] = 3

α ₁ ≥ 3

Bằng cách sử dụng 3 cạnh, chúng ta có thể bao gồm tất cả các đỉnh.

Do đó, số lượng dòng bao phủ là 3.