Lý thuyết đồ thị - Bộ độc lập
Các tập hợp độc lập được biểu diễn trong các tập hợp, trong đó
không nên có any edges adjacent to each other. Không nên có bất kỳ đỉnh chung nào giữa hai cạnh bất kỳ.
không nên có any vertices adjacent to each other. Không nên có bất kỳ cạnh chung nào giữa hai đỉnh bất kỳ.
Bộ dòng độc lập
Cho 'G' = (V, E) là một đồ thị. Tập con L của E được gọi là tập dòng độc lập của 'G' nếu không có hai cạnh nào trong L là kề nhau. Tập hợp như vậy được gọi là tập hợp dòng độc lập.
Example
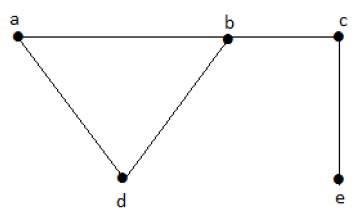
Chúng ta hãy xem xét các tập hợp con sau:
L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}Trong ví dụ này, các tập con L2 và L3 rõ ràng không phải là các cạnh liền kề trong đồ thị đã cho. Chúng là những tập hợp dòng độc lập. Tuy nhiên L1 không phải là một tập hợp dòng độc lập, vì để tạo một tập hợp dòng độc lập, cần có ít nhất hai cạnh.
Bộ dòng độc lập tối đa
Tập hợp đường độc lập được cho là tập hợp đường độc lập cực đại của đồ thị 'G' nếu không có cạnh nào khác của 'G' có thể được thêm vào 'L'.
Example
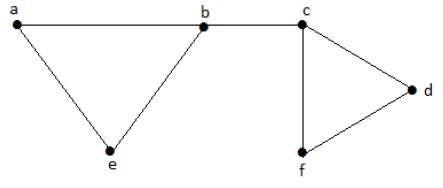
Chúng ta hãy xem xét các tập hợp con sau:
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L 2 và L 3 là các bộ dòng độc lập cực đại / đối sánh cực đại. Đối với chỉ hai tập hợp con này, không có cơ hội thêm bất kỳ cạnh nào khác không phải là liền kề. Do đó hai tập con này được coi là tập dòng độc lập cực đại.
Bộ dòng độc lập tối đa
Tập hợp dòng độc lập tối đa của 'G' với số cạnh tối đa được gọi là tập hợp dòng độc lập tối đa của 'G'.
Number of edges in a maximum independent line set of G (β1)
= Line independent number of G
= Matching number of GExample
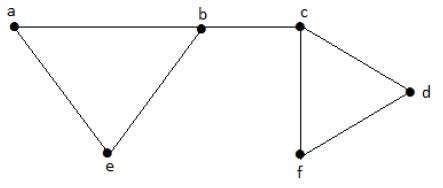
Chúng ta hãy xem xét các tập hợp con sau:
L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}L 3 là tập đường thẳng độc lập lớn nhất của G với các cạnh lớn nhất không phải là các cạnh liền kề trong đồ thị và được ký hiệu là β1 = 3.
Note - Đối với bất kỳ đồ thị G nào không có đỉnh biệt lập,
α1 + β1 = số đỉnh trong đồ thị = | V |
Example
Số dòng bao phủ K n / C n / w n ,
$$ \ alpha 1 = \ lceil \ frac {n} {2} \ rceil \ begin {case} \ frac {n} {2} \: if \: n \: is \: Even \\\ frac {n + 1} {2} \: if \: n \: là \: lẻ \ end {case} $$Số độc lập dòng (Số khớp) = β 1 = [n / 2] α 1 + β 1 = n.
Bộ đỉnh độc lập
Cho 'G' = (V, E) là một đồ thị. Tập hợp con của 'V' được gọi là tập độc lập của 'G' nếu không có hai đỉnh nào trong 'S' kề nhau.
Example

Hãy xem xét các tập hợp con sau từ các biểu đồ trên:
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}Rõ ràng S 1 không phải là một tập đỉnh độc lập, vì để có được một tập đỉnh độc lập, cần có ít nhất hai đỉnh trong từ đồ thị. Nhưng ở đây nó không phải là trường hợp đó. Các tập con S 2 , S 3 và S 4 là các tập đỉnh độc lập vì không có đỉnh nào kề với bất kỳ đỉnh nào từ các tập con.
Bộ đỉnh độc lập tối đa
Gọi 'G' là một đồ thị, khi đó tập đỉnh độc lập của 'G' được cho là cực đại nếu không có đỉnh nào khác của 'G' có thể được thêm vào 'S'.
Example
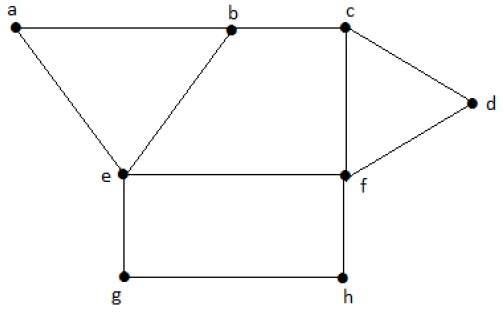
Hãy xem xét các tập hợp con sau từ các đồ thị trên.
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}S 2 và S 3 là các tập đỉnh độc lập cực đại của 'G'. Trong S 1 và S 4 , chúng ta có thể thêm các đỉnh khác; nhưng trong S 2 và S 3 , chúng ta không thể thêm bất kỳ đỉnh nào khác.
Bộ đỉnh độc lập tối đa
Tập đỉnh độc lập cực đại của 'G' với số đỉnh tối đa được gọi là tập đỉnh độc lập lớn nhất.
Example

Hãy xem xét các tập hợp con sau từ biểu đồ trên:
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}Chỉ có S 3 là tập đỉnh độc lập lớn nhất, vì nó bao gồm số lượng đỉnh cao nhất. Số đỉnh trong tập đỉnh độc lập tối đa của 'G' được gọi là số đỉnh độc lập của G (β 2 ).
Example
Đối với đồ thị hoàn chỉnh K n ,
Số phủ đỉnh = α 2 = n − 1
Số độc lập đỉnh = β 2 = 1
Bạn có α 2 + β 2 = n
Trong một đồ thị hoàn chỉnh, mỗi đỉnh kề với (n - 1) đỉnh còn lại của nó. Do đó, một tập K n độc lập tối đa chỉ chứa một đỉnh.
Do đó, β 2 = 1
và α 2 = | v | - β 2 = n-1
Note - Với bất kỳ đồ thị nào 'G' = (V, E)
- α 2 + β 2 = | v |
- Nếu 'S' là một tập đỉnh độc lập của 'G' thì (V - S) là một phủ đỉnh của G.