Lý thuyết đồ thị - Kết hợp
Đồ thị phù hợp là một đồ thị con của đồ thị trong đó không có cạnh nào kề nhau. Đơn giản, không nên có bất kỳ đỉnh chung nào giữa hai cạnh bất kỳ.
Phù hợp
Cho 'G' = (V, E) là một đồ thị. Một đồ thị con được gọi là M (G) phù hợp,if each vertex of G is incident with at most one edge in M, I E,
deg (V) ≤ 1 ∀ V ∈ G
có nghĩa là trong đồ thị khớp M (G), các đỉnh phải có bậc bằng 1 hoặc 0, nơi các cạnh phải là điểm trùng với đồ thị G.
Notation - M (G)
Example
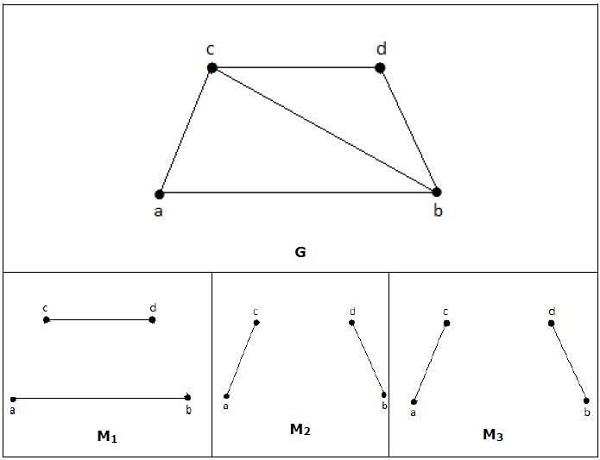

Trong một trận đấu,
nếu deg (V) = 1, thì (V) được cho là khớp
nếu deg (V) = 0, thì (V) không khớp.
Trong một kết hợp, không có hai cạnh nào liền nhau. Đó là bởi vì nếu bất kỳ hai cạnh nào kề nhau, thì bậc của đỉnh nối hai cạnh đó sẽ có bậc là 2, vi phạm quy tắc khớp.
Đối sánh tối đa
M phù hợp của đồ thị 'G' được cho là cực đại if no other edges of ‘G’ can be added to M.
Example

M1, M2, M3 từ đồ thị trên là những trùng khớp cực đại của G.
Phù hợp tối đa
Nó còn được gọi là so khớp cực đại lớn nhất. Đối sánh tối đa được định nghĩa là đối sánh tối đa với số cạnh tối đa.
Số cạnh trong kết hợp tối đa của 'G' được gọi là matching number.
Example
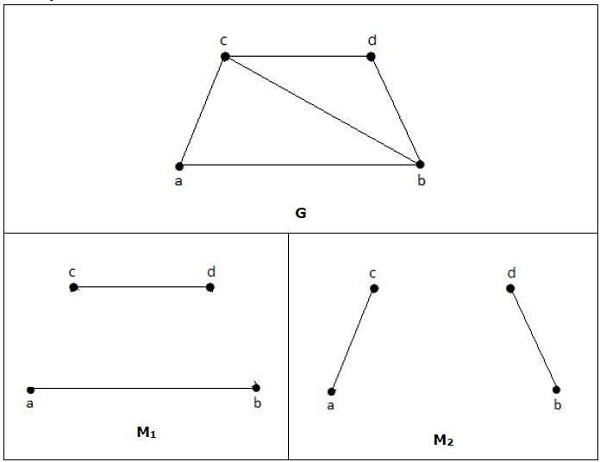
Đối với một đồ thị cho trong ví dụ trên, M1 và M2 là kết hợp tối đa của 'G' và số phù hợp của nó là 2. Do đó, bằng cách sử dụng đồ thị G, chúng ta chỉ có thể tạo ra các đồ thị con chỉ có 2 cạnh tối đa. Do đó, chúng tôi có số phù hợp là hai.
Kết hợp hoàn hảo
Một phép so khớp (M) của đồ thị (G) được cho là một sự kết hợp hoàn hảo, nếu mọi đỉnh của đồ thị g (G) là trùng với đúng một cạnh của phép so khớp (M), tức là
deg (V) = 1 ∀ V
Bậc của mỗi và mọi đỉnh trong đồ thị con phải có bậc bằng 1.
Example
Trong các đồ thị sau, M1 và M2 là các ví dụ về sự kết hợp hoàn hảo của G.
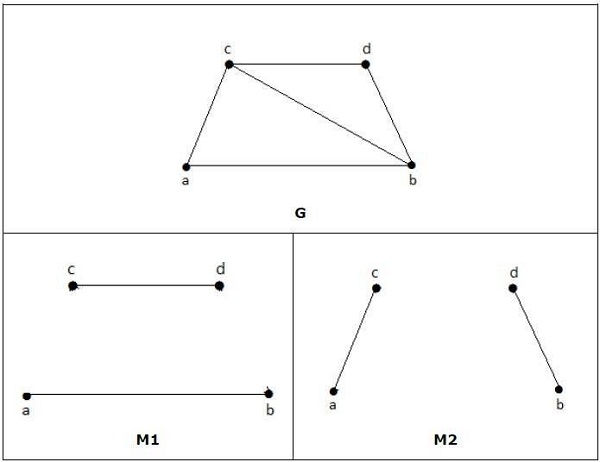
Note - Mọi kết hợp hoàn hảo của đồ thị cũng là một kết hợp tối đa của đồ thị, vì không có cơ hội thêm một cạnh nào nữa trong một đồ thị phù hợp hoàn hảo.
Một kết hợp tối đa của đồ thị không cần phải hoàn hảo. Nếu một đồ thị 'G' có một khớp hoàn hảo thì số đỉnh | V (G) | là thậm chí. Nếu nó là số lẻ, thì đỉnh cuối cùng sẽ ghép đôi với đỉnh còn lại, và cuối cùng vẫn còn lại một đỉnh duy nhất mà không thể ghép nối với bất kỳ đỉnh nào khác có tung độ bằng không. Nó rõ ràng vi phạm nguyên tắc kết hợp hoàn hảo.
Example
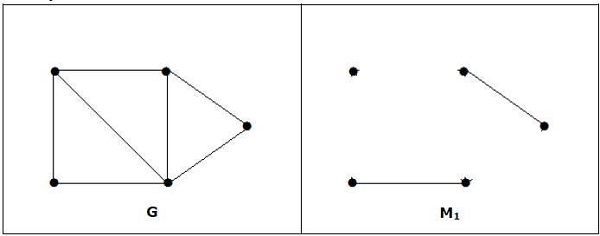
Note- Ý nghĩa của câu trên không nhất thiết phải đúng. Nếu G có số đỉnh chẵn thì M1 không cần hoàn hảo.
Example
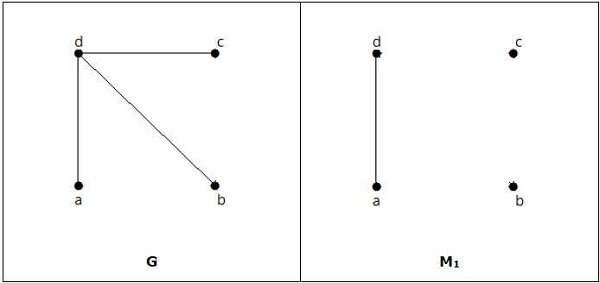
Nó phù hợp, nhưng nó không phải là một kết hợp hoàn hảo, mặc dù nó có số đỉnh chẵn.