Lý thuyết đồ thị - Khả năng truyền qua
Một đồ thị có thể duyệt qua nếu bạn có thể vẽ một đường dẫn giữa tất cả các đỉnh mà không cần rút lại cùng một đường dẫn. Dựa trên đường dẫn này, có một số loại như đường dẫn của Euler và mạch của Euler được mô tả trong chương này.
Con đường của Euler
Đường đi của Euler chứa mỗi cạnh của 'G' đúng một lần và mỗi đỉnh của 'G' ít nhất một lần. Đồ thị liên thông G được cho là có thể duyệt qua nếu nó chứa đường đi của Euler.
Example
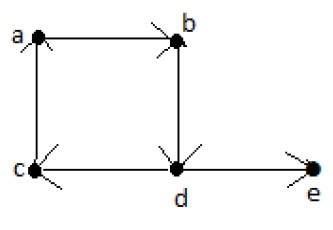
Đường dẫn của Euler = dcabde.
Mạch của Euler
Trong đường đi của Euler, nếu đỉnh bắt đầu giống với đỉnh kết thúc của nó, thì nó được gọi là mạch Euler.
Example
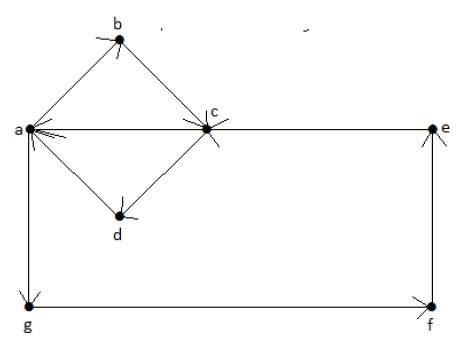
Euler’s Path = abcdagfeca.
Định lý mạch của Euler
Đồ thị liên thông 'G' có thể đi qua được nếu và chỉ khi số đỉnh có bậc lẻ trong G chính xác là 2 hoặc 0. Một đồ thị liên thông G có thể chứa đường đi của Euler, nhưng không phải là mạch của Euler, nếu nó có đúng hai đỉnh với một mức độ kỳ quặc.
Note - Đường đi Euler này bắt đầu với một đỉnh có bậc lẻ và kết thúc bằng một đỉnh khác có bậc lẻ.
Example
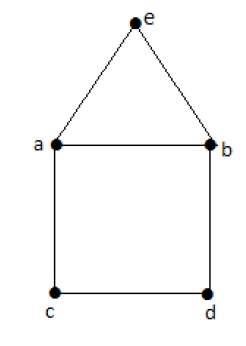
Euler’s Path- beabdca không phải là mạch của Euler, nhưng nó là đường dẫn của Euler. Rõ ràng nó có đúng 2 đỉnh bậc lẻ.
Note - Trong đồ thị liên thông G, nếu số đỉnh có bậc lẻ = 0 thì mạch Euler tồn tại.
Đồ thị Hamilton
Đồ thị liên thông G được cho là đồ thị Hamilton, nếu tồn tại một chu trình chứa tất cả các đỉnh của G.
Mỗi chu kỳ là một mạch nhưng một mạch có thể chứa nhiều chu kỳ. Một chu kỳ như vậy được gọi làHamiltonian cycle của G.
Đường đi Hamilton
Một đồ thị liên thông được cho là Hamilton nếu nó chứa mỗi đỉnh của G đúng một lần. Con đường như vậy được gọi làHamiltonian path.
Example
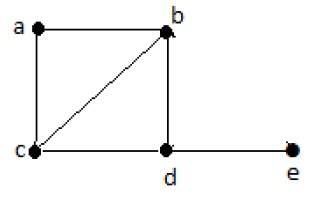
Hamiltonian Path- edbac.
Note
Mạch của Euler chứa mỗi cạnh của đồ thị đúng một lần.
Trong một chu trình Hamilton, một số cạnh của đồ thị có thể bị bỏ qua.
Example
Hãy xem biểu đồ sau:
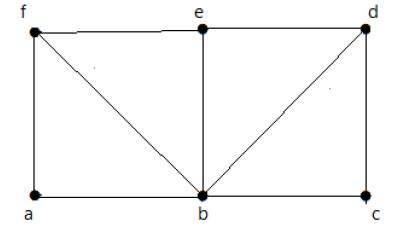
Đối với biểu đồ được hiển thị ở trên -
Đường dẫn Euler tồn tại - sai
Mạch Euler tồn tại - sai
Chu trình Hamilton tồn tại - đúng
Đường Hamilton tồn tại - đúng
G có bốn đỉnh có bậc lẻ nên không thể đi qua được. Bằng cách bỏ qua các cạnh bên trong, đồ thị có một chu trình Hamilton đi qua tất cả các đỉnh.