Lý thuyết đồ thị - Các loại đồ thị

Có nhiều loại đồ thị khác nhau tùy thuộc vào số lượng đỉnh, số cạnh, liên kết và cấu trúc tổng thể của chúng. Chúng ta sẽ chỉ thảo luận một số dạng đồ thị quan trọng nhất định trong chương này.

Đồ thị rỗng

A graph having no edges được gọi là Đồ thị rỗng.

Thí dụ

Trong đồ thị trên, có ba đỉnh được đặt tên là 'a', 'b' và 'c', nhưng không có cạnh nào trong số chúng. Do đó nó là Đồ thị rỗng.

Đồ thị tầm thường

A graph with only one vertex được gọi là Đồ thị tầm thường.

Thí dụ

Trong đồ thị trên, chỉ có một đỉnh 'a' không có cạnh nào khác. Do đó, nó là một đồ thị tầm thường.

Đồ thị không hướng

Một đồ thị không có hướng chứa các cạnh nhưng các cạnh không có hướng.

Thí dụ

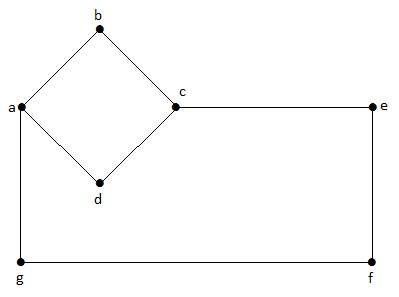
Trong biểu đồ này, 'a', 'b', 'c', 'd', 'e', 'f', 'g' là các đỉnh và 'ab', 'bc', 'cd', 'da ',' ag ',' gf ',' ef 'là các cạnh của đồ thị. Vì nó là một đồ thị không có hướng nên các cạnh 'ab' và 'ba' giống nhau. Tương tự các cạnh khác cũng xét theo cách tương tự.

Đồ thị hướng

Trong một đồ thị có hướng, mỗi cạnh có một hướng.

Thí dụ

Trong đồ thị trên, chúng ta có bảy đỉnh 'a', 'b', 'c', 'd', 'e', 'f' và 'g', và tám cạnh 'ab', 'cb', ' dc ',' ad ',' ec ',' fe ',' gf 'và' ga '. Vì nó là một đồ thị có hướng, mỗi cạnh có một dấu mũi tên cho biết hướng của nó. Lưu ý rằng trong đồ thị có hướng, 'ab' khác với 'ba'.

Đồ thị đơn giản

Một đồ thị with no loops và không parallel edges được gọi là một đồ thị đơn giản.

Số cạnh lớn nhất có thể có trong một đồ thị có 'n' đỉnh là ⁿ C ₂ trong đó ⁿ C ₂ = n (n - 1) / 2.
Số lượng đồ thị đơn giản có thể có 'n' đỉnh = 2 _{ⁿ c ₂} = 2 ^{n (n-1) / 2} .

Thí dụ

Trong đồ thị sau có 3 đỉnh có 3 cạnh là cực đại không kể cạnh và đường tròn song song. Điều này có thể được chứng minh bằng cách sử dụng các công thức trên.

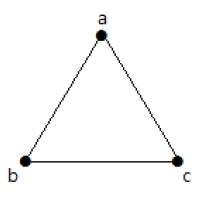
Số cạnh lớn nhất có n = 3 đỉnh -

ⁿ C ₂ = n (n – 1) / 2

= 3 (3–1) / 2

= 6/2

= 3 cạnh

Số lượng đồ thị đơn giản tối đa có n = 3 đỉnh -

2 _{ⁿ C ₂} = 2 ^{n (n-1) / 2}

= 2 ^{3 (3-1) / 2}

= 2 ³

số 8

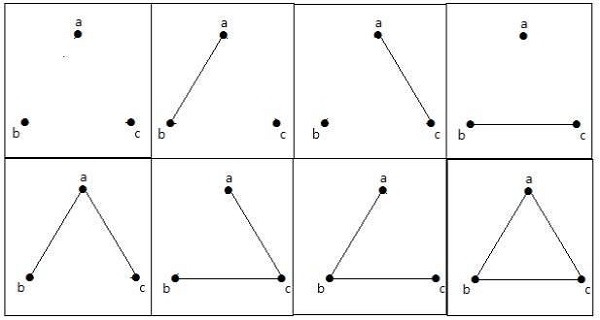
8 đồ thị này như hình dưới đây -

Biểu đồ được kết nối

Một đồ thị G được cho là liên kết if there exists a path between every pair of vertices. Nên có ít nhất một cạnh cho mọi đỉnh trong đồ thị. Vì vậy, chúng ta có thể nói rằng nó được kết nối với một số đỉnh khác ở phía bên kia của cạnh.

Thí dụ

Trong đồ thị sau, mỗi đỉnh có cạnh riêng của nó nối với cạnh khác. Do đó nó là một đồ thị liên thông.

Đồ thị ngắt kết nối

Một đồ thị G bị ngắt kết nối, nếu nó không chứa ít nhất hai đỉnh liên thông.

ví dụ 1

Biểu đồ sau là một ví dụ về Đồ thị ngắt kết nối, trong đó có hai thành phần, một thành phần có các đỉnh 'a', 'b', 'c', 'd' và một thành phần khác có các đỉnh 'e', 'f', 'g', các đỉnh 'h'.

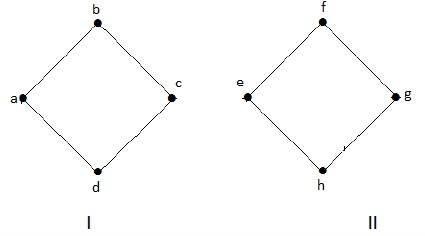
Hai thành phần độc lập và không kết nối với nhau. Do đó nó được gọi là đồ thị không kết nối.

Ví dụ 2

Trong ví dụ này, có hai thành phần độc lập, abfe và cd, không được kết nối với nhau. Do đó, đây là một đồ thị bị ngắt kết nối.

Biểu đồ thông thường

Một đồ thị G được cho là đều đặn, if all its vertices have the same degree. Trong một đồ thị, nếu tung độ của mỗi đỉnh là 'k', thì đồ thị đó được gọi là 'đồ thị k-đều'.

Thí dụ

Trong các đồ thị sau đây, tất cả các đỉnh có cùng tung độ. Vì vậy các đồ thị này được gọi là đồ thị chính quy.

Trong cả hai đồ thị, tất cả các đỉnh đều có bậc 2. Chúng được gọi là Đồ thị 2 chính quy.

Đồ thị hoàn chỉnh

Một đồ thị đơn giản với 'n' đỉnh tương hỗ được gọi là đồ thị hoàn chỉnh và nó là denoted by ‘K_n’. Trong biểu đồ,a vertex should have edges with all other vertices, thì nó được gọi là một đồ thị hoàn chỉnh.

Nói cách khác, nếu một đỉnh được nối với tất cả các đỉnh khác trong một đồ thị, thì nó được gọi là một đồ thị hoàn chỉnh.

Thí dụ

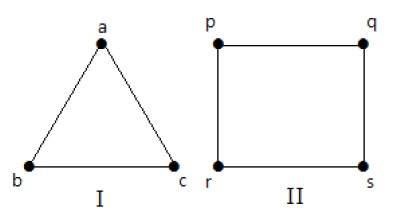
Trong các đồ thị sau, mỗi đỉnh trong đồ thị được nối với tất cả các đỉnh còn lại trong đồ thị ngoại trừ chính nó.

Trong biểu đồ I,

	a	b	c
a	Không kết nối	Đã kết nối	Đã kết nối
b	Đã kết nối	Không kết nối	Đã kết nối
c	Đã kết nối	Đã kết nối	Không kết nối

Trong đồ thị II,

	p	q	r	S
p	Không kết nối	Đã kết nối	Đã kết nối	Đã kết nối
q	Đã kết nối	Không kết nối	Đã kết nối	Đã kết nối
r	Đã kết nối	Đã kết nối	Không kết nối	Đã kết nối
S	Đã kết nối	Đã kết nối	Đã kết nối	Không kết nối

Đồ thị chu kỳ

Một đồ thị đơn giản với 'n' đỉnh (n> = 3) và cạnh 'n' được gọi là đồ thị chu trình nếu tất cả các cạnh của nó tạo thành một chu trình có độ dài 'n'.

Nếu tung độ của mỗi đỉnh trong đồ thị là hai, thì nó được gọi là Đồ thị chu kỳ.

Notation- C _n

Thí dụ

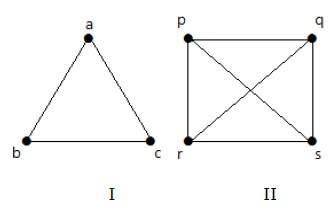
Hãy xem các biểu đồ sau:

Đồ thị I có 3 đỉnh với 3 cạnh tạo thành một chu trình 'ab-bc-ca'.
Đồ thị II có 4 đỉnh với 4 cạnh tạo thành một chu trình 'pq-qs-sr-rp'.
Đồ thị III có 5 đỉnh với 5 cạnh tạo thành một chu trình 'ik-km-ml-lj-ji'.

Do đó tất cả các đồ thị đã cho đều là đồ thị chu trình.

Đồ thị bánh xe

Đồ thị bánh xe thu được từ đồ thị chu trình C _n-1 bằng cách thêm một đỉnh mới. Đỉnh mới đó được gọi làHubđược nối với tất cả các đỉnh của C _n .

Kí hiệu - W _n

Số cạnh trong W _n = Số cạnh từ trung tâm đến tất cả các đỉnh khác +

Số cạnh từ tất cả các nút khác trong đồ thị chu trình mà không có trung tâm.

= (n – 1) + (n – 1)

= 2 (n – 1)

Thí dụ

Hãy xem các đồ thị sau đây. Chúng đều là đồ thị bánh xe.

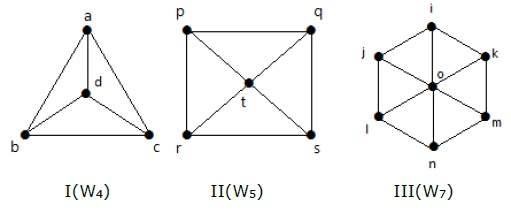
Trong đồ thị I, nó nhận được từ C ₃ bằng cách thêm một đỉnh ở giữa có tên là 'd'. Nó được ký hiệu là W ₄ .

Số cạnh trong W4 = 2 (n-1) = 2 (3) = 6

Trong đồ thị II, nó nhận được từ C4 bằng cách thêm một đỉnh ở giữa có tên là 't'. Nó được ký hiệu là W ₅ .

Số cạnh trong W5 = 2 (n-1) = 2 (4) = 8

Trong đồ thị III, nó nhận được từ C ₆ bằng cách thêm một đỉnh ở giữa có tên là 'o'. Nó được ký hiệu là W ₇ .

Số cạnh trong W4 = 2 (n-1) = 2 (6) = 12

Đồ thị tuần hoàn

Một đồ thị with at least one chu kỳ được gọi là đồ thị tuần hoàn.

Thí dụ

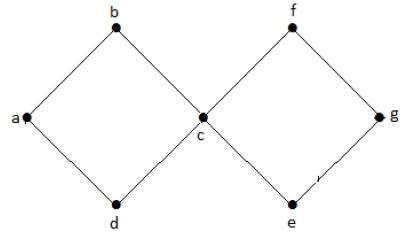
Trong đồ thị ví dụ trên, chúng ta có hai chu trình abcda và cfgec. Do đó nó được gọi là đồ thị tuần hoàn.

Đồ thị Acyclic

Một đồ thị with no cycles được gọi là đồ thị mạch hở.

Thí dụ

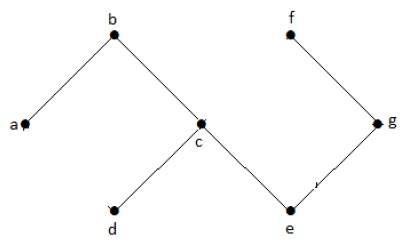
Trong đồ thị ví dụ trên, chúng ta không có bất kỳ chu trình nào. Do đó nó là một đồ thị không tuần hoàn.

Đồ thị hai bên

Một đồ thị đơn giản G = (V, E) với phân vùng đỉnh V = {V ₁ , V ₂ } được gọi là đồ thị lưỡng phânif every edge of E joins a vertex in V1 to a vertex in V₂.

Nói chung, một đồ thị Bipertite có hai tập đỉnh, giả sử là V1 và V2, và nếu một cạnh được vẽ, nó sẽ nối bất kỳ đỉnh nào trong tập V ₁ với bất kỳ đỉnh nào trong tập V ₂ .

Thí dụ

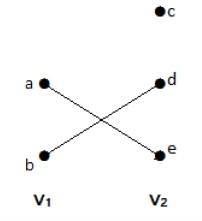
Trong đồ thị này, bạn có thể quan sát hai bộ đỉnh - V ₁ và V ₂ . Ở đây, hai cạnh có tên là 'ae' và 'bd' đang nối các đỉnh của hai tập V ₁ và V ₂ .

Đồ thị lưỡng cực hoàn chỉnh

Một đồ thị lưỡng phân 'G', G = (V, E) với phân hoạch V = {V ₁ , V ₂ } được cho là một đồ thị lưỡng phân hoàn chỉnh nếu mọi đỉnh trong V ₁ đều liên thông với mọi đỉnh của V ₂ .

Nói chung, một đồ thị lưỡng phân hoàn chỉnh nối mỗi đỉnh từ tập V ₁ với mỗi đỉnh từ tập V ₂ .

Thí dụ

Đồ thị dưới đây là một đồ thị lưỡng hợp hoàn chỉnh vì nó có các cạnh nối mỗi đỉnh từ tập V ₁ với mỗi đỉnh từ tập V ₂ .

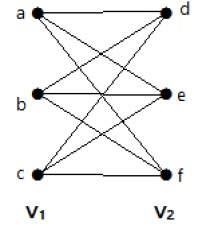
Nếu | V ₁ | = m và | V ₂ | = n, khi đó đồ thị lưỡng bội hoàn chỉnh được ký hiệu là K _{m, n} .

K _{m, n} có (m + n) đỉnh và (mn) cạnh.
K _{m, n} là đồ thị chính quy nếu m = n.

Nói chung, một complete bipartite graph is not a complete graph.

K _{m, n} là đồ thị đầy đủ nếu m = n = 1.

Số cạnh lớn nhất trong một đồ thị hai đỉnh có n đỉnh là -

[n ^2/4 ]

Nếu n = 10, k5, 5 = [n2 / 4] = [10 ^2/4 ] = 25.

Tương tự, K6, 4 = 24

K7, 3 = 21

K8, 2 = 16

K9, 1 = 9

Nếu n = 9, k5, 4 = [n2 / 4] = [92/4] = 20

Tương tự, K6, 3 = 18

K7, 2 = 14

K8, 1 = 8

'G' là một đồ thị lưỡng phân nếu 'G' không có chu trình nào có độ dài lẻ. Một trường hợp đặc biệt của đồ thị lưỡng cực là đồ thị hình sao.

Đồ thị sao

Một đồ thị hai bên hoàn chỉnh có dạng K1, n-1 là một đồ thị hình sao với n đỉnh. Đồ thị hình sao là một đồ thị lưỡng hợp hoàn chỉnh nếu một đỉnh đơn thuộc một tập hợp và tất cả các đỉnh còn lại thuộc tập hợp kia.

Thí dụ

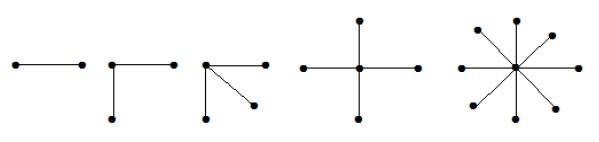
Trong các đồ thị trên, ngoài 'n' đỉnh, tất cả 'n-1' đều được nối với một đỉnh duy nhất. Do đó nó ở dạng K ¹ , ^n-1 là đồ thị hình sao.

Sự bổ sung của một đồ thị

Gọi 'G−' là một đồ thị đơn giản với một số đỉnh là của 'G' và một cạnh {U, V} nằm trong 'G−', nếu cạnh không có trong G. Điều đó có nghĩa là hai đỉnh kề nhau trong 'G−' nếu hai đỉnh không kề nhau trong G.

Nếu các cạnh tồn tại trong đồ thị I không có trong đồ thị II khác và nếu cả đồ thị I và đồ thị II được kết hợp với nhau để tạo thành một đồ thị hoàn chỉnh thì đồ thị I và đồ thị II được gọi là phần bù của nhau.

Thí dụ

Trong ví dụ sau, đồ thị-I có hai cạnh 'cd' và 'bd'. Đồ thị phần bù-II của nó có bốn cạnh.

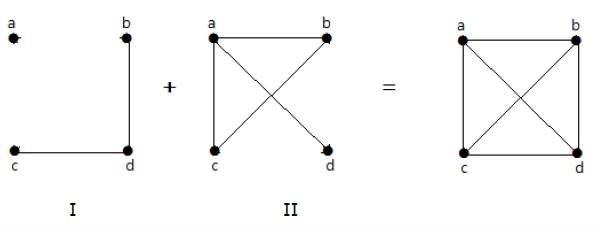
Lưu ý rằng các cạnh trong đồ thị-I không có trong đồ thị-II và ngược lại. Do đó, sự kết hợp của cả hai đồ thị sẽ cho một đồ thị hoàn chỉnh của 'n' đỉnh.

Note - Sự kết hợp của hai đồ thị bù nhau cho ra một đồ thị hoàn chỉnh.

Nếu 'G' là bất kỳ đồ thị đơn giản nào, thì

| E (G) | + | E ('G -') | = | E (Kn) |, trong đó n = số đỉnh trong đồ thị.