RADAR là một hệ thống phát hiện dựa trên điện từ hoạt động bằng cách bức xạ sóng điện từ và sau đó nghiên cứu tiếng vọng hoặc sóng phản xạ trở lại.

Hình thức đầy đủ của RADAR Là RAdio Detection And Rgóc cạnh. Phát hiện đề cập đến việc liệu mục tiêu có hiện diện hay không. Mục tiêu có thể đứng yên hoặc di động, tức là không đứng yên. Khoảng cách là khoảng cách giữa Radar và mục tiêu.

Radar có thể được sử dụng cho các ứng dụng khác nhau trên mặt đất, trên biển và trong không gian. Cácapplications của Radars được liệt kê bên dưới.

• Kiểm soát không lưu
• Tàu an toàn
• Cảm biến những nơi xa
• Ứng dụng quân sự

Trong bất kỳ ứng dụng nào của Radar, nguyên tắc cơ bản vẫn giống nhau. Bây giờ chúng ta hãy thảo luận về nguyên lý của radar.

Nguyên lý cơ bản của Radar

Radar được sử dụng để phát hiện các đối tượng và tìm vị trí của chúng. Chúng tôi có thể hiểubasic principle của Radar từ hình sau.

Như trong hình, Radar chủ yếu bao gồm một máy phát và một máy thu. Nó sử dụng cùng một Antenna để truyền và nhận tín hiệu. Chức năng củatransmitter là truyền tín hiệu Radar theo hướng của mục tiêu hiện diện.

Mục tiêu phản ánh tín hiệu nhận được này theo nhiều hướng khác nhau. Tín hiệu, được phản xạ trở lại Antenna nhận được bởireceiver.

Thuật ngữ của hệ thống radar

Sau đây là các thuật ngữ cơ bản, hữu ích trong hướng dẫn này.

• Range
• Tần số lặp lại xung
• Phạm vi rõ ràng tối đa
• Phạm vi tối thiểu

Bây giờ, chúng ta hãy thảo luận về từng thuật ngữ cơ bản này.

Phạm vi

Khoảng cách giữa Radar và mục tiêu được gọi là Range của mục tiêu hoặc đơn giản là phạm vi, R. Chúng ta biết rằng Radar truyền tín hiệu đến mục tiêu và theo đó mục tiêu sẽ gửi tín hiệu tiếng vọng tới Radar với tốc độ ánh sáng, C.

Đặt thời gian cần thiết để tín hiệu đi từ Radar đến mục tiêu và trở lại Radar là 'T'. Khoảng cách hai chiều giữa Radar và mục tiêu sẽ là 2R, vì khoảng cách giữa Radar và mục tiêu là R.

Bây giờ, sau đây là công thức cho Speed.

$$Speed= \frac{Distance}{Time}$$

$$\Rightarrow Distance=Speed\times Time$$

$$\Rightarrow 2R=C\times T$$

$$R=\frac{CT}{2}\:\:\:\:\:Equation\:1$$

Chúng tôi có thể tìm thấy range of the target bằng cách thay thế các giá trị của C & T trong Công thức 1.

Tần số lặp lại xung

Tín hiệu radar nên được truyền ở mọi xung đồng hồ. Khoảng thời gian giữa hai xung đồng hồ phải được chọn đúng cách sao cho tín hiệu tiếng vọng tương ứng với xung đồng hồ hiện tại phải được nhận trước xung đồng hồ tiếp theo. Một điển hìnhRadar wave form được hiển thị trong hình sau.

Như trong hình, Radar truyền tín hiệu tuần hoàn. Nó đang có một loạt các xung hình chữ nhật hẹp. Khoảng thời gian giữa các xung đồng hồ liên tiếp được gọi làpulse repetition time, $T_P$.

Biến thiên của thời gian lặp lại xung được gọi là pulse repetition frequency, $f_P$. Về mặt toán học, nó có thể được biểu diễn dưới dạng

$$f_P=\frac{1}{T_P}\:\:\:\:\:Equation\:2$$

Do đó, tần số lặp lại xung không là gì khác ngoài tần số mà Radar truyền tín hiệu.

Phạm vi rõ ràng tối đa

Chúng ta biết rằng tín hiệu Radar nên được truyền ở mọi xung đồng hồ. Nếu chúng ta chọn khoảng thời gian ngắn hơn giữa hai xung đồng hồ, thì tín hiệu tiếng vọng tương ứng với xung đồng hồ hiện tại sẽ được nhận sau xung đồng hồ tiếp theo. Do đó, phạm vi của mục tiêu dường như nhỏ hơn phạm vi thực tế.

Vì vậy, chúng ta phải chọn khoảng thời gian giữa hai xung đồng hồ sao cho tín hiệu tiếng vọng tương ứng với xung đồng hồ hiện tại sẽ được nhận trước khi xung đồng hồ tiếp theo bắt đầu. Sau đó, chúng tôi sẽ nhận được phạm vi thực sự của mục tiêu và nó còn được gọi là phạm vi rõ ràng tối đa của mục tiêu hoặc đơn giản,maximum unambiguous range.

Thay thế, $R=R_{un}$ và $T=T_P$ trong phương trình 1.

$$R_{un}=\frac{CT_P}{2}\:\:\:\:\:Equation\:3$$

Từ phương trình 2, chúng ta sẽ nhận được thời gian lặp lại xung, $T_P$ như nghịch đảo của tần số lặp lại xung, $f_P$. Mathematically, nó có thể được biểu thị là

$$T_P=\frac{1}{f_P}\:\:\:\:\:Equation\:4$$

Thay thế, phương trình 4 trong phương trình 3.

$$R_{un}=\frac{C\left ( \frac{1}{f_P} \right )}{2}$$

$$R_{un}=\frac{C}{2f_P}\:\:\:\:\:Equation\:5$$

Chúng ta có thể sử dụng Phương trình 3 hoặc Phương trình 5 để tính toán phạm vi rõ ràng tối đa của mục tiêu.

• Chúng tôi sẽ nhận được giá trị của phạm vi rõ ràng tối đa của mục tiêu, $R_{un}$ bằng cách thay thế các giá trị của $C$ và $T_P$ trong phương trình 3.

• Tương tự, chúng tôi sẽ nhận được giá trị của phạm vi rõ ràng tối đa của mục tiêu, $R_{un}$ bằng cách thay thế các giá trị của $C$ và $f_P$ trong phương trình 5.

Phạm vi tối thiểu

Chúng tôi sẽ nhận được minimum rangecủa mục tiêu, khi chúng ta coi thời gian cần thiết để tín hiệu tiếng vọng nhận được tại Radar sau khi tín hiệu được truyền từ Radar là độ rộng xung. Nó cũng được gọi là phạm vi ngắn nhất của mục tiêu.

Thay thế, $R=R_{min}$ và $T=\tau$ trong phương trình 1.

$$R_{min}=\frac{C\tau}{2}\:\:\:\:\:Equation\:6$$

Chúng tôi sẽ nhận được giá trị của phạm vi tối thiểu của mục tiêu, $R_{min}$ bằng cách thay thế các giá trị của $C$ và $\tau$ trong phương trình 6.

Phương trình phạm vi của radar rất hữu ích để biết phạm vi của mục tiêu theoretically. Trong chương này, chúng ta sẽ thảo luận về dạng chuẩn của phương trình dải Radar và sau đó sẽ thảo luận về hai dạng sửa đổi của phương trình dải Radar.

Chúng ta sẽ nhận được các dạng sửa đổi đó của phương trình dải Radar từ dạng chuẩn của phương trình dải Radar. Bây giờ, chúng ta hãy thảo luận về sự suy ra dạng chuẩn của phương trình phạm vi Radar.

Xác định phương trình phạm vi radar

Dạng chuẩn của phương trình phạm vi Radar còn được gọi là dạng đơn giản của phương trình phạm vi Radar. Bây giờ, chúng ta hãy suy ra dạng chuẩn của phương trình phạm vi Radar.

Chúng ta biết rằng power densitykhông là gì khác ngoài tỷ lệ giữa quyền lực và diện tích. Vì vậy, mật độ năng lượng,$P_{di}$ ở một khoảng cách xa, R từ Radar có thể được biểu diễn toán học dưới dạng:

$$P_{di}=\frac{P_t}{4\pi R^2}\:\:\:\:\:Equation\:1$$

Ở đâu,

$P_t$

Mật độ công suất trên là hợp lệ đối với một Anten đẳng hướng. Nói chung, các Radar sử dụng Anten định hướng. Do đó, mật độ công suất,$P_{dd}$ do định hướng Antenna sẽ -

$$P_{dd}=\frac{P_tG}{4\pi R^2}\:\:\:\:\:Equation\:2$$

Mục tiêu bức xạ công suất theo các hướng khác nhau từ công suất đầu vào nhận được. Lượng điện được phản xạ trở lại Radar phụ thuộc vào tiết diện của nó. Vì vậy, mật độ công suất$P_{de}$ của tín hiệu tiếng vọng tại Radar có thể được biểu diễn toán học như sau:

$$P_{de}=P_{dd}\left (\frac{\sigma}{4\pi R^2}\right )\:\:\:\:\:Equation\:3$$ Thay thế, Phương trình 2 trong Phương trình 3.

$$P_{de}=\left (\frac{P_tG}{4\pi R^2}\right )\left (\frac{\sigma}{4\pi R^2}\right )\:\:\:\:\:Equation\:4$$

Số lượng power, $P_r$ received bởi Radar phụ thuộc vào khẩu độ hiệu quả, $A_e$ của Anten nhận.

$$P_r=P_{de}A_e\:\:\:\:\:Equation\:5$$

Thay thế, phương trình 4 trong phương trình 5.

$$P_r=\left (\frac{P_tG}{4\pi R^2}\right )\left (\frac{\sigma}{4\pi R^2}\right )A_e$$

$$\Rightarrow P_r=\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 R^4}$$

$$\Rightarrow R^4=\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 P_r}$$

$$\Rightarrow R=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 P_r}\right ]^{1/4}\:\:\:\:\:Equation\:6$$

Dạng chuẩn của phương trình phạm vi radar

Nếu tín hiệu vọng lại có công suất nhỏ hơn công suất của tín hiệu phát hiện tối thiểu, thì Radar không thể phát hiện mục tiêu vì nó nằm ngoài giới hạn tối đa trong phạm vi của Radar.

Do đó, chúng ta có thể nói rằng phạm vi của mục tiêu được cho là phạm vi tối đa khi tín hiệu tiếng vọng nhận được có công suất bằng với công suất của tín hiệu có thể phát hiện tối thiểu. Chúng ta sẽ nhận được phương trình sau, bằng cách thay thế$R=R_{Max}$ và $P_r=S_{min}$ trong phương trình 6.

$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}\:\:\:\:\:Equation\:7$$

Phương trình 7 đại diện cho standard formcủa phương trình phạm vi Radar. Bằng cách sử dụng phương trình trên, chúng ta có thể tìm thấy phạm vi tối đa của mục tiêu.

Các dạng sửa đổi của phương trình phạm vi radar

Chúng tôi biết mối quan hệ sau đây giữa Gain của Antenna định hướng, $G$ và khẩu độ hiệu quả, $A_e$.

$$G=\frac{4\pi A_e}{\lambda^2}\:\:\:\:\:Equation\:8$$

Thay thế, phương trình 8 trong phương trình 7.

$$R_{Max}=\left [ \frac{P_t\sigma A_e}{\left ( 4\pi \right )^2S_{min}}\left ( \frac{4\pi A_e}{\lambda^2} \right ) \right ]^{1/4}$$

$$\Rightarrow R_{Max}=\left [\frac{P_tG\sigma {A_e}^2}{4\pi \lambda^2 S_{min}}\right ]^{1/4}\:\:\:\:\:Equation\:9$$

Phương trình 9 đại diện cho modified formcủa phương trình phạm vi Radar. Bằng cách sử dụng phương trình trên, chúng ta có thể tìm thấy phạm vi tối đa của mục tiêu.

Chúng ta sẽ nhận được mối quan hệ sau đây giữa khẩu độ hiệu quả, $A_e$ và Gain của Antenna định hướng, $G$ từ phương trình 8.

$$A_e=\frac{G\lambda^2}{4\pi}\:\:\:\:\:Equation\:10$$

Thay thế, phương trình 10 trong phương trình 7.

$$R_{Max}=\left [\frac{P_tG\sigma}{\left (4\pi\right )^2 S_{min}}(\frac{G\lambda^2}{4\pi})\right ]^{1/4}$$

$$\Rightarrow R_{Max}=\left [\frac{P_tG^2 \lambda^2 \sigma}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}\:\:\:\:\:Equation\:11$$

Phương trình 11 biểu diễn another modified form của phương trình phạm vi Radar. Bằng cách sử dụng phương trình trên, chúng ta có thể tìm thấy phạm vi tối đa của mục tiêu.

Note - Dựa trên dữ liệu đã cho, chúng ta có thể tìm phạm vi tối đa của mục tiêu bằng cách sử dụng một trong ba phương trình sau, cụ thể là

• Phương trình 7
• Phương trình 9
• Phương trình 11

Vấn đề ví dụ

Trong phần trước, chúng ta đã có các dạng chuẩn và sửa đổi của phương trình phạm vi Radar. Bây giờ, chúng ta hãy giải một vài vấn đề bằng cách sử dụng các phương trình đó.

Vấn đề 1

Tính toán maximum range of Radar cho các thông số kỹ thuật sau -

• Công suất đỉnh do Radar truyền, $P_t=250KW$
• Tăng Antenna truyền, $G=4000$
• Khẩu độ hiệu quả của Antenna nhận, $A_e=4\:m^2$
• Mặt cắt radar của mục tiêu, $\sigma=25\:m^2$
• Công suất của tín hiệu có thể phát hiện tối thiểu, $S_{min}=10^{-12}W$

Giải pháp

Chúng ta có thể sử dụng những thứ sau standard form của phương trình phạm vi Radar để tính toán phạm vi tối đa của Radar cho các thông số kỹ thuật nhất định.

$$R_{Max}=\left [\frac{P_tG \sigma A_e}{\left (4\pi \right )^2 S_{min}}\right ]^{1/4}$$

Substitute tất cả các tham số đã cho trong phương trình trên.

$$R_{Max}=\left [\frac{ \left ( 250\times 10^3 \right )\left ( 4000 \right )\left ( 25 \right )\left ( 4 \right )}{\left ( 4\pi \right )^2 \left ( 10^{-12} \right )} \right ]^{1/4}$$

$$\Rightarrow R_{Max}=158\:KM$$

Do đó, maximum range of Radar cho các thông số kỹ thuật nhất định là $158\:KM$.

Vấn đề 2

Tính toán maximum range of Radar cho các thông số kỹ thuật sau.

• Tần số hoạt động, $f=10GHZ$
• Công suất đỉnh do Radar truyền, $P_t=400KW$
• Khẩu độ hiệu quả của Antenna nhận, $A_e=5\:m^2$
• Mặt cắt radar của mục tiêu, $\sigma=30\:m^2$
• Công suất của tín hiệu có thể phát hiện tối thiểu, $S_{min}=10^{-10}W$

Giải pháp

Chúng tôi biết công thức sau đây cho operating wavelength, $\lambda$ về tần số hoạt động, f.

$$\lambda =\frac{C}{f}$$

Thay thế, $C=3\times 10^8m/sec$ và $f=10GHZ$ trong phương trình trên.

$$\lambda =\frac{3\times 10^8}{10\times 10^9}$$

$$\Rightarrow \lambda=0.03m$$

Nên operating wavelength,$\lambda$ bằng $0.03m$, khi tần số hoạt động, $f$ Là $10GHZ$.

Chúng ta có thể sử dụng những thứ sau modified form của phương trình phạm vi Radar để tính toán phạm vi tối đa của Radar cho các thông số kỹ thuật nhất định.

$$R_{Max}=\left [\frac{P_t \sigma {A_e}^2}{4\pi \lambda^2 S_{min}}\right ]^{1/4}$$

Substitute, các tham số đã cho trong phương trình trên.

$$R_{Max}=\left [ \frac{\left ( 400\times 10^3 \right )\left ( 30 \right )\left ( 5^2 \right )}{4\pi\left ( 0.003 \right )^2\left ( 10 \right )^{-10}} \right ]^{1/4}$$

$$\Rightarrow R_{Max}=128KM$$

Do đó, maximum range of Radar cho các thông số kỹ thuật nhất định là $128\:KM$.

Các yếu tố ảnh hưởng đến hiệu suất của Radar được gọi là hệ số hiệu suất của Radar. Trong chương này, chúng ta hãy thảo luận về những yếu tố đó. Chúng tôi biết rằng những điều saustandard form của phương trình phạm vi Radar, rất hữu ích để tính toán phạm vi tối đa của Radar cho các thông số kỹ thuật nhất định.

$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$

Ở đâu,

$P_t$ là công suất đỉnh do Radar truyền

$G$ là lợi ích của việc truyền Antenna

$\sigma$ là tiết diện Radar của mục tiêu

$A_e$ là khẩu độ hiệu quả của Antenna nhận

$S_{min}$ là sức mạnh của tín hiệu có thể phát hiện tối thiểu

Từ phương trình trên, chúng ta có thể kết luận rằng conditions nên được xem xét để có được phạm vi hoạt động của Radar là tối đa.

• Công suất đỉnh do Radar truyền $P_t$ nên cao.
• Đạt được Antenna truyền $G$ nên cao.
• Mặt cắt radar của mục tiêu $\sigma$ nên cao.
• Khẩu độ hiệu quả của Antenna nhận $A_e$ nên cao.
• Công suất của tín hiệu có thể phát hiện tối thiểu $S_{min}$ nên thấp.

Rất khó để dự đoán phạm vi của mục tiêu từ dạng chuẩn của phương trình phạm vi Radar. Điều này có nghĩa là, mức độ chính xác được cung cấp bởi phương trình phạm vi của Radar về phạm vi của mục tiêu sẽ ít hơn. Bởi vì, các tham số như tiết diện Radar của mục tiêu,$\sigma$ và tín hiệu có thể phát hiện tối thiểu, $S_{min}$ Chúng tôi statistical in nature.

Tín hiệu có thể phát hiện tối thiểu

Nếu tín hiệu tiếng vọng có công suất tối thiểu, việc phát hiện tín hiệu đó bằng Radar được gọi là minimum detectable signal. Điều này có nghĩa là, Radar không thể phát hiện ra tín hiệu dội âm nếu tín hiệu đó có công suất nhỏ hơn công suất tối thiểu.

Nói chung, Radar nhận được tín hiệu tiếng vang cùng với tiếng ồn. Nếu giá trị ngưỡng được sử dụng để phát hiện sự hiện diện của mục tiêu từ tín hiệu nhận được, thì phát hiện đó được gọi làthreshold detection.

Chúng ta phải chọn giá trị ngưỡng thích hợp dựa trên cường độ của tín hiệu được phát hiện.

• Giá trị ngưỡng cao nên được chọn khi cường độ của tín hiệu được phát hiện cao để loại bỏ tín hiệu nhiễu không mong muốn có trong nó.

• Tương tự, giá trị ngưỡng thấp nên được chọn khi cường độ của tín hiệu được phát hiện thấp.

Sau figure minh họa khái niệm này -

A typical waveformcủa máy thu Radar được hiển thị trong hình trên. Trục x và trục y lần lượt thể hiện thời gian và điện áp. Giá trị rms của nhiễu và giá trị ngưỡng được biểu thị bằng các đường chấm trong hình trên.

Chúng tôi đã xem xét ba điểm A, B & C trong hình trên để xác định các phát hiện hợp lệ và phát hiện thiếu.

• Giá trị của tín hiệu tại điểm A lớn hơn giá trị ngưỡng. Do đó, nó là mộtvalid detection.

• Giá trị của tín hiệu tại điểm B bằng giá trị ngưỡng. Do đó, nó là mộtvalid detection.

• Mặc dù giá trị của tín hiệu tại điểm C gần với giá trị ngưỡng hơn, nó là missing detection. Bởi vì, giá trị của tín hiệu tại điểm C nhỏ hơn giá trị ngưỡng.

Vì vậy, các điểm, A & B là các phát hiện hợp lệ. Trong khi đó, điểm C là một phát hiện thiếu.

Máy thu tiếng ồn

Nếu máy thu tạo ra một thành phần tạp âm vào tín hiệu nhận được tại máy thu, thì loại tạp âm đó được gọi là tạp âm máy thu. Cácreceiver noiselà một thành phần không mong muốn; chúng ta nên cố gắng loại bỏ nó bằng một số biện pháp phòng ngừa.

Tuy nhiên, tồn tại một loại tiếng ồn được gọi là tiếng ồn nhiệt. Nó xảy ra do chuyển động nhiệt của các electron dẫn. Về mặt toán học, chúng ta có thể viếtthermal noise power, $N_i$ được sản xuất tại máy thu như -

$$N_i=KT_oB_n$$

Ở đâu,

$K$ là hằng số Boltzmann và nó bằng $1.38\times 10^{-23}J/deg$

$T_o$ là nhiệt độ tuyệt đối và nó bằng $290^0K$

$B_n$ là độ rộng băng tần của máy thu

Hình bằng khen

Các Figure of Merit, F không là gì ngoài tỷ lệ SNR đầu vào, $(SNR)_i$ và xuất ra SNR, $(SNR)_o$. Về mặt toán học, nó có thể được biểu diễn dưới dạng:

$$F=\frac{(SNR)_i}{(SNR)_o}$$

$$\Rightarrow F=\frac{S_i/N_i}{S_o/N_o}$$

$$\Rightarrow F=\frac{N_oS_i}{N_iS_o}$$

$$\Rightarrow S_i=\frac{FN_iS_o}{N_o}$$

Thay thế, $N_i=KT_oB_n$ trong phương trình trên.

$$\Rightarrow S_i=FKT_oB_n\left ( \frac{S_o}{N_o}\right )$$

Công suất tín hiệu đầu vào sẽ có giá trị nhỏ nhất, khi SNR đầu ra có giá trị nhỏ nhất.

$$\Rightarrow S_{min}=FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min}$$

Thay thế, ở trên $S_{min}$ ở dạng chuẩn sau của phương trình phạm vi Radar.

$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$

$$\Rightarrow R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min}}\right ]^{1/4}$$

Từ phương trình trên, chúng ta có thể kết luận rằng conditions nên được xem xét để có được phạm vi hoạt động của Radar là tối đa.

• Công suất đỉnh do Radar truyền, $P_t$ nên cao.
• Đạt được Antenna truyền $G$ nên cao.
• Mặt cắt radar của mục tiêu $\sigma$ nên cao.
• Khẩu độ hiệu quả của Antenna nhận $A_e$ nên cao.
• Con số khen thưởng F nên thấp.
• Băng thông máy thu $B_n$ nên thấp.

Trong chương này, chúng ta sẽ thảo luận ngắn gọn về các loại Radar khác nhau. Chương này cung cấp thông tin ngắn gọn về các loại Radar. Radar có thể được phân loại thành các loại sautwo types dựa trên loại tín hiệu mà Radar có thể hoạt động.

• Radar xung
• Radar sóng liên tục

Bây giờ, chúng ta hãy thảo luận về hai loại Radars này.

Radar xung

Radar, hoạt động với tín hiệu xung được gọi là Pulse Radar. Radar xung có thể được phân loại thành hai loại sau đây dựa trên loại mục tiêu mà nó phát hiện.

• Radar xung cơ bản
• Rađa chỉ thị mục tiêu di chuyển

Bây giờ chúng ta hãy thảo luận ngắn gọn về hai Radar.

Radar xung cơ bản

Radar, hoạt động với tín hiệu xung để phát hiện các mục tiêu đứng yên, được gọi là Basic Pulse Radarhay đơn giản là Pulse Radar. Nó sử dụng một Antenna cho cả tín hiệu truyền và nhận với sự trợ giúp của Duplexer.

Ăng-ten sẽ truyền một tín hiệu xung ở mỗi xung đồng hồ. Khoảng thời gian giữa hai xung đồng hồ phải được chọn sao cho nhận được tín hiệu tiếng vọng tương ứng với xung đồng hồ hiện tại trước xung đồng hồ tiếp theo.

Rađa chỉ thị mục tiêu di chuyển

Radar, hoạt động với tín hiệu xung để phát hiện các mục tiêu không đứng yên, được gọi là Radar Chỉ thị Mục tiêu Di chuyển hoặc đơn giản là, MTI Radar. Nó sử dụng Antenna đơn cho cả việc truyền và nhận tín hiệu với sự trợ giúp của Duplexer.

MTI Radar sử dụng nguyên tắc Doppler effect để phân biệt các mục tiêu không đứng yên với các vật thể đứng yên.

Radar sóng liên tục

Radar, hoạt động với tín hiệu hoặc sóng liên tục được gọi là Continuous Wave Radar. Họ sử dụng Hiệu ứng Doppler để phát hiện các mục tiêu không cố định. Radar sóng liên tục có thể được phân loại thành hai loại sau.

• Radar sóng liên tục không điều chế
• Radar sóng liên tục được điều chế tần số

Bây giờ, chúng ta hãy thảo luận ngắn gọn về hai Radar.

Radar sóng liên tục không điều chế

Radar, hoạt động với tín hiệu liên tục (sóng) để phát hiện mục tiêu không đứng yên được gọi là Radar sóng liên tục không điều chế hay đơn giản là CW Radar. Nó còn được gọi là CW Doppler Radar.

Radar này yêu cầu hai Anten. Trong hai anten này, một anten dùng để truyền tín hiệu và anten còn lại dùng để thu tín hiệu. Nó chỉ đo tốc độ của mục tiêu chứ không đo được khoảng cách của mục tiêu từ Radar.

Radar sóng liên tục được điều chế tần số

Nếu CW Doppler Radar sử dụng Điều chế tần số, thì Radar đó được gọi là Sóng liên tục được điều chế tần số (FMCW)Radar hoặc FMCW Doppler Radar. Nó còn được gọi là Radar điều biến tần số sóng liên tục hoặc Radar CWFM.

Radar này yêu cầu hai Anten. Trong đó, một Antenna được sử dụng để truyền tín hiệu và Antenna còn lại được sử dụng để nhận tín hiệu. Nó không chỉ đo tốc độ của mục tiêu mà còn đo khoảng cách của mục tiêu với Radar.

Trong các chương tiếp theo, chúng ta sẽ thảo luận chi tiết về hoạt động của tất cả các Radar này.

Radar, hoạt động với tín hiệu xung để phát hiện mục tiêu tĩnh được gọi là Radar xung cơ bản hoặc đơn giản, Pulse Radar. Trong chương này, chúng ta hãy thảo luận về hoạt động của Radar xung.

Sơ đồ khối của Radar xung

Pulse Radar sử dụng một Antenna để truyền và nhận tín hiệu với sự hỗ trợ của Duplexer. Sau đây làblock diagram của Radar xung -

Bây giờ chúng ta hãy xem function của mỗi khối Radar xung -

• Pulse Modulator - Nó tạo ra một tín hiệu được điều chế xung và nó được đưa vào Máy phát.

• Transmitter - Nó truyền tín hiệu được điều chế xung, là một nhóm các xung lặp đi lặp lại.

• Duplexer- Là công tắc viba, kết nối luân phiên Antenna với cả phần phát và phần thu. Ăng-ten truyền tín hiệu được điều chế xung, khi bộ song công kết nối Ăng-ten với máy phát. Tương tự, tín hiệu nhận được bởi Ăng-ten sẽ được đưa đến Bộ khuếch đại RF có độ ồn thấp, khi bộ song công kết nối Ăng-ten với Bộ khuếch đại RF có độ ồn thấp.

• Low Noise RF Amplifier- Nó khuếch đại tín hiệu RF yếu, được nhận bởi Antenna. Đầu ra của bộ khuếch đại này được kết nối với Mixer.

• Local Oscillator- Nó tạo ra một tín hiệu có tần số ổn định. Đầu ra của Bộ tạo dao động cục bộ được kết nối với Bộ trộn.

• Mixer- Chúng tôi biết rằng Mixer có thể tạo ra cả tổng và sự khác biệt của các tần số được áp dụng cho nó. Trong đó, sự khác biệt của các tần số sẽ thuộc loại Tần số trung gian (IF).

• IF Amplifier- Bộ khuếch đại IF khuếch đại tín hiệu Tần số trung gian (IF). Bộ khuếch đại IF được hiển thị trong hình chỉ cho phép Tần số trung gian, được lấy từ Bộ trộn và khuếch đại nó. Nó cải thiện Tỷ lệ tín hiệu trên nhiễu ở đầu ra.

• Detector - Nó giải điều chế tín hiệu thu được ở đầu ra của Bộ khuếch đại IF.

• Video Amplifier - Như tên cho thấy, nó khuếch đại tín hiệu video, thu được ở đầu ra của máy dò.

• Display - Nói chung, nó hiển thị tín hiệu video khuếch đại trên màn hình CRT.

Trong chương này, chúng ta đã thảo luận về cách thức hoạt động của Radar xung và cách nó hữu ích để phát hiện các mục tiêu đứng yên. Trong các chương tiếp theo của chúng ta, chúng ta sẽ thảo luận về Radar, rất hữu ích để phát hiện các mục tiêu không cố định.

Trong chương này, chúng ta sẽ tìm hiểu về Hiệu ứng Doppler trong Hệ thống Radar.

Nếu mục tiêu không đứng yên, thì sẽ có sự thay đổi tần số của tín hiệu được truyền từ Radar và tín hiệu đó sẽ được nhận bởi Radar. Hiệu ứng này được gọi làDoppler effect.

Theo hiệu ứng Doppler, chúng ta sẽ nhận được hai trường hợp có thể xảy ra sau:

• Các frequency của tín hiệu nhận được sẽ increase, khi mục tiêu di chuyển theo hướng của Radar.

• Các frequency của tín hiệu nhận được sẽ decrease, khi mục tiêu di chuyển khỏi Radar.

Bây giờ, chúng ta hãy suy ra công thức cho tần số Doppler.

Xác định tần số Doppler

Khoảng cách giữa Radar và mục tiêu là không có gì khác ngoài Range của mục tiêu hoặc đơn giản là phạm vi, R. Do đó, tổng khoảng cách giữa Radar và mục tiêu trong đường liên lạc hai chiều sẽ là 2R, vì Radar truyền tín hiệu đến mục tiêu và theo đó mục tiêu sẽ gửi tín hiệu tiếng vọng tới Radar.

Nếu $\lambda$ là một độ dài sóng, khi đó số độ dài sóng N có trong đường truyền thông tin hai chiều giữa Radar và mục tiêu sẽ bằng $2R/\lambda$.

Chúng tôi biết rằng một chiều dài sóng $\lambda$ tương ứng với một chuyến du ngoạn góc của $2\pi$rađian. Nêntotal angle of excursion được tạo ra bởi sóng điện từ trong quá trình liên lạc hai chiều giữa Radar và mục tiêu sẽ bằng $4\pi R/\lambda$ rađian.

Sau đây là công thức toán học cho angular frequency, $\omega$ -

$$\omega=2\pi f\:\:\:\:\:Equation\:1$$

Phương trình sau đây cho thấy mối quan hệ toán học giữa tần số góc $\omega$ và góc pha $\phi$ -

$$\omega=\frac{d\phi }{dt}\:\:\:\:\:Equation\:2$$

Equate các số hạng bên phải của phương trình 1 và phương trình 2 vì các số hạng bên trái của hai phương trình đó giống nhau.

$$2\pi f=\frac{d\phi }{dt}$$

$$\Rightarrow f =\frac{1}{2\pi}\frac{d\phi }{dt}\:\:\:\:\:Equation\:3$$

Substitute,$f=f_d$ và $\phi=4\pi R/\lambda$ trong phương trình 3.

$$f_d =\frac{1}{2\pi}\frac{d}{dt}\left ( \frac{4\pi R}{\lambda} \right )$$

$$\Rightarrow f_d =\frac{1}{2\pi}\frac{4\pi}{\lambda}\frac{dR}{dt}$$

$$\Rightarrow f_d =\frac{2V_r}{\lambda}\:\:\:\:\:Equation\:4$$

Ở đâu,

$f_d$ là tần số Doppler

$V_r$ là vận tốc tương đối

Chúng ta có thể tìm thấy giá trị của tần số Doppler $f_d$ bằng cách thay thế các giá trị của $V_r$ và $\lambda$ trong phương trình 4.

Substitute, $\lambda=C/f$ trong phương trình 4.

$$f_d =\frac{2V_r}{C/f}$$

$$\Rightarrow f_d =\frac{2V_rf}{C}\:\:\:\:\:Equation\:5$$

Ở đâu,

$f$ là tần số của tín hiệu truyền đi

$C$ là tốc độ ánh sáng và nó bằng $3\times 10^8m/sec$

Chúng ta có thể tìm thấy giá trị của tần số Doppler, $f_d$ bằng cách thay thế các giá trị của $V_r,f$ và $C$ trong phương trình 5.

Note - Cả phương trình 4 và phương trình 5 đều hiển thị các công thức của tần số Doppler, $f_d$. Chúng ta có thể sử dụng phương trình 4 hoặc phương trình 5 để tìmDoppler frequency, $f_d$ dựa trên dữ liệu đã cho.

Vấn đề ví dụ

Nếu Radar hoạt động ở tần số $5GHZ$, sau đó tìm Doppler frequency của một máy bay chuyển động với tốc độ 100KMph.

Giải pháp

Được,

Tần số của tín hiệu đã truyền, $f=5GHZ$

Tốc độ của máy bay (mục tiêu), $V_r=100KMph$

$$\Rightarrow V_r=\frac{100\times 10^3}{3600}m/sec$$

$$\Rightarrow V_r=27.78m/sec$$

Chúng tôi đã chuyển đổi tốc độ nhất định của máy bay (mục tiêu), tính bằng KMph thành m / giây tương đương của nó.

Chúng ta biết rằng, tốc độ ánh sáng, $C=3\times 10^8m/sec$

Bây giờ, sau đây là formula for Doppler frequency -

$$f_d=\frac{2Vrf}{C}$$

Substitute các giá trị của ð ?? '‰ ð ??' Ÿ, $V_r,f$ và $C$ trong phương trình trên.

$$\Rightarrow f_d=\frac{2\left ( 27.78 \right )\left ( 5\times 10^9 \right )}{3\times 10^8}$$

$$\Rightarrow f_d=926HZ$$

Do đó, giá trị của Doppler frequency, $f_d$ Là $926HZ$ cho các thông số kỹ thuật nhất định.

Radar cơ bản sử dụng cùng một Antenna cho cả việc truyền và nhận tín hiệu. Chúng ta có thể sử dụng loại Radar này khi mục tiêu đứng yên, tức là không di chuyển và / hoặc khi Radar đó có thể hoạt động với tín hiệu xung.

Radar, hoạt động với tín hiệu liên tục (sóng) để phát hiện mục tiêu không đứng yên, được gọi là Radar sóng liên tục hoặc đơn giản là CW Radar. Radar này yêu cầu hai Anten. Trong đó, một Antenna được sử dụng để truyền tín hiệu và Antenna còn lại được sử dụng để nhận tín hiệu.

Sơ đồ khối của Radar CW

Chúng ta biết rằng CW Doppler Radar có chứa hai Anten - Anten truyền và Anten nhận. Hình sau cho thấyblock diagram của CW Radar -

Sơ đồ khối của CW Doppler Radar chứa một tập hợp các khối và function của mỗi khối được đề cập dưới đây.

• CW Transmitter - Nó tạo ra một tín hiệu tương tự có tần số $f_o$. Đầu ra của CW Transmitter được kết nối với cả Antenna phát và Mixer-I.

• Local Oscillator - Nó tạo ra một tín hiệu có tần số $f_l$. Đầu ra của Local Oscillator được kết nối với Mixer-I.

• Mixer-I- Mixer có thể tạo ra cả tổng và sự khác biệt của các tần số được áp dụng cho nó. Các tín hiệu có tần số$f_o$ và $f_l$được áp dụng cho Mixer-I. Vì vậy, Mixer-I sẽ tạo ra đầu ra có tần số$f_o+f_l$ hoặc là $f_o−f_l$.

• Side Band Filter- Như tên cho thấy, bộ lọc dải bên cho phép một tần số dải bên cụ thể - tần số dải bên trên hoặc tần số dải bên dưới. Bộ lọc dải bên được hiển thị trong hình trên chỉ tạo ra tần số dải phía trên, tức là$f_o+f_l$.

• Mixer-II- Mixer có thể tạo ra cả tổng và sự khác biệt của các tần số được áp dụng cho nó. Các tín hiệu có tần số$f_o+f_l$ và $f_o\pm f_d$được áp dụng cho Mixer-II. Vì vậy, Mixer-II sẽ tạo ra đầu ra có tần số 2$f_o+f_l\pm f_d$ hoặc là $f_l\pm f_d$.

• IF Amplifier- Bộ khuếch đại IF khuếch đại tín hiệu Tần số trung gian (IF). Bộ khuếch đại IF được hiển thị trong hình chỉ cho phép Tần số trung gian,$f_l\pm f_d$ và khuếch đại nó.

• Detector - Nó phát hiện tín hiệu có tần số Doppler, $f_d$.

• Doppler Amplifier - Như tên cho thấy, bộ khuếch đại Doppler khuếch đại tín hiệu, có tần số Doppler, $f_d$.

• Indicator - Nó cho biết thông tin liên quan đến vận tốc tương đối và liệu mục tiêu là hướng đến hay hướng đi.

CW Doppler Radars cho phép đo chính xác relative velocities. Do đó, chúng được sử dụng hầu hết, trong đó thông tin về vận tốc quan trọng hơn phạm vi thực tế.

Nếu CW Doppler Radar sử dụng Điều chế tần số, thì Radar đó được gọi là FMCW Doppler Radar hoặc đơn giản, FMCW Radar. Nó còn được gọi là Radar điều biến tần số sóng liên tục hoặc Radar CWFM. Nó không chỉ đo tốc độ của mục tiêu mà còn đo khoảng cách của mục tiêu với Radar.

Sơ đồ khối của FMCW Radar

FMCW Radar chủ yếu được sử dụng như Radar Altimeter để đo độ cao chính xác khi máy bay hạ cánh. Hình sau cho thấyblock diagram của FMCW Radar -

FMCW Radarchứa hai Anten - Anten phát và Anten nhận như trong hình. Anten phát truyền tín hiệu và Anten thu nhận tín hiệu dội lại.

Sơ đồ khối của FMCW Radar trông tương tự như sơ đồ khối của CW Radar. Nó chứa một số khối sửa đổi và một số khối khác ngoài các khối có trong sơ đồ khối của CW Radar. Cácfunction của mỗi khối FMCW Radar được đề cập bên dưới.

• FM Modulator - Nó tạo ra tín hiệu được điều chế tần số (FM) có tần số thay đổi, $f_o\left (t \right )$ và nó được áp dụng cho máy phát FM.

• FM Transmitter- Nó truyền tín hiệu FM với sự trợ giúp của truyền Antenna. Đầu ra của Máy phát FM cũng được kết nối với Mixer-I.

• Local Oscillator- Nói chung, Bộ tạo dao động cục bộ được sử dụng để tạo ra tín hiệu RF. Tuy nhiên, ở đây nó được sử dụng để tạo ra tín hiệu có Tần số trung gian,$f_{IF}$. Đầu ra của Local Oscillator được kết nối với cả Mixer-I và Balanced Detector.

• Mixer-I- Mixer có thể tạo ra cả tổng và sự khác biệt của các tần số được áp dụng cho nó. Các tín hiệu có tần số$f_o\left (t \right )$ và $f_{IF}$được áp dụng cho Mixer-I. Vì vậy, Mixer-I sẽ tạo ra đầu ra có tần số$f_o\left (t \right )+f_{IF}$ hoặc là $f_o\left (t \right )-f_{IF}$.

• Side Band Filter- Nó chỉ cho phép một tần số dải bên, tức là tần số dải bên trên hoặc tần số dải bên dưới. Bộ lọc dải bên hiển thị trong hình chỉ tạo ra tần số dải bên thấp hơn. I E,$f_o\left (t \right )-f_{IF}$.

• Mixer-II- Mixer có thể tạo ra cả tổng và sự khác biệt của các tần số được áp dụng cho nó. Các tín hiệu có tần số$f_o\left (t \right )-f_{IF}$ và $f_o\left (t-T \right )$được áp dụng cho Mixer-II. Vì vậy, Mixer-II sẽ tạo ra đầu ra có tần số$f_o\left (t-T \right )+f_o\left (t \right )-f_{IF}$ hoặc là $f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$.

• IF Amplifier- Bộ khuếch đại IF khuếch đại tín hiệu Tần số trung gian (IF). Bộ khuếch đại IF thể hiện trong hình sẽ khuếch đại tín hiệu có tần số$f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$. Tín hiệu khuếch đại này được áp dụng làm đầu vào cho bộ tách sóng Cân bằng.

• Balanced Detector - Nó được sử dụng để tạo ra tín hiệu đầu ra có tần số $f_o\left (t-T \right )-f_o\left (t \right )$ từ hai tín hiệu đầu vào được áp dụng, có tần số $f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$ và $f_{IF}$. Đầu ra của bộ dò cân bằng được sử dụng làm đầu vào cho Bộ khuếch đại tần số thấp.

• Low Frequency Amplifier- Nó khuếch đại đầu ra của máy dò cân bằng đến mức cần thiết. Đầu ra của Bộ khuếch đại tần số thấp được áp dụng cho cả bộ đếm tần số chuyển mạch và bộ đếm tần số trung bình.

• Switched Frequency Counter - Nó rất hữu ích để lấy giá trị của vận tốc Doppler.

• Average Frequency Counter - Nó rất hữu ích để lấy giá trị của Phạm vi.

Nếu Radar được sử dụng để phát hiện mục tiêu di động, thì Radar sẽ chỉ nhận được tín hiệu tiếng vọng do mục tiêu di động đó. Tín hiệu tiếng vọng này là tín hiệu mong muốn. Tuy nhiên, trong các ứng dụng thực tế, Radar nhận tín hiệu dội lại do các vật thể đứng yên bên cạnh tín hiệu dội âm do mục tiêu chuyển động đó.

Các tín hiệu dội lại do các vật thể (địa điểm) đứng yên như đất liền và biển gọi là cluttersvì đây là những tín hiệu không mong muốn. Do đó, chúng ta phải chọn Radar sao cho nó chỉ xem xét tín hiệu tiếng vọng do mục tiêu có thể di chuyển được chứ không phải tín hiệu hỗn hợp.

Với mục đích này, Radar sử dụng nguyên lý của Hiệu ứng Doppler để phân biệt các mục tiêu không đứng yên với các vật thể đứng yên. Loại Radar này được gọi là Radar chỉ thị mục tiêu di chuyển hoặc đơn giản làMTI Radar.

Dựa theo Doppler effect, tần số của tín hiệu nhận được sẽ tăng lên nếu mục tiêu đang di chuyển theo hướng của Radar. Tương tự, tần số của tín hiệu nhận được sẽ giảm nếu mục tiêu đang di chuyển ra khỏi Radar.

Các loại rađa MTI

Chúng tôi có thể phân loại các Radar MTI thành các loại sau two types dựa trên loại máy phát đã được sử dụng.

• Radar MTI với Bộ phát khuếch đại công suất
• Radar MTI với máy phát dao động công suất

Bây giờ, chúng ta hãy thảo luận về hai Radar MTI này từng cái một.

Radar MTI với Bộ phát khuếch đại công suất

MTI Radar sử dụng Antenna đơn cho cả việc truyền và nhận tín hiệu với sự trợ giúp của Duplexer. Cácblock diagram của MTI Radar với bộ phát khuếch đại công suất được hiển thị trong hình sau.

Các function của mỗi khối MTI Radar với bộ phát khuếch đại công suất được đề cập dưới đây.

• Pulse Modulator - Nó tạo ra một tín hiệu được điều chế xung và nó được áp dụng cho Bộ khuếch đại công suất.

• Power Amplifier - Nó khuếch đại các mức công suất của tín hiệu điều chế xung.

• Local Oscillator - Nó tạo ra một tín hiệu có tần số ổn định $f_l$. Do đó, nó còn được gọi là Bộ tạo dao động cục bộ ổn định. Đầu ra của Bộ tạo dao động cục bộ được áp dụng cho cả Mixer-I và Mixer-II.

• Coherent Oscillator - Nó tạo ra một tín hiệu có Tần số trung gian, $f_c$. Tín hiệu này được sử dụng làm tín hiệu tham chiếu. Đầu ra của Bộ tạo dao động mạch lạc được áp dụng cho cả Bộ trộn-I và Bộ dò pha.

• Mixer-I- Mixer có thể tạo ra tổng hoặc chênh lệch của các tần số được áp dụng cho nó. Các tín hiệu có tần số$f_l$ và $f_c$được áp dụng cho Mixer-I. Ở đây, Mixer-I được sử dụng để tạo ra đầu ra, có tần số$f_l+f_c$.

• Duplexer- Là công tắc viba, kết nối Anten với phần phát hoặc phần thu tùy theo yêu cầu. Ăng-ten truyền tín hiệu có tần số$f_l+f_c$khi bộ song công kết nối Antenna với bộ khuếch đại công suất. Tương tự, Antenna nhận tín hiệu có tần số$f_l+f_c\pm f_d$ khi bộ song công kết nối Antenna với Mixer-II.

• Mixer-II- Mixer có thể tạo ra tổng hoặc chênh lệch của các tần số được áp dụng cho nó. Các tín hiệu có tần số$f_l+f_c\pm f_d$ và $f_l$được áp dụng cho Mixer-II. Ở đây, Mixer-II được sử dụng để tạo ra đầu ra có tần số$f_c\pm f_d$.

• IF Amplifier- Bộ khuếch đại IF khuếch đại tín hiệu Tần số trung gian (IF). Bộ khuếch đại IF thể hiện trong hình sẽ khuếch đại tín hiệu có tần số$f_c+f_d$. Tín hiệu khuếch đại này được áp dụng làm đầu vào cho bộ tách sóng Pha.

Phase Detector - Nó được sử dụng để tạo ra tín hiệu đầu ra có tần số $f_d$ từ hai tín hiệu đầu vào được áp dụng, có tần số $f_c+f_d$ và $f_c$. Đầu ra của máy dò pha có thể được kết nối với bộ hủy dòng trễ.

Radar MTI với máy phát dao động công suất

Sơ đồ khối của MTI Radar với bộ phát dao động công suất trông tương tự như sơ đồ khối của MTI Radar với bộ phát bộ khuếch đại công suất. Các khối tương ứng với phần thu sẽ giống nhau trong cả hai sơ đồ khối. Trong khi đó, các khối tương ứng với phần máy phát có thể khác nhau trong cả hai sơ đồ khối.

Các block diagram của Radar MTI với bộ phát dao động công suất được thể hiện trong hình sau.

Như trong hình, MTI Radar sử dụng Antenna duy nhất cho cả việc truyền và nhận tín hiệu với sự hỗ trợ của Duplexer. Cácoperation của MTI Radar với máy phát dao động công suất được đề cập dưới đây.

• Đầu ra của Magnetron Oscillator và đầu ra của Local Oscillator được áp dụng cho Mixer-I. Điều này sẽ tạo ra mộtIF signal, pha có liên quan trực tiếp đến pha của tín hiệu được truyền.

• Đầu ra của Mixer-I được áp dụng cho Bộ tạo dao động kết hợp. Do đó, pha của đầu ra Bộ dao động mạch lạc sẽ làlockedsang pha của tín hiệu IF. Điều này có nghĩa là, pha của đầu ra Bộ dao động mạch lạc cũng sẽ liên quan trực tiếp đến pha của tín hiệu được truyền.

• Vì vậy, đầu ra của Bộ dao động mạch lạc có thể được sử dụng làm tín hiệu tham chiếu để so sánh tín hiệu tiếng vọng nhận được với tín hiệu truyền tương ứng bằng cách sử dụng phase detector.

Các tác vụ trên sẽ được lặp lại cho mọi tín hiệu mới được truyền đi.

Hệ thống rađa - Bộ hủy đường truyền trễ

Trong chương này, chúng ta sẽ tìm hiểu về Bộ hủy dòng trễ trong Hệ thống Radar. Như tên cho thấy, đường trễ giới thiệu một lượng thời gian trễ nhất định. Vì vậy, dòng trễ chủ yếu được sử dụng trong bộ hủy dòng trễ để giới thiệu mộtdelay của thời gian lặp lại xung.

Delay line cancellerlà một bộ lọc, loại bỏ các thành phần DC của tín hiệu tiếng vọng nhận được từ các mục tiêu tĩnh. Điều này có nghĩa là, nó cho phép các thành phần AC của tín hiệu tiếng vọng nhận được từ các mục tiêu không đứng yên, tức là các mục tiêu chuyển động.

Các loại trình hủy dòng trễ

Bộ hủy dòng trễ có thể được phân loại như sau two types dựa trên số lượng đường trễ có trong nó.

• Bộ hủy dòng trễ đơn
• Bộ hủy dòng trễ kép

Trong các phần tiếp theo của chúng tôi, chúng tôi sẽ thảo luận thêm về hai trình hủy dòng trễ này.

Bộ hủy dòng trễ đơn

Sự kết hợp của một đường trễ và một bộ trừ được gọi là bộ hủy dòng trễ. Nó còn được gọi là bộ hủy dòng trễ đơn. Cácblock diagram của bộ thu MTI với bộ hủy dòng trễ duy nhất được hiển thị trong hình bên dưới.

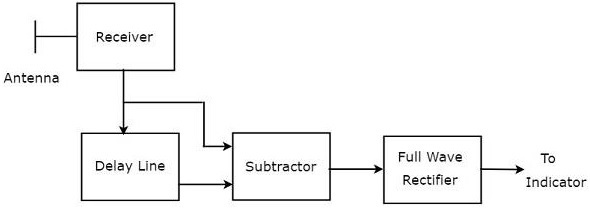
Chúng tôi có thể viết mathematical equation của tín hiệu tiếng vọng nhận được sau hiệu ứng Doppler là -

$$V_1=A\sin\left [ 2\pi f_dt-\phi_0 \right ]\:\:\:\:\:Equation\:1$$

Ở đâu,

A là biên độ của tín hiệu video

$f_d$ là tần số Doppler

$\phi_o$ là sự dịch chuyển pha và nó bằng $4\pi f_tR_o/C$

Chúng tôi sẽ nhận được output of Delay line canceller, Bằng cách thay thế $t$ bởi $t-T_P$ trong phương trình 1.

$$V_2=A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]\:\:\:\:\:Equation\:2$$

Ở đâu,

$T_P$ là thời gian lặp lại xung

Chúng tôi sẽ nhận được subtractor output bằng cách trừ Phương trình 2 khỏi Phương trình 1.

$$V_1-V_2=A\sin\left [ 2\pi f_dt-\phi_0 \right ]-A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]$$

$$\Rightarrow V_1-V_2=2A\sin\left [ \frac{ 2\pi f_dt-\phi_0-\left [ 2\pi f_d\left ( t-T_P \right )-\phi_0 \right ]}{2}\right ]\cos\left [ \frac{ 2\pi f_dt-\phi_o+2\pi f_d\left ( t-T_P \right )-\phi_0 }{2}\right ]$$

$$V_1-V_2=2A\sin\left [ \frac{2\pi f_dT_P}{2} \right ]\cos\left [ \frac{2\pi f_d\left ( 2t-T_P \right )-2\phi_0}{2} \right ]$$

$$\Rightarrow V_1-V_2=2A\sin\left [ \pi f_dT_p \right ]\cos\left [ 2\pi f_d\left ( t-\frac{T_P}{2} \right )-\phi_0 \right ]\:\:\:\:\:Equation\:3$$

Đầu ra của bộ trừ được áp dụng làm đầu vào cho Bộ chỉnh lưu toàn sóng. Do đó, đầu ra của Full Wave Rectifier có dạng như trong hình sau. Nó không là gì ngoàifrequency response của bộ hủy dòng trễ duy nhất.

Từ phương trình 3, chúng ta có thể quan sát thấy rằng đáp ứng tần số của bộ hủy dòng trễ đơn trở thành 0, khi $\pi f_dT_P$ bằng integer multiples of $\pi$ Điều này có nghĩa là, $\pi f_dT_P$ bằng $n\pi$ Về mặt toán học, nó có thể được viết là

$$\pi f_dT_P=n\pi$$

$$\Rightarrow f_dT_P=n$$

$$\Rightarrow f_d=\frac{n}{T_P}\:\:\:\:\:Equation\:4$$

Từ phương trình 4, chúng ta có thể kết luận rằng đáp ứng tần số của bộ hủy dòng trễ đơn trở thành 0, khi tần số Doppler $f_d$ bằng bội số nguyên của nghịch đảo của thời gian lặp lại xung $T_P$.

Chúng ta biết mối quan hệ sau đây giữa thời gian lặp lại xung và tần số lặp lại xung.

$$f_d=\frac{1}{T_P}$$

$$\Rightarrow \frac{1}{T_P}=f_P\:\:\:\:\:Equation\:5$$

Chúng ta sẽ nhận được phương trình sau đây, bằng cách thay thế phương trình 5 vào phương trình 4.

$$\Rightarrow f_d=nf_P\:\:\:\:\:Equation\:6$$

Từ phương trình 6, chúng ta có thể kết luận rằng đáp ứng tần số của bộ hủy dòng trễ đơn trở thành 0, khi tần số Doppler, $f_d$ bằng bội số nguyên của tần số lặp lại xung $f_P$.

Tốc độ mù mịt

Từ những gì chúng tôi đã học được cho đến nay, bộ hủy dòng trễ duy nhất loại bỏ các thành phần DC của tín hiệu tiếng vọng nhận được từ các mục tiêu tĩnh, khi $n$bằng không. Ngoài ra, nó cũng loại bỏ các thành phần AC của tín hiệu tiếng vọng nhận được từ các mục tiêu không đứng yên, khi tần số Doppler$f_d$ bằng số nguyên (other than zero) bội số của tần số lặp lại xung $f_P$.

Vì vậy, các vận tốc tương đối mà tại đó đáp ứng tần số của bộ hủy dòng trễ đơn trở thành 0 được gọi là blind speeds. Về mặt toán học, chúng ta có thể viết biểu thức cho tốc độ mù$v_n$ như -

$$v_n=\frac{n\lambda}{2T_P}\:\:\:\:\:Equation\:7$$

$$\Rightarrow v_n=\frac{n\lambda f_P}{2}\:\:\:\:\:Equation\:8$$

Ở đâu,

$n$ là một số nguyên và nó bằng 1, 2, 3, v.v.

$\lambda$ là bước sóng hoạt động

Vấn đề ví dụ

Radar MTI hoạt động ở tần số $6GHZ$ với tần số lặp lại xung là $1KHZ$. Tìm thứ nhất, thứ hai và thứ bablind speeds của Radar này.

Giải pháp

Được,

Tần số hoạt động của MTI Radar, $f=6GHZ$

Tần số lặp lại xung, $f_P=1KHZ$.

Sau đây là công thức cho operating wavelength $\lambda$ về tần số hoạt động, f.

$$\lambda=\frac{C}{f}$$

Thay thế, $C=3\times10^8m/sec$ và $f=6GHZ$ trong phương trình trên.

$$\lambda=\frac{3\times10^8}{6\times10^9}$$

$$\Rightarrow \lambda=0.05m$$

Nên operating wavelength $\lambda$ bằng $0.05m$, khi tần số hoạt động f là $6GHZ$.

Chúng tôi biết những điều sau đây formula for blind speed.

$$v_n=\frac{n\lambda f_p}{2}$$

Bằng cách thay thế, $n$= 1,2 & 3 trong phương trình trên, chúng ta sẽ nhận được các phương trình sau cho tốc độ mù thứ nhất, thứ hai và thứ ba tương ứng.

$$v_1=\frac{1\times \lambda f_p}{2}=\frac{\lambda f_p}{2}$$

$$v_2=\frac{2\times \lambda f_p}{2}=2\left ( \frac{\lambda f_p}{2} \right )=2v_1$$

$$v_3=\frac{3\times \lambda f_p}{2}=3\left ( \frac{\lambda f_p}{2} \right )=3v_1$$

Substitute giá trị của $\lambda$ và $f_P$ trong phương trình tốc độ mù đầu tiên.

$$v_1=\frac{0.05\times 10^3}{2}$$

$$\Rightarrow v_1=25m/sec$$

Do đó, first blind speed $v_1$ bằng $25m/sec$ cho các thông số kỹ thuật nhất định.

Chúng tôi sẽ nhận được các giá trị của second & third blind speeds như $50m/sec$& $75m/sec$ tương ứng bằng cách thay giá trị của ð ?? '£ 1 vào phương trình tốc độ mù thứ hai và thứ ba.

Bộ hủy dòng trễ kép

Chúng tôi biết rằng một bộ hủy dòng trễ bao gồm một dòng trễ và một bộ trừ. Nếu hai bộ hủy dòng trễ như vậy được xếp tầng với nhau, thì sự kết hợp đó được gọi là bộ hủy dòng trễ kép. Cácblock diagram của bộ hủy dòng trễ kép được hiển thị trong hình sau.

Để cho $p\left ( t \right )$ và $q\left ( t \right )$là đầu vào và đầu ra của bộ hủy dòng trễ đầu tiên. Chúng ta sẽ nhận được quan hệ toán học sau đây từfirst delay line canceller.

$$q\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )\:\:\:\:\:Equation\:9$$

Đầu ra của bộ hủy dòng trễ đầu tiên được áp dụng làm đầu vào cho bộ hủy dòng trễ thứ hai. Vì thế,$q\left ( t \right )$sẽ là đầu vào của bộ hủy dòng trễ thứ hai. Để cho$r\left ( t \right )$là đầu ra của bộ hủy dòng trễ thứ hai. Chúng ta sẽ nhận được quan hệ toán học sau đây từsecond delay line canceller.

$$r\left ( t \right )=q\left ( t \right )-q\left ( t-T_P \right )\:\:\:\:\:Equation\:10$$

Thay thế $t$ bởi $t-T_P$ trong phương trình 9.

$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-T_P-T_P \right )$$

$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-2T_P \right )\:\:\:\:\:Equation\:11$$

Substitute, Phương trình 9 và Phương trình 11 trong Phương trình 10.

$$r\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )-\left [ p\left ( t-T_P \right )-p\left ( t-2T_P \right ) \right ]$$

$$\Rightarrow r\left ( t \right )=p\left ( t \right )-2p\left ( t-T_P \right )+p\left ( t-2T_P \right )\:\:\:\:\:Equation\:12$$

Các advantagecủa bộ hủy dòng trễ kép là nó từ chối sự lộn xộn một cách rộng rãi. Đầu ra của hai bộ hủy dòng trễ, được xếp tầng, sẽ bằng bình phương đầu ra của bộ hủy dòng trễ đơn.

Vì vậy, độ lớn của đầu ra của bộ hủy dòng trễ kép, có mặt ở máy thu Radar MTI sẽ bằng $4A^2\left ( \sin\left [ \pi f_dT_P \right ] \right )^2$.

Đặc tính đáp ứng tần số của cả bộ hủy dòng trễ kép và sự kết hợp phân tầng của hai bộ hủy dòng trễ là giống nhau. Cácadvantage của bộ hủy dòng trễ miền thời gian là nó có thể hoạt động cho tất cả các dải tần số.

Hệ thống Radar - Theo dõi Radar

Radar, được sử dụng để theo dõi đường đi của một hoặc nhiều mục tiêu, được gọi là Tracking Radar. Nói chung, nó thực hiện các chức năng sau trước khi bắt đầu hoạt động theo dõi.

• Phát hiện mục tiêu
• Phạm vi của mục tiêu
• Tìm độ cao và góc phương vị
• Tìm dịch chuyển tần số Doppler

Vì vậy, theo dõi Radar theo dõi mục tiêu bằng cách theo dõi một trong ba thông số - phạm vi, góc, dịch chuyển tần số Doppler. Hầu hết các Radar theo dõi sử dụngprinciple of tracking in angle. Bây giờ, chúng ta hãy thảo luận về theo dõi góc là gì.

Theo dõi góc

Các chùm bút chì của Radar Antenna thực hiện theo dõi theo góc. Trục của Radar Antenna được coi là hướng tham chiếu. Nếu hướng của mục tiêu và hướng tham chiếu không giống nhau, thì sẽ cóangular error, không là gì ngoài sự khác biệt giữa hai hướng.

Nếu tín hiệu lỗi góc được áp dụng cho hệ thống điều khiển servo, thì nó sẽ di chuyển trục của Ăng-ten Radar về hướng mục tiêu. Cả trục của Ăng ten Radar và hướng của mục tiêu sẽcoincidekhi sai số góc bằng không. Tồn tại một cơ chế phản hồi trong Radar theo dõi, cơ chế này hoạt động cho đến khi lỗi góc trở thành 0.

Sau đây là two techniques, được sử dụng trong theo dõi góc.

• Lobing tuần tự
• Quét hình nón

Bây giờ, chúng ta hãy thảo luận về hai kỹ thuật này từng cái một.

Lobing tuần tự

Nếu các chùm Antenna được chuyển đổi luân phiên giữa hai mẫu để theo dõi mục tiêu, thì nó được gọi là sequential lobing. Nó còn được gọi là chuyển mạch tuần tự và chuyển mạch thùy. Kỹ thuật này được sử dụng để tìm lỗi góc trong một tọa độ. Nó cung cấp các chi tiết về cả độ lớn và hướng của sai số góc.

Hình sau cho thấy một ví dụ về đăng nhập tuần tự polar coordinates.

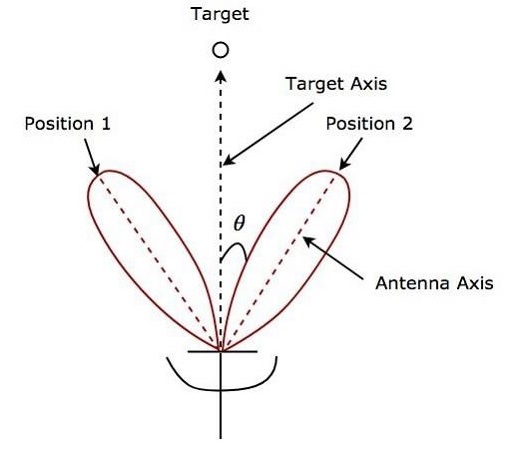
Như trong hình, các tia Ăng-ten chuyển đổi luân phiên giữa Vị trí 1 và Vị trí 2. Lỗi góc θ được chỉ ra trong hình trên. Lobing tuần tự cung cấp vị trí của mục tiêu với độ chính xác cao. Đây là chínhadvantage của phân đoạn tuần tự.

Quét hình nón

Nếu chùm tia Ăng-ten liên tục quay để theo dõi mục tiêu, thì nó được gọi là conical scanning. Điều chế quét hình nón được sử dụng để tìm vị trí của mục tiêu. Hình sau cho thấy một ví dụ về quét hình nón.

Squint anglelà góc giữa trục chùm và trục quay và nó được thể hiện trong hình trên. Tín hiệu tiếng vọng thu được từ mục tiêu được điều chế ở tần số bằng tần số mà chùm Antenna quay.

Góc giữa hướng của mục tiêu và trục quay xác định amplitude of the modulated signal. Vì vậy, điều chế quét hình nón phải được trích xuất từ ​​tín hiệu tiếng vọng và sau đó nó được áp dụng cho hệ thống điều khiển servo, hệ thống này sẽ di chuyển trục chùm Antenna theo hướng của mục tiêu.

Hệ thống Radar - Tham số Antenna

An Antenna hay Aerial là bộ chuyển đổi, biến công suất điện thành sóng điện từ và ngược lại.

Một Antenna có các thông số sau:

• Directivity
• Hiệu quả khẩu độ
• Hiệu quả Antenna
• Gain

Bây giờ, chúng ta hãy thảo luận chi tiết về các thông số này -

Định hướng

Theo định nghĩa tiêu chuẩn, “Tỷ số giữa cường độ bức xạ cực đại của Ăng-ten đối tượng với cường độ bức xạ của Ăng-ten đẳng hướng hoặc tham chiếu, phát ra cùng một công suất tổng được gọi là Directivity. ”

Mặc dù Ăng-ten phát ra năng lượng, nhưng hướng mà nó phát ra có ý nghĩa quan trọng. Ăng-ten đang được nghiên cứu được gọi làsubject Antenna. Cường độ bức xạ của nó được tập trung theo một hướng cụ thể, trong khi nó đang truyền hoặc nhận. Do đó, Antenna được cho là có khả năng định hướng theo hướng cụ thể đó.

• Tỷ số giữa cường độ bức xạ theo một hướng nhất định từ Ăng-ten và cường độ bức xạ trung bình trên tất cả các hướng, được gọi là Directivity.

• Nếu hướng cụ thể đó không được chỉ định, thì hướng mà cường độ tối đa được quan sát, có thể được coi là hướng của Antenna đó.

• Định hướng của một Antenna không đẳng hướng bằng tỷ số giữa cường độ bức xạ theo phương cho trước với cường độ bức xạ của nguồn đẳng hướng.

Mathematically, chúng ta có thể viết biểu thức cho Directivity dưới dạng:

$$Directivity=\frac{U_{Max}\left (\theta,\phi\right )}{U_0}$$

Ở đâu,

$U_{Max}\left (\theta,\phi\right )$ là cường độ bức xạ tối đa của Antenna chủ thể

$U_0$ là cường độ bức xạ của một Anten đẳng hướng.

Hiệu quả khẩu độ

Theo định nghĩa tiêu chuẩn, “Aperture efficiency của Antenna là tỷ lệ giữa vùng bức xạ hiệu quả (hoặc vùng hiệu dụng) với vùng vật lý của khẩu độ. ”

Ăng-ten bức xạ công suất thông qua một khẩu độ. Bức xạ này phải có hiệu quả với tổn thất tối thiểu. Khu vực vật lý của khẩu độ cũng cần được xem xét, vì hiệu quả của bức xạ phụ thuộc vào diện tích của khẩu độ, vật lý trên Antenna.

Mathematically, chúng ta có thể viết biểu thức cho Hiệu quả khẩu độ $\epsilon_A$ như

$$\epsilon _A=\frac{A_{eff}}{A_p}$$

Ở đâu,

$A_{eff}$ là khu vực hiệu quả

$A_P$ là khu vực vật lý

Hiệu quả Antenna

Theo định nghĩa tiêu chuẩn, “Antenna Efficiency là tỷ số giữa công suất bức xạ của Anten với công suất đầu vào được Anten chấp nhận ”.

Bất kỳ Ăng-ten nào được thiết kế để phát ra công suất với tổn hao tối thiểu cho một đầu vào nhất định. Hiệu quả của một Antenna giải thích mức độ một Antenna có thể cung cấp hiệu quả đầu ra của nó với tổn thất tối thiểu trong đường truyền. Nó còn được gọi làRadiation Efficiency Factor của Antenna.

Mathematically, chúng ta có thể viết biểu thức cho hiệu suất của ăng-ten 𝜂𝑒 dưới dạng:

$$\eta _e=\frac{P_{Rad}}{P_{in}}$$

Ở đâu,

$P_{Rad}$ là lượng điện tỏa ra

$P_{in}$ là nguồn đầu vào cho Ăng-ten

Thu được

Theo định nghĩa tiêu chuẩn, “Gain của một Ăng-ten là tỷ số giữa cường độ bức xạ theo một hướng nhất định với cường độ bức xạ thu được nếu công suất mà Ăng-ten chấp nhận được bức xạ đẳng hướng ”.

Đơn giản, Gaincủa một Ăng-ten có tính đến Hướng của Ăng-ten cùng với hiệu suất hiệu quả của nó. Nếu công suất được chấp nhận bởi Ăng-ten được bức xạ đẳng hướng (có nghĩa là theo mọi hướng), thì cường độ bức xạ mà chúng ta nhận được có thể được lấy làm tham chiếu.

• Thời hạn Antenna gain mô tả mức công suất được truyền theo hướng của bức xạ đỉnh tới công suất của một nguồn đẳng hướng.

• Độ lợi thường được đo bằng dB.

• Không giống như Directivity, Antenna gain cũng tính đến những mất mát xảy ra và do đó tập trung vào hiệu quả.

Mathematically, chúng ta có thể viết biểu thức cho Antenna Gain $G$ như -

$$G=\eta_eD$$

Ở đâu,

$\eta_e$ là hiệu suất của Antenna

$D$ là Hướng của Ăng-ten

Hệ thống radar - Anten rađa

Trong chương này, chúng ta hãy tìm hiểu về Anten, rất hữu ích trong giao tiếp bằng Radar. Chúng ta có thể phân loại Anten Radar thành các loại sautwo types dựa trên cấu trúc vật lý.

• Ăng ten phản xạ hình parabol
• Ăng ten ống kính

Trong các phần tiếp theo của chúng tôi, chúng tôi sẽ thảo luận chi tiết về hai loại Anten.

Ăng ten phản xạ hình parabol

Anten phản xạ Parabol là Anten vi sóng. Kiến thức về bộ phản xạ parabol là điều cần thiết để hiểu sâu hơn về hoạt động của ăng-ten.

Nguyên lý hoạt động

Parabola không là gì khác ngoài Locus của các điểm, di chuyển theo cách mà khoảng cách của nó từ điểm cố định (được gọi là tiêu điểm) cộng với khoảng cách của nó từ một đường thẳng (được gọi là directrix) là không đổi.

Hình sau cho thấy geometry of parabolic reflector. Các điểm F và V lần lượt là tiêu điểm (nguồn cấp dữ liệu) và đỉnh. Đường nối F và V là trục đối xứng.$P_1Q_1, P_2Q_2$ và $P_3Q_3$là các tia phản xạ. Đường thẳng L đại diện cho ma trận trực tiếp mà các điểm phản xạ nằm trên đó (có nghĩa là chúng đang thẳng hàng).

Như thể hiện trong hình, khoảng cách giữa F và L là không đổi đối với sóng được tiêu điểm. Sóng phản xạ tạo thành mặt trước sóng chuẩn trực, nằm ngoài hình parabol. Tỷ lệ độ dài tiêu cự trên kích thước khẩu độ (tức là$f/D$ ) được gọi là “f over D ratio”. Đây là một tham số quan trọng của phản xạ parabol và giá trị của nó thay đổi từ0.25 to 0.50.

Các law of reflectionnói rằng góc tới và góc phản xạ bằng nhau. Định luật này khi được sử dụng cùng với một parabol sẽ giúp chùm sáng tập trung. Hình dạng của parabol khi được sử dụng cho mục đích phản xạ sóng, thể hiện một số đặc tính của parabol, giúp ích cho việc xây dựng Antenna, sử dụng sóng phản xạ.

Thuộc tính của Parabol

Sau đây là các thuộc tính khác nhau của Parabol:

• Tất cả các sóng xuất phát từ tiêu điểm phản xạ trở lại trục parabol. Do đó, tất cả các sóng tới khẩu độ đều cùng pha.

• Khi các sóng cùng pha, chùm bức xạ dọc theo trục parabol sẽ mạnh và tập trung.

Theo những điểm này, các gương phản xạ hình parabol giúp tạo ra khả năng định hướng cao với độ rộng chùm tia hẹp hơn.

Cấu tạo & Hoạt động của một Bộ phản xạ Parabol

Nếu một Anten phản xạ Parabol được sử dụng cho transmitting a signal, tín hiệu từ nguồn cấp phát ra từ Ăng ten lưỡng cực hoặc Ăng ten sừng, để tập trung sóng vào parabol. Có nghĩa là, các sóng đi ra khỏi tiêu điểm và đập vào mặt phản xạ hình parabol. Sóng này bây giờ được phản xạ dưới dạng sóng chuẩn trực, như đã thảo luận trước đây, để được truyền đi.

Antenna tương tự được sử dụng như một receiver. Khi sóng điện từ chạm vào hình parabol, sóng sẽ bị phản xạ vào điểm truyền. Ăng-ten lưỡng cực hay Ăng-ten sừng, đóng vai trò là Ăng-ten thu tại nguồn cấp của nó nhận tín hiệu này, để chuyển đổi tín hiệu này thành tín hiệu điện và chuyển tiếp đến mạch thu.

Độ lợi của paraboloid là một hàm của tỷ lệ khẩu độ $D/\lambda$. Công suất bức xạ hiệu quả(ERP) của một Ăng-ten là phép nhân của công suất đầu vào được cấp cho Ăng-ten và công suất của nó.

Thông thường Ăng-ten sừng dẫn sóng được sử dụng làm bộ tản nhiệt cấp cho Ăng-ten phản xạ hình parabol. Cùng với kỹ thuật này, chúng tôi có hai loại nguồn cấp dữ liệu sau được cung cấp cho Antenna phản xạ hình parabol.

• Cassegrain Feed
• Gregorian Feed

Cassegrain Feed

Trong loại này, nguồn cấp dữ liệu nằm ở đỉnh của paraboloid, không giống như trong gương phản xạ parabol. Một tấm phản xạ hình lồi, hoạt động như một hypeboloid được đặt đối diện với nguồn cấp của Ăng-ten. Nó còn được gọi làsecondary hyperboloid reflectorhoặc phản xạ phụ. Nó được đặt theo cách sao cho một trong các tiêu điểm của nó trùng với trọng tâm của paraboloid. Do đó, sóng bị phản xạ hai lần.

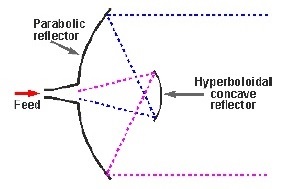
Hình trên mô tả mô hình làm việc của thức ăn chăn nuôi bằng hạt cải.

Gregorian Feed

Loại nguồn cấp dữ liệu có một cặp cấu hình nhất định và ở đó chiều rộng chùm tia cấp dữ liệu được tăng dần trong khi kích thước Antenna được giữ cố định được gọi là Gregorian feed. Ở đây, hyperboloid hình lồi của Cassegrain được thay thế bằng một mặt phản xạ paraboloid hình lõm, tất nhiên, có kích thước nhỏ hơn.

Các bộ phản xạ kiểu nguồn cấp dữ liệu Gregorian này có thể được sử dụng theo bốn cách sau:

• Hệ thống Gregorian sử dụng gương phản xạ phụ hình elip ở điểm F1.

• Hệ thống Gregorian sử dụng gương phản xạ phụ hình elip ở điểm F2.

• Hệ thống Cassegrain sử dụng gương phản xạ phụ hyperboloid (lồi).

• Hệ thống Cassegrain sử dụng gương phản xạ phụ hyperboloid (lõm nhưng nguồn cấp dữ liệu ở rất gần nó).

Trong số các loại Anten phản xạ khác nhau, các loại phản xạ parabol đơn giản và phản xạ parabol nguồn cấp dữ liệu Cassegrain là những loại được sử dụng phổ biến nhất.

Ăng ten ống kính

Anten ống kính sử dụng bề mặt cong để truyền và nhận tín hiệu. Các ăng-ten này được tạo thành từ thủy tinh, nơi tuân theo các đặc tính hội tụ và phân kỳ của thấu kính. Cácfrequency range việc sử dụng Ăng-ten ống kính bắt đầu từ 1 GHz nhưng việc sử dụng nó lớn hơn ở 3 GHz and above.

Cần có kiến ​​thức về Ống kính để hiểu sâu về hoạt động của Ăng-ten ống kính. Nhớ lại rằng một thấu kính thủy tinh bình thường hoạt động trênprinciple of refraction.

Cấu tạo & Hoạt động của Ăng-ten ống kính

Nếu một nguồn sáng được cho là có mặt tại tiêu điểm của thấu kính, ở tiêu điểm cách thấu kính, thì các tia đi qua thấu kính là chuẩn trực hoặc parallel rays trên mặt trận sóng máy bay.

Có hai hiện tượng xảy ra khi tia rơi từ các mặt khác nhau của thấu kính. Chúng được đưa ra ở đây -

• Tia đi qua tâm Thấu kính bị khúc xạ nhỏ hơn tia đi qua các mép của Thấu kính. Tất cả các tia được gửi song song với mặt trước sóng phẳng. Hiện tượng này của thấu kính được gọi làDivergence.

• Quy trình tương tự sẽ bị đảo ngược nếu một chùm ánh sáng được gửi từ bên phải sang bên trái của cùng một Thấu kính. Khi đó chùm tia khúc xạ và gặp nhau tại một điểm gọi là tiêu điểm, cách thấu kính một khoảng tiêu cự. Hiện tượng này được gọi làConvergence.

Sơ đồ sau sẽ giúp chúng ta hiểu rõ hơn về hiện tượng.

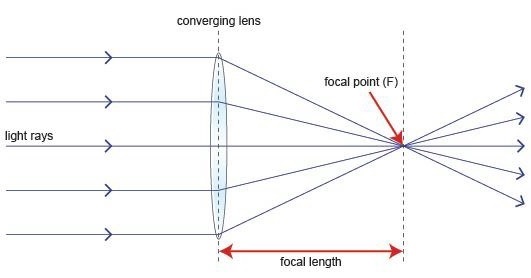
Các ray diagrambiểu diễn tiêu điểm và tiêu cự từ nguồn đến Thấu kính. Tia song song thu được còn gọi là tia chuẩn trực.

Trong hình trên, nguồn tại tiêu điểm, cách thấu kính một khoảng tiêu cự là chuẩn trực trong mặt trước sóng phẳng. Hiện tượng này có thể bị đảo ngược, có nghĩa là ánh sáng nếu được gửi từ phía bên trái sẽ được hội tụ ở phía bên phải của Ống kính.

Đó là vì điều này reciprocity, Ống kính có thể được sử dụng như một Ăng-ten, vì hiện tượng tương tự giúp sử dụng cùng một Ăng-ten cho cả truyền và nhận.

Để đạt được đặc tính hội tụ ở tần số cao hơn, chiết suất phải nhỏ hơn sự thống nhất. Dù có thể là chỉ số khúc xạ, mục đích của Thấu kính là làm thẳng dạng sóng. Dựa trên điều này, Ống kính mặt phẳng E và Ống kính mặt phẳng H được phát triển, chúng cũng làm chậm hoặc tăng tốc độ đầu sóng.

Hệ thống radar - Bộ thu lọc phù hợp

Nếu một bộ lọc tạo ra một đầu ra theo cách mà nó tối đa hóa tỷ lệ giữa công suất đỉnh đầu ra và công suất nhiễu trung bình trong đáp ứng tần số của nó, thì bộ lọc đó được gọi là Matched filter.

Đây là một tiêu chí quan trọng, được xem xét trong khi thiết kế bất kỳ máy thu Radar nào. Trong chương này, chúng ta hãy thảo luận về chức năng đáp ứng tần số của bộ lọc phù hợp và đáp ứng xung của bộ lọc phù hợp.

Chức năng đáp ứng tần số của Bộ lọc phù hợp

Đáp ứng tần số của bộ lọc Phù hợp sẽ tỷ lệ với sự liên hợp phức tạp của phổ của tín hiệu đầu vào. Về mặt toán học, chúng ta có thể viết biểu thức chofrequency response function, $H\left (f\right )$ của bộ lọc Đối sánh dưới dạng -

$$H\left (f\right )=G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:Equation\:1$$

Ở đâu,

$G_a$ là mức tăng tối đa của bộ lọc Đối sánh

$S\left (f\right )$ là biến đổi Fourier của tín hiệu đầu vào, $s\left (t\right )$

$S^\ast\left (f\right )$ là liên hợp phức tạp của $S\left (f\right )$

$t_1$ là khoảng thời gian mà tín hiệu quan sát được là tối đa

Nói chung, giá trị của $G_a$được coi là một. Chúng ta sẽ nhận được phương trình sau bằng cách thay thế$G_a=1$ trong phương trình 1.

$$H\left (f\right )=S^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:Equation\:2$$

Chức năng đáp ứng tần số, $H\left (f\right )$ của bộ lọc Đối sánh đang có magnitude của $S^\ast\left (f\right )$ và phase angle của $e^{-j2\pi ft_1}$, thay đổi đồng đều theo tần số.

Phản hồi xung của Bộ lọc phù hợp

Trong time domain, chúng tôi sẽ nhận được đầu ra, $h(t)$ của bộ thu lọc phù hợp bằng cách áp dụng biến đổi Fourier ngược của hàm đáp ứng tần số, $H(f)$.

$$h\left (t\right )=\int_{-\infty }^{\infty }H\left (f\right )e^{-j2\pi ft_1}df\:\:\:\:\:Equation\:3$$

Substitute, Phương trình 1 trong Phương trình 3.

$$h\left (t\right )=\int_{-\infty }^{\infty }\lbrace G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\rbrace e^{j2\pi ft}df$$

$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\ast\left (f\right )e^{-j2\pi f\left (t_1-t\right )}df\:\:\:\:\:Equation\:4$$

Chúng tôi biết mối quan hệ sau đây.

$$S^\ast\left (f\right )=S\left (-f\right )\:\:\:\:\:Equation\:5$$

Substitute, Phương trình 5 trong Phương trình 4.

$$h\left (t\right )=\int_{-\infty }^{\infty }G_aS(-f)e^{-j2\pi f\left (t_1-t\right )}df$$

$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\left (f\right )e^{j2\pi f\left (t_1-t\right )}df$$

$$\Rightarrow h\left (t\right )=G_as(t_1−t)\:\:\:\:\:Equation\:6$$

Nói chung, giá trị của $G_a$được coi là một. Chúng ta sẽ nhận được phương trình sau bằng cách thay thế$G_a=1$ trong phương trình 6.

$$h(t)=s\left (t_1-t\right )$$

Phương trình trên chứng minh rằng impulse response of Matched filter là hình ảnh phản chiếu của tín hiệu nhận được trong khoảng thời gian tức thì $t_1$. Các hình sau đây minh họa khái niệm này.

Tín hiệu nhận được, $s\left (t\right )$ và phản ứng xung động, $h\left (t\right )$ của bộ lọc phù hợp tương ứng với tín hiệu, $s\left (t\right )$ được hiển thị trong các hình trên.

Hệ thống Radar - Màn hình Radar

Một công cụ điện tử, được sử dụng để hiển thị dữ liệu một cách trực quan được gọi là màn hình. Vì vậy, công cụ điện tử hiển thị thông tin về mục tiêu của Radar một cách trực quan được gọi làRadar display. Nó hiển thị thông tin tín hiệu tiếng vọng một cách trực quan trên màn hình.

Các loại màn hình Radar

Trong phần này, chúng ta sẽ tìm hiểu về các loại Màn hình Radar khác nhau. Màn hình Radar có thể được phân loại thành các loại sau.

Phạm vi

Nó là một màn hình Radar hai chiều. Các tọa độ ngang và dọc lần lượt thể hiện phạm vi và biên độ dội âm của mục tiêu. Trong phạm vi A, điều chế độ võng diễn ra. Nó phù hợp hơn chomanually tracking Radar.

B-Phạm vi

Nó là một màn hình Radar hai chiều. Các tọa độ ngang và dọc lần lượt thể hiện góc phương vị và phạm vi của mục tiêu. Trong phạm vi B, điều chế cường độ diễn ra. Nó phù hợp hơn chomilitary Radars.

C-Phạm vi

Nó là một màn hình Radar hai chiều. Các tọa độ ngang và dọc lần lượt thể hiện góc phương vị và góc nâng. Trong phạm vi C, điều biến cường độ diễn ra.

D-Phạm vi

Nếu chùm điện tử bị lệch hướng hoặc điểm được điều biến cường độ xuất hiện trên màn hình Radar do sự hiện diện của mục tiêu, thì đó được gọi là đốm sáng. C-Scope trở thành D-Scope, khi các vỉ mở rộng theo chiều dọc để cung cấp khoảng cách.

Phạm vi điện tử

Nó là một màn hình Radar hai chiều. Các tọa độ ngang và dọc lần lượt thể hiện khoảng cách và góc nâng. Trong phạm vi E, điều biến cường độ diễn ra.

Phạm vi F

Nếu Ăng ten Radar nhắm vào mục tiêu, thì F-Scope sẽ hiển thị mục tiêu dưới dạng một đốm sáng tập trung. Vì vậy, độ dịch chuyển theo phương ngang và phương thẳng đứng của vết bay lần lượt thể hiện sai số ngắm theo phương ngang và phương thẳng đứng.

G-Phạm vi

Nếu Ăng-ten Radar được nhắm vào mục tiêu, thì G-Scope sẽ hiển thị mục tiêu dưới dạng đốm sáng tập trung theo bên. Dịch chuyển ngang và dọc của quả bóng lần lượt thể hiện sai số ngắm bắn theo phương ngang và phương thẳng đứng.

Phạm vi H

Đây là phiên bản sửa đổi của B-Scope để cung cấp thông tin về góc nâng của mục tiêu. Nó hiển thị mục tiêu dưới dạng hai vỉ, được đặt gần nhau. Điều này có thể được coi gần đúng với một đường sáng ngắn và độ dốc của đường này sẽ tỷ lệ với sin của góc nâng.

I-Phạm vi

Nếu Ăng ten Radar nhắm vào mục tiêu, thì I-Scope hiển thị mục tiêu dưới dạng circle. Bán kính của vòng tròn này sẽ tỷ lệ thuận với khoảng cách của mục tiêu. Nếu Ăng ten Radar nhắm mục tiêu không chính xác, thì I-Scope sẽ hiển thị mục tiêu dưới dạng một đoạn thay vì vòng tròn. Độ dài cung của đoạn đó sẽ tỷ lệ nghịch với độ lớn của lỗi trỏ.

J-Phạm vi

Nó là phiên bản sửa đổi của A-Scope. Nó hiển thị mục tiêu dưới dạng lệch hướng tâm so với cơ sở thời gian.

K-Phạm vi

Nó là phiên bản sửa đổi của A-Scope. Nếu Ăng-ten Radar nhắm vào mục tiêu, thì K-Scope sẽ hiển thị mục tiêu dưới dạng một cặp lệch hướng dọc, có chiều cao bằng nhau. Nếu Antenna của Radar nhắm mục tiêu không chính xác, thì sẽ xảy ra lỗi trỏ. Vì vậy, độ lớn và hướng của lỗi trỏ phụ thuộc vào sự khác biệt giữa hai độ lệch dọc.

L-Phạm vi

Nếu Ăng-ten Radar nhắm vào mục tiêu, thì L-Scope hiển thị mục tiêu dưới dạng hai bọng ngang có biên độ bằng nhau. Một đốm sáng ngang nằm ở bên phải của cơ sở thời gian dọc trung tâm và một điểm khác nằm ở bên trái của cơ sở thời gian dọc trung tâm.

Phạm vi M

Nó là phiên bản sửa đổi của A-Scope. Tín hiệu bệ có thể điều chỉnh phải được di chuyển dọc theo đường cơ sở cho đến khi nó trùng với các tín hiệu lệch hướng đến từ vị trí nằm ngang của mục tiêu. Bằng cách này, khoảng cách của mục tiêu có thể được xác định.

N-Phạm vi

Nó là phiên bản sửa đổi của K-Scope. Một tín hiệu bệ điều chỉnh được sử dụng để đo khoảng cách.

Phạm vi O

Nó là phiên bản sửa đổi của A-Scope. Chúng tôi sẽ nhận được O-Scope, bằng cách bao gồm một rãnh có thể điều chỉnh thành A-Scope để đo khoảng cách.

Phạm vi P

Nó là một màn hình Radar, sử dụng điều chế cường độ. Nó hiển thị thông tin của tín hiệu tiếng vang dưới dạng xem kế hoạch. Phạm vi và góc phương vị được hiển thị trong tọa độ cực. Do đó, nó được gọi làPlan Position Indicator hoặc là PPI display.

Phạm vi R

Nó là một màn hình Radar, sử dụng điều chế cường độ. Các tọa độ ngang và dọc đại diện cho phạm vi và độ cao của mục tiêu tương ứng. Do đó, nó được gọi làRange-Height Indicator hoặc là RHI display.

Hệ thống radar - Bộ đảo mặt

Trong giao tiếp hai chiều, nếu chúng ta phải sử dụng cùng một Antenna cho cả việc truyền và nhận tín hiệu, thì chúng ta yêu cầu Duplexer. Duplexerlà một công tắc viba, kết nối Antenna với phần phát để truyền tín hiệu. Do đó, Radar không thể nhận được tín hiệu trong thời gian truyền.

Tương tự, nó kết nối Antenna với phần đầu thu để thu tín hiệu. Radar không thể truyền tín hiệu trong thời gian nhận. Bằng cách này, Duplexer cô lập cả phần phát và phần thu.

Các loại song công

Trong phần này, chúng ta sẽ tìm hiểu về các loại bộ song công. Chúng ta có thể phân loại Duplexers thành các loại sauthree types.

• Bộ đảo mặt loại nhánh
• Bộ đảo mặt cân bằng
• Circulator as Duplexer

Trong các phần tiếp theo của chúng tôi, chúng tôi sẽ thảo luận chi tiết về các loại Duplexers.

Bộ đảo mặt loại nhánh

Bộ song công kiểu nhánh bao gồm hai công tắc - công tắc Truyền-Nhận (TR) và công tắc Chống Truyền-Nhận (ATR). Hình sau cho thấyblock diagram của Bộ đảo mặt kiểu nhánh -

Như trong hình, hai công tắc, TR & ATR được đặt ở khoảng cách $\lambda/4$ từ đường truyền và cả hai công tắc cách nhau một khoảng là $\lambda/4$. Cácworking của Bộ song công loại nhánh được đề cập bên dưới.

• Suốt trong transmission, cả TR & ATR sẽ giống như một mạch hở từ đường truyền. Do đó, Anten sẽ được kết nối với thiết bị phát thông qua đường truyền.

• Suốt trong reception, ATR sẽ giống như ngắn mạch trên đường truyền. Do đó, Antenna sẽ được kết nối với đầu thu thông qua đường truyền.

Bộ đảo mặt loại nhánh chỉ thích hợp cho các Radar giá rẻ, vì nó có ít khả năng xử lý năng lượng hơn.

Bộ đảo mặt cân bằng

Chúng tôi biết rằng một two-hole Directional Couplerlà mối nối ống dẫn sóng 4 cổng bao gồm một ống dẫn sóng chính và một ống dẫn sóng thứ cấp. Có hai lỗ nhỏ, sẽ là chung cho hai ống dẫn sóng đó.

Bộ song công cân bằng bao gồm hai ống TR. Cấu hình của Balanced Duplexer chotransmission mục đích được hiển thị trong hình sau.

Tín hiệu được tạo ra bởi máy phát phải đến được Anten để Anten truyền tín hiệu đó trong thời gian truyền. Cácsolid lines with arrow marks Hình trên thể hiện cách tín hiệu đến Antenna từ máy phát.

Các đường chấm có dấu mũi tên trong hình trên đại diện cho tín hiệu bị rò rỉ từ các ống Dual TR; điều này sẽ chỉ đạt đến tải phù hợp. Vì vậy, không có tín hiệu nào được đến máy thu.

Cấu hình của Balanced Duplexer cho reception mục đích được hiển thị trong hình dưới đây.

Chúng tôi biết rằng Antenna nhận được tín hiệu trong thời gian tiếp nhận. Tín hiệu được nhận bởi Antenna phải đến được máy thu. Cácsolid lines with arrow markstrong hình trên thể hiện cách tín hiệu đến máy thu từ Antenna. Trong trường hợp này, các ống Dual TR truyền tín hiệu từ phần đầu tiên của ống dẫn sóng đến phần tiếp theo của ống dẫn sóng.

Bộ song công cân bằng có khả năng xử lý công suất cao và băng thông lớn khi so sánh với bộ song công loại nhánh.

Circulator as Duplexer

Chúng tôi biết rằng functionality của tuần hoàn là nếu chúng ta áp dụng một đầu vào cho một cổng, thì nó sẽ được sản xuất tại cổng, nơi tiếp giáp với nó theo chiều kim đồng hồ. Không có đầu ra ở các cổng còn lại của bộ tuần hoàn.

Vì vậy, hãy xem xét một bộ tuần hoàn 4 cổng và kết nối máy phát, Antenna, máy thu và tải phù hợp với cổng1, cổng2, cổng3 và cổng4 tương ứng. Bây giờ, hãy để chúng tôi hiểu cách4-port circulator hoạt động như Duplexer.

Tín hiệu được tạo ra bởi máy phát phải đến được Ăng-ten vì Ăng-ten sẽ truyền tín hiệu đó trong transmissionthời gian. Mục đích này sẽ đạt được khi máy phát tạo ra tín hiệu tại cổng 1.

Tín hiệu được nhận bởi Antenna phải đến được máy thu trong receptionthời gian. Mục đích này sẽ đạt được khi Ăng-ten có tại cổng 2 nhận được tín hiệu bên ngoài.

Hình sau cho thấy block diagram của bộ tuần hoàn dưới dạng Duplexer -

Hình trên bao gồm một bộ tuần hoàn 4 cổng - Máy phát, Ăng-ten và tải phù hợp được kết nối tương ứng với cổng1, cổng2 và cổng 4 của bộ tuần hoàn như đã thảo luận ở đầu phần.

Bộ thu không được kết nối trực tiếp với cổng 3. Thay vào đó, các khối tương ứng với bộ giới hạn TR thụ động được đặt giữa cổng 3 của bộ tuần hoàn và bộ thu. Các khối, ống TR & bộ giới hạn Diode là các khối tương ứng với bộ giới hạn TR thụ động.

Trên thực tế, bản thân bộ tuần hoàn hoạt động như một bộ song công. Nó không yêu cầu bất kỳ khối bổ sung nào. Tuy nhiên, nó sẽ không cung cấp bất kỳ loại bảo vệ nào cho người nhận. Do đó, các khối tương ứng với bộ giới hạn TR thụ động được sử dụng để cung cấpprotection to the receiver.

Hệ thống radar - Ăng ten mảng theo giai đoạn

Một Antenna duy nhất có thể phát ra một lượng công suất nhất định theo một hướng cụ thể. Rõ ràng, lượng công suất bức xạ sẽ tăng lên khi chúng ta sử dụng nhóm Anten với nhau. Nhóm Anten được gọi làAntenna array.

Một mảng Antenna là một hệ thống bức xạ bao gồm các bộ tản nhiệt và các phần tử. Mỗi bộ tản nhiệt này có trường cảm ứng riêng. Các phần tử được đặt gần nhau đến mức mỗi phần tử nằm trong trường cảm ứng của một phần tử lân cận. Do đó, mẫu bức xạ do chúng tạo ra, sẽ làvector sum của từng cá nhân.

Các Anten bức xạ riêng lẻ và trong một mảng, bức xạ của tất cả các phần tử tổng hợp lại, tạo thành chùm bức xạ, có độ lợi cao, định hướng cao và hiệu suất tốt hơn, với tổn thất tối thiểu.

Một mảng Antenna được cho là Phased Antenna array nếu hình dạng và hướng của mẫu bức xạ phụ thuộc vào các pha và biên độ tương đối của các dòng điện có mặt tại mỗi Anten của mảng đó.

Mô hình bức xạ

Chúng ta hãy xem xét 'n' các phần tử bức xạ đẳng hướng, khi kết hợp với nhau sẽ tạo thành array. Hình dưới đây sẽ giúp bạn hiểu như vậy. Gọi khoảng cách giữa các phần tử liên tiếp là đơn vị 'd'.

Như trong hình, tất cả các phần tử bức xạ đều nhận được cùng một tín hiệu tới. Vì vậy, mỗi phần tử tạo ra một điện áp đầu ra bằng nhau là$sin \left ( \omega t \right)$. Tuy nhiên, sẽ có mộtphase difference $\Psi$giữa các phần tử kế tiếp nhau. Về mặt toán học, nó có thể được viết là -

$$\Psi=\frac{2\pi d\sin\theta }{\lambda }\:\:\:\:\:Equation\:1$$

Ở đâu,

$\theta$ là góc mà tại đó tín hiệu tới là tới trên mỗi phần tử bức xạ.

Về mặt toán học, chúng ta có thể viết các biểu thức cho output voltages các nguyên tố bức xạ 'n' riêng lẻ như

$$E_1=\sin\left [ \omega t \right]$$

$$E_2=\sin\left [\omega t+\Psi\right]$$

$$E_3=\sin\left [\omega t+2\Psi\right]$$

$$.$$

$$.$$

$$.$$

$$E_n=\sin\left [\omega t+\left (N-1\right )\Psi\right]$$

Ở đâu,

$E_1, E_2, E_3, …, E_n$lần lượt là điện áp ra của phần tử bức xạ ^thứ nhất, thứ hai, thứ ba,…, ^thứ n .

$\omega$ là tần số góc của tín hiệu.

Chúng tôi sẽ nhận được overall output voltage $E_a$của mảng bằng cách thêm điện áp đầu ra của từng phần tử có trong mảng đó, vì tất cả các phần tử bức xạ đó được kết nối trong mảng tuyến tính. Về mặt toán học, nó có thể được biểu diễn dưới dạng:

$$E_a=E_1+E_2+E_3+ …+E_n \:\:\:Equation\:2$$

Substitute, các giá trị của $E_1, E_2, E_3, …, E_n$ trong phương trình 2.

$$E_a=\sin\left [ \omega t \right]+\sin\left [\omega t+\Psi\right ]+\sin\left [\omega t+2\Psi\right ]+\sin\left [\omega t+\left (n-1\right )\Psi\right]$$

$$\Rightarrow E_a=\sin\left [\omega t+\frac{(n-1)\Psi)}{2}\right ]\frac{\sin\left [\frac{n\Psi}{2}\right]}{\sin\left [\frac{\Psi}{2}\right ]}\:\:\:\:\:Equation\:3$$

Trong phương trình 3, có hai số hạng. Từ số hạng đầu tiên, chúng ta có thể quan sát thấy rằng điện áp đầu ra tổng thể$E_a$ là một sóng hình sin có tần số góc $\omega$. Nhưng, nó đang có một sự chuyển đổi giai đoạn$\left (n−1\right )\Psi/2$. Số hạng thứ hai của phương trình 3 là mộtamplitude factor.

Độ lớn của phương trình 3 sẽ là

$$\left | E_a \right|=\left | \frac{\sin\left [\frac{n\Psi}{2}\right ]}{\sin\left [\frac{\Psi}{2}\right]} \right |\:\:\:\:\:Equation\:4$$

Chúng ta sẽ nhận được phương trình sau bằng cách thay phương trình 1 vào phương trình 4.

$$\left | E_a \right|=\left | \frac{\sin\left [\frac{n\pi d\sin\theta}{\lambda}\right]}{\sin\left [\frac{\pi d\sin\theta}{\lambda}\right ]} \right |\:\:\:\:\:Equation\:5$$

Phương trình 5 được gọi là field intensity pattern. Mẫu cường độ trường sẽ có các giá trị là số không khi tử số của phương trình 5 bằng 0

$$\sin\left [\frac{n\pi d\sin\theta}{\lambda}\right ]=0$$

$$\Rightarrow \frac{n\pi d\sin\theta}{\lambda}=\pm m\pi$$

$$\Rightarrow nd\sin\theta=\pm m\lambda$$

$$\Rightarrow \sin\theta=\pm \frac{m\lambda}{nd}$$

Ở đâu,

$m$ là một số nguyên và nó bằng 1, 2, 3, v.v.

Chúng tôi có thể tìm thấy maximum valuescủa mẫu cường độ trường bằng cách sử dụng quy tắc L-Hospital khi cả tử số và mẫu số của Phương trình 5 đều bằng không. Chúng ta có thể quan sát rằng nếu mẫu số của phương trình 5 trở thành 0, thì tử số của phương trình 5 cũng trở thành 0.

Bây giờ, chúng ta hãy lấy điều kiện để mẫu số của phương trình 5 trở thành không.

$$\sin\left [\frac{\pi d\sin\theta}{\lambda}\right ]=0$$

$$\Rightarrow \frac{\pi d\sin\theta}{\lambda}=\pm p\pi$$

$$\Rightarrow d\sin\theta=\pm p\lambda$$

$$\Rightarrow \sin\theta=\pm \frac{p\lambda}{d}$$

Ở đâu,

$p$ là một số nguyên và nó bằng 0, 1, 2, 3, v.v.

Nếu chúng ta xem xét $p$ bằng 0, thì chúng ta sẽ nhận được giá trị của $\sin\theta$bằng không. Đối với trường hợp này, chúng ta sẽ nhận được giá trị lớn nhất của mẫu cường độ trường tương ứng vớimain lobe. Chúng ta sẽ nhận được các giá trị lớn nhất của mẫu cường độ trường tương ứng vớiside lobes, khi chúng tôi xem xét các giá trị khác của $p$.

Hướng của mẫu bức xạ của mảng theo từng giai đoạn có thể được điều khiển bằng cách thay đổi các pha tương đối của dòng điện hiện tại tại mỗi Anten. Đây làadvantage của mảng quét điện tử theo từng giai đoạn.