Klassifizierungsalgorithmen - Entscheidungsbaum

Einführung in den Entscheidungsbaum

Im Allgemeinen ist die Entscheidungsbaumanalyse ein Vorhersagemodellierungswerkzeug, das in vielen Bereichen angewendet werden kann. Entscheidungsbäume können durch einen algorithmischen Ansatz erstellt werden, der den Datensatz basierend auf verschiedenen Bedingungen auf unterschiedliche Weise aufteilen kann. Entscheidungen sind die leistungsstärksten Algorithmen, die unter die Kategorie der überwachten Algorithmen fallen.

Sie können sowohl für Klassifizierungs- als auch für Regressionsaufgaben verwendet werden. Die beiden Hauptentitäten eines Baums sind Entscheidungsknoten, bei denen die Daten aufgeteilt werden und die Daten verlassen werden. Das Beispiel eines Binärbaums zur Vorhersage, ob eine Person fit oder nicht fit ist und verschiedene Informationen wie Alter, Essgewohnheiten und Bewegungsgewohnheiten liefert, ist unten angegeben.

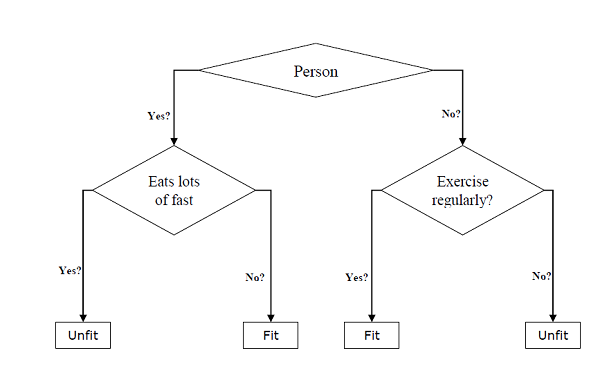
Im obigen Entscheidungsbaum sind die Fragen Entscheidungsknoten und die Endergebnisse sind Blätter. Wir haben die folgenden zwei Arten von Entscheidungsbäumen:

Classification decision trees- Bei dieser Art von Entscheidungsbäumen ist die Entscheidungsvariable kategorisch. Der obige Entscheidungsbaum ist ein Beispiel für einen Klassifizierungsentscheidungsbaum.
Regression decision trees - Bei dieser Art von Entscheidungsbäumen ist die Entscheidungsvariable kontinuierlich.

Implementieren des Entscheidungsbaumalgorithmus

Gini Index

Dies ist der Name der Kostenfunktion, mit der die binären Teilungen im Datensatz ausgewertet werden und die mit der kategorialen Zielvariablen „Erfolg“ oder „Fehler“ zusammenarbeitet.

Je höher der Wert des Gini-Index ist, desto höher ist die Homogenität. Ein perfekter Gini-Indexwert ist 0 und der schlechteste ist 0,5 (für 2-Klassen-Probleme). Der Gini-Index für einen Split kann mithilfe der folgenden Schritte berechnet werden:

Berechnen Sie zunächst den Gini-Index für Unterknoten mit der Formel p ^ 2 + q ^ 2, die die Summe des Wahrscheinlichkeitsquadrats für Erfolg und Misserfolg darstellt.
Berechnen Sie als Nächstes den Gini-Index für die Aufteilung unter Verwendung der gewichteten Gini-Bewertung jedes Knotens dieser Aufteilung.

Der CART-Algorithmus (Classification and Regression Tree) verwendet die Gini-Methode, um binäre Teilungen zu generieren.

Geteilte Schöpfung

Ein Split enthält im Wesentlichen ein Attribut im Dataset und einen Wert. Mit Hilfe der folgenden drei Teile können wir eine Aufteilung des Datensatzes erstellen:

Part1: Calculating Gini Score - Wir haben diesen Teil gerade im vorherigen Abschnitt besprochen.
Part2: Splitting a dataset- Es kann so definiert werden, dass ein Datensatz in zwei Zeilenlisten mit dem Index eines Attributs und einem geteilten Wert dieses Attributs unterteilt wird. Nachdem wir die beiden Gruppen - rechts und links - aus dem Datensatz erhalten haben, können wir den Wert der Aufteilung mithilfe des im ersten Teil berechneten Gini-Scores berechnen. Der geteilte Wert entscheidet, in welcher Gruppe sich das Attribut befindet.
Part3: Evaluating all splits- Der nächste Teil nach dem Finden des Gini-Scores und dem Aufteilen des Datensatzes ist die Bewertung aller Aufteilungen. Zu diesem Zweck müssen wir zunächst jeden Wert überprüfen, der jedem Attribut als Kandidatensplit zugeordnet ist. Dann müssen wir die bestmögliche Aufteilung finden, indem wir die Kosten der Aufteilung bewerten. Die beste Aufteilung wird als Knoten im Entscheidungsbaum verwendet.

Einen Baum bauen

Wie wir wissen, hat ein Baum Wurzelknoten und Endknoten. Nach dem Erstellen des Stammknotens können wir den Baum erstellen, indem wir zwei Teilen folgen:

Teil 1: Erstellung des Terminalknotens

Beim Erstellen von Endknoten des Entscheidungsbaums ist es wichtig zu entscheiden, wann das Wachstum des Baums beendet oder weitere Endknoten erstellt werden sollen. Dies kann unter Verwendung von zwei Kriterien erfolgen, nämlich maximaler Baumtiefe und minimaler Knotendatensätze wie folgt:

Maximum Tree Depth- Wie der Name schon sagt, ist dies die maximale Anzahl der Knoten in einem Baum nach dem Wurzelknoten. Wir müssen aufhören, Endknoten hinzuzufügen, sobald ein Baum die maximale Tiefe erreicht hat, dh sobald ein Baum die maximale Anzahl von Endknoten erreicht hat.
Minimum Node Records- Es kann als die Mindestanzahl von Trainingsmustern definiert werden, für die ein bestimmter Knoten verantwortlich ist. Wir müssen aufhören, Endknoten hinzuzufügen, sobald der Baum diese Mindestknotendatensätze erreicht hat oder unter diesem Mindestwert liegt.

Der Endknoten wird verwendet, um eine endgültige Vorhersage zu treffen.

Teil 2: Rekursive Aufteilung

Da wir verstanden haben, wann Endknoten erstellt werden müssen, können wir jetzt mit dem Erstellen unseres Baums beginnen. Rekursives Teilen ist eine Methode zum Erstellen des Baums. Bei dieser Methode können wir nach dem Erstellen eines Knotens die untergeordneten Knoten (Knoten, die einem vorhandenen Knoten hinzugefügt wurden) rekursiv für jede Datengruppe erstellen, die durch Aufteilen des Datasets generiert wird, indem dieselbe Funktion immer wieder aufgerufen wird.

Prognose

Nachdem wir einen Entscheidungsbaum erstellt haben, müssen wir eine Vorhersage darüber machen. Grundsätzlich beinhaltet die Vorhersage das Navigieren im Entscheidungsbaum mit der speziell bereitgestellten Datenzeile.

Wir können eine Vorhersage mit Hilfe der rekursiven Funktion machen, wie oben beschrieben. Dieselbe Vorhersageroutine wird erneut mit dem linken oder dem untergeordneten rechten Knoten aufgerufen.

Annahmen

Im Folgenden sind einige der Annahmen aufgeführt, die wir beim Erstellen des Entscheidungsbaums treffen:

Während der Vorbereitung von Entscheidungsbäumen dient der Trainingssatz als Wurzelknoten.
Der Entscheidungsbaumklassifizierer bevorzugt, dass die Merkmalswerte kategorisch sind. Wenn Sie fortlaufende Werte verwenden möchten, müssen diese vor der Modellbildung diskretisiert werden.
Basierend auf den Werten des Attributs werden die Datensätze rekursiv verteilt.
Der statistische Ansatz wird verwendet, um Attribute an einer beliebigen Knotenposition zu platzieren, z. B. einem Wurzelknoten oder einem internen Knoten.

Implementierung in Python

Beispiel

Im folgenden Beispiel implementieren wir den Decision Tree-Klassifikator für Pima Indian Diabetes -

Beginnen Sie zunächst mit dem Importieren der erforderlichen Python-Pakete.

import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split

Laden Sie als Nächstes den Iris-Datensatz wie folgt von seinem Weblink herunter:

col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
pima = pd.read_csv(r"C:\pima-indians-diabetes.csv", header=None, names=col_names)
pima.head()

pregnant    glucose  bp    skin  insulin  bmi   pedigree    age   label
0       6         148      72    35     0       33.6    0.627     50      1
1       1         85       66    29     0       26.6    0.351     31      0
2       8         183      64     0     0       23.3    0.672     32      1
3       1         89       66    23     94      28.1    0.167     21      0
4       0         137      40    35     168     43.1    2.288     33      1

Teilen Sie nun den Datensatz wie folgt in Features und Zielvariable auf:

feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variable

Als nächstes werden wir die Daten in Zug- und Testaufteilung aufteilen. Der folgende Code teilt den Datensatz in 70% Trainingsdaten und 30% Testdaten auf -

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

Als nächstes trainieren Sie das Modell mit Hilfe der DecisionTreeClassifier-Klasse von sklearn wie folgt:

clf = DecisionTreeClassifier()
clf = clf.fit(X_train,y_train)

Endlich müssen wir Vorhersagen treffen. Dies kann mit Hilfe des folgenden Skripts erfolgen:

y_pred = clf.predict(X_test)

Als nächstes können wir die Genauigkeitsbewertung, die Verwirrungsmatrix und den Klassifizierungsbericht wie folgt erhalten:

from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)

Ausgabe

Confusion Matrix:
[[116 30]
[ 46 39]]
Classification Report:
            precision   recall   f1-score    support
      0       0.72      0.79       0.75     146
      1       0.57      0.46       0.51     85
micro avg     0.67      0.67       0.67     231
macro avg     0.64      0.63       0.63     231
weighted avg  0.66      0.67       0.66     231

Accuracy: 0.670995670995671

Entscheidungsbaum visualisieren

Der obige Entscheidungsbaum kann mit Hilfe des folgenden Codes visualisiert werden:

from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus

dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
      filled=True, rounded=True,
      special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('Pima_diabetes_Tree.png')
Image(graph.create_png())