Clustering-Algorithmen - Hierarchisches Clustering

Einführung in das hierarchische Clustering

Hierarchisches Clustering ist ein weiterer unbeaufsichtigter Lernalgorithmus, mit dem die unbeschrifteten Datenpunkte mit ähnlichen Eigenschaften zusammengefasst werden. Hierarchische Clustering-Algorithmen lassen sich in zwei Kategorien einteilen:

Agglomerative hierarchical algorithms- In agglomerativen hierarchischen Algorithmen wird jeder Datenpunkt als einzelner Cluster behandelt und anschließend die Clusterpaare nacheinander zusammengeführt oder agglomeriert (Bottom-up-Ansatz). Die Hierarchie der Cluster wird als Dendrogramm oder Baumstruktur dargestellt.

Divisive hierarchical algorithms - Andererseits werden in divisiven hierarchischen Algorithmen alle Datenpunkte als ein großer Cluster behandelt, und beim Clustering wird der eine große Cluster in verschiedene kleine Cluster aufgeteilt (Top-down-Ansatz).

Schritte zum Durchführen eines agglomerativen hierarchischen Clusters

Wir werden das am häufigsten verwendete und wichtigste hierarchische Clustering erklären, dh das Agglomerativ. Die Schritte, um dasselbe auszuführen, sind wie folgt:

• Step 1- Behandeln Sie jeden Datenpunkt als einzelnen Cluster. Daher werden wir zu Beginn beispielsweise K-Cluster haben. Die Anzahl der Datenpunkte beträgt zu Beginn ebenfalls K.

• Step 2- In diesem Schritt müssen wir nun einen großen Cluster bilden, indem wir zwei Schrankdatenpunkte verbinden. Dies führt zu insgesamt K-1-Clustern.

• Step 3- Um mehr Cluster zu bilden, müssen wir zwei Closet-Cluster verbinden. Dies führt zu insgesamt K-2-Clustern.

• Step 4 - Um nun einen großen Cluster zu bilden, wiederholen Sie die obigen drei Schritte, bis K 0 wird, dh keine Datenpunkte mehr zum Verbinden übrig sind.

• Step 5 - Nach der Erstellung eines einzelnen großen Clusters werden Dendrogramme verwendet, um je nach Problem in mehrere Cluster zu unterteilen.

Rolle von Dendrogrammen bei der agglomerativen hierarchischen Clusterbildung

Wie wir im letzten Schritt besprochen haben, beginnt die Rolle des Dendrogramms, sobald sich der große Cluster gebildet hat. Das Dendrogramm wird verwendet, um die Cluster abhängig von unserem Problem in mehrere Cluster verwandter Datenpunkte aufzuteilen. Es kann anhand des folgenden Beispiels verstanden werden:

Beispiel 1

Um dies zu verstehen, beginnen wir mit dem Importieren der erforderlichen Bibliotheken wie folgt:

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

Als nächstes zeichnen wir die Datenpunkte, die wir für dieses Beispiel genommen haben -

X = np.array([[7,8],[12,20],[17,19],[26,15],[32,37],[87,75],[73,85], [62,80],[73,60],[87,96],])
labels = range(1, 11)
plt.figure(figsize=(10, 7))
plt.subplots_adjust(bottom=0.1)
plt.scatter(X[:,0],X[:,1], label='True Position')
for label, x, y in zip(labels, X[:, 0], X[:, 1]):
   plt.annotate(label,xy=(x, y), xytext=(-3, 3),textcoords='offset points', ha='right', va='bottom')
plt.show()

Aus dem obigen Diagramm ist sehr leicht ersichtlich, dass wir zwei Cluster in unseren Datenpunkten haben, aber in den Daten der realen Welt können Tausende von Clustern vorhanden sein. Als nächstes zeichnen wir die Dendrogramme unserer Datenpunkte mithilfe der Scipy-Bibliothek -

from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
linked = linkage(X, 'single')
labelList = range(1, 11)
plt.figure(figsize=(10, 7))
dendrogram(linked, orientation='top',labels=labelList, distance_sort='descending',show_leaf_counts=True)
plt.show()

Sobald der große Cluster gebildet ist, wird der längste vertikale Abstand ausgewählt. Eine vertikale Linie wird dann durch sie gezogen, wie in der folgenden Abbildung gezeigt. Wenn die horizontale Linie an zwei Punkten die blaue Linie kreuzt, beträgt die Anzahl der Cluster zwei.

Als Nächstes müssen wir die Klasse für das Clustering importieren und ihre Methode fit_predict aufrufen, um den Cluster vorherzusagen. Wir importieren die AgglomerativeClustering-Klasse der sklearn.cluster-Bibliothek -

from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
cluster.fit_predict(X)

Zeichnen Sie als Nächstes den Cluster mithilfe des folgenden Codes:

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='rainbow')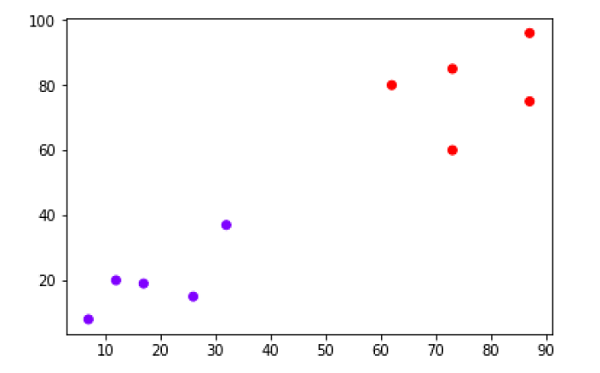

Das obige Diagramm zeigt die beiden Cluster aus unseren Datenpunkten.

Beispiel2

Nachdem wir das Konzept der Dendrogramme anhand des oben diskutierten einfachen Beispiels verstanden haben, gehen wir zu einem anderen Beispiel über, in dem wir Cluster des Datenpunkts im Pima Indian Diabetes Dataset mithilfe hierarchischer Cluster erstellen.

import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
import numpy as np
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
data.shape
(768, 9)
data.head()

Sl. Nein.	preg	Plas	Pres	Haut	Prüfung	Masse	pedi	Alter	Klasse
0	6	148	72	35	0	33.6	0,627	50	1
1	1	85	66	29	0	26.6	0,351	31	0
2	8	183	64	0	0	23.3	0,672	32	1
3	1	89	66	23	94	28.1	0,167	21	0
4	0	137	40	35	168	43.1	2.288	33	1

patient_data = data.iloc[:, 3:5].values
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 7))
plt.title("Patient Dendograms")
dend = shc.dendrogram(shc.linkage(data, method='ward'))

from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=4, affinity='euclidean', linkage='ward')
cluster.fit_predict(patient_data)
plt.figure(figsize=(10, 7))
plt.scatter(patient_data[:,0], patient_data[:,1], c=cluster.labels_, cmap='rainbow')