MATLAB - Kalkül

MATLAB bietet verschiedene Möglichkeiten zur Lösung von Problemen der Differential- und Integralrechnung, zur Lösung von Differentialgleichungen beliebigen Grades und zur Berechnung von Grenzwerten. Das Beste ist, dass Sie die Diagramme komplexer Funktionen einfach zeichnen und Maxima, Minima und andere Schreibwarenpunkte in einem Diagramm überprüfen können, indem Sie die ursprüngliche Funktion sowie deren Ableitung lösen.

Dieses Kapitel befasst sich mit Kalkülproblemen. In diesem Kapitel werden Vorberechnungskonzepte erörtert, dh das Berechnen von Funktionsgrenzen und das Überprüfen der Eigenschaften von Grenzen.

Im nächsten Kapitel Differential berechnen wir die Ableitung eines Ausdrucks und finden die lokalen Maxima und Minima in einem Diagramm. Wir werden auch das Lösen von Differentialgleichungen diskutieren.

Schließlich werden wir im Kapitel Integration die Integralrechnung diskutieren.

Grenzwerte berechnen

MATLAB bietet die limitFunktion zur Berechnung von Grenzwerten. In seiner grundlegendsten Form ist dielimit Die Funktion nimmt den Ausdruck als Argument und findet die Grenze des Ausdrucks, wenn die unabhängige Variable auf Null geht.

Berechnen wir zum Beispiel die Grenze einer Funktion f (x) = (x ³ + 5) / (x ⁴ + 7), da x gegen Null geht.

syms x
limit((x^3 + 5)/(x^4 + 7))

MATLAB führt die obige Anweisung aus und gibt das folgende Ergebnis zurück:

ans =
   5/7

Die Grenzwertfunktion fällt in den Bereich des symbolischen Rechnens; Sie müssen die verwendensymsFunktion, um MATLAB mitzuteilen, welche symbolischen Variablen Sie verwenden. Sie können auch das Limit einer Funktion berechnen, da die Variable zu einer anderen Zahl als Null tendiert. Um lim _{x-> a} (f (x)) zu berechnen , verwenden wir den Befehl limit mit Argumenten. Der erste ist der Ausdruck und der zweite ist die Zahl, der sich x nähert, hier ist es a .

Berechnen wir zum Beispiel die Grenze einer Funktion f (x) = (x-3) / (x-1), da x gegen 1 tendiert.

limit((x - 3)/(x-1),1)

MATLAB führt die obige Anweisung aus und gibt das folgende Ergebnis zurück:

ans =
   NaN

Nehmen wir ein anderes Beispiel:

limit(x^2 + 5, 3)

MATLAB führt die obige Anweisung aus und gibt das folgende Ergebnis zurück:

ans =
   14

Grenzwerte mit Oktave berechnen

Es folgt die Octave-Version des obigen Beispiels mit symbolic Paket, versuchen Sie, das Ergebnis auszuführen und zu vergleichen -

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Octave führt die obige Anweisung aus und gibt das folgende Ergebnis zurück:

ans =
   0.7142857142857142857

Überprüfung der grundlegenden Eigenschaften von Grenzwerten

Der algebraische Grenzwertsatz bietet einige grundlegende Eigenschaften von Grenzwerten. Diese sind wie folgt -

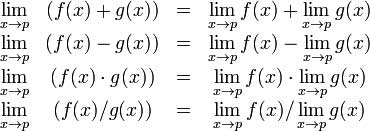
Betrachten wir zwei Funktionen -

f (x) = (3x + 5) / (x - 3)
g (x) = x ² + 1.

Berechnen wir die Grenzen der Funktionen, da x gegen 5 tendiert, beider Funktionen und überprüfen Sie die grundlegenden Eigenschaften der Grenzen mit diesen beiden Funktionen und MATLAB.

Beispiel

Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein:

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

Wenn Sie die Datei ausführen, wird Folgendes angezeigt:

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

Überprüfung der grundlegenden Eigenschaften von Grenzwerten mit Octave

Es folgt die Octave-Version des obigen Beispiels mit symbolic Paket, versuchen Sie, das Ergebnis auszuführen und zu vergleichen -

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Octave führt die obige Anweisung aus und gibt das folgende Ergebnis zurück:

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

Linke und rechte Grenzen

Wenn eine Funktion für einen bestimmten Wert der Variablen eine Diskontinuität aufweist, ist die Grenze zu diesem Zeitpunkt nicht vorhanden. Mit anderen Worten, Grenzen einer Funktion f (x) haben eine Diskontinuität bei x = a, wenn der Wert der Grenze, wenn x sich x von links nähert, nicht gleich dem Wert der Grenze ist, wenn sich x von rechts nähert.

Dies führt zum Konzept der linkshändigen und rechtshändigen Grenzen. Eine linkshändige Grenze ist definiert als die Grenze als x -> a von links, dh x nähert sich a für Werte von x <a. Eine rechtshändige Grenze ist definiert als die Grenze als x -> a von rechts, dh x nähert sich a für Werte von x> a. Wenn das Limit für Linkshänder und das Limit für Rechtshänder nicht gleich sind, existiert das Limit nicht.

Betrachten wir eine Funktion -

f(x) = (x - 3)/|x - 3|

Wir werden zeigen, dass lim _{x-> 3} f (x) nicht existiert. MATLAB hilft uns, diese Tatsache auf zwei Arten festzustellen -

Durch Zeichnen des Funktionsgraphen und Anzeigen der Diskontinuität.
Indem Sie die Grenzen berechnen und zeigen, dass beide unterschiedlich sind.

Die Grenzwerte für Linkshänder und Rechtshänder werden berechnet, indem die Zeichenfolgen 'left' und 'right' als letztes Argument an den Befehl limit übergeben werden.

Beispiel

Erstellen Sie eine Skriptdatei und geben Sie den folgenden Code ein:

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

Wenn Sie die Datei ausführen, zeichnet MATLAB das folgende Diagramm

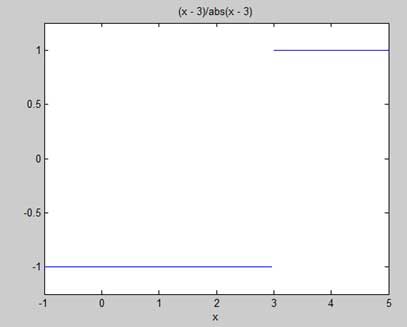
Danach wird folgende Ausgabe angezeigt -

l =
   -1
  
r =
   1