MATLAB - Operatoren
Ein Operator ist ein Symbol, das den Compiler anweist, bestimmte mathematische oder logische Manipulationen durchzuführen. MATLAB wurde entwickelt, um hauptsächlich mit ganzen Matrizen und Arrays zu arbeiten. Daher arbeiten Operatoren in MATLAB sowohl mit skalaren als auch mit nicht skalaren Daten. MATLAB erlaubt die folgenden Arten von Elementaroperationen -
- Rechenzeichen
- Vergleichsoperatoren
- Logische Operatoren
- Bitweise Operationen
- Operationen einstellen
Rechenzeichen
MATLAB erlaubt zwei verschiedene Arten von arithmetischen Operationen -
- Matrixarithmetische Operationen
- Array-Arithmetikoperationen
Matrixarithmetische Operationen sind dieselben wie in der linearen Algebra definiert. Array-Operationen werden Element für Element sowohl auf eindimensionalen als auch auf mehrdimensionalen Arrays ausgeführt.
Die Matrixoperatoren und Arrayoperatoren werden durch das Punktsymbol (.) Unterscheidet. Da jedoch die Additions- und Subtraktionsoperation für Matrizen und Arrays gleich ist, ist der Operator für beide Fälle gleich. Die folgende Tabelle enthält eine kurze Beschreibung der Bediener -
Beispiele anzeigen
| Sr.Nr. | Betreiber & Beschreibung |
|---|---|
| 1 | + Addition oder unäres Plus. A + B addiert die in den Variablen A und B gespeicherten Werte. A und B müssen dieselbe Größe haben, es sei denn, einer ist ein Skalar. Ein Skalar kann zu einer Matrix beliebiger Größe hinzugefügt werden. |
| 2 | - Subtraktion oder unäres Minus. AB subtrahiert den Wert von B von A. A und B müssen dieselbe Größe haben, es sei denn, man ist ein Skalar. Ein Skalar kann von einer Matrix beliebiger Größe subtrahiert werden. |
| 3 | * Matrix-Multiplikation. C = A * B ist das lineare algebraische Produkt der Matrizen A und B. Genauer gesagt:
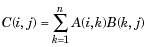
Für nicht skalare A und B muss die Anzahl der Spalten von A gleich der Anzahl der Zeilen von B sein. Ein Skalar kann eine Matrix beliebiger Größe multiplizieren. |
| 4 | .* Array-Multiplikation. A. * B ist das Element-für-Element-Produkt der Arrays A und B. A und B müssen dieselbe Größe haben, es sei denn, eines davon ist ein Skalar. |
| 5 | / Schrägstrich oder Matrix rechts Teilung. B / A ist ungefähr das gleiche wie B * inv (A). Genauer gesagt ist B / A = (A '\ B') '. |
| 6 | ./ Array rechte Teilung. A./B ist die Matrix mit den Elementen A (i, j) / B (i, j). A und B müssen dieselbe Größe haben, es sei denn, einer von ihnen ist ein Skalar. |
| 7 | \ Backslash oder Matrix linke Teilung. Wenn A eine quadratische Matrix ist, ist A \ B ungefähr dasselbe wie inv (A) * B, außer dass es auf eine andere Weise berechnet wird. Wenn A eine n-mal-n - Matrix ist und B ist ein Spaltenvektor mit N Komponenten oder eine Matrix mit mehreren solchen Säulen, dann X = A \ B ist die Lösung für die Gleichung AX = B . Eine Warnmeldung wird angezeigt, wenn A schlecht skaliert oder nahezu singulär ist. |
| 8 | .\ Array linke Teilung. A. \ B ist die Matrix mit den Elementen B (i, j) / A (i, j). A und B müssen dieselbe Größe haben, es sei denn, einer von ihnen ist ein Skalar. |
| 9 | ^ Matrixleistung. X ^ p ist X zur Potenz p, wenn p ein Skalar ist. Wenn p eine ganze Zahl ist, wird die Potenz durch wiederholtes Quadrieren berechnet. Wenn die Ganzzahl negativ ist, wird X zuerst invertiert. Für andere Werte von p beinhaltet die Berechnung Eigenwerte und Eigenvektoren, so dass wenn [V, D] = eig (X), dann X ^ p = V * D. ^ p / V. |
| 10 | .^ Array-Leistung. A. ^ B ist die Matrix mit den Elementen A (i, j) zur Potenz B (i, j). A und B müssen dieselbe Größe haben, es sei denn, einer von ihnen ist ein Skalar. |
| 11 | ' Matrix transponieren. A 'ist die lineare algebraische Transponierte von A. Für komplexe Matrizen ist dies die komplexe konjugierte Transponierte. |
| 12 | .' Array transponieren. EIN.' ist die Array-Transponierte von A. Für komplexe Matrizen beinhaltet dies keine Konjugation. |
Vergleichsoperatoren
Vergleichsoperatoren können auch sowohl skalare als auch nicht skalare Daten bearbeiten. Vergleichsoperatoren für Arrays führen Element-für-Element-Vergleiche zwischen zwei Arrays durch und geben ein logisches Array derselben Größe zurück, wobei Elemente auf logisch 1 (wahr) gesetzt sind, wobei die Beziehung wahr ist, und Elemente auf logisch 0 (falsch) gesetzt sind, wo sie ist nicht.
Die folgende Tabelle zeigt die in MATLAB verfügbaren Vergleichsoperatoren -
Beispiele anzeigen
| Sr.Nr. | Betreiber & Beschreibung |
|---|---|
| 1 | < Weniger als |
| 2 | <= Gleich oder kleiner als |
| 3 | > Größer als |
| 4 | >= Größer als oder gleich wie |
| 5 | == Gleicht |
| 6 | ~= Nicht gleichzusetzen mit |
Logische Operatoren
MATLAB bietet zwei Arten von logischen Operatoren und Funktionen:
Elementweise - Diese Operatoren bearbeiten entsprechende Elemente logischer Arrays.
Kurzschluss - Diese Operatoren arbeiten mit skalaren und logischen Ausdrücken.
Elementweise logische Operatoren arbeiten Element für Element auf logischen Arrays. Die Symbole &, | und ~ sind die logischen Array-Operatoren AND, OR und NOT.
Logische Kurzschlussoperatoren ermöglichen das Kurzschließen logischer Operationen. Die Symbole && und || sind die logischen Kurzschlussoperatoren AND und OR.
Beispiele anzeigen
Bitweise Operationen
Bitweise Operatoren arbeiten an Bits und führen eine bitweise Operation durch. Die Wahrheitstabellen für &, | und ^ lauten wie folgt:
| p | q | p & q | p | q | p ^ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Angenommen, A = 60; und B = 13; Jetzt im Binärformat werden sie wie folgt sein:
A = 0011 1100
B = 0000 1101
-----------------
A & B = 0000 1100
A | B = 0011 1101
A ^ B = 0011 0001
~ A = 1100 0011
MATLAB bietet verschiedene Funktionen für bitweise Operationen wie 'bitweise und', 'bitweise oder' und 'bitweise nicht' Operationen, Verschiebungsoperationen usw.
Die folgende Tabelle zeigt die häufig verwendeten bitweisen Operationen -
Beispiele anzeigen
| Funktion | Zweck |
|---|---|
| Bitand (a, b) | Bitweise UND von ganzen Zahlen a und b |
| bitcmp (a) | Bitweise Ergänzung von a |
| Bitget (a, pos) | Holen Sie sich das Bit an der angegebenen Position pos im Integer-Array a |
| Bitor (a, b) | Bitweises ODER der ganzen Zahlen a und b |
| Bitset (a, pos) | Setzen Sie das Bit an einer bestimmten Stelle pos von a |
| Bitverschiebung (a, k) | Gibt eine Verschiebung nach links um k Bits zurück, was einer Multiplikation mit 2 k entspricht . Negative Werte von k entsprechen dem Verschieben von Bits nach rechts oder dem Teilen durch 2 | k | und auf die nächste ganze Zahl in Richtung negativer Unendlichkeit runden. Alle Überlaufbits werden abgeschnitten. |
| Bitxor (a, b) | Bitweises XOR der ganzen Zahlen a und b |
| Swapbytes | Byte-Reihenfolge tauschen |
Operationen einstellen
MATLAB bietet verschiedene Funktionen für Mengenoperationen wie Vereinigung, Schnittmenge und Testen der Mengenmitgliedschaft usw.
Die folgende Tabelle zeigt einige häufig verwendete Set-Operationen -
Beispiele anzeigen
| Sr.Nr. | Bedienungsanleitung |
|---|---|
| 1 | intersect(A,B) Schnittpunkt zweier Arrays festlegen; Gibt die Werte zurück, die sowohl A als auch B gemeinsam sind. Die zurückgegebenen Werte sind in sortierter Reihenfolge. |
| 2 | intersect(A,B,'rows') Behandelt jede Zeile von A und jede Zeile von B als einzelne Entitäten und gibt die Zeilen zurück, die sowohl A als auch B gemeinsam sind. Die Zeilen der zurückgegebenen Matrix sind in sortierter Reihenfolge. |
| 3 | ismember(A,B) Gibt ein Array mit der gleichen Größe wie A zurück, das 1 (true) enthält, wobei sich die Elemente von A in B befinden. An anderer Stelle wird 0 (false) zurückgegeben. |
| 4 | ismember(A,B,'rows') Behandelt jede Zeile von A und jede Zeile von B als einzelne Entitäten und gibt einen Vektor zurück, der 1 (wahr) enthält, wobei die Zeilen der Matrix A auch Zeilen von B sind. An anderer Stelle wird 0 (falsch) zurückgegeben. |
| 5 | issorted(A) Gibt logische 1 (wahr) zurück, wenn die Elemente von A in sortierter Reihenfolge sind, andernfalls logische 0 (falsch). Eingabe A kann ein Vektor oder ein N-mal-1- oder 1-mal-N-Zellenarray von Strings sein.A is considered to be sorted if A und die Ausgabe von sort (A) sind gleich. |
| 6 | issorted(A, 'rows') Gibt logische 1 (wahr) zurück, wenn die Zeilen der zweidimensionalen Matrix A in sortierter Reihenfolge vorliegen, andernfalls logische 0 (falsch). Matrix A is considered to be sorted if A und die Ausgabe von Sortrows (A) ist gleich. |
| 7 | setdiff(A,B) Legt die Differenz zweier Arrays fest. Gibt die Werte in A zurück, die nicht in B sind. Die Werte im zurückgegebenen Array sind in sortierter Reihenfolge. |
| 8 | setdiff(A,B,'rows') Behandelt jede Zeile von A und jede Zeile von B als einzelne Entitäten und gibt die Zeilen von A zurück, die nicht in B sind. Die Zeilen der zurückgegebenen Matrix sind in sortierter Reihenfolge. Die Option 'Zeilen' unterstützt keine Zellenarrays. |
| 9 | setxor Legt das exklusive ODER von zwei Arrays fest |
| 10 | union Legt die Vereinigung zweier Arrays fest |
| 11 | unique Eindeutige Werte im Array |