TensorFlow - Diagramme erstellen
Eine partielle Differentialgleichung (PDE) ist eine Differentialgleichung, die partielle Ableitungen mit unbekannter Funktion mehrerer unabhängiger Variablen beinhaltet. In Bezug auf partielle Differentialgleichungen konzentrieren wir uns auf die Erstellung neuer Diagramme.
Nehmen wir an, es gibt einen Teich mit der Größe 500 * 500 Quadrat -
N = 500
Nun werden wir die partielle Differentialgleichung berechnen und daraus den jeweiligen Graphen bilden. Beachten Sie die unten angegebenen Schritte zur Berechnung des Diagramms.
Step 1 - Importieren Sie Bibliotheken für die Simulation.
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as pltStep 2 - Fügen Sie Funktionen zur Transformation eines 2D-Arrays in einen Faltungskern und eine vereinfachte 2D-Faltungsoperation hinzu.
def make_kernel(a):
a = np.asarray(a)
a = a.reshape(list(a.shape) + [1,1])
return tf.constant(a, dtype=1)
def simple_conv(x, k):
"""A simplified 2D convolution operation"""
x = tf.expand_dims(tf.expand_dims(x, 0), -1)
y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding = 'SAME')
return y[0, :, :, 0]
def laplace(x):
"""Compute the 2D laplacian of an array"""
laplace_k = make_kernel([[0.5, 1.0, 0.5], [1.0, -6., 1.0], [0.5, 1.0, 0.5]])
return simple_conv(x, laplace_k)
sess = tf.InteractiveSession()Step 3 - Geben Sie die Anzahl der Iterationen an und berechnen Sie das Diagramm, um die Datensätze entsprechend anzuzeigen.
N = 500
# Initial Conditions -- some rain drops hit a pond
# Set everything to zero
u_init = np.zeros([N, N], dtype = np.float32)
ut_init = np.zeros([N, N], dtype = np.float32)
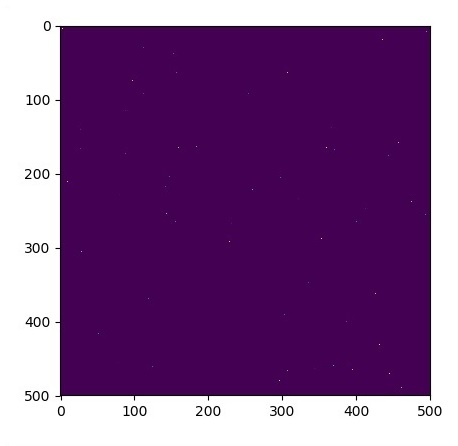
# Some rain drops hit a pond at random points
for n in range(100):
a,b = np.random.randint(0, N, 2)
u_init[a,b] = np.random.uniform()
plt.imshow(u_init)
plt.show()
# Parameters:
# eps -- time resolution
# damping -- wave damping
eps = tf.placeholder(tf.float32, shape = ())
damping = tf.placeholder(tf.float32, shape = ())
# Create variables for simulation state
U = tf.Variable(u_init)
Ut = tf.Variable(ut_init)
# Discretized PDE update rules
U_ = U + eps * Ut
Ut_ = Ut + eps * (laplace(U) - damping * Ut)
# Operation to update the state
step = tf.group(U.assign(U_), Ut.assign(Ut_))
# Initialize state to initial conditions
tf.initialize_all_variables().run()
# Run 1000 steps of PDE
for i in range(1000):
# Step simulation
step.run({eps: 0.03, damping: 0.04})
# Visualize every 50 steps
if i % 500 == 0:
plt.imshow(U.eval())
plt.show()Die Grafiken sind wie folgt dargestellt: