DAA - Arbres de recherche binaires à coût optimal
Un arbre de recherche binaire (BST) est un arbre dans lequel les valeurs de clé sont stockées dans les nœuds internes. Les nœuds externes sont des nœuds nuls. Les clés sont ordonnées lexicographiquement, c'est-à-dire que pour chaque nœud interne, toutes les clés du sous-arbre de gauche sont inférieures aux clés du nœud, et toutes les clés du sous-arbre de droite sont plus grandes.
Lorsque nous connaissons la fréquence de recherche de chacune des clés, il est assez facile de calculer le coût attendu d'accès à chaque nœud de l'arbre. Un arbre de recherche binaire optimal est un BST, qui a un coût attendu minimal pour localiser chaque nœud
Le temps de recherche d'un élément dans un BST est O(n), alors que dans un temps de recherche Balanced-BST est O(log n). Encore une fois, le temps de recherche peut être amélioré dans l'arbre de recherche binaire à coût optimal, en plaçant les données les plus fréquemment utilisées à la racine et plus près de l'élément racine, tout en plaçant les données les moins fréquemment utilisées près des feuilles et dans les feuilles.
Ici, l'algorithme optimal d'arbre de recherche binaire est présenté. Tout d'abord, nous construisons un BST à partir d'un ensemble den nombre de clés distinctes < k1, k2, k3, ... kn >. Ici, nous supposons, la probabilité d'accéder à une cléKi est pi. Quelques clés factices (d0, d1, d2, ... dn) sont ajoutés car certaines recherches peuvent être effectuées pour les valeurs qui ne sont pas présentes dans l'ensemble de clés K. Nous supposons, pour chaque clé facticedi la probabilité d'accès est qi.
Optimal-Binary-Search-Tree(p, q, n)
e[1…n + 1, 0…n],
w[1…n + 1, 0…n],
root[1…n + 1, 0…n]
for i = 1 to n + 1 do
e[i, i - 1] := qi - 1
w[i, i - 1] := qi - 1
for l = 1 to n do
for i = 1 to n – l + 1 do
j = i + l – 1 e[i, j] := ∞
w[i, i] := w[i, i -1] + pj + qj
for r = i to j do
t := e[i, r - 1] + e[r + 1, j] + w[i, j]
if t < e[i, j]
e[i, j] := t
root[i, j] := r
return e and rootUne analyse
L'algorithme nécessite O (n3) temps, depuis trois imbriqués fordes boucles sont utilisées. Chacune de ces boucles prend au plusn valeurs.
Exemple
Compte tenu de l'arbre suivant, le coût est de 2,80, bien que ce ne soit pas un résultat optimal.
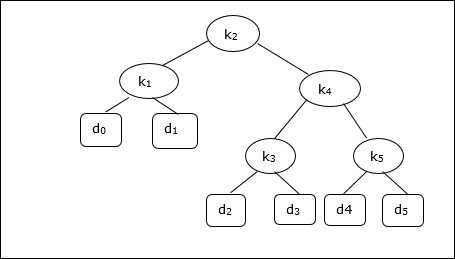
| Nœud | Profondeur | Probabilité | Contribution |
|---|---|---|---|
| k 1 | 1 | 0,15 | 0,30 |
| k 2 | 0 | 0,10 | 0,10 |
| k 3 | 2 | 0,05 | 0,15 |
| k 4 | 1 | 0,10 | 0,20 |
| k 5 | 2 | 0,20 | 0,60 |
| d 0 | 2 | 0,05 | 0,15 |
| d 1 | 2 | 0,10 | 0,30 |
| d 2 | 3 | 0,05 | 0,20 |
| d 3 | 3 | 0,05 | 0,20 |
| d 4 | 3 | 0,05 | 0,20 |
| d 5 | 3 | 0,10 | 0,40 |
| Total | 2,80 |
Pour obtenir une solution optimale, en utilisant l'algorithme décrit dans ce chapitre, les tableaux suivants sont générés.
Dans les tableaux suivants, l'index de colonne est i et l'index de ligne est j.
| e | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 5 | 2,75 | 2,00 | 1,30 | 0,90 | 0,50 | 0,10 |
| 4 | 1,75 | 1,20 | 0,60 | 0,30 | 0,05 | |
| 3 | 1,25 | 0,70 | 0,25 | 0,05 | ||
| 2 | 0,90 | 0,40 | 0,05 | |||
| 1 | 0,45 | 0,10 | ||||
| 0 | 0,05 |
| w | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 5 | 1,00 | 0,80 | 0,60 | 0,50 | 0,35 | 0,10 |
| 4 | 0,70 | 0,50 | 0,30 | 0,20 | 0,05 | |
| 3 | 0,55 | 0,35 | 0,15 | 0,05 | ||
| 2 | 0,45 | 0,25 | 0,05 | |||
| 1 | 0,30 | 0,10 | ||||
| 0 | 0,05 |
| racine | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 5 | 2 | 4 | 5 | 5 | 5 |
| 4 | 2 | 2 | 4 | 4 | |
| 3 | 2 | 2 | 3 | ||
| 2 | 1 | 2 | |||
| 1 | 1 |
À partir de ces tables, l'arbre optimal peut être formé.