DAA - Couverture Vertex

Une couverture de sommet d'un graphe non orienté G = (V, E) est un sous-ensemble de sommets V^' ⊆ V tel que si bord (u, v) est un bord de G, alors soit u dans V ou v dans V^' ou les deux.

Trouvez une couverture de sommet de taille maximale dans un graphe non orienté donné. Ce vertexcover optimal est la version d'optimisation d'un problème NP-complet. Cependant, il n'est pas trop difficile de trouver une couverture de sommets presque optimale.

APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G] 
while E' is not empty do 
   Let (u, v) be an arbitrary edge of E' c ← c U {u, v} 
   Remove from E' every edge incident on either u or v 
return c

Exemple

L'ensemble des arêtes du graphe donné est -

{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}

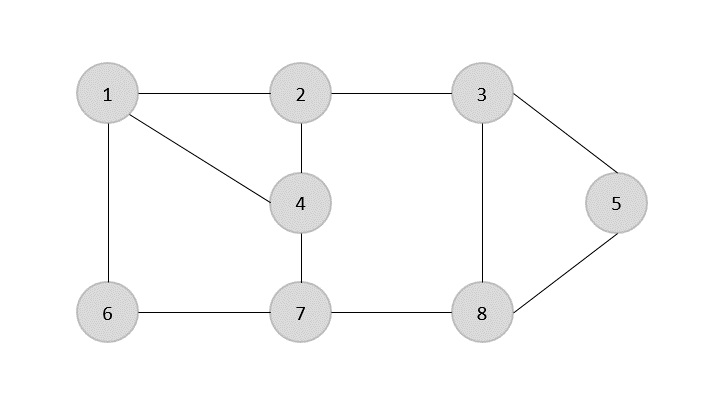
Maintenant, nous commençons par sélectionner une arête arbitraire (1,6). Nous éliminons toutes les arêtes, qui sont soit incidentes au sommet 1 ou 6 et nous ajoutons l'arête (1,6) à couvrir.

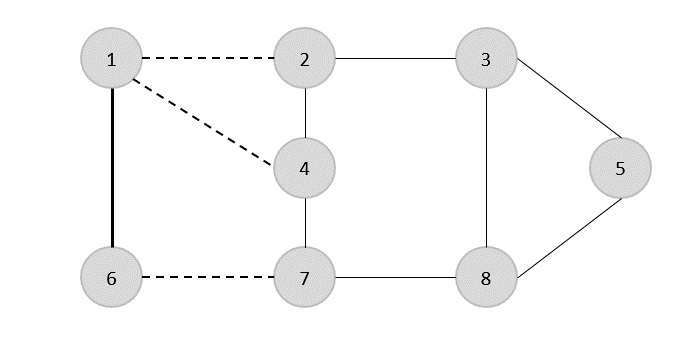
Dans l'étape suivante, nous avons choisi une autre arête (2,3) au hasard

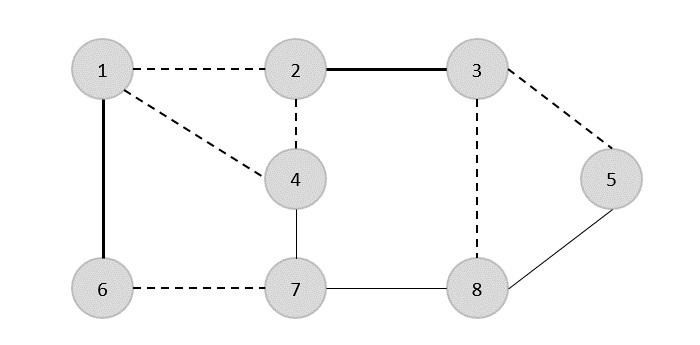
Maintenant, nous sélectionnons une autre arête (4,7).

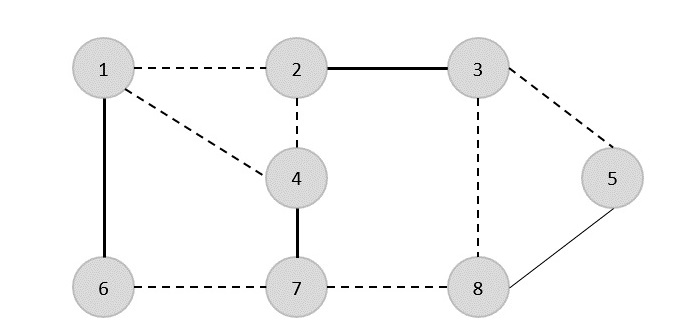
Nous sélectionnons une autre arête (8,5).

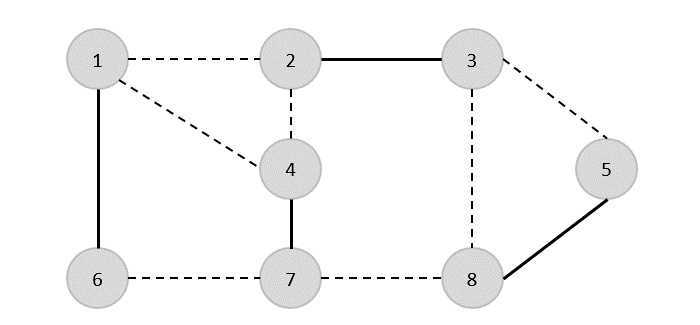
Par conséquent, la couverture des sommets de ce graphe est {1,2,4,5}.

Une analyse

Il est facile de voir que le temps d'exécution de cet algorithme est O(V + E), en utilisant la liste de contiguïté pour représenter E^'.