DAA - Arbre couvrant

UNE spanning tree est un sous-ensemble d'un graphe non orienté dont tous les sommets sont reliés par un nombre minimum d'arêtes.

Si tous les sommets sont connectés dans un graphe, alors il existe au moins un arbre couvrant. Dans un graphique, il peut exister plus d'un arbre couvrant.

Propriétés

Un Spanning Tree n'a pas de cycle.
Tout sommet peut être atteint à partir de n'importe quel autre sommet.

Exemple

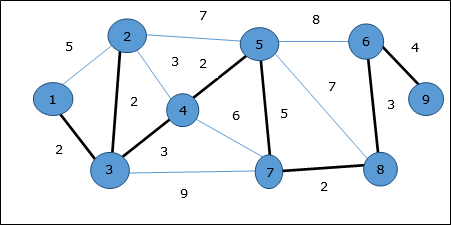
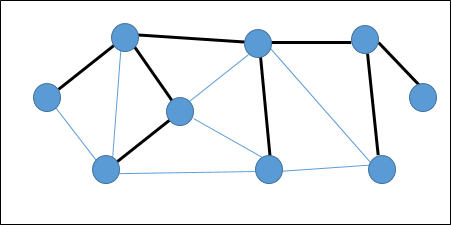
Dans le graphique suivant, les arêtes en surbrillance forment un arbre couvrant.

Arbre couvrant minimum

UNE Minimum Spanning Tree (MST)est un sous-ensemble d'arêtes d'un graphe non orienté pondéré connecté qui relie tous les sommets avec le poids d'arête total minimum possible. Pour dériver un MST, l'algorithme de Prim ou l'algorithme de Kruskal peut être utilisé. Par conséquent, nous discuterons de l'algorithme de Prim dans ce chapitre.

Comme nous l'avons vu, un graphe peut avoir plus d'un arbre couvrant. S'il y an nombre de sommets, l'arbre couvrant doit avoir n - 1nombre d'arêtes. Dans ce contexte, si chaque arête du graphe est associée à un poids et qu'il existe plus d'un arbre couvrant, nous devons trouver l'arbre couvrant minimum du graphe.

De plus, s'il existe des arêtes pondérées en double, le graphe peut avoir plusieurs arbres couvrant minimum.

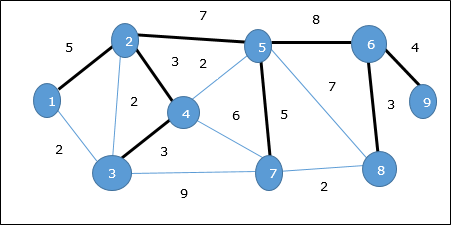
Dans le graphique ci-dessus, nous avons montré un arbre couvrant bien qu'il ne s'agisse pas de l'arbre couvrant minimum. Le coût de cet arbre couvrant est (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38.

Nous utiliserons l'algorithme de Prim pour trouver l'arbre couvrant minimum.

Algorithme de Prim

L'algorithme de Prim est une approche gourmande pour trouver l'arbre couvrant minimum. Dans cet algorithme, pour former un MST, nous pouvons partir d'un sommet arbitraire.

Algorithm: MST-Prim’s (G, w, r) 
for each u є G.V 
   u.key = ∞ 
   u.∏ = NIL 
r.key = 0 
Q = G.V 
while Q ≠ Ф 
   u = Extract-Min (Q) 
   for each v є G.adj[u] 
      if each v є Q and w(u, v) < v.key 
         v.∏ = u 
         v.key = w(u, v)

La fonction Extract-Min renvoie le sommet avec un coût d'arête minimum. Cette fonction fonctionne sur min-heap.

Exemple

En utilisant l'algorithme de Prim, nous pouvons partir de n'importe quel sommet, commençons par un sommet 1.

Sommet 3 est connecté au sommet 1 avec un coût de bord minimal, donc un bord (1, 2) est ajouté à l'arbre couvrant.

Ensuite, bord (2, 3) est considéré car c'est le minimum parmi les arêtes {(1, 2), (2, 3), (3, 4), (3, 7)}.

Dans la prochaine étape, nous avons l'avantage (3, 4) et (2, 4)avec un coût minimum. Bord(3, 4) est sélectionné au hasard.

De la même manière, les bords (4, 5), (5, 7), (7, 8), (6, 8) et (6, 9)sont sélectionnés. Comme tous les sommets sont visités, l'algorithme s'arrête maintenant.

Le coût de l'arbre couvrant est (2 + 2 + 3 + 2 + 5 + 2 + 3 + 4) = 23. Il n'y a plus d'arbre couvrant dans ce graphique avec un coût inférieur à 23.