DAA - Chemins les plus courts

Algorithme de Dijkstra

L'algorithme de Dijkstra résout le problème des chemins les plus courts à source unique sur un graphe pondéré dirigé G = (V, E) , où toutes les arêtes sont non négatives (c'est-à-dire w (u, v) ≥ 0 pour chaque arête (u, v ) Є E ).

Dans l'algorithme suivant, nous utiliserons une fonction Extract-Min(), qui extrait le nœud avec la plus petite clé.

Algorithm: Dijkstra’s-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
S := Ф 
Q := G.V 
while Q ≠ Ф 
   u := Extract-Min (Q) 
   S := S U {u} 
   for each vertex v Є G.adj[u] 
      if v.d > u.d + w(u, v) 
         v.d := u.d + w(u, v) 
         v.∏ := u

Une analyse

La complexité de cet algorithme dépend entièrement de l'implémentation de la fonction Extract-Min. Si la fonction d'extraction min est implémentée en utilisant la recherche linéaire, la complexité de cet algorithme estO(V² + E).

Dans cet algorithme, si nous utilisons min-heap sur lequel Extract-Min() fonctionne pour renvoyer le nœud de Q avec la plus petite clé, la complexité de cet algorithme peut être réduite davantage.

Exemple

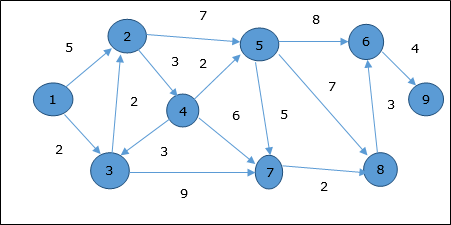
Considérons le sommet 1 et 9comme sommet de départ et de destination respectivement. Initialement, tous les sommets sauf le sommet de départ sont marqués par ∞ et le sommet de départ est marqué par0.

Sommet	Initiale	Étape 1 V 1	Étape 2 V 3	Étape 3 V 2	Étape 4 V 4	Étape 5 V 5	Étape 6 V 7	Étape 7 V 8	Étape 8 V 6
1	0	0	0	0	0	0	0	0	0
2	∞	5	4	4	4	4	4	4	4
3	∞	2	2	2	2	2	2	2	2
4	∞	∞	∞	sept	sept	sept	sept	sept	sept
5	∞	∞	∞	11	9	9	9	9	9
6	∞	∞	∞	∞	∞	17	17	16	16
sept	∞	∞	11	11	11	11	11	11	11
8	∞	∞	∞	∞	∞	16	13	13	13
9	∞	∞	∞	∞	∞	∞	∞	∞	20

Par conséquent, la distance minimale du sommet 9 du sommet 1 est 20. Et le chemin est

1 → 3 → 7 → 8 → 6 → 9

Ce chemin est déterminé en fonction des informations du prédécesseur.

Algorithme Bellman Ford

Cet algorithme résout le problème de chemin le plus court source unique d'un graphe orienté G = (V, E)dans lequel les poids des bords peuvent être négatifs. De plus, cet algorithme peut être appliqué pour trouver le chemin le plus court, s'il n'existe pas de cycle pondéré négatif.

Algorithm: Bellman-Ford-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
for i = 1 to |G.V| - 1 
   for each edge (u, v) Є G.E 
      if v.d > u.d + w(u, v) 
         v.d := u.d +w(u, v) 
         v.∏ := u 
for each edge (u, v) Є G.E 
   if v.d > u.d + w(u, v) 
      return FALSE 
return TRUE

Une analyse

La première for boucle est utilisée pour l'initialisation, qui s'exécute dans O(V)fois. Le suivantfor boucle s'exécute |V - 1| passe sur les bords, ce qui prendO(E) fois.

Par conséquent, l'algorithme de Bellman-Ford fonctionne dans O(V, E) temps.

Exemple

L'exemple suivant montre comment l'algorithme Bellman-Ford fonctionne étape par étape. Ce graphe a un bord négatif mais n'a pas de cycle négatif, le problème peut donc être résolu en utilisant cette technique.

Au moment de l'initialisation, tous les sommets sauf la source sont marqués par ∞ et la source est marquée par 0.

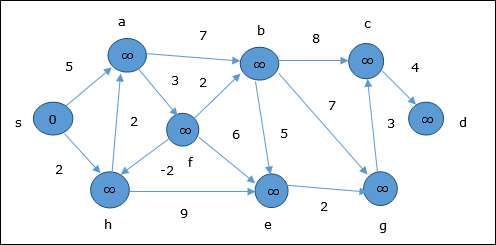
Dans un premier temps, tous les sommets accessibles depuis la source sont mis à jour au coût minimum. Par conséquent, les sommetsa et h sont mis à jour.

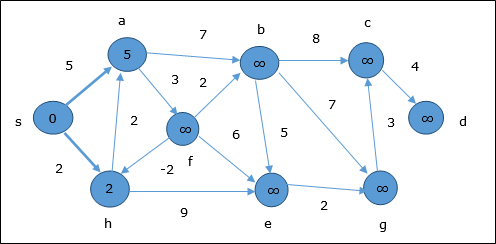
Dans l'étape suivante, les sommets a, b, f et e sont mis à jour.

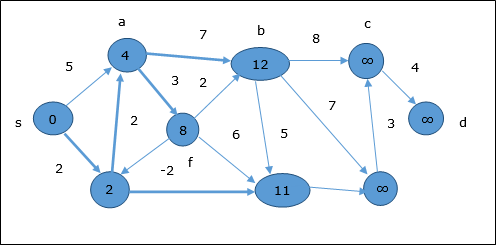
Suivant la même logique, dans cette étape les sommets b, f, c et g sont mis à jour.

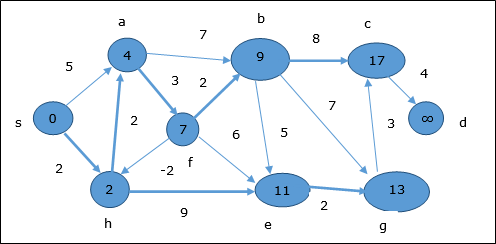
Ici, les sommets c et d sont mis à jour.

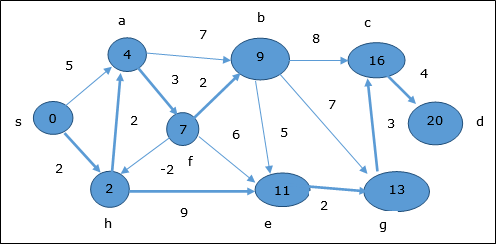
Par conséquent, la distance minimale entre les sommets s et sommet d est 20.

Sur la base des informations du prédécesseur, le chemin est s → h → e → g → c → d