Communication numérique - Modulation Delta
La fréquence d'échantillonnage d'un signal doit être supérieure à la fréquence de Nyquist, pour obtenir un meilleur échantillonnage. Si cet intervalle d'échantillonnage en PCM différentiel est considérablement réduit, la différence d'amplitude échantillon-échantillon est très petite, comme si la différence était1-bit quantization, alors la taille du pas sera très petite, c'est-à-dire, Δ (delta).
Modulation Delta
Le type de modulation, où la fréquence d'échantillonnage est beaucoup plus élevée et dans laquelle le pas après quantification est d'une valeur plus petite Δ, une telle modulation est appelée delta modulation.
Caractéristiques de la modulation delta
Voici quelques-unes des caractéristiques de la modulation delta.
Une entrée suréchantillonnée est utilisée pour utiliser pleinement la corrélation de signal.
La conception de la quantification est simple.
La séquence d'entrée est beaucoup plus élevée que le taux de Nyquist.
La qualité est modérée.
La conception du modulateur et du démodulateur est simple.
L'approximation en escalier de la forme d'onde de sortie.
La taille du pas est très petite, c'est-à-dire Δ (delta).
Le débit binaire peut être décidé par l'utilisateur.
Cela implique une mise en œuvre plus simple.
La modulation Delta est une forme simplifiée de la technique DPCM, également considérée comme 1-bit DPCM scheme. Lorsque l'intervalle d'échantillonnage est réduit, la corrélation du signal sera plus élevée.
Modulateur Delta
Le Delta Modulator comprend un quantificateur 1 bit et un circuit de retard ainsi que deux circuits d'été. Voici le schéma de principe d'un modulateur delta.
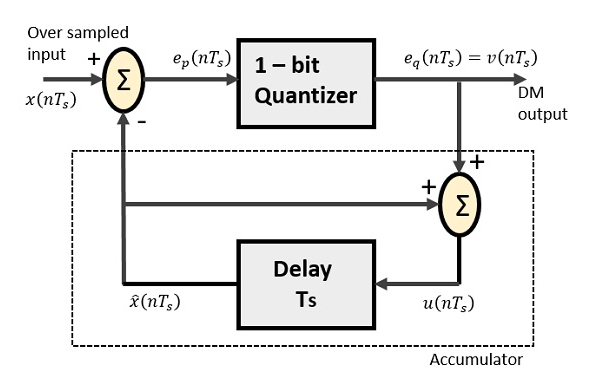
Le circuit prédicteur en DPCM est remplacé par un simple circuit à retard en DM.
À partir du diagramme ci-dessus, nous avons les notations comme -
$ x (nT_ {s}) $ = sur l'entrée échantillonnée
$ e_ {p} (nT_ {s}) $ = sortie d'été et entrée de quantificateur
$ e_ {q} (nT_ {s}) $ = sortie du quantificateur = $ v (nT_s) $
$ \ widehat {x} (nT_ {s}) $ = sortie du circuit de retard
$ u (nT_ {s}) $ = entrée du circuit de retard
En utilisant ces notations, nous allons maintenant essayer de comprendre le processus de modulation delta.
$ e_ {p} (nT_ {s}) = x (nT_ {s}) - \ widehat {x} (nT_ {s}) $
--------- équation 1
$ = x (nT_ {s}) - u ([n - 1] T_ {s}) $
$ = x (nT_ {s}) - [\ widehat {x} [[n - 1] T_ {s}] + v [[n-1] T_ {s}]] $
--------- équation 2
Plus loin,
$ v (nT_ {s}) = e_ {q} (nT_ {s}) = S.sig. [e_ {p} (nT_ {s})] $
--------- équation 3
$ u (nT_ {s}) = \ widehat {x} (nT_ {s}) + e_ {q} (nT_ {s}) $
Où,
$ \ widehat {x} (nT_ {s}) $ = la valeur précédente du circuit de retard
$ e_ {q} (nT_ {s}) $ = sortie du quantificateur = $ v (nT_s) $
Par conséquent,
$ u (nT_ {s}) = u ([n-1] T_ {s}) + v (nT_ {s}) $
--------- équation 4
Ce qui signifie,
The present input of the delay unit
= (The previous output of the delay unit) + (the present quantizer output)
En supposant une condition d'accumulation nulle,
$ u (nT_ {s}) = S \ Displaystyle \ sum \ limits_ {j = 1} ^ n sig [e_ {p} (jT_ {s})] $
Accumulated version of DM output = $ \ Displaystyle \ sum \ limits_ {j = 1} ^ nv (jT_ {s}) $
--------- équation 5
Maintenant, notez que
$ \ widehat {x} (nT_ {s}) = u ([n-1] T_ {s}) $
$ = \ Displaystyle \ sum \ limits_ {j = 1} ^ {n - 1} v (jT_ {s}) $
--------- équation 6
La sortie de l'unité de retard est une sortie de l'accumulateur retardée d'un échantillon.
À partir des équations 5 et 6, nous obtenons une structure possible pour le démodulateur.
Une forme d'onde approximative de cas d'escalier sera la sortie du modulateur delta avec la taille de pas comme delta (Δ). La qualité de sortie de la forme d'onde est moyenne.
Démodulateur Delta
Le démodulateur delta comprend un filtre passe-bas, un sommateur et un circuit de retard. Le circuit de prédiction est ici éliminé et par conséquent aucune entrée supposée n'est donnée au démodulateur.
Voici le diagramme du démodulateur delta.
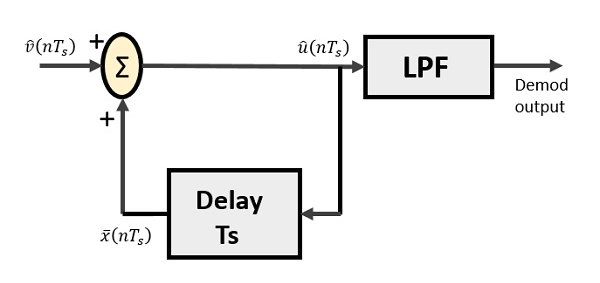
À partir du diagramme ci-dessus, nous avons les notations comme -
$ \ widehat {v} (nT_ {s}) $ est l'exemple d'entrée
$ \ widehat {u} (nT_ {s}) $ est la sortie d'été
$ \ bar {x} (nT_ {s}) $ est la sortie retardée
Une séquence binaire sera donnée en entrée du démodulateur. La sortie approximative de la cage d'escalier est donnée au LPF.
Le filtre passe-bas est utilisé pour de nombreuses raisons, mais la principale raison est l'élimination du bruit pour les signaux hors bande. L'erreur de taille de pas qui peut survenir au niveau de l'émetteur est appeléegranular noise, qui est éliminé ici. S'il n'y a pas de bruit, la sortie du modulateur est égale à l'entrée du démodulateur.
Avantages de DM sur DPCM
Quantificateur 1 bit
Conception très simple du modulateur et du démodulateur
Cependant, il existe un peu de bruit dans DM.
Pente Distorsion de surcharge (quand Δ est petite)
Bruit granulaire (quand Δ est large)
Modulation adaptative delta (ADM)
Dans la modulation numérique, nous avons rencontré un certain problème de détermination de la taille du pas, qui influence la qualité de l'onde de sortie.
Un pas plus grand est nécessaire dans la pente raide du signal de modulation et un pas plus petit est nécessaire là où le message a une petite pente. Les moindres détails sont manqués dans le processus. Ainsi, il serait préférable que nous puissions contrôler l'ajustement de la taille de pas, en fonction de nos besoins afin d'obtenir l'échantillonnage de la manière souhaitée. C'est le concept deAdaptive Delta Modulation.
Voici le schéma de principe du modulateur delta adaptatif.
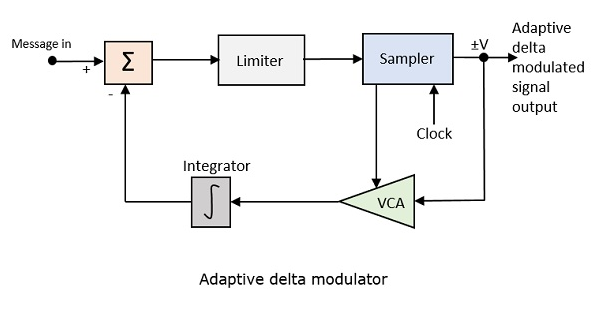
Le gain de l'amplificateur commandé en tension est ajusté par le signal de sortie de l'échantillonneur. Le gain de l'amplificateur détermine la taille du pas et les deux sont proportionnels.
ADM quantifie la différence entre la valeur de l'échantillon actuel et la valeur prédite de l'échantillon suivant. Il utilise une hauteur de pas variable pour prédire les valeurs suivantes, pour la reproduction fidèle des valeurs à variation rapide.