Communication numérique - Guide rapide
La communication qui se produit dans notre vie de tous les jours se fait sous forme de signaux. Ces signaux, tels que les signaux sonores, sont généralement de nature analogique. Lorsque la communication doit être établie à distance, les signaux analogiques sont envoyés par fil, en utilisant différentes techniques pour une transmission efficace.
La nécessité de la numérisation
Les méthodes de communication conventionnelles utilisaient des signaux analogiques pour les communications longue distance, qui souffrent de nombreuses pertes telles que distorsion, interférence et autres pertes, y compris une faille de sécurité.
Afin de surmonter ces problèmes, les signaux sont numérisés à l'aide de différentes techniques. Les signaux numérisés permettent à la communication d'être plus claire et précise sans pertes.
La figure suivante indique la différence entre les signaux analogiques et numériques. Les signaux numériques sont constitués de1s et 0s qui indiquent respectivement les valeurs High et Low.

Avantages de la communication numérique
Au fur et à mesure que les signaux sont numérisés, la communication numérique présente de nombreux avantages par rapport à la communication analogique, tels que:
L'effet de la distorsion, du bruit et des interférences est bien moindre dans les signaux numériques car ils sont moins affectés.
Les circuits numériques sont plus fiables.
Les circuits numériques sont faciles à concevoir et moins chers que les circuits analogiques.
L'implémentation matérielle dans les circuits numériques est plus flexible que l'analogique.
L'apparition de diaphonie est très rare dans la communication numérique.
Le signal n'est pas modifié car l'impulsion a besoin d'une forte perturbation pour modifier ses propriétés, ce qui est très difficile.
Des fonctions de traitement du signal telles que le cryptage et la compression sont utilisées dans les circuits numériques pour maintenir le secret des informations.
La probabilité d'occurrence d'erreur est réduite en utilisant des codes de détection et de correction d'erreur.
La technique du spectre étalé est utilisée pour éviter le brouillage du signal.
La combinaison de signaux numériques à l'aide du multiplexage par répartition dans le temps (TDM) est plus facile que la combinaison de signaux analogiques à l'aide du multiplexage par répartition en fréquence (FDM).
Le processus de configuration des signaux numériques est plus simple que celui des signaux analogiques.
Les signaux numériques peuvent être enregistrés et récupérés plus facilement que les signaux analogiques.
De nombreux circuits numériques ont des techniques de codage presque communes et, par conséquent, des dispositifs similaires peuvent être utilisés à plusieurs fins.
La capacité du canal est effectivement utilisée par les signaux numériques.
Éléments de la communication numérique
Les éléments qui forment un système de communication numérique sont représentés par le schéma fonctionnel suivant pour faciliter la compréhension.
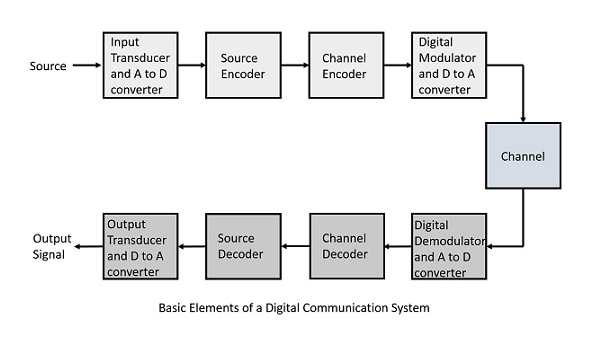
Voici les sections du système de communication numérique.
La source
La source peut être un analog signal. Example: Un signal sonore
Transducteur d'entrée
Il s'agit d'un transducteur qui prend une entrée physique et la convertit en un signal électrique (Example: microphone). Ce bloc se compose également d'unanalog to digital convertisseur où un signal numérique est nécessaire pour d'autres processus.
Un signal numérique est généralement représenté par une séquence binaire.
Encodeur source
L'encodeur source compresse les données en un nombre minimum de bits. Ce processus contribue à une utilisation efficace de la bande passante. Il supprime les bits redondants (bits en excès inutiles, c'est-à-dire zéros).
Encodeur de canal
L'encodeur de canal effectue le codage pour la correction d'erreur. Pendant la transmission du signal, en raison du bruit dans le canal, le signal peut être altéré et donc pour éviter cela, le codeur de canal ajoute des bits redondants aux données transmises. Ce sont les bits de correction d'erreur.
Modulateur numérique
Le signal à transmettre est ici modulé par une porteuse. Le signal est également converti en analogique à partir de la séquence numérique, afin de le faire voyager à travers le canal ou le support.
Canal
Le canal ou un support permet au signal analogique de transmettre de l'extrémité de l'émetteur à l'extrémité du récepteur.
Démodulateur numérique
C'est la première étape du côté du récepteur. Le signal reçu est démodulé et reconverti de l'analogique au numérique. Le signal est reconstruit ici.
Décodeur de canal
Le décodeur de canal, après avoir détecté la séquence, effectue quelques corrections d'erreurs. Les distorsions qui pourraient survenir lors de la transmission, sont corrigées par l'ajout de quelques bits redondants. Cet ajout de bits aide à la récupération complète du signal d'origine.
Décodeur source
Le signal résultant est à nouveau numérisé par échantillonnage et quantification de sorte que la sortie numérique pure soit obtenue sans perte d'informations. Le décodeur source recrée la sortie source.
Transducteur de sortie
C'est le dernier bloc qui convertit le signal dans la forme physique d'origine, qui était à l'entrée de l'émetteur. Il convertit le signal électrique en sortie physique (Example: haut-parleur).
Signal de sortie
C'est la sortie qui est produite après tout le processus. Example - Le signal sonore reçu.
Cette unité a traité de l'introduction, de la numérisation des signaux, des avantages et des éléments des communications numériques. Dans les prochains chapitres, nous apprendrons en détail les concepts de communication numérique.
Modulation est le processus de variation d'un ou de plusieurs paramètres d'un signal de porteuse en fonction des valeurs instantanées du signal de message.
Le signal de message est le signal qui est transmis pour la communication et le signal de porteuse est un signal haute fréquence qui n'a pas de données, mais qui est utilisé pour une transmission longue distance.
Il existe de nombreuses techniques de modulation, classées selon le type de modulation utilisé. Parmi eux tous, la technique de modulation numérique utilisée estPulse Code Modulation (PCM).
Un signal est modulé par impulsions pour convertir ses informations analogiques en une séquence binaire, c'est-à-dire 1s et 0s. La sortie d'un PCM ressemblera à une séquence binaire. La figure suivante montre un exemple de sortie PCM par rapport aux valeurs instantanées d'une onde sinusoïdale donnée.
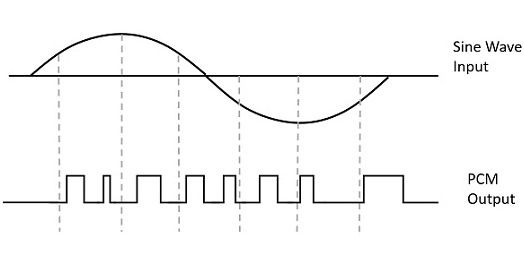
Au lieu d'un train d'impulsions, PCM produit une série de nombres ou de chiffres, et par conséquent ce processus est appelé comme digital. Chacun de ces chiffres, bien qu'en code binaire, représente l'amplitude approximative de l'échantillon de signal à cet instant.
Dans la modulation par code d'impulsion, le signal de message est représenté par une séquence d'impulsions codées. Ce signal de message est obtenu en représentant le signal sous forme discrète à la fois en temps et en amplitude.
Éléments de base du PCM
La section émetteur d'un circuit modulateur à code d'impulsion se compose de Sampling, Quantizing et Encoding, qui sont exécutées dans la section de conversion analogique-numérique. Le filtre passe-bas avant l'échantillonnage empêche l'aliasing du signal de message.
Les opérations de base dans la section récepteur sont regeneration of impaired signals, decoding, et reconstructiondu train d'impulsions quantifié. Voici le schéma de principe du PCM qui représente les éléments de base des sections émetteur et récepteur.
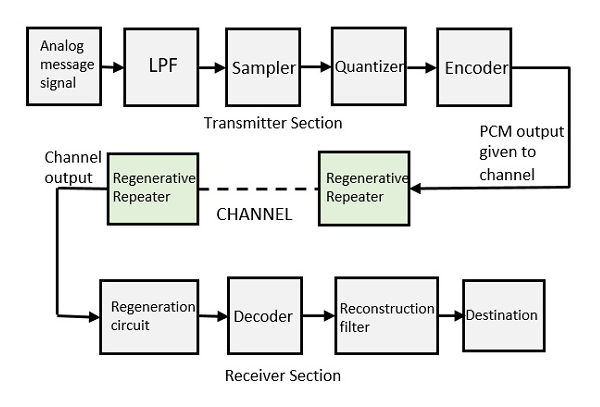
Filtre passe bas
Ce filtre élimine les composantes haute fréquence présentes dans le signal analogique d'entrée qui sont supérieures à la fréquence la plus élevée du signal de message, pour éviter le crénelage du signal de message.
Échantillonneur
C'est la technique qui permet de collecter les données d'échantillon à des valeurs instantanées du signal de message, de manière à reconstruire le signal d'origine. La fréquence d'échantillonnage doit être supérieure à deux fois la composante de fréquence la plus élevéeW du signal de message, conformément au théorème d'échantillonnage.
Quantificateur
La quantification est un processus de réduction des bits excessifs et de confinement des données. La sortie échantillonnée lorsqu'elle est fournie au quantificateur, réduit les bits redondants et compresse la valeur.
Encodeur
La numérisation du signal analogique est effectuée par le codeur. Il désigne chaque niveau quantifié par un code binaire. L'échantillonnage effectué ici est le processus d'échantillonnage et de conservation. Ces trois sections (LPF, Sampler et Quantizer) agiront comme un convertisseur analogique-numérique. Le codage minimise la bande passante utilisée.
Répéteur régénératif
Cette section augmente la force du signal. La sortie du canal a également un circuit répéteur régénératif, pour compenser la perte de signal et reconstruire le signal, et également pour augmenter sa force.
Décodeur
Le circuit décodeur décode la forme d'onde codée par impulsions pour reproduire le signal d'origine. Ce circuit fait office de démodulateur.
Filtre de reconstruction
Une fois la conversion numérique-analogique effectuée par le circuit régénératif et le décodeur, un filtre passe-bas est utilisé, appelé filtre de reconstruction pour récupérer le signal d'origine.
Par conséquent, le circuit du modulateur de code d'impulsion numérise le signal analogique donné, le code et l'échantillonne, puis le transmet sous une forme analogique. L'ensemble de ce processus est répété dans un motif inverse pour obtenir le signal d'origine.
Sampling est défini comme: «Le processus de mesure des valeurs instantanées d'un signal en temps continu sous une forme discrète.»
Sample est une donnée extraite de l'ensemble des données qui est continue dans le domaine temporel.
Lorsqu'une source génère un signal analogique et si celui-ci doit être numérisé, avoir 1s et 0sc'est-à-dire, haut ou bas, le signal doit être discrétisé dans le temps. Cette discrétisation du signal analogique est appelée échantillonnage.
La figure suivante indique un signal continu x (t) et un signal échantillonné xs (t). Quandx (t) est multiplié par un train d'impulsions périodique, le signal échantillonné xs (t) Est obtenu.
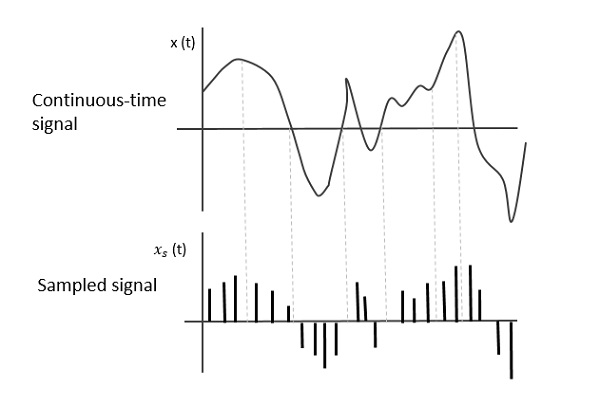
Taux d'échantillonnage
Pour discrétiser les signaux, l'écart entre les échantillons doit être corrigé. Cet écart peut être qualifié desampling period Ts.
$$ Échantillonnage \: Frequency = \ frac {1} {T_ {s}} = f_s $$
Où,
$ T_s $ est le temps d'échantillonnage
$ f_s $ est la fréquence d'échantillonnage ou le taux d'échantillonnage
Sampling frequencyest l'inverse de la période d'échantillonnage. Cette fréquence d'échantillonnage peut être simplement appeléeSampling rate. La fréquence d'échantillonnage indique le nombre d'échantillons prélevés par seconde, ou pour un ensemble fini de valeurs.
Pour qu'un signal analogique soit reconstruit à partir du signal numérisé, la fréquence d'échantillonnage doit être fortement prise en compte. Le taux d'échantillonnage doit être tel que les données du signal de message ne doivent pas être perdues ni se chevaucher. Par conséquent, un taux a été fixé pour cela, appelé taux de Nyquist.
Taux Nyquist
Supposons qu'un signal soit limité en bande sans composantes de fréquence supérieures à WHertz. Cela signifie,West la fréquence la plus élevée. Pour un tel signal, pour une reproduction efficace du signal original, la fréquence d'échantillonnage doit être deux fois la fréquence la plus élevée.
Ce qui signifie,
$$ f_S = 2W $$
Où,
$ f_S $ est le taux d'échantillonnage
W est la fréquence la plus élevée
Ce taux d'échantillonnage est appelé Nyquist rate.
Un théorème appelé, Théorème d'échantillonnage, a été énoncé sur la théorie de ce taux de Nyquist.
Théorème d'échantillonnage
Le théorème d'échantillonnage, également appelé Nyquist theorem, fournit la théorie d'une fréquence d'échantillonnage suffisante en termes de bande passante pour la classe de fonctions à bande limitée.
Le théorème d'échantillonnage stipule qu '«un signal peut être reproduit exactement s'il est échantillonné à la fréquence fs qui est supérieure à deux fois la fréquence maximale W. »
Pour comprendre ce théorème d'échantillonnage, considérons un signal à bande limitée, c'est-à-dire un signal dont la valeur est non-zero entre certains –W et W Hertz.
Un tel signal est représenté par $ x (f) = 0 \: pour \: \ mid f \ mid> W $
Pour le signal à temps continu x (t), le signal à bande limitée dans le domaine fréquentiel, peut être représenté comme illustré dans la figure suivante.
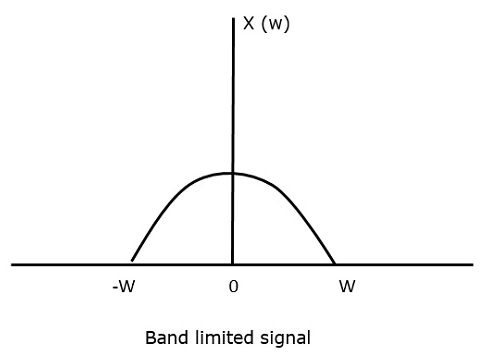
Nous avons besoin d'une fréquence d'échantillonnage, une fréquence à laquelle il ne devrait y avoir aucune perte d'information, même après échantillonnage. Pour cela, nous avons le taux de Nyquist selon lequel la fréquence d'échantillonnage doit être deux fois la fréquence maximale. C'est le taux critique d'échantillonnage.
Si le signal x(t) est échantillonné au-dessus du taux de Nyquist, le signal d'origine peut être récupéré, et s'il est échantillonné au-dessous du taux de Nyquist, le signal ne peut pas être récupéré.
La figure suivante explique un signal, s'il est échantillonné à une fréquence supérieure à 2w dans le domaine fréquentiel.
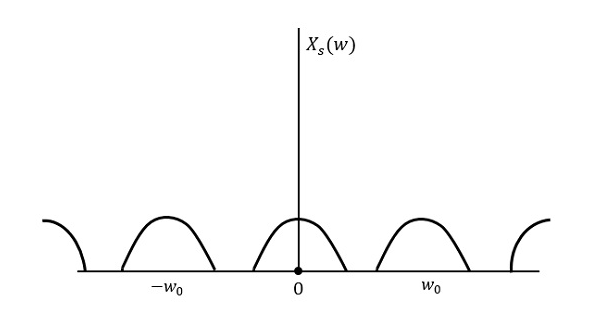
La figure ci-dessus montre la transformée de Fourier d'un signal xs (t). Ici, les informations sont reproduites sans aucune perte. Il n'y a pas de mélange et donc la récupération est possible.
La transformée de Fourier du signal xs (t) est
$$ X_s (w) = \ frac {1} {T_ {s}} \ sum_ {n = - \ infty} ^ \ infty X (w-nw_0) $$
Où $ T_s $ = Sampling Period et $ w_0 = \ frac {2 \ pi} {T_s} $
Voyons ce qui se passe si le taux d'échantillonnage est égal à deux fois la fréquence la plus élevée (2W)
Cela signifie,
$$ f_s = 2W $$
Où,
$ f_s $ est la fréquence d'échantillonnage
W est la fréquence la plus élevée
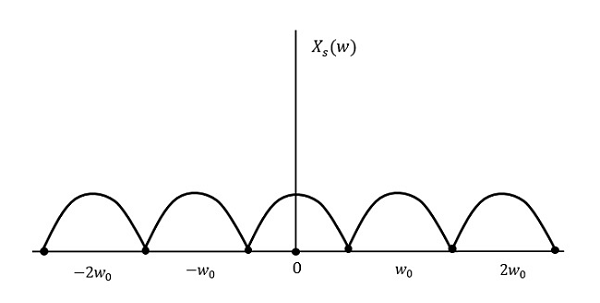
Le résultat sera comme indiqué dans la figure ci-dessus. Les informations sont remplacées sans aucune perte. C'est donc aussi un bon taux d'échantillonnage.
Maintenant, regardons la condition,
$$ f_s <2W $$
Le motif résultant ressemblera à la figure suivante.

Nous pouvons observer à partir du schéma ci-dessus que le chevauchement d'informations est effectué, ce qui conduit à un mélange et à une perte d'informations. Ce phénomène indésirable de chevauchement est appelé aliasing.
Aliasing
Le crénelage peut être appelé «le phénomène d'une composante haute fréquence dans le spectre d'un signal, prenant l'identité d'une composante basse fréquence dans le spectre de sa version échantillonnée».
Les mesures correctives prises pour réduire l'effet de l'aliasing sont:
Dans la section émetteur du PCM, un low pass anti-aliasing filter est utilisé, avant l'échantillonneur, pour éliminer les composantes haute fréquence, qui sont indésirables.
Le signal qui est échantillonné après filtrage, est échantillonné à un taux légèrement supérieur au taux de Nyquist.
Ce choix d'avoir le taux d'échantillonnage plus élevé que le taux de Nyquist, contribue également à la conception plus facile du reconstruction filter au récepteur.
Portée de la transformée de Fourier
On observe généralement que, nous cherchons l'aide des séries de Fourier et des transformées de Fourier dans l'analyse des signaux et aussi dans la démonstration des théorèmes. C'est parce que -
La transformée de Fourier est l'extension de la série de Fourier pour les signaux non périodiques.
La transformée de Fourier est un outil mathématique puissant qui aide à visualiser les signaux dans différents domaines et aide à analyser les signaux facilement.
Tout signal peut être décomposé en termes de somme des sinus et cosinus en utilisant cette transformée de Fourier.
Dans le chapitre suivant, discutons du concept de quantification.
La numérisation des signaux analogiques implique l'arrondissement des valeurs qui sont approximativement égales aux valeurs analogiques. La méthode d'échantillonnage choisit quelques points sur le signal analogique, puis ces points sont joints pour arrondir la valeur à une valeur presque stabilisée. Un tel processus est appelé commeQuantization.
Quantification d'un signal analogique
Les convertisseurs analogique-numérique exécutent ce type de fonction pour créer une série de valeurs numériques à partir du signal analogique donné. La figure suivante représente un signal analogique. Ce signal pour être converti en numérique, doit subir un échantillonnage et une quantification.
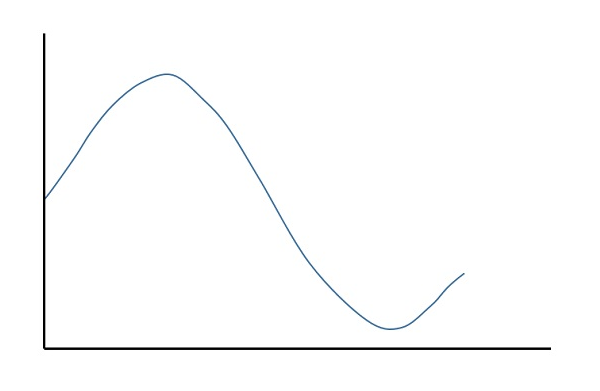
La quantification d'un signal analogique se fait en discrétisant le signal avec un certain nombre de niveaux de quantification. Quantization représente les valeurs échantillonnées de l'amplitude par un ensemble fini de niveaux, ce qui signifie convertir un échantillon d'amplitude continue en un signal à temps discret.
La figure suivante montre comment un signal analogique est quantifié. La ligne bleue représente le signal analogique tandis que la brune représente le signal quantifié.
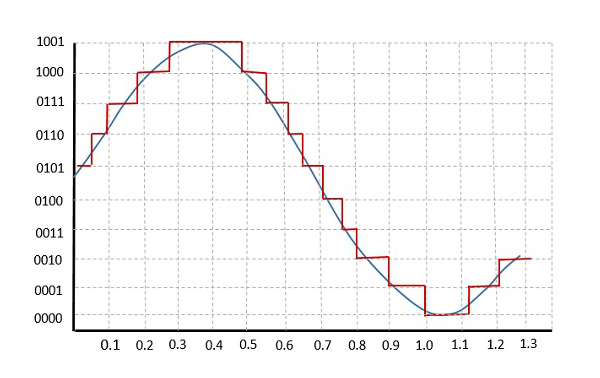
L'échantillonnage et la quantification entraînent une perte d'informations. La qualité de la sortie d'un quantificateur dépend du nombre de niveaux de quantification utilisés. Les amplitudes discrètes de la sortie quantifiée sont appelées commerepresentation levels ou reconstruction levels. L'espacement entre les deux niveaux de représentation adjacents est appelé unquantum ou step-size.
La figure suivante montre le signal quantifié résultant qui est la forme numérique du signal analogique donné.
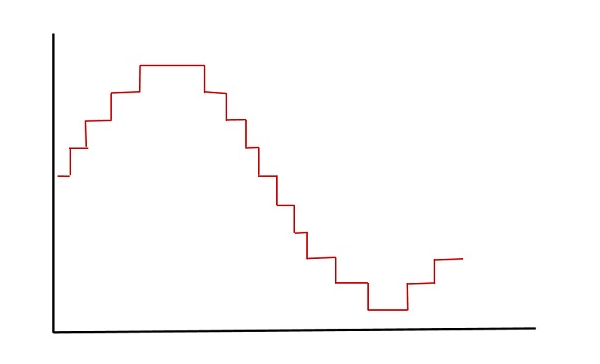
Ceci est également appelé comme Stair-case forme d'onde, en fonction de sa forme.
Types de quantification
Il existe deux types de quantification: la quantification uniforme et la quantification non uniforme.
Le type de quantification dans lequel les niveaux de quantification sont uniformément espacés est appelé Uniform Quantization. Le type de quantification dans lequel les niveaux de quantification sont inégaux et la plupart du temps la relation entre eux est logarithmique, est appeléNon-uniform Quantization.
Il existe deux types de quantification uniforme. Ils sont de type Mid-Rise et Mid-Tread. Les figures suivantes représentent les deux types de quantification uniforme.
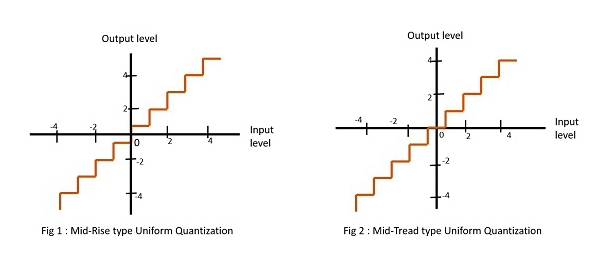
La figure 1 montre le type à mi-hauteur et la figure 2 montre le type à mi-bande de roulement de quantification uniforme.
le Mid-Risele type est ainsi appelé parce que l'origine se trouve au milieu d'une partie en élévation du graphe en forme d'escalier. Les niveaux de quantification de ce type sont en nombre pair.
le Mid-treadle type est ainsi appelé parce que l'origine se trouve au milieu d'une bande de roulement du graphe en forme d'escalier. Les niveaux de quantification de ce type sont en nombre impair.
Les quantificateurs uniformes de type mi-hauteur et mi-bande de roulement sont symétriques par rapport à l'origine.
Erreur de quantification
Pour tout système, pendant son fonctionnement, il y a toujours une différence dans les valeurs de son entrée et de sa sortie. Le traitement du système entraîne une erreur, qui correspond à la différence de ces valeurs.
La différence entre une valeur d'entrée et sa valeur quantifiée est appelée Quantization Error. UNEQuantizerest une fonction logarithmique qui effectue la quantification (arrondissant la valeur). Un convertisseur analogique-numérique (ADC) fonctionne comme un quantificateur.
La figure suivante illustre un exemple d'erreur de quantification, indiquant la différence entre le signal d'origine et le signal quantifié.
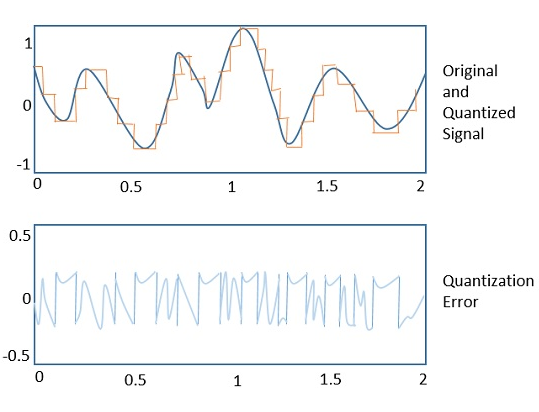
Bruit de quantification
Il s'agit d'un type d'erreur de quantification, qui se produit généralement dans le signal audio analogique, tout en le quantifiant en numérique. Par exemple, dans la musique, les signaux changent continuellement, là où une régularité n'est pas trouvée dans les erreurs. De telles erreurs créent un bruit à large bande appeléQuantization Noise.
Companding dans PCM
Le mot Compandingest une combinaison de compression et d'expansion, ce qui signifie qu'il fait les deux. Il s'agit d'une technique non linéaire utilisée dans le PCM qui compresse les données au niveau de l'émetteur et étend les mêmes données au récepteur. Les effets du bruit et de la diaphonie sont réduits en utilisant cette technique.
Il existe deux types de techniques de compression. Ils sont -
Technique de compression A-law
Une quantification uniforme est obtenue à A = 1, où la courbe caractéristique est linéaire et aucune compression n'est effectuée.
A-law a mi-hauteur à l'origine. Par conséquent, il contient une valeur non nulle.
La compression A-law est utilisée pour les systèmes téléphoniques PCM.
Technique de compression µ-law
Une quantification uniforme est obtenue à µ = 0, où la courbe caractéristique est linéaire et aucune compression n'est effectuée.
µ-law a la mi-bande de roulement à l'origine. Par conséquent, il contient une valeur nulle.
La compression de la loi µ est utilisée pour les signaux vocaux et musicaux.
La loi µ est utilisée en Amérique du Nord et au Japon.
Pour les échantillons qui sont fortement corrélés, lorsqu'ils sont codés par la technique PCM, laissez les informations redondantes derrière. Pour traiter ces informations redondantes et obtenir une meilleure sortie, il est sage de prendre une valeur échantillonnée prédite, supposée à partir de sa sortie précédente et de les résumer avec les valeurs quantifiées. Un tel processus est appelé commeDifferential PCM (DPCM) technique.
Émetteur DPCM
L'émetteur DPCM se compose d'un quantificateur et d'un prédicteur avec deux circuits d'été. Voici le schéma de principe de l'émetteur DPCM.

Les signaux à chaque point sont nommés comme -
$ x (nT_s) $ est l'entrée échantillonnée
$ \ widehat {x} (nT_s) $ est l'échantillon prédit
$ e (nT_s) $ est la différence entre l'entrée échantillonnée et la sortie prédite, souvent appelée erreur de prédiction
$ v (nT_s) $ est la sortie quantifiée
$ u (nT_s) $ est l'entrée du prédicteur qui est en fait la sortie additionnelle de la sortie du prédicteur et de la sortie du quantificateur
Le prédicteur produit les échantillons supposés à partir des sorties précédentes du circuit émetteur. L'entrée de ce prédicteur est la version quantifiée du signal d'entrée $ x (nT_s) $.
La sortie du quantificateur est représentée par -
$$ v (nT_s) = Q [e (nT_s)] $$
$ = e (nT_s) + q (nT_s) $
Où q (nTs) est l'erreur de quantification
L'entrée du prédicteur est la somme de la sortie du quantificateur et de la sortie du prédicteur,
$$ u (nT_s) = \ widehat {x} (nT_s) + v (nT_s) $$
$ u (nT_s) = \ widehat {x} (nT_s) + e (nT_s) + q (nT_s) $
$$ u (nT_s) = x (nT_s) + q (nT_s) $$
Le même circuit prédicteur est utilisé dans le décodeur pour reconstruire l'entrée d'origine.
Récepteur DPCM
Le schéma de principe du récepteur DPCM se compose d'un décodeur, d'un prédicteur et d'un circuit d'été. Voici le schéma du récepteur DPCM.

La notation des signaux est la même que les précédentes. En l'absence de bruit, l'entrée du récepteur codée sera la même que la sortie de l'émetteur codée.
Comme mentionné précédemment, le prédicteur suppose une valeur, basée sur les sorties précédentes. L'entrée donnée au décodeur est traitée et cette sortie est additionnée à la sortie du prédicteur, pour obtenir une meilleure sortie.
La fréquence d'échantillonnage d'un signal doit être supérieure à la fréquence de Nyquist, pour obtenir un meilleur échantillonnage. Si cet intervalle d'échantillonnage en PCM différentiel est considérablement réduit, la différence d'amplitude échantillon-échantillon est très petite, comme si la différence était1-bit quantization, alors la taille du pas sera très petite, c'est-à-dire, Δ (delta).
Modulation Delta
Le type de modulation, où la fréquence d'échantillonnage est beaucoup plus élevée et dans laquelle le pas après quantification est d'une valeur plus petite Δ, une telle modulation est appelée delta modulation.
Caractéristiques de la modulation delta
Voici quelques-unes des caractéristiques de la modulation delta.
Une entrée suréchantillonnée est utilisée pour utiliser pleinement la corrélation de signal.
La conception de la quantification est simple.
La séquence d'entrée est beaucoup plus élevée que le taux de Nyquist.
La qualité est modérée.
La conception du modulateur et du démodulateur est simple.
L'approximation en escalier de la forme d'onde de sortie.
La taille du pas est très petite, c'est-à-dire Δ (delta).
Le débit binaire peut être décidé par l'utilisateur.
Cela implique une mise en œuvre plus simple.
La modulation Delta est une forme simplifiée de la technique DPCM, également considérée comme 1-bit DPCM scheme. Lorsque l'intervalle d'échantillonnage est réduit, la corrélation du signal sera plus élevée.
Modulateur Delta
Le Delta Modulator comprend un quantificateur 1 bit et un circuit de retard ainsi que deux circuits d'été. Voici le schéma de principe d'un modulateur delta.
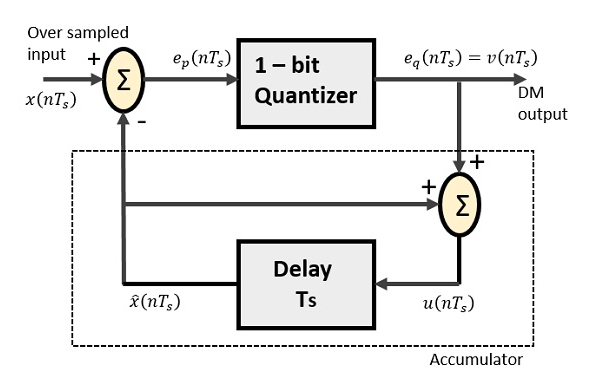
Le circuit prédicteur en DPCM est remplacé par un simple circuit à retard en DM.
À partir du diagramme ci-dessus, nous avons les notations comme -
$ x (nT_s) $ = sur l'entrée échantillonnée
$ e_p (nT_s) $ = sortie d'été et entrée de quantificateur
$ e_q (nT_s) $ = sortie du quantificateur = $ v (nT_s) $
$ \ widehat {x} (nT_s) $ = sortie du circuit de retard
$ u (nT_s) $ = entrée du circuit de retard
En utilisant ces notations, nous allons maintenant essayer de comprendre le processus de modulation delta.
$ e_p (nT_s) = x (nT_s) - \ widehat {x} (nT_s) $
--------- équation 1
$ = x (nT_s) - u ([n - 1] T_s) $
$ = x (nT_s) - [\ widehat {x} [[n - 1] T_s] + v [[n-1] T_s]] $
--------- équation 2
Plus loin,
$ v (nT_s) = e_q (nT_s) = S.sig. [e_p (nT_s)] $
--------- équation 3
$ u (nT_s) = \ widehat {x} (nT_s) + e_q (nT_s) $
Où,
$ \ widehat {x} (nT_s) $ = la valeur précédente du circuit de retard
$ e_q (nT_s) $ = sortie du quantificateur = $ v (nT_s) $
Par conséquent,
$ u (nT_s) = u ([n-1] T_s) + v (nT_s) $
--------- équation 4
Ce qui signifie,
The present input of the delay unit
= (The previous output of the delay unit) + (the present quantizer output)
En supposant une condition d'accumulation nulle,
$ u (nT_s) = S \ Displaystyle \ sum \ limits_ {j = 1} ^ n sig [e_p (jT_s)] $
Accumulated version of DM output = $ \ Displaystyle \ sum \ limits_ {j = 1} ^ nv (jT_s) $
--------- équation 5
Maintenant, notez que
$ \ widehat {x} (nT_s) = u ([n-1] T_s) $
$ = \ Displaystyle \ somme \ limites_ {j = 1} ^ {n - 1} v (jT_s) $
--------- équation 6
La sortie de l'unité de retard est une sortie de l'accumulateur retardée d'un échantillon.
À partir des équations 5 et 6, nous obtenons une structure possible pour le démodulateur.
Une forme d'onde approximative de cas d'escalier sera la sortie du modulateur delta avec la taille de pas comme delta (Δ). La qualité de sortie de la forme d'onde est moyenne.
Démodulateur Delta
Le démodulateur delta comprend un filtre passe-bas, un sommateur et un circuit de retard. Le circuit de prédiction est ici éliminé et par conséquent aucune entrée supposée n'est donnée au démodulateur.
Voici le diagramme du démodulateur delta.
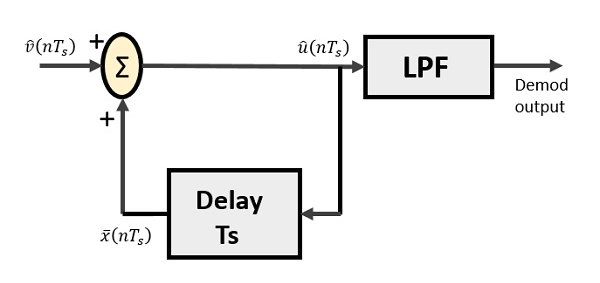
À partir du diagramme ci-dessus, nous avons les notations comme -
$ \ widehat {v} (nT_s) $ est l'exemple d'entrée
$ \ widehat {u} (nT_s) $ est la sortie d'été
$ \ bar {x} (nT_s) $ est la sortie retardée
Une séquence binaire sera donnée en entrée du démodulateur. La sortie approximative de la cage d'escalier est donnée au LPF.
Le filtre passe-bas est utilisé pour de nombreuses raisons, mais la principale raison est l'élimination du bruit pour les signaux hors bande. L'erreur de taille de pas qui peut survenir au niveau de l'émetteur est appeléegranular noise, qui est éliminé ici. S'il n'y a pas de bruit, la sortie du modulateur est égale à l'entrée du démodulateur.
Avantages de DM sur DPCM
Quantificateur 1 bit
Conception très simple du modulateur et du démodulateur
Cependant, il existe un peu de bruit dans DM.
Pente Distorsion de surcharge (quand Δ est petite)
Bruit granulaire (quand Δ est large)
Modulation adaptative delta (ADM)
Dans la modulation numérique, nous avons rencontré un certain problème de détermination de la taille du pas, qui influence la qualité de l'onde de sortie.
Un pas plus grand est nécessaire dans la pente raide du signal de modulation et un pas plus petit est nécessaire là où le message a une petite pente. Les moindres détails sont manqués dans le processus. Ainsi, il serait préférable que nous puissions contrôler l'ajustement de la taille de pas, en fonction de nos besoins afin d'obtenir l'échantillonnage de la manière souhaitée. C'est le concept deAdaptive Delta Modulation.
Voici le schéma de principe du modulateur delta adaptatif.
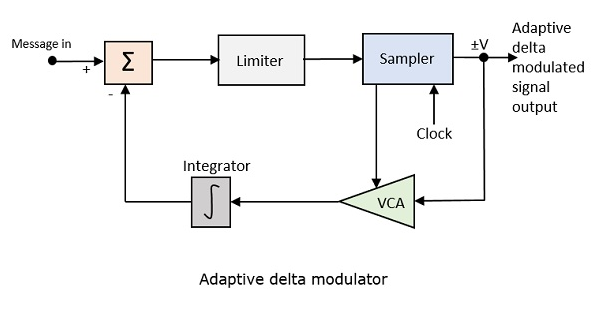
Le gain de l'amplificateur commandé en tension est ajusté par le signal de sortie de l'échantillonneur. Le gain de l'amplificateur détermine la taille du pas et les deux sont proportionnels.
ADM quantifie la différence entre la valeur de l'échantillon actuel et la valeur prédite de l'échantillon suivant. Il utilise une hauteur de pas variable pour prédire les valeurs suivantes, pour la reproduction fidèle des valeurs à variation rapide.
Il existe quelques techniques qui ont ouvert la voie aux processus de communication numérique. Pour que les signaux soient numérisés, nous avons les techniques d'échantillonnage et de quantification.
Pour qu'ils soient représentés mathématiquement, nous disposons de techniques LPC et de multiplexage numérique. Ces techniques de modulation numérique sont discutées plus en détail.
Codage prédictif linéaire
Linear Predictive Coding (LPC)est un outil qui représente les signaux vocaux numériques dans un modèle prédictif linéaire. Ceci est principalement utilisé dans le traitement du signal audio, la synthèse vocale, la reconnaissance vocale, etc.
La prédiction linéaire est basée sur l'idée que l'échantillon actuel est basé sur la combinaison linéaire d'échantillons passés. L'analyse estime les valeurs d'un signal à temps discret comme une fonction linéaire des échantillons précédents.
L'enveloppe spectrale est représentée sous une forme compressée, en utilisant les informations du modèle prédictif linéaire. Cela peut être représenté mathématiquement par -
$ s (n) = \ Displaystyle \ sum \ limits_ {k = 1} ^ p \ alpha_k s (n - k) $ pour une valeur de p et αk
Où
s(n) est l'échantillon de discours actuel
k est un échantillon particulier
p est la valeur la plus récente
αk est le coefficient prédictif
s(n - k) est l'exemple de discours précédent
Pour LPC, les valeurs du coefficient de prédiction sont déterminées en minimisant la somme des différences au carré (sur un intervalle fini) entre les échantillons de parole réels et ceux qui sont prédits linéairement.
C'est une méthode très utile pour encoding speechà un débit binaire faible. La méthode LPC est très proche de laFast Fourier Transform (FFT) méthode.
Multiplexage
Multiplexingest le processus de combinaison de plusieurs signaux en un seul signal, sur un support partagé. Ces signaux, s'ils sont de nature analogique, le processus est appeléanalog multiplexing. Si les signaux numériques sont multiplexés, il est appelédigital multiplexing.
Le multiplexage a d'abord été développé dans la téléphonie. Un certain nombre de signaux ont été combinés pour être envoyés via un seul câble. Le processus de multiplexage divise un canal de communication en plusieurs nombres de canaux logiques, attribuant chacun à un signal de message différent ou à un flux de données à transférer. L'appareil qui effectue le multiplexage peut être appeléMUX. Le processus inverse, c'est-à-dire l'extraction du nombre de canaux à partir d'un seul, qui est effectué au niveau du récepteur est appelé commede-multiplexing. L'appareil qui effectue le démultiplexage est appeléDEMUX.
Les figures suivantes représentent MUX et DEMUX. Leur utilisation principale est dans le domaine des communications.
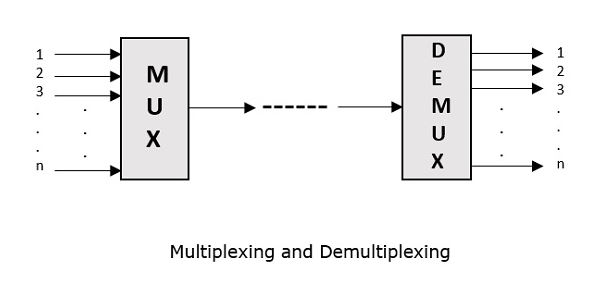
Types de multiplexeurs
Il existe principalement deux types de multiplexeurs, à savoir analogique et numérique. Ils sont ensuite divisés en FDM, WDM et TDM. La figure suivante donne une idée détaillée de cette classification.
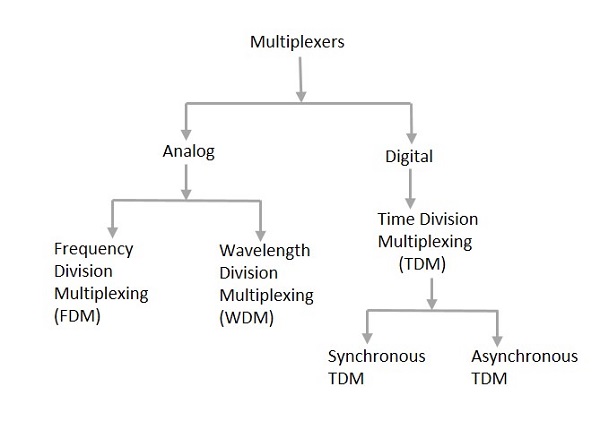
En fait, il existe de nombreux types de techniques de multiplexage. De tous, nous avons les principaux types avec classification générale, mentionnés dans la figure ci-dessus.
Multiplexage analogique
Les techniques de multiplexage analogique impliquent des signaux de nature analogique. Les signaux analogiques sont multiplexés en fonction de leur fréquence (FDM) ou de leur longueur d'onde (WDM).
Multiplexage par répartition en fréquence (FDM)
En multiplexage analogique, la technique la plus utilisée est Frequency Division Multiplexing (FDM). Cette technique utilise différentes fréquences pour combiner des flux de données, pour les envoyer sur un support de communication, en un seul signal.
Example - Un émetteur de télévision traditionnel, qui envoie plusieurs chaînes via un seul câble, utilise FDM.
Multiplexage par division de longueur d'onde (WDM)
Le multiplexage par division de longueur d'onde est une technique analogique, dans laquelle de nombreux flux de données de différentes longueurs d'onde sont transmis dans le spectre lumineux. Si la longueur d'onde augmente, la fréquence du signal diminue. UNEprism qui peut transformer différentes longueurs d'onde en une seule ligne, peut être utilisé à la sortie de MUX et à l'entrée de DEMUX.
Example - Les communications par fibre optique utilisent la technique WDM pour fusionner différentes longueurs d'onde en une seule lumière pour la communication.
Multiplexage numérique
Le terme numérique représente les bits d'information discrets. Par conséquent, les données disponibles se présentent sous la forme de trames ou de paquets, qui sont discrets.
Multiplexage par répartition dans le temps (TDM)
Dans TDM, le délai est divisé en créneaux. Cette technique permet de transmettre un signal sur un seul canal de communication, en allouant un créneau pour chaque message.
De tous les types de TDM, les principaux sont TDM synchrone et asynchrone.
TDM synchrone
En TDM synchrone, l'entrée est connectée à une trame. S'il y a 'n'nombre de connexions, puis le cadre est divisé en'n' tranches de temps. Un emplacement est alloué pour chaque ligne d'entrée.
Dans cette technique, la fréquence d'échantillonnage est commune à tous les signaux et, par conséquent, la même entrée d'horloge est donnée. Le MUX alloue à tout moment le même emplacement à chaque appareil.
TDM asynchrone
Dans le TDM asynchrone, la fréquence d'échantillonnage est différente pour chacun des signaux et une horloge commune n'est pas nécessaire. Si le périphérique alloué, pour un créneau horaire, ne transmet rien et reste inactif, alors ce créneau est attribué à un autre dispositif, contrairement à la synchronisation. Ce type de TDM est utilisé dans les réseaux en mode de transfert asynchrone.
Répéteur régénératif
Pour qu'un système de communication soit fiable, il doit transmettre et recevoir les signaux efficacement, sans aucune perte. Une onde PCM, après avoir été transmise à travers un canal, est déformée en raison du bruit introduit par le canal.
L'impulsion régénérative comparée à l'impulsion d'origine et à l'impulsion reçue sera comme illustré dans la figure suivante.

Pour une meilleure reproduction du signal, un circuit appelé regenerative repeaterest utilisé dans le chemin avant le récepteur. Cela aide à restaurer les signaux des pertes survenues. Voici la représentation schématique.
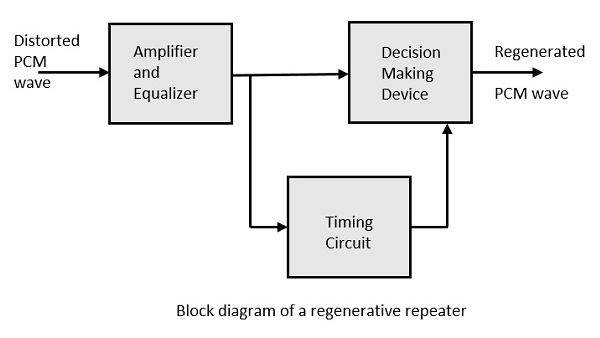
Il se compose d'un égaliseur avec un amplificateur, un circuit de synchronisation et un dispositif de prise de décision. Leur fonctionnement de chacun des composants est détaillé comme suit.
Égaliseur
Le canal produit des distorsions d'amplitude et de phase des signaux. Cela est dû aux caractéristiques de transmission du canal. Le circuit égaliseur compense ces pertes en façonnant les impulsions reçues.
Circuit de chronométrage
Pour obtenir une sortie de qualité, l'échantillonnage des impulsions doit être effectué là où le rapport signal sur bruit (SNR) est maximal. Pour réaliser cet échantillonnage parfait, un train d'impulsions périodique doit être dérivé des impulsions reçues, ce qui est fait par le circuit de synchronisation.
Par conséquent, le circuit de synchronisation alloue l'intervalle de synchronisation pour l'échantillonnage à un SNR élevé, à travers les impulsions reçues.
Dispositif de décision
Le circuit de synchronisation détermine les temps d'échantillonnage. Le dispositif de décision est activé à ces moments d'échantillonnage. Le dispositif de décision décide de sa sortie en fonction du fait que l'amplitude de l'impulsion quantifiée et du bruit dépasse une valeur prédéterminée ou non.
Ce ne sont là que quelques-unes des techniques utilisées dans les communications numériques. Il existe d'autres techniques importantes à apprendre, appelées techniques de codage de données. Découvrons-les dans les chapitres suivants, après avoir examiné les codes de ligne.
UNE line codeest le code utilisé pour la transmission de données d'un signal numérique sur une ligne de transmission. Ce processus de codage est choisi de manière à éviter le chevauchement et la distorsion du signal comme les interférences entre symboles.
Propriétés du codage de ligne
Voici les propriétés du codage de ligne -
Comme le codage est fait pour faire transmettre plus de bits sur un seul signal, la bande passante utilisée est beaucoup plus réduite.
Pour une bande passante donnée, la puissance est utilisée efficacement.
La probabilité d'erreur est très réduite.
La détection d'erreur est effectuée et le bipolaire dispose également d'une capacité de correction.
La densité de puissance est très favorable.
Le contenu de la synchronisation est adéquat.
Longues chaînes de 1s et 0s est évité pour maintenir la transparence.
Types de codage de ligne
Il existe 3 types de codage de ligne
- Unipolar
- Polar
- Bi-polar
Signalisation unipolaire
La signalisation unipolaire est également appelée On-Off Keying ou simplement OOK.
La présence d'impulsion représente un 1 et l'absence d'impulsion représente un 0.
Il existe deux variantes de la signalisation unipolaire -
- Non retour à zéro (NRZ)
- Retour à zéro (RZ)
Non-retour à zéro unipolaire (NRZ)
Dans ce type de signalisation unipolaire, un niveau élevé de données est représenté par une impulsion positive appelée Mark, qui a une durée T0égale à la durée du bit de symbole. Une entrée de données faible n'a pas d'impulsion.
La figure suivante illustre clairement cela.
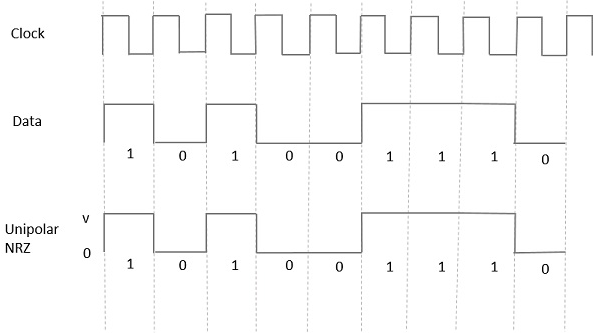
Advantages
Les avantages de Unipolar NRZ sont -
- C'est simple.
- Une bande passante moindre est requise.
Disadvantages
Les inconvénients de la NRZ unipolaire sont:
Aucune correction d'erreur effectuée.
La présence de composants basse fréquence peut provoquer une chute du signal.
Aucune horloge n'est présente.
Une perte de synchronisation est susceptible de se produire (en particulier pour les longues chaînes de 1s et 0s).
Retour unipolaire à zéro (RZ)
Dans ce type de signalisation unipolaire, un niveau élevé de données, bien que représenté par un Mark pulse, sa durée T0est inférieure à la durée du bit de symbole. La moitié de la durée du bit reste élevée mais elle revient immédiatement à zéro et montre l'absence d'impulsion pendant la moitié restante de la durée du bit.
Il est clairement compris à l'aide de la figure suivante.
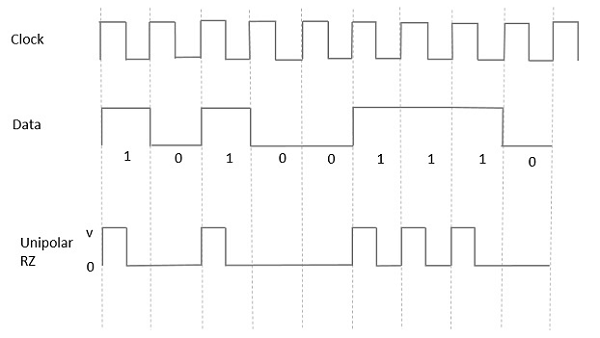
Advantages
Les avantages de Unipolar RZ sont -
- C'est simple.
- La raie spectrale présente au débit de symboles peut être utilisée comme horloge.
Disadvantages
Les inconvénients de Unipolar RZ sont -
- Aucune correction d'erreur.
- Occupe deux fois la bande passante comme NRZ unipolaire.
- Le statisme du signal est provoqué aux endroits où le signal est non nul à 0 Hz.
Signalisation polaire
Il existe deux méthodes de signalisation polaire. Ils sont -
- NRZ polaire
- Polar RZ
NRZ polaire
Dans ce type de signalisation polaire, un haut en données est représenté par une impulsion positive, tandis qu'un bas en données est représenté par une impulsion négative. La figure suivante illustre bien cela.
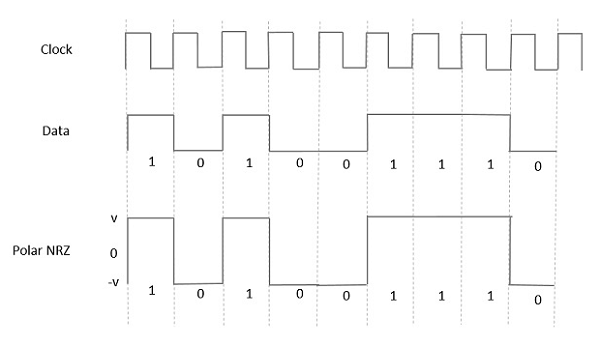
Advantages
Les avantages de Polar NRZ sont -
- C'est simple.
- Aucun composant basse fréquence n'est présent.
Disadvantages
Les inconvénients de Polar NRZ sont -
Aucune correction d'erreur.
Aucune horloge n'est présente.
Le statisme du signal est causé aux endroits où le signal est différent de zéro à 0 Hz.
Polar RZ
Dans ce type de signalisation polaire, un niveau élevé de données, bien que représenté par un Mark pulse, sa durée T0est inférieure à la durée du bit de symbole. La moitié de la durée du bit reste élevée mais elle revient immédiatement à zéro et montre l'absence d'impulsion pendant la moitié restante de la durée du bit.
Cependant, pour une entrée Low, une impulsion négative représente les données et le niveau zéro reste le même pendant l'autre moitié de la durée du bit. La figure suivante illustre cela clairement.
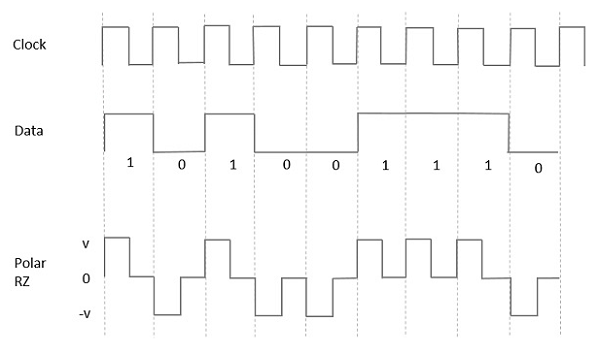
Advantages
Les avantages de Polar RZ sont -
- C'est simple.
- Aucun composant basse fréquence n'est présent.
Disadvantages
Les inconvénients de Polar RZ sont -
Aucune correction d'erreur.
Aucune horloge n'est présente.
Occupe deux fois la bande passante du Polar NRZ.
Le statisme du signal est causé aux endroits où le signal est différent de zéro à 0 Hz.
Signalisation bipolaire
Il s'agit d'une technique de codage qui a trois niveaux de tension à savoir +, - et 0. Un tel signal est appeléduo-binary signal.
Un exemple de ce type est Alternate Mark Inversion (AMI). Pour un1, le niveau de tension obtient une transition de + à - ou de - à +, ayant alterné 1sêtre de polarité égale. UNE0 aura un niveau de tension nul.
Même dans cette méthode, nous avons deux types.
- NRZ bipolaire
- Bipolaire RZ
À partir des modèles discutés jusqu'à présent, nous avons appris la différence entre NRZ et RZ. Cela se passe de la même manière ici aussi. La figure suivante illustre clairement cela.
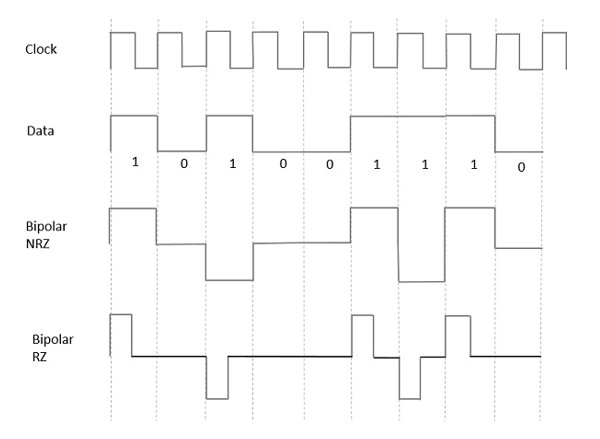
La figure ci-dessus présente les formes d'onde bipolaires NRZ et RZ. La durée de l'impulsion et la durée du bit de symbole sont égales dans le type NRZ, tandis que la durée de l'impulsion est la moitié de la durée du bit de symbole dans le type RZ.
Avantages
Voici les avantages -
C'est simple.
Aucun composant basse fréquence n'est présent.
Occupe une faible bande passante que les schémas NRZ unipolaires et polaires.
Cette technique convient à la transmission sur des lignes couplées en courant alternatif, car le statisme du signal ne se produit pas ici.
Une seule capacité de détection d'erreur est présente dans cela.
Désavantages
Voici les inconvénients -
- Aucune horloge n'est présente.
- De longues chaînes de données entraînent une perte de synchronisation.
Densité spectrale de puissance
La fonction qui décrit comment la puissance d'un signal a été distribuée à différentes fréquences, dans le domaine fréquentiel, est appelée Power Spectral Density (PSD).
PSD est la transformée de Fourier de l'auto-corrélation (similarité entre les observations). Il se présente sous la forme d'une impulsion rectangulaire.
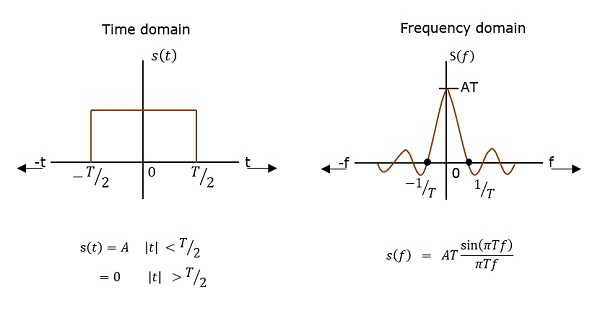
Dérivation PSD
Selon le théorème d'Einstein-Wiener-Khintchine, si la fonction d'auto-corrélation ou la densité spectrale de puissance d'un processus aléatoire est connue, l'autre peut être trouvée exactement.
Par conséquent, pour dériver la densité spectrale de puissance, nous utiliserons l'autocorrélation temporelle $ (R_x (\ tau)) $ d'un signal de puissance $ x (t) $ comme indiqué ci-dessous.
$ R_x (\ tau) = \ lim_ {T_p \ rightarrow \ infty} \ frac {1} {T_p} \ int _ {\ frac {{- T_p}} {2}} ^ {\ frac {T_p} {2}} x (t) x (t + \ tau) dt $
Puisque $ x (t) $ se compose d'impulsions, $ R_x (\ tau) $ peut s'écrire comme
$ R_x (\ tau) = \ frac {1} {T} \ displaystyle \ sum \ limits_ {n = - \ infty} ^ \ infty R_n \ delta (\ tau - nT) $
Où $ R_n = \ lim_ {N \ rightarrow \ infty} \ frac {1} {N} \ sum_ka_ka_ {k + n} $
Apprendre à savoir que $ R_n = R _ {- n} $ pour les signaux réels, nous avons
$ S_x (w) = \ frac {1} {T} (R_0 + 2 \ displaystyle \ sum \ limits_ {n = 1} ^ \ infty R_n \ cos nwT) $
Puisque le filtre d'impulsions a le spectre de $ (w) \ leftrightarrow f (t) $, nous avons
$ s_y (w) = \ milieu F (w) \ milieu ^ 2S_x (w) $
$ = \ frac {\ mid F (w) \ mid ^ 2} {T} (\ displaystyle \ sum \ limits_ {n = - \ infty} ^ \ infty R_ne ^ {- jnwT_ {b}}) $
$ = \ frac {\ mid F (w) \ mid ^ 2} {T} (R_0 + 2 \ displaystyle \ sum \ limits_ {n = 1} ^ \ infty R_n \ cos nwT) $
Par conséquent, nous obtenons l'équation de la densité spectrale de puissance. En utilisant cela, nous pouvons trouver le PSD de divers codes de ligne.
Encoding est le processus de conversion des données ou d'une séquence donnée de caractères, symboles, alphabets, etc., dans un format spécifié, pour la transmission sécurisée des données. Decoding est le processus inverse de codage qui consiste à extraire les informations du format converti.
Encodage des données
Le codage est le processus d'utilisation de divers modèles de niveaux de tension ou de courant pour représenter 1s et 0s des signaux numériques sur la liaison de transmission.
Les types courants de codage de ligne sont unipolaire, polaire, bipolaire et Manchester.
Techniques d'encodage
La technique de codage des données est divisée selon les types suivants, en fonction du type de conversion de données.
Analog data to Analog signals - Les techniques de modulation telles que la modulation d'amplitude, la modulation de fréquence et la modulation de phase des signaux analogiques relèvent de cette catégorie.
Analog data to Digital signals- Ce processus peut être qualifié de numérisation, qui est effectuée par modulation de code d'impulsion (PCM). Par conséquent, ce n'est rien d'autre qu'une modulation numérique. Comme nous l'avons déjà mentionné, l'échantillonnage et la quantification en sont les facteurs importants. La modulation Delta donne une meilleure sortie que PCM.
Digital data to Analog signals- Les techniques de modulation telles que la modulation par décalage d'amplitude (ASK), la modulation par décalage de fréquence (FSK), la modulation par décalage de phase (PSK), etc. relèvent de cette catégorie. Ceux-ci seront discutés dans les chapitres suivants.
Digital data to Digital signals- Ce sont dans cette section. Il existe plusieurs façons de mapper des données numériques sur des signaux numériques. Certains d'entre eux sont -
Non retour à zéro (NRZ)
NRZ Codes a 1 pour niveau de tension élevé et 0pour le niveau de basse tension. Le comportement principal des codes NRZ est que le niveau de tension reste constant pendant l'intervalle de bits. La fin ou le début d'un bit ne sera pas indiqué et il conservera le même état de tension, si la valeur du bit précédent et la valeur du bit actuel sont identiques.
La figure suivante explique le concept de codage NRZ.
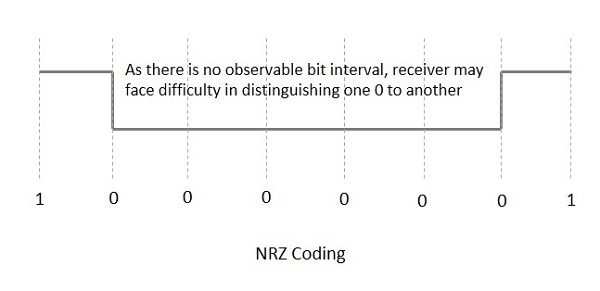
Si l'exemple ci-dessus est considéré, comme il y a une longue séquence de niveau de tension constant et que la synchronisation d'horloge peut être perdue en raison de l'absence d'intervalle de bits, il devient difficile pour le récepteur de faire la différence entre 0 et 1.
Il existe deux variantes de NRZ à savoir -
NRZ - L (NRZ - NIVEAU)
Il y a un changement de polarité du signal, uniquement lorsque le signal entrant passe de 1 à 0 ou de 0 à 1. C'est la même chose que NRZ, cependant, le premier bit du signal d'entrée doit avoir un changement de polarité.
NRZ - I (NRZ - INVERSÉ)
Si un 1se produit au niveau du signal entrant, puis il se produit une transition au début de l'intervalle de bits. Pour un0 au signal entrant, il n'y a pas de transition au début de l'intervalle binaire.
Les codes NRZ ont un disadvantage que la synchronisation de l'horloge de l'émetteur avec l'horloge du récepteur est complètement perturbée, lorsqu'il y a une chaîne de 1s et 0s. Par conséquent, une ligne d'horloge distincte doit être fournie.
Encodage biphasé
Le niveau du signal est vérifié deux fois pour chaque temps de bit, à la fois au départ et au milieu. Par conséquent, la fréquence d'horloge est le double de la vitesse de transfert de données et ainsi la vitesse de modulation est également doublée. L'horloge est tirée du signal lui-même. La bande passante requise pour ce codage est supérieure.
Il existe deux types de codage biphasé.
- Manchester biphasé
- Différentiel Manchester
Manchester biphasé
Dans ce type de codage, la transition se fait au milieu de l'intervalle binaire. La transition pour l'impulsion résultante est de haut vers bas au milieu de l'intervalle, pour le bit d'entrée 1. Alors que la transition est de bas vers haut pour le bit d'entrée0.
Différentiel Manchester
Dans ce type de codage, il se produit toujours une transition au milieu de l'intervalle de bits. S'il se produit une transition au début de l'intervalle de bits, le bit d'entrée est0. Si aucune transition ne se produit au début de l'intervalle de bits, le bit d'entrée est1.
La figure suivante illustre les formes d'onde du codage NRZ-L, NRZ-I, Manchester biphasé et Manchester différentiel pour différentes entrées numériques.
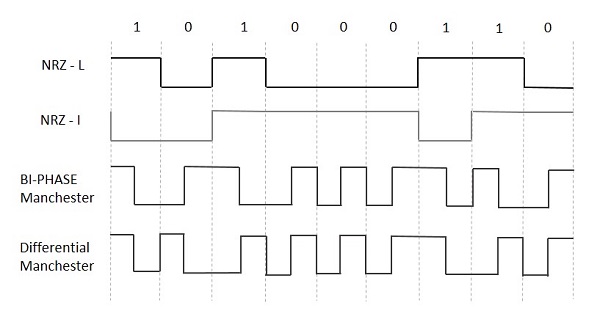
Codage de bloc
Parmi les types de codage par blocs, les plus connus sont le codage 4B / 5B et le codage 8B / 6T. Le nombre de bits est traité de différentes manières, dans ces deux processus.
Encodage 4B / 5B
Dans le codage Manchester, pour envoyer les données, les horloges à double vitesse sont nécessaires plutôt que le codage NRZ. Ici, comme son nom l'indique, 4 bits de code sont mappés avec 5 bits, avec un nombre minimum de1 bits dans le groupe.
Le problème de synchronisation d'horloge dans le codage NRZ-I est évité en attribuant un mot équivalent de 5 bits à la place de chaque bloc de 4 bits consécutifs. Ces mots de 5 bits sont prédéterminés dans un dictionnaire.
L'idée de base de la sélection d'un code 5 bits est qu'il devrait avoir one leading 0 et il devrait avoir no more than two trailing 0s. Par conséquent, ces mots sont choisis de telle sorte que deux transactions aient lieu par bloc de bits.
Encodage 8B / 6T
Nous avons utilisé deux niveaux de tension pour envoyer un seul bit sur un seul signal. Mais si nous utilisons plus de 3 niveaux de tension, nous pouvons envoyer plus de bits par signal.
Par exemple, si 6 niveaux de tension sont utilisés pour représenter 8 bits sur un seul signal, alors un tel codage est appelé codage 8B / 6T. Par conséquent, dans cette méthode, nous avons jusqu'à 729 (3 ^ 6) combinaisons pour le signal et 256 (2 ^ 8) combinaisons pour les bits.
Ce sont les techniques les plus utilisées pour convertir des données numériques en signaux numériques en les compressant ou en les codant pour une transmission fiable des données.
Après avoir traversé différents types de techniques de codage, nous avons une idée sur la façon dont les données sont sujettes à la distorsion et comment les mesures sont prises pour éviter qu'elles ne soient affectées afin d'établir une communication fiable.
Il y a une autre distorsion importante qui est la plus susceptible de se produire, appelée Inter-Symbol Interference (ISI).
Interférence entre symboles
Il s'agit d'une forme de distorsion d'un signal, dans laquelle un ou plusieurs symboles interfèrent avec les signaux suivants, provoquant du bruit ou délivrant une sortie médiocre.
Causes de l'ISI
Les principales causes de l'ISI sont -
- Propagation multi-chemins
- Fréquence non linéaire dans les canaux
L'ISI est indésirable et doit être complètement éliminé pour obtenir une sortie propre. Les causes de l'ISI doivent également être résolues afin d'atténuer son effet.
Pour visualiser l'ISI sous une forme mathématique présente dans la sortie du récepteur, nous pouvons considérer la sortie du récepteur.
La sortie du filtre récepteur $ y (t) $ est échantillonnée au temps $ t_i = iT_b $ (avec i prenant des valeurs entières), ce qui donne -
$ y (t_i) = \ mu \ displaystyle \ sum \ limits_ {k = - \ infty} ^ {\ infty} a_kp (iT_b - kT_b) $
$ = \ mu a_i + \ mu \ displaystyle \ sum \ limits_ {k = - \ infty \\ k \ neq? i} ^ {\ infty} a_kp (iT_b - kT_b) $
Dans l'équation ci-dessus, le premier terme $ \ mu a_i $ est produit par le ith bit transmis.
Le deuxième terme représente l'effet résiduel de tous les autres bits transmis sur le décodage du ithbit. Cet effet résiduel est appeléInter Symbol Interference.
En l'absence d'ISI, la sortie sera -
$$ y (t_i) = \ mu a_i $$
Cette équation montre que le ithle bit transmis est correctement reproduit. Cependant, la présence d'ISI introduit des erreurs de bits et des distorsions dans la sortie.
Lors de la conception de l'émetteur ou du récepteur, il est important de minimiser les effets d'ISI, afin de recevoir la sortie avec le moins d'erreur possible.
Codage corrélatif
Jusqu'à présent, nous avons discuté du fait que l'ISI est un phénomène indésirable et dégrade le signal. Mais le même ISI s'il est utilisé de manière contrôlée, est possible pour atteindre un débit binaire de2W bits par seconde dans un canal de bande passante WHertz. Un tel schéma est appelé commeCorrelative Coding ou Partial response signaling schemes.
Etant donné que la quantité d'ISI est connue, il est facile de concevoir le récepteur selon l'exigence de manière à éviter l'effet d'ISI sur le signal. L'idée de base du codage corrélatif est obtenue en considérant un exemple deDuo-binary Signaling.
Signalisation Duo-binaire
Le nom duo-binaire signifie doubler la capacité de transmission du système binaire. Pour comprendre cela, considérons une séquence d'entrée binaire{ak} composé de chiffres binaires non corrélés ayant chacun une durée Tasecondes. En cela, le signal1 est représenté par un +1 volt et le symbole 0 par un -1 volt.
Par conséquent, la sortie du codeur duo-binaire ck est donné comme la somme du chiffre binaire actuel ak et la valeur précédente ak-1 comme indiqué dans l'équation suivante.
$$ c_k = a_k + a_ {k-1} $$
L'équation ci-dessus indique que la séquence d'entrée de la séquence binaire non corrélée {ak} se transforme en une séquence d'impulsions à trois niveaux corrélées {ck}. Cette corrélation entre les impulsions peut être comprise comme introduisant de manière artificielle ISI dans le signal émis.
Motif des yeux
Un moyen efficace d'étudier les effets de l'ISI est Eye Pattern. Le nom Eye Pattern a été donné à partir de sa ressemblance avec l'œil humain pour les ondes binaires. La région intérieure du motif oculaire est appelée leeye opening. La figure suivante montre l'image d'un motif d'œil.
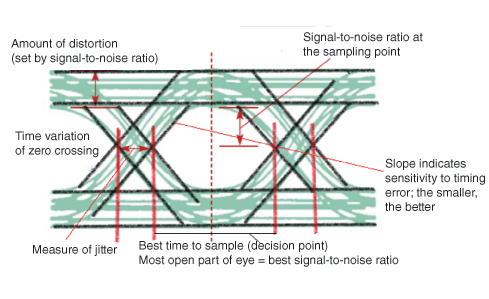
Jitter est la variation à court terme de l'instant du signal numérique, à partir de sa position idéale, qui peut conduire à des erreurs de données.
Lorsque l'effet de l'ISI augmente, les traces de la partie supérieure à la partie inférieure de l'ouverture de l'œil augmentent et l'œil se ferme complètement, si l'ISI est très élevé.
Un motif d'œil fournit les informations suivantes sur un système particulier.
Des motifs oculaires réels sont utilisés pour estimer le taux d'erreur sur les bits et le rapport signal sur bruit.
La largeur de l'ouverture de l'œil définit l'intervalle de temps sur lequel l'onde reçue peut être échantillonnée sans erreur d'ISI.
Le moment où l'ouverture des yeux est large sera le moment préféré pour l'échantillonnage.
La vitesse de fermeture de l'œil, en fonction du temps d'échantillonnage, détermine la sensibilité du système à l'erreur de synchronisation.
La hauteur de l'ouverture des yeux, à un moment d'échantillonnage spécifié, définit la marge sur le bruit.
Par conséquent, l'interprétation de la configuration des yeux est une considération importante.
Égalisation
Pour établir une communication fiable, nous devons avoir un résultat de qualité. Les pertes de transmission du canal et d'autres facteurs affectant la qualité du signal doivent être traités. La perte la plus fréquente, comme nous l'avons vu, est l'ISI.
Pour rendre le signal exempt d'ISI et pour assurer un rapport signal / bruit maximal, nous devons implémenter une méthode appelée Equalization. La figure suivante montre un égaliseur dans la partie récepteur du système de communication.
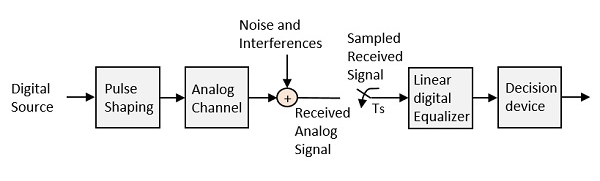
Le bruit et les interférences indiqués sur la figure sont susceptibles de se produire pendant la transmission. Le répéteur régénératif possède un circuit égaliseur, qui compense les pertes de transmission en façonnant le circuit. L'égaliseur peut être implémenté.
Probabilité d'erreur et figure de mérite
La vitesse à laquelle les données peuvent être communiquées est appelée data rate. Le taux auquel l'erreur se produit dans les bits, lors de la transmission de données est appelé leBit Error Rate (BER).
La probabilité d'occurrence du BER est la Error Probability. L'augmentation du rapport signal / bruit (SNR) diminue le BER, d'où la probabilité d'erreur est également diminuée.
Dans un récepteur analogique, le figure of meritau processus de détection peut être appelé le rapport entre le SNR de sortie et le SNR d'entrée. Une plus grande valeur de la figure de mérite sera un avantage.
Les signaux numériques-analogiques constituent la prochaine conversion dont nous parlerons dans ce chapitre. Ces techniques sont également appelées commeDigital Modulation techniques.
Digital Modulationoffre plus de capacité d'information, une haute sécurité des données, une disponibilité plus rapide du système avec une communication de grande qualité. Par conséquent, les techniques de modulation numérique ont une plus grande demande, pour leur capacité à transporter de plus grandes quantités de données que les techniques de modulation analogique.
Il existe de nombreux types de techniques de modulation numérique ainsi que leurs combinaisons, en fonction des besoins. De tous, nous discuterons des plus importants.
ASK - Incrustation par décalage d'amplitude
L'amplitude de la sortie résultante dépend des données d'entrée, qu'il s'agisse d'un niveau zéro ou d'une variation positive et négative, en fonction de la fréquence porteuse.
FSK - Incrustation par décalage de fréquence
La fréquence du signal de sortie sera soit élevée, soit basse, selon les données d'entrée appliquées.
PSK - Clé à décalage de phase
La phase du signal de sortie est décalée en fonction de l'entrée. Il s'agit principalement de deux types, à savoir la modulation par décalage de phase binaire (BPSK) et la modulation par décalage de phase en quadrature (QPSK), en fonction du nombre de déphasages. L'autre est la modulation par décalage de phase différentielle (DPSK) qui change la phase en fonction de la valeur précédente.
Encodage M-aire
Les techniques de codage M-aire sont les méthodes dans lesquelles plus de deux bits sont amenés à émettre simultanément sur un seul signal. Cela contribue à la réduction de la bande passante.
Les types de techniques M-ary sont -
- DEMANDEZ M-ary
- M-ary FSK
- M-aire PSK
Tous ces éléments sont traités dans les chapitres suivants.
Amplitude Shift Keying (ASK) est un type de modulation d'amplitude qui représente les données binaires sous la forme de variations de l'amplitude d'un signal.
Tout signal modulé a une porteuse haute fréquence. Le signal binaire lorsqu'il est modulé ASK, donne unzero la valeur pour Low entrée pendant qu'il donne le carrier output pour High contribution.
La figure suivante représente la forme d'onde modulée ASK avec son entrée.
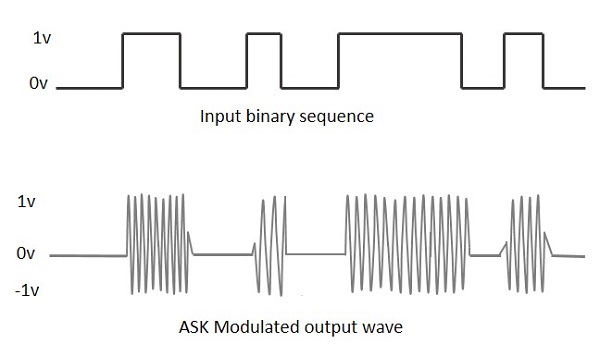
Pour trouver le processus d'obtention de cette onde modulée ASK, apprenons le fonctionnement du modulateur ASK.
Modulateur ASK
Le schéma de principe du modulateur ASK comprend le générateur de signal de porteuse, la séquence binaire du signal de message et le filtre à bande limitée. Voici le schéma de principe du modulateur ASK.
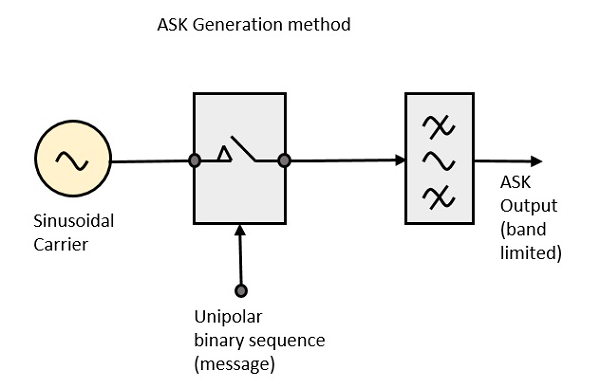
Le générateur de porteuse, envoie une porteuse haute fréquence continue. La séquence binaire du signal de message fait de l'entrée unipolaire une valeur haute ou basse. Le signal haut ferme le commutateur, permettant une onde porteuse. Par conséquent, la sortie sera le signal porteur à une entrée élevée. Lorsqu'il y a une faible entrée, l'interrupteur s'ouvre, permettant à aucune tension d'apparaître. Par conséquent, la sortie sera faible.
Le filtre de limitation de bande façonne l'impulsion en fonction des caractéristiques d'amplitude et de phase du filtre de limitation de bande ou du filtre de mise en forme d'impulsion.
Démodulateur ASK
Il existe deux types de techniques de démodulation ASK. Ils sont -
- Démodulation / détection ASK asynchrone
- Démodulation / détection ASK synchrone
La fréquence d'horloge de l'émetteur lorsqu'elle correspond à la fréquence d'horloge du récepteur, elle est connue sous le nom de Synchronous method, à mesure que la fréquence se synchronise. Sinon, il est connu commeAsynchronous.
Démodulateur ASK asynchrone
Le détecteur ASK asynchrone se compose d'un redresseur demi-onde, d'un filtre passe-bas et d'un comparateur. Voici le schéma de principe pour le même.
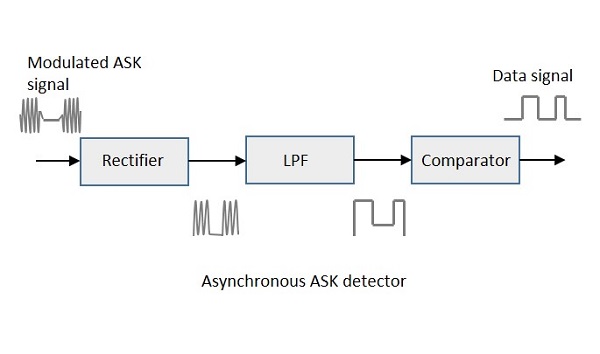
Le signal ASK modulé est transmis au redresseur demi-onde, qui délivre une demi-sortie positive. Le filtre passe-bas supprime les fréquences les plus élevées et donne une sortie d'enveloppe détectée à partir de laquelle le comparateur délivre une sortie numérique.
Démodulateur ASK synchrone
Le détecteur ASK synchrone comprend un détecteur à loi carrée, un filtre passe-bas, un comparateur et un limiteur de tension. Voici le schéma de principe pour le même.
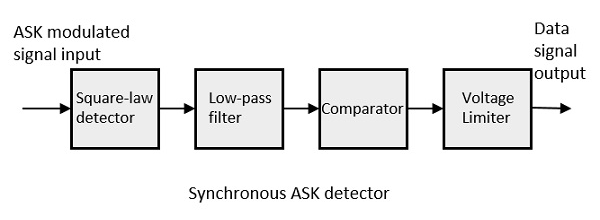
Le signal d'entrée modulé ASK est transmis au détecteur de loi Square. Un détecteur à loi carrée est un détecteur dont la tension de sortie est proportionnelle au carré de la tension d'entrée modulée en amplitude. Le filtre passe-bas minimise les fréquences les plus élevées. Le comparateur et le limiteur de tension aident à obtenir une sortie numérique propre.
Frequency Shift Keying (FSK)est la technique de modulation numérique dans laquelle la fréquence du signal porteur varie en fonction des changements de signal numérique. FSK est un schéma de modulation de fréquence.
La sortie d'une onde modulée FSK est haute en fréquence pour une entrée binaire High et basse en fréquence pour une entrée binaire Low. Le binaire1s et 0s sont appelées fréquences Mark et Space.
L'image suivante est la représentation schématique de la forme d'onde modulée FSK avec son entrée.
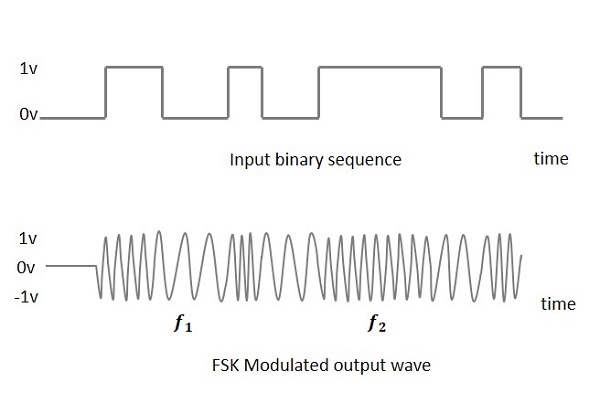
Pour connaître le processus d'obtention de cette onde modulée FSK, informez-nous sur le fonctionnement d'un modulateur FSK.
Modulateur FSK
Le schéma de principe du modulateur FSK comprend deux oscillateurs avec une horloge et la séquence binaire d'entrée. Voici son schéma de principe.

Les deux oscillateurs, produisant des signaux de fréquence supérieure et inférieure, sont connectés à un commutateur avec une horloge interne. Pour éviter les discontinuités de phase brusques de la forme d'onde de sortie lors de la transmission du message, une horloge est appliquée aux deux oscillateurs, en interne. La séquence d'entrée binaire est appliquée à l'émetteur de manière à choisir les fréquences en fonction de l'entrée binaire.
Démodulateur FSK
Il existe différentes méthodes pour démoduler une onde FSK. Les principales méthodes de détection FSK sontasynchronous detector et synchronous detector. Le détecteur synchrone est un détecteur cohérent, tandis que le détecteur asynchrone est un détecteur non cohérent.
Détecteur FSK asynchrone
Le schéma de principe du détecteur FSK asynchrone se compose de deux filtres passe-bande, de deux détecteurs d'enveloppe et d'un circuit de décision. Voici la représentation schématique.
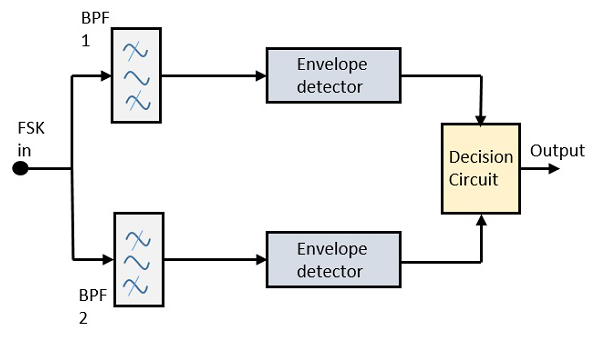
Le signal FSK passe par les deux filtres passe-bande (BPF), réglés sur Space et Markfréquences. La sortie de ces deux BPF ressemble au signal ASK, qui est donné au détecteur d'enveloppe. Le signal dans chaque détecteur d'enveloppe est modulé de manière asynchrone.
Le circuit de décision choisit quelle sortie est la plus probable et la sélectionne parmi l'un quelconque des détecteurs d'enveloppe. Il remodèle également la forme d'onde en une forme rectangulaire.
Détecteur FSK synchrone
Le schéma de principe du détecteur FSK synchrone se compose de deux mélangeurs avec des circuits oscillateurs locaux, deux filtres passe-bande et un circuit de décision. Voici la représentation schématique.
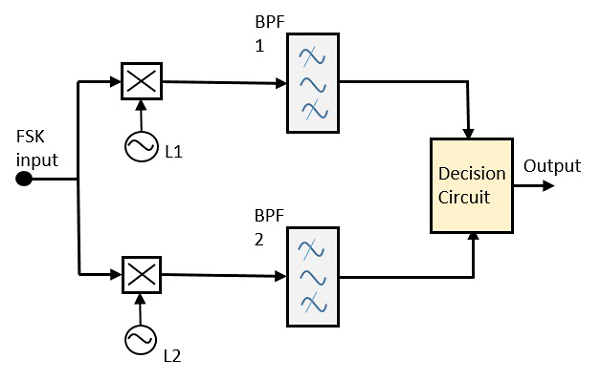
L'entrée de signal FSK est donnée aux deux mélangeurs avec des circuits d'oscillateur locaux. Ces deux sont connectés à deux filtres passe-bande. Ces combinaisons agissent comme des démodulateurs et le circuit de décision choisit quelle sortie est la plus probable et la sélectionne parmi l'un quelconque des détecteurs. Les deux signaux ont une séparation de fréquence minimale.
Pour les deux démodulateurs, la bande passante de chacun d'eux dépend de leur débit binaire. Ce démodulateur synchrone est un peu complexe que les démodulateurs de type asynchrone.
Phase Shift Keying (PSK)est la technique de modulation numérique dans laquelle la phase du signal de porteuse est modifiée en faisant varier les entrées sinus et cosinus à un instant particulier. La technique PSK est largement utilisée pour les réseaux locaux sans fil, les opérations biométriques et sans contact, ainsi que les communications RFID et Bluetooth.
PSK est de deux types, en fonction des phases, le signal est décalé. Ils sont -
Clé à décalage de phase binaire (BPSK)
Ceci est également appelé PSK 2 phases ou clé d'inversion de phase. Dans cette technique, la porteuse sinusoïdale prend deux inversions de phase telles que 0 ° et 180 °.
BPSK est fondamentalement un schéma de modulation DSBSC (Double Side Band Suppressed Carrier), le message étant l'information numérique.
Clé à décalage de phase en quadrature (QPSK)
Il s'agit de la technique de modulation par décalage de phase, dans laquelle la porteuse d'onde sinusoïdale prend quatre inversions de phase telles que 0 °, 90 °, 180 ° et 270 °.
Si ce type de techniques est encore étendu, PSK peut également être fait par huit ou seize valeurs, selon les besoins.
Modulateur BPSK
Le schéma de principe de la modulation par décalage de phase binaire se compose du modulateur d'équilibre qui a l'onde sinusoïdale porteuse comme une entrée et la séquence binaire comme l'autre entrée. Voici la représentation schématique.
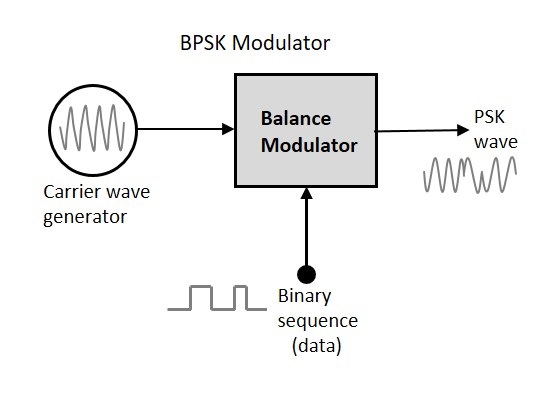
La modulation de BPSK se fait à l'aide d'un modulateur d'équilibre, qui multiplie les deux signaux appliqués à l'entrée. Pour une entrée binaire nulle, la phase sera0° et pour une entrée élevée, l'inversion de phase est de 180°.
Voici la représentation schématique de l'onde de sortie modulée BPSK avec son entrée donnée.
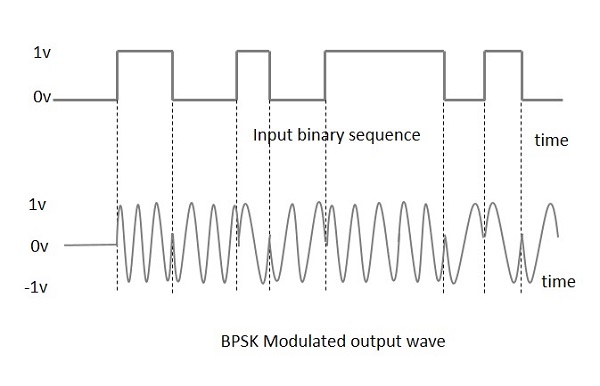
L'onde sinusoïdale de sortie du modulateur sera la porteuse d'entrée directe ou la porteuse d'entrée inversée (déphasée à 180 °), qui est fonction du signal de données.
Démodulateur BPSK
Le schéma de principe du démodulateur BPSK se compose d'un mélangeur avec un circuit oscillateur local, un filtre passe-bande, un circuit de détection à deux entrées. Le diagramme est le suivant.
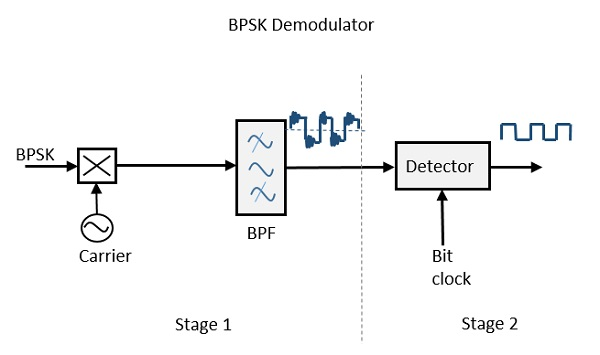
En récupérant le signal de message à bande limitée, à l'aide du circuit mélangeur et du filtre passe-bande, la première étape de démodulation est terminée. Le signal de bande de base qui est limité en bande est obtenu et ce signal est utilisé pour régénérer le train de bits de message binaire.
Dans l'étape suivante de démodulation, la fréquence d'horloge binaire est nécessaire au niveau du circuit de détection pour produire le signal de message binaire d'origine. Si le débit binaire est un sous-multiple de la fréquence porteuse, alors la régénération de l'horloge binaire est simplifiée. Pour rendre le circuit facilement compréhensible, un circuit de décision peut également être inséré au 2 ème étage de détection.
le Quadrature Phase Shift Keying (QPSK) est une variante de BPSK, et c'est aussi un schéma de modulation à double bande latérale supprimée (DSBSC), qui envoie deux bits d'informations numériques à la fois, appelé comme bigits.
Au lieu de convertir des bits numériques en une série de flux numériques, il les convertit en paires de bits. Cela réduit le débit binaire des données de moitié, ce qui laisse de l'espace pour les autres utilisateurs.
Modulateur QPSK
Le modulateur QPSK utilise un séparateur de bits, deux multiplicateurs avec oscillateur local, un convertisseur série-parallèle 2 bits et un circuit d'été. Voici le schéma de principe pour le même.

A l'entrée du modulateur, bits pairs du signal de message ( par exemple, 2 ème bit, 4 ème bit, 6 ème bit, etc.) et les bits impairs ( par exemple, premier bit, 3 ème bit, 5 ème bit, etc.) sont séparés par le séparateur de bits et sont multipliés par la même porteuse pour générer des BPSK impairs (appelés commePSKI) et même BPSK (appelé comme PSKQ). lePSKQ le signal est de toute façon déphasé de 90 ° avant d'être modulé.
La forme d'onde QPSK pour une entrée à deux bits est la suivante, qui montre le résultat modulé pour différentes instances d'entrées binaires.
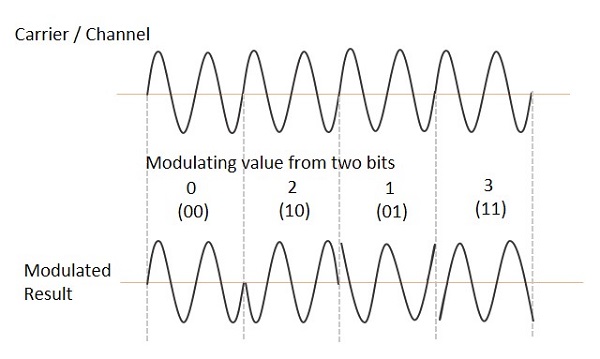
Démodulateur QPSK
Le démodulateur QPSK utilise deux circuits de démodulateur de produit avec un oscillateur local, deux filtres passe-bande, deux circuits intégrateurs et un convertisseur parallèle-série 2 bits. Voici le diagramme pour le même.
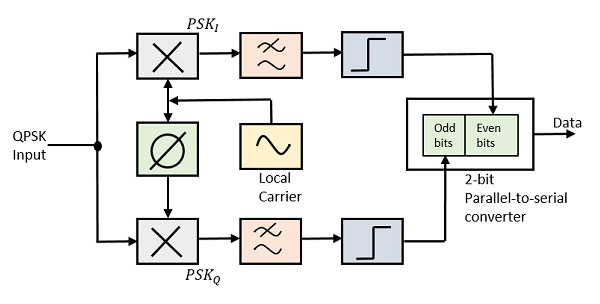
Les deux détecteurs de produit à l'entrée du démodulateur démodulent simultanément les deux signaux BPSK. La paire de bits est ici récupérée à partir des données d'origine. Ces signaux, après traitement, sont transmis au convertisseur parallèle-série.
Dans Differential Phase Shift Keying (DPSK)la phase du signal modulé est décalée par rapport à l'élément de signal précédent. Aucun signal de référence n'est pris en compte ici. La phase du signal suit l'état haut ou bas de l'élément précédent. Cette technique DPSK ne nécessite pas d'oscillateur de référence.
La figure suivante représente la forme d'onde du modèle de DPSK.
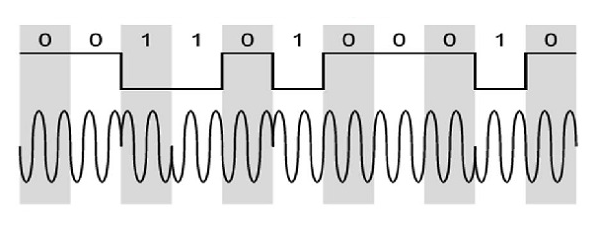
On voit à partir de la figure ci-dessus que, si le bit de données est Low, c'est-à-dire 0, alors la phase du signal n'est pas inversée, mais continue telle qu'elle était. Si les données sont élevées, c'est-à-dire 1, alors la phase du signal est inversée, comme avec NRZI, inversée sur 1 (une forme de codage différentiel).
Si nous observons la forme d'onde ci-dessus, nous pouvons dire que l'état High représente un M dans le signal modulant et l'état bas représente un W dans le signal modulant.
Modulateur DPSK
DPSK est une technique de BPSK, dans laquelle il n'y a pas de signal de phase de référence. Ici, le signal émis lui-même peut être utilisé comme signal de référence. Voici le schéma du modulateur DPSK.
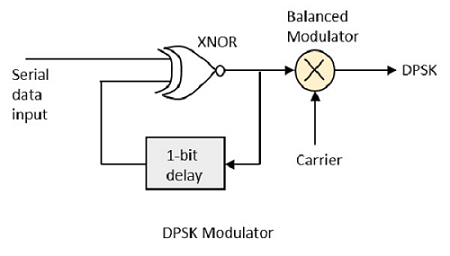
DPSK code deux signaux distincts, c'est-à-dire la porteuse et le signal de modulation avec un déphasage de 180 ° chacun. L'entrée de données série est transmise à la porte XNOR et la sortie est à nouveau renvoyée à l'autre entrée via un délai de 1 bit. La sortie de la porte XNOR avec le signal de porteuse est donnée au modulateur d'équilibre, pour produire le signal modulé DPSK.
Démodulateur DPSK
Dans le démodulateur DPSK, la phase du bit inversé est comparée à la phase du bit précédent. Voici le schéma de principe du démodulateur DPSK.

D'après la figure ci-dessus, il est évident que le modulateur d'équilibre reçoit le signal DPSK avec une entrée de retard de 1 bit. Ce signal est fait pour se limiter à des fréquences plus basses à l'aide de LPF. Ensuite, il est transmis à un circuit de mise en forme, qui est un comparateur ou un circuit de déclenchement de Schmitt, pour récupérer les données binaires d'origine en tant que sortie.
Le mot binaire représente deux bits. M représente un chiffre qui correspond au nombre de conditions, niveaux ou combinaisons possibles pour un nombre donné de variables binaires.
C'est le type de technique de modulation numérique utilisé pour la transmission de données dans laquelle au lieu d'un bit, deux bits ou plus sont transmis à la fois. Comme un seul signal est utilisé pour une transmission à bits multiples, la bande passante du canal est réduite.
Équation M-aire
Si un signal numérique est donné sous quatre conditions, telles que les niveaux de tension, les fréquences, les phases et l'amplitude, alors M = 4.
Le nombre de bits nécessaires pour produire un nombre donné de conditions est exprimé mathématiquement par
$$ N = \ log_ {2} {M} $$
Où
N est le nombre de bits nécessaires
M est le nombre de conditions, niveaux ou combinaisons possibles avec N morceaux.
L'équation ci-dessus peut être réorganisée comme
$$ 2 ^ N = M $$
Par exemple, avec deux bits, 22 = 4 les conditions sont possibles.
Types de techniques M-aire
En général, les techniques de modulation multi-niveaux (M-aire) sont utilisées dans les communications numériques car les entrées numériques avec plus de deux niveaux de modulation sont autorisées sur l'entrée de l'émetteur. Par conséquent, ces techniques sont efficaces en bande passante.
Il existe de nombreuses techniques de modulation M-aire. Certaines de ces techniques modulent un paramètre du signal porteur, tel que l'amplitude, la phase et la fréquence.
DEMANDEZ M-ary
C'est ce qu'on appelle la modulation par décalage d'amplitude M-aire (M-ASK) ou la modulation d'amplitude d'impulsion M-aire (PAM).
le amplitude du signal porteur, prend M différents niveaux.
Représentation de M-ary ASK
$ S_m (t) = A_mcos (2 \ pi f_ct) \ quad A_m \ epsilon {(2m - 1 - M) \ Delta, m = 1,2 ... \: .M} \ quad et \ quad 0 \ leq t \ leq T_s $
Certaines caractéristiques importantes de M-ary ASK sont:
- Cette méthode est également utilisée dans PAM.
- Sa mise en œuvre est simple.
- M-ary ASK est sensible au bruit et à la distorsion.
M-ary FSK
C'est ce qu'on appelle la modulation par décalage de fréquence M-aire (M-aire FSK).
le frequency du signal porteur, prend M différents niveaux.
Représentation de M-ary FSK
$ S_i (t) = \ sqrt {\ frac {2E_s} {T_s}} \ cos \ left (\ frac {\ pi} {T_s} \ left (n_c + i \ right) t \ right) $ 0 \ leq t \ leq T_s \ quad et \ quad i = 1,2,3 ... \: ..M $
Où $ f_c = \ frac {n_c} {2T_s} $ pour un entier fixe n.
Certaines caractéristiques importantes de M-ary FSK sont:
Pas sensible au bruit autant que DEMANDER.
Le transmis M nombre de signaux sont égaux en énergie et en durée.
Les signaux sont séparés par $ \ frac {1} {2T_s} $ Hz rendant les signaux orthogonaux entre eux.
Depuis M les signaux sont orthogonaux, il n'y a pas d'encombrement dans l'espace du signal.
L'efficacité de la bande passante de M-ary FSK diminue et l'efficacité énergétique augmente avec l'augmentation de M.
M-aire PSK
C'est ce qu'on appelle la modulation par décalage de phase M-aire (M-aire PSK).
le phase du signal porteur, prend M différents niveaux.
Représentation de M-ary PSK
$ S_i (t) = \ sqrt {\ frac {2E} {T}} \ cos \ left (w_o t + \ phi _it \ right) $ $ 0 \ leq t \ leq T \ quad et \ quad i = 1,2 ... M $
$$ \ phi _i \ left (t \ right) = \ frac {2 \ pi i} {M} \ quad où \ quad i = 1,2,3 ... \: ... M $$
Certaines caractéristiques importantes de M-ary PSK sont:
L'enveloppe est constante avec plus de possibilités de phase.
Cette méthode a été utilisée pendant les premiers jours de la communication spatiale.
De meilleures performances que ASK et FSK.
Erreur d'estimation de phase minimale au niveau du récepteur.
L'efficacité de la bande passante du M-ary PSK diminue et l'efficacité énergétique augmente avec l'augmentation de M.
Jusqu'à présent, nous avons discuté de différentes techniques de modulation. Le résultat de toutes ces techniques est une séquence binaire, représentée par1s et 0s. Ces informations binaires ou numériques ont de nombreux types et formes, qui sont discutés plus loin.
L'information est la source d'un système de communication, qu'il soit analogique ou numérique. Information theory est une approche mathématique de l'étude du codage de l'information ainsi que de la quantification, du stockage et de la communication de l'information.
Conditions de survenue des événements
Si l'on considère un événement, il y a trois conditions d'occurrence.
Si l'événement ne s'est pas produit, il y a une condition de uncertainty.
Si l'événement vient de se produire, il y a une condition de surprise.
Si l'événement s'est produit, il y a un certain temps, il y a une condition pour avoir information.
Ces trois événements se produisent à des moments différents. La différence de ces conditions nous permet d'acquérir des connaissances sur les probabilités de survenance d'événements.
Entropie
Lorsque nous observons les possibilités d'occurrence d'un événement, à quel point il serait surprenant ou incertain, cela signifie que nous essayons d'avoir une idée sur le contenu moyen de l'information de la source de l'événement.
Entropy peut être défini comme une mesure du contenu d'information moyen par symbole source. Claude Shannon, le «père de la théorie de l'information», en a fourni une formule comme -
$$ H = - \ sum_ {i} p_i \ log_ {b} p_i $$
Où pi est la probabilité d'occurrence du numéro de caractère i à partir d'un flux donné de personnages et best la base de l'algorithme utilisé. Par conséquent, cela est également appelé commeShannon’s Entropy.
La quantité d'incertitude restante sur l'entrée de canal après avoir observé la sortie de canal, est appelée Conditional Entropy. Il est noté $ H (x \ mid y) $
Information mutuelle
Considérons un canal dont la sortie est Y et l'entrée est X
Soit l'entropie pour l'incertitude antérieure X = H(x)
(Ceci est supposé avant l'application de l'entrée)
Pour connaître l'incertitude de la sortie, une fois l'entrée appliquée, considérons l'entropie conditionnelle, étant donné que Y = yk
$$ H \ left (x \ mid y_k \ right) = \ sum_ {j = 0} ^ {j - 1} p \ left (x_j \ mid y_k \ right) \ log_ {2} \ left [\ frac {1 } {p (x_j \ mid y_k)} \ right] $$
Ceci est une variable aléatoire pour $ H (X \ mid y = y_0) \: ... \: ... \: ... \: ... \: ... \: H (X \ mid y = y_k) $ avec des probabilités $ p (y_0) \: ... \: ... \: ... \: ... \: p (y_ {k-1)} $ respectivement.
La valeur moyenne de $ H (X \ mid y = y_k) $ pour l'alphabet de sortie y est -
$ H \ left (X \ mid Y \ right) = \ displaystyle \ sum \ limits_ {k = 0} ^ {k - 1} H \ left (X \ mid y = y_k \ right) p \ left (y_k \ right) ) $
$ = \ displaystyle \ sum \ limits_ {k = 0} ^ {k - 1} \ displaystyle \ sum \ limits_ {j = 0} ^ {j - 1} p \ left (x_j \ mid y_k \ right) p \ left (y_k \ right) \ log_ {2} \ left [\ frac {1} {p \ left (x_j \ mid y_k \ right)} \ right] $
$ = \ displaystyle \ sum \ limits_ {k = 0} ^ {k - 1} \ displaystyle \ sum \ limits_ {j = 0} ^ {j - 1} p \ left (x_j, y_k \ right) \ log_ {2 } \ left [\ frac {1} {p \ left (x_j \ mid y_k \ right)} \ right] $
Maintenant, en considérant les deux conditions d'incertitude (avant et après l'application des entrées), nous arrivons à savoir que la différence, c'est-à-dire $ H (x) - H (x \ mid y) $ doit représenter l'incertitude sur l'entrée de canal qui est résolue en observant la sortie du canal.
Ceci est appelé comme le Mutual Information de la chaîne.
En désignant les informations mutuelles comme $ I (x; y) $, nous pouvons écrire le tout dans une équation, comme suit
$$ I (x; y) = H (x) - H (x \ mid y) $$
Il s'agit donc de la représentation équationnelle de l'information mutuelle.
Propriétés des informations mutuelles
Ce sont les propriétés de l'information mutuelle.
Les informations mutuelles d'un canal sont symétriques.
$$ I (x; y) = I (y; x) $$
Les informations mutuelles ne sont pas négatives.
$$ I (x; y) \ geq 0 $$
Les informations mutuelles peuvent être exprimées en termes d'entropie de la sortie du canal.
$$ I (x; y) = H (y) - H (y \ milieu x) $$
Où $ H (y \ mid x) $ est une entropie conditionnelle
Les informations mutuelles d'un canal sont liées à l'entropie conjointe de l'entrée de canal et de la sortie de canal.
$$ I (x; y) = H (x) + H (y) - H (x, y) $$
Où l'entropie conjointe $ H (x, y) $ est définie par
$$ H (x, y) = \ displaystyle \ sum \ limits_ {j = 0} ^ {j-1} \ displaystyle \ sum \ limits_ {k = 0} ^ {k-1} p (x_j, y_k) \ log_ {2} \ left (\ frac {1} {p \ left (x_i, y_k \ right)} \ right) $$
Capacité de canal
Nous avons jusqu'ici discuté de l'information mutuelle. L'information mutuelle moyenne maximale, à un instant d'un intervalle de signalisation, lorsqu'elle est transmise par un canal discret sans mémoire, les probabilités du taux de transmission fiable maximale des données, peuvent être comprises commechannel capacity.
Il est désigné par C et est mesurée en bits per channel utilisation.
Source discrète sans mémoire
Une source à partir de laquelle les données sont émises à intervalles successifs, qui est indépendante des valeurs précédentes, peut être appelée discrete memoryless source.
Cette source est discrète car elle n'est pas considérée pour un intervalle de temps continu, mais à des intervalles de temps discrets. Cette source est sans mémoire car elle est fraîche à chaque instant, sans tenir compte des valeurs précédentes.
Le Code produit par une source discrète sans mémoire, doit être représenté efficacement, ce qui est un problème important dans les communications. Pour ce faire, il existe des mots de code, qui représentent ces codes sources.
Par exemple, en télégraphie, nous utilisons le code Morse, dans lequel les alphabets sont désignés par Marks et Spaces. Si la lettreE est considéré, qui est le plus utilisé, il est noté “.” Alors que la lettre Q qui est rarement utilisé, est désigné par “--.-”
Jetons un coup d'œil au diagramme.
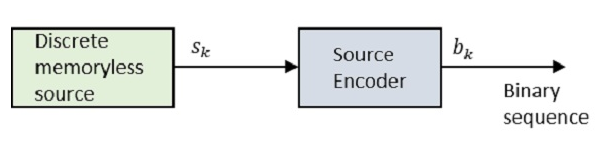
Où Sk est la sortie de la source discrète sans mémoire et bk est la sortie du codeur source qui est représentée par 0s et 1s.
La séquence codée est telle qu'elle est convenablement décodée au niveau du récepteur.
Supposons que la source ait un alphabet avec k symboles différents et que le kth symbole Sk se produit avec la probabilité Pk, où k = 0, 1…k-1.
Laissez le mot de code binaire affecté au symbole Sk, par le codeur ayant une longueur lk, mesuré en bits.
Par conséquent, nous définissons la longueur moyenne du mot de code L du codeur source comme
$$ \ overline {L} = \ displaystyle \ sum \ limits_ {k = 0} ^ {k-1} p_kl_k $$
L représente le nombre moyen de bits par symbole source
Si $ L_ {min} = \: minimum \: possible \: valeur \: of \: \ overline {L} $
ensuite coding efficiency peut être défini comme
$$ \ eta = \ frac {L {min}} {\ overline {L}} $$
Avec $ \ overline {L} \ geq L_ {min} $ nous aurons $ \ eta \ leq 1 $
Cependant, l'encodeur source est considéré comme efficace lorsque $ \ eta = 1 $
Pour cela, la valeur $ L_ {min} $ doit être déterminée.
Faisons référence à la définition, «Étant donné une source discrète d'entropie sans mémoire $ H (\ delta) $, la longueur moyenne du mot de codeL pour tout encodage source est délimité par $ \ overline {L} \ geq H (\ delta) $. "
En termes plus simples, le mot de code (exemple: le code Morse du mot QUEUE est -.- ..-. ..-.) Est toujours supérieur ou égal au code source (QUEUE dans l'exemple). Ce qui signifie que les symboles du mot de code sont supérieurs ou égaux aux alphabets du code source.
Donc avec $ L_ {min} = H (\ delta) $, l'efficacité du codeur source en termes d'entropie $ H (\ delta) $ peut s'écrire
$$ \ eta = \ frac {H (\ delta)} {\ overline {L}} $$
Ce théorème de codage source est appelé noiseless coding theoremcar il établit un codage sans erreur. Il est également appelé commeShannon’s first theorem.
Le bruit présent dans un canal crée des erreurs indésirables entre les séquences d'entrée et de sortie d'un système de communication numérique. La probabilité d'erreur doit être très faible,nearly ≤ 10-6 pour une communication fiable.
Le codage de canal dans un système de communication, introduit une redondance avec une commande, de manière à améliorer la fiabilité du système. Le codage source réduit la redondance pour améliorer l'efficacité du système.
Le codage de canal se compose de deux parties d'action.
Mapping séquence de données entrantes dans une séquence d'entrée de canal.
Inverse Mapping la séquence de sortie du canal en une séquence de données de sortie.
L'objectif final est que l'effet global de la channel noise devrait être minimisé.
La cartographie est réalisée par l'émetteur, à l'aide d'un encodeur, tandis que la cartographie inverse est réalisée par le décodeur dans le récepteur.
Codage des canaux
Considérons un canal discret sans mémoire (δ) avec Entropie H (δ)
Ts indique les symboles que δ donne par seconde
La capacité du canal est indiquée par C
Le canal peut être utilisé pour chaque Tc secondes
Par conséquent, la capacité maximale du canal est C/Tc
Les données envoyées = $ \ frac {H (\ delta)} {T_s} $
Si $ \ frac {H (\ delta)} {T_s} \ leq \ frac {C} {T_c} $ cela signifie que la transmission est bonne et peut être reproduite avec une faible probabilité d'erreur.
En cela, $ \ frac {C} {T_c} $ est le taux critique de capacité du canal.
Si $ \ frac {H (\ delta)} {T_s} = \ frac {C} {T_c} $ alors on dit que le système signale à un taux critique.
Inversement, si $ \ frac {H (\ delta)} {T_s}> \ frac {C} {T_c} $, alors la transmission n'est pas possible.
Par conséquent, le débit maximum de la transmission est égal au débit critique de la capacité du canal, pour des messages fiables sans erreur, qui peuvent avoir lieu, sur un canal discret sans mémoire. Ceci est appelé commeChannel coding theorem.
Le bruit ou l'erreur est le principal problème du signal, ce qui perturbe la fiabilité du système de communication. Error control codingest la procédure de codage effectuée pour contrôler les occurrences d'erreurs. Ces techniques aident à la détection et à la correction des erreurs.
Il existe de nombreux codes de correction d'erreur différents selon les principes mathématiques qui leur sont appliqués. Mais, historiquement, ces codes ont été classés enLinear block codes et Convolution codes.
Codes de blocs linéaires
Dans les codes de blocs linéaires, les bits de parité et les bits de message ont une combinaison linéaire, ce qui signifie que le mot de code résultant est la combinaison linéaire de deux mots de code quelconques.
Considérons quelques blocs de données, qui contiennent kbits dans chaque bloc. Ces bits sont mappés avec les blocs qui ontnbits dans chaque bloc. Icin est supérieur à k. L'émetteur ajoute des bits redondants qui sont(n-k)morceaux. Le rapportk/n est le code rate. Il est désigné parr et la valeur de r est r < 1.
le (n-k) bits ajoutés ici, sont parity bits. Les bits de parité aident à détecter et à corriger les erreurs, ainsi qu'à localiser les données. Dans les données transmises, les bits les plus à gauche du mot de code correspondent aux bits de message, et les bits les plus à droite du mot de code correspondent aux bits de parité.
Code systématique
Tout code de bloc linéaire peut être un code systématique, jusqu'à ce qu'il soit modifié. Par conséquent, un code de bloc non modifié est appelésystematic code.
Voici la représentation du structure of code word, selon leur répartition.

Si le message n'est pas modifié, alors il est appelé comme code systématique. Cela signifie que le cryptage des données ne doit pas changer les données.
Codes de convolution
Jusqu'à présent, dans les codes linéaires, nous avons discuté que le code systématique non modifié est préféré. Ici, les données du totaln bits si transmis, k les bits sont des bits de message et (n-k) les bits sont des bits de parité.
Dans le processus de codage, les bits de parité sont soustraits de l'ensemble des données et les bits de message sont codés. Maintenant, les bits de parité sont à nouveau ajoutés et toutes les données sont à nouveau codées.
La figure suivante cite un exemple de blocs de données et de flux de données, utilisés pour la transmission d'informations.

L'ensemble du processus, indiqué ci-dessus, est fastidieux et présente des inconvénients. L'allocation de tampon est ici un problème majeur, lorsque le système est occupé.
Cet inconvénient est éliminé dans les codes de convolution. Où tout le flux de données reçoit des symboles puis est transmis. Comme les données sont un flux de bits, il n'y a pas besoin de tampon pour le stockage.
Codes de hamming
La propriété de linéarité du mot de code est que la somme de deux mots de code est également un mot de code. Les codes de Hamming sont le type delinear error correcting codes, qui peuvent détecter jusqu'à deux erreurs de bit ou ils peuvent corriger des erreurs d'un bit sans détection d'erreurs non corrigées.
Lors de l'utilisation des codes de martelage, des bits de parité supplémentaires sont utilisés pour identifier une erreur d'un seul bit. Pour passer d'un motif d'un bit à l'autre, quelques bits doivent être modifiés dans les données. Un tel nombre de bits peut être appeléHamming distance. Si la parité a une distance de 2, un basculement d'un bit peut être détecté. Mais cela ne peut pas être corrigé. De plus, aucun retournement de deux bits ne peut être détecté.
Cependant, le code de Hamming est une meilleure procédure que celles discutées précédemment dans la détection et la correction d'erreur.
Codes BCH
Les codes BCH sont nommés d'après les inventeurs Bose, Chaudari et Hocquenghem. Pendant la conception du code BCH, il y a un contrôle sur le nombre de symboles à corriger et par conséquent une correction de bits multiples est possible. Les codes BCH sont une technique puissante dans les codes de correction d'erreur.
Pour tous les nombres entiers positifs m ≥ 3 et t < 2m-1il existe un code binaire BCH. Voici les paramètres d'un tel code.
Longueur de bloc n = 2m-1
Nombre de chiffres de contrôle de parité n - k ≤ mt
Distance minimale dmin ≥ 2t + 1
Ce code peut être appelé t-error-correcting BCH code.
Codes cycliques
La propriété cyclique des mots de code est que tout décalage cyclique d'un mot de code est également un mot de code. Les codes cycliques suivent cette propriété cyclique.
Pour un code linéaire C, si chaque mot de code ie, C = (C1, C2, ...... Cn)à partir de C a un décalage cyclique à droite des composants, il devient un mot de code. Ce décalage de droite est égal àn-1décalages cycliques à gauche. Par conséquent, il est invariant quel que soit le changement. Donc, le code linéaireC, comme il est invariant sous n'importe quel décalage, peut être appelé comme un Cyclic code.
Les codes cycliques sont utilisés pour la correction des erreurs. Ils sont principalement utilisés pour corriger les erreurs doubles et les erreurs de rafale.
Par conséquent, ce sont quelques codes de correction d'erreur, qui doivent être détectés au niveau du récepteur. Ces codes empêchent les erreurs de s'introduire et perturbent la communication. Ils empêchent également le signal d'être capté par des récepteurs indésirables. Il existe une classe de techniques de signalisation pour y parvenir, qui sont discutées dans le chapitre suivant.
Une classe collective de techniques de signalisation est employée avant de transmettre un signal pour fournir une communication sécurisée, connue sous le nom de Spread Spectrum Modulation. Le principal avantage de la technique de communication à spectre étalé est d'éviter les «interférences», qu'elles soient intentionnelles ou non.
Les signaux modulés avec ces techniques sont difficiles à interférer et ne peuvent pas être bloqués. Un intrus sans accès officiel n'est jamais autorisé à les casser. Par conséquent, ces techniques sont utilisées à des fins militaires. Ces signaux à spectre étalé émettent à faible densité de puissance et ont une large diffusion de signaux.
Séquence de pseudo-bruit
Une séquence codée de 1s et 0s avec certaines propriétés d'auto-corrélation, appelées Pseudo-Noise coding sequenceest utilisé dans les techniques à spectre étalé. Il s'agit d'une séquence de longueur maximale, qui est un type de code cyclique.
Signaux à bande étroite et à spectre étalé
Les signaux à bande étroite et à spectre étalé peuvent être facilement compris en observant leur spectre de fréquences comme le montrent les figures suivantes.
Signaux à bande étroite
Les signaux à bande étroite ont la force du signal concentrée comme indiqué dans la figure suivante du spectre de fréquences.
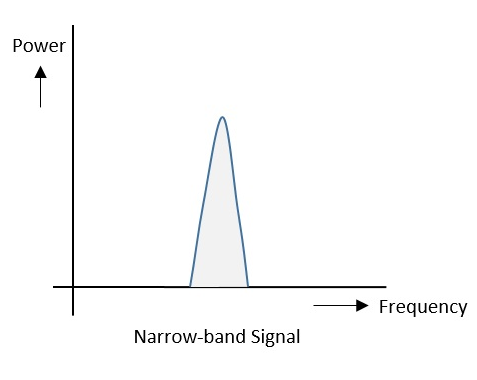
Voici quelques-unes de ses caractéristiques -
- La bande de signaux occupe une gamme étroite de fréquences.
- La densité de puissance est élevée.
- La diffusion d'énergie est faible et concentrée.
Bien que les fonctionnalités soient bonnes, ces signaux sont sujets aux interférences.
Répandre les signaux du spectre
Les signaux à spectre étalé ont la force du signal distribuée comme indiqué dans la figure de spectre de fréquences suivante.
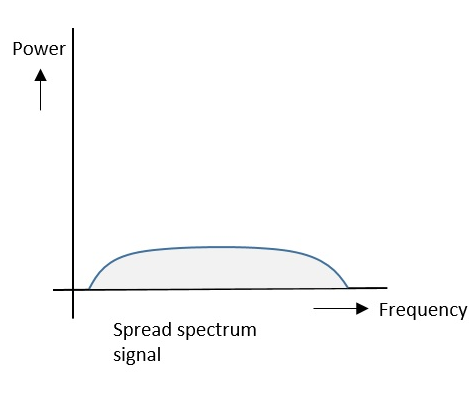
Voici quelques-unes de ses caractéristiques -
- La bande de signaux occupe une large gamme de fréquences.
- La densité de puissance est très faible.
- L'énergie est largement répandue.
Grâce à ces caractéristiques, les signaux à spectre étalé sont très résistants aux interférences ou au brouillage. Étant donné que plusieurs utilisateurs peuvent partager la même bande passante à spectre étalé sans interférer les uns avec les autres, ils peuvent être appelésmultiple access techniques.
FHSS et DSSS / CDMA
Les techniques d'accès multiple à spectre étalé utilisent des signaux qui ont une largeur de bande de transmission d'une amplitude supérieure à la largeur de bande RF minimale requise.
Ce sont de deux types.
- Spectre étalé à sauts de fréquence (FHSS)
- Spectre d'étalement de séquence directe (DSSS)
Spectre étalé à sauts de fréquence (FHSS)
Il s'agit d'une technique de saut de fréquence, dans laquelle les utilisateurs sont amenés à changer les fréquences d'utilisation, de l'une à l'autre dans un intervalle de temps spécifié, donc appelé frequency hopping. Par exemple, une fréquence a été attribuée à l'expéditeur 1 pendant une période donnée. Maintenant, après un certain temps, l'expéditeur 1 saute sur l'autre fréquence et l'expéditeur 2 utilise la première fréquence, qui était auparavant utilisée par l'expéditeur 1. Cela s'appellefrequency reuse.
Les fréquences des données sont sautées de l'une à l'autre afin d'assurer une transmission sécurisée. Le temps passé sur chaque saut de fréquence est appeléDwell time.
Spectre d'étalement de séquence directe (DSSS)
Chaque fois qu'un utilisateur souhaite envoyer des données à l'aide de cette technique DSSS, chaque bit des données utilisateur est multiplié par un code secret, appelé chipping code. Ce code de découpage n'est rien d'autre que le code d'étalement qui est multiplié par le message d'origine et transmis. Le destinataire utilise le même code pour récupérer le message d'origine.
Comparaison entre FHSS et DSSS / CDMA
Les deux techniques à spectre étalé sont populaires pour leurs caractéristiques. Pour avoir une compréhension claire, jetons un coup d'œil à leurs comparaisons.
| FHSS | DSSS / CDMA |
|---|---|
| Plusieurs fréquences sont utilisées | Une seule fréquence est utilisée |
| Difficile de trouver la fréquence de l'utilisateur à tout instant | La fréquence utilisateur, une fois attribuée, est toujours la même |
| La réutilisation des fréquences est autorisée | La réutilisation des fréquences n'est pas autorisée |
| L'expéditeur n'a pas besoin d'attendre | L'expéditeur doit attendre si le spectre est occupé |
| La puissance du signal est élevée | La puissance du signal est faible |
| Plus fort et pénètre à travers les obstacles | Il est plus faible que FHSS |
| Il n'est jamais affecté par les interférences | Il peut être affecté par des interférences |
| C'est moins cher | Il est cher |
| C'est la technique couramment utilisée | Cette technique n'est pas fréquemment utilisée |
Avantages de Spread Spectrum
Voici les avantages du spectre étalé -
- Élimination de la diaphonie
- Meilleure sortie avec intégrité des données
- Effet réduit de l'évanouissement par trajets multiples
- Meilleure sécurité
- Réduction du bruit
- Coexistence avec d'autres systèmes
- Distances opérationnelles plus longues
- Difficile à détecter
- Pas facile à démoduler / décoder
- Difficile de brouiller les signaux
Bien que les techniques à spectre étalé aient été initialement conçues pour des usages militaires, elles sont maintenant largement utilisées à des fins commerciales.