Communication numérique - Codes de ligne
UNE line codeest le code utilisé pour la transmission de données d'un signal numérique sur une ligne de transmission. Ce processus de codage est choisi de manière à éviter le chevauchement et la distorsion du signal comme les interférences entre symboles.
Propriétés du codage de ligne
Voici les propriétés du codage de ligne -
Comme le codage est fait pour faire émettre plus de bits sur un seul signal, la bande passante utilisée est très réduite.
Pour une bande passante donnée, la puissance est utilisée efficacement.
La probabilité d'erreur est très réduite.
La détection d'erreur est effectuée et le bipolaire dispose également d'une capacité de correction.
La densité de puissance est très favorable.
Le contenu de la synchronisation est adéquat.
Longues chaînes de 1s et 0s est évité pour maintenir la transparence.
Types de codage de ligne
Il existe 3 types de codage de ligne
- Unipolar
- Polar
- Bi-polar
Signalisation unipolaire
La signalisation unipolaire est également appelée On-Off Keying ou simplement OOK.
La présence d'impulsion représente un 1 et l'absence d'impulsion représente un 0.
Il existe deux variantes de la signalisation unipolaire -
- Non retour à zéro (NRZ)
- Retour à zéro (RZ)
Non-retour à zéro unipolaire (NRZ)
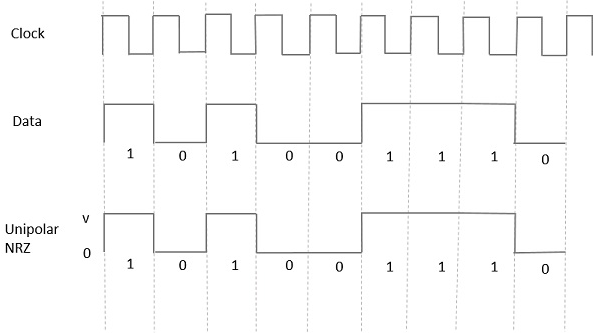
Dans ce type de signalisation unipolaire, un niveau élevé de données est représenté par une impulsion positive appelée Mark, qui a une durée T0égale à la durée du bit de symbole. Une entrée de données faible n'a pas d'impulsion.
La figure suivante illustre clairement cela.
Advantages
Les avantages de Unipolar NRZ sont -
- C'est simple.
- Une bande passante moindre est requise.
Disadvantages
Les inconvénients de la NRZ unipolaire sont:
Aucune correction d'erreur effectuée.
La présence de composants basse fréquence peut provoquer une chute du signal.
Aucune horloge n'est présente.
Une perte de synchronisation est susceptible de se produire (en particulier pour les longues chaînes de 1s et 0s).
Retour unipolaire à zéro (RZ)
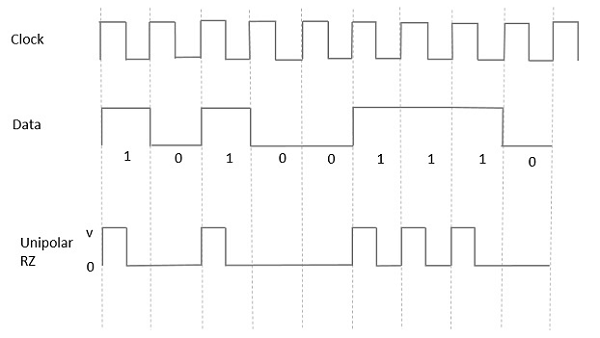
Dans ce type de signalisation unipolaire, un niveau élevé de données, bien que représenté par un Mark pulse, sa durée T0est inférieure à la durée du bit de symbole. La moitié de la durée du bit reste élevée mais elle revient immédiatement à zéro et montre l'absence d'impulsion pendant la moitié restante de la durée du bit.
Il est clairement compris à l'aide de la figure suivante.
Advantages
Les avantages de Unipolar RZ sont -
- C'est simple.
- La raie spectrale présente au débit de symboles peut être utilisée comme horloge.
Disadvantages
Les inconvénients de Unipolar RZ sont -
- Aucune correction d'erreur.
- Occupe deux fois la bande passante comme NRZ unipolaire.
- Le statisme du signal est provoqué aux endroits où le signal est non nul à 0 Hz.
Signalisation polaire
Il existe deux méthodes de signalisation polaire. Ils sont -
- NRZ polaire
- Polar RZ
NRZ polaire
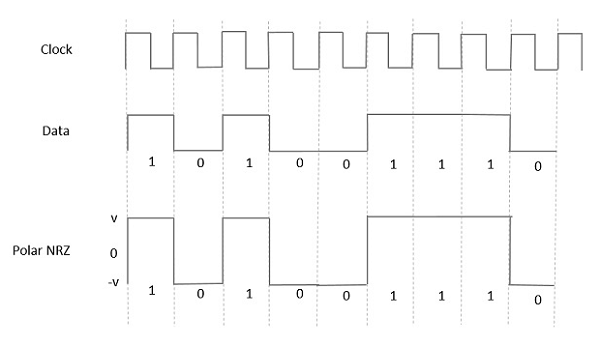
Dans ce type de signalisation polaire, un haut en données est représenté par une impulsion positive, tandis qu'un bas en données est représenté par une impulsion négative. La figure suivante illustre bien cela.
Advantages
Les avantages de Polar NRZ sont -
- C'est simple.
- Aucun composant basse fréquence n'est présent.
Disadvantages
Les inconvénients de Polar NRZ sont -
Aucune correction d'erreur.
Aucune horloge n'est présente.
Le statisme du signal est causé aux endroits où le signal est non nul à 0 Hz.
Polar RZ
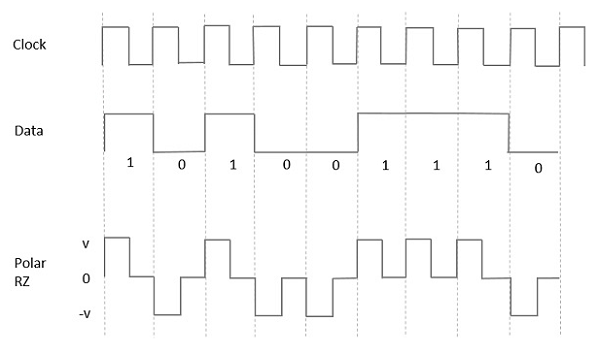
Dans ce type de signalisation polaire, un niveau élevé de données, bien que représenté par un Mark pulse, sa durée T0est inférieure à la durée du bit de symbole. La moitié de la durée du bit reste élevée mais elle revient immédiatement à zéro et montre l'absence d'impulsion pendant la moitié restante de la durée du bit.
Cependant, pour une entrée Low, une impulsion négative représente les données et le niveau zéro reste le même pendant l'autre moitié de la durée du bit. La figure suivante illustre cela clairement.
Advantages
Les avantages de Polar RZ sont -
- C'est simple.
- Aucun composant basse fréquence n'est présent.
Disadvantages
Les inconvénients de Polar RZ sont -
Aucune correction d'erreur.
Aucune horloge n'est présente.
Occupe deux fois la bande passante du Polar NRZ.
Le statisme du signal est causé aux endroits où le signal est différent de zéro à 0 Hz.
Signalisation bipolaire
Il s'agit d'une technique de codage qui a trois niveaux de tension à savoir +, - et 0. Un tel signal est appeléduo-binary signal.
Un exemple de ce type est Alternate Mark Inversion (AMI). Pour un1, le niveau de tension obtient une transition de + à - ou de - à +, ayant alterné 1sêtre de polarité égale. UNE0 aura un niveau de tension nul.
Même dans cette méthode, nous avons deux types.
- NRZ bipolaire
- Bipolaire RZ
À partir des modèles discutés jusqu'à présent, nous avons appris la différence entre NRZ et RZ. Cela se passe de la même manière ici aussi. La figure suivante illustre clairement cela.
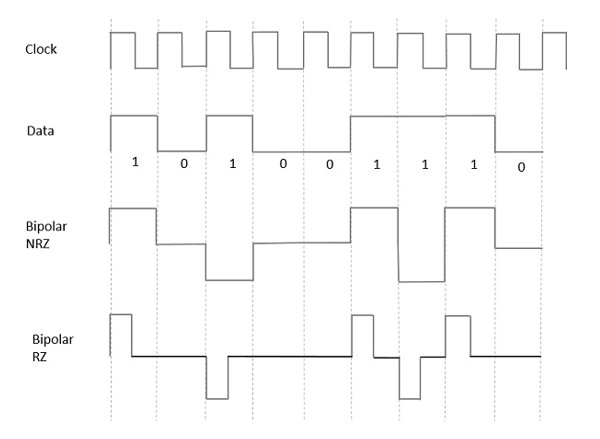
La figure ci-dessus présente les formes d'onde bipolaires NRZ et RZ. La durée de l'impulsion et la durée du bit de symbole sont égales dans le type NRZ, tandis que la durée de l'impulsion est la moitié de la durée du bit de symbole dans le type RZ.
Avantages
Voici les avantages -
C'est simple.
Aucun composant basse fréquence n'est présent.
Occupe une faible bande passante que les schémas NRZ unipolaires et polaires.
Cette technique convient à la transmission sur des lignes couplées en courant alternatif, car le statisme du signal ne se produit pas ici.
Une seule capacité de détection d'erreur est présente dans cela.
Désavantages
Voici les inconvénients -
- Aucune horloge n'est présente.
- De longues chaînes de données entraînent une perte de synchronisation.
Densité spectrale de puissance
La fonction qui décrit comment la puissance d'un signal a été distribuée à différentes fréquences, dans le domaine fréquentiel, est appelée Power Spectral Density (PSD).
PSD est la transformée de Fourier de l'auto-corrélation (similarité entre les observations). Il se présente sous la forme d'une impulsion rectangulaire.
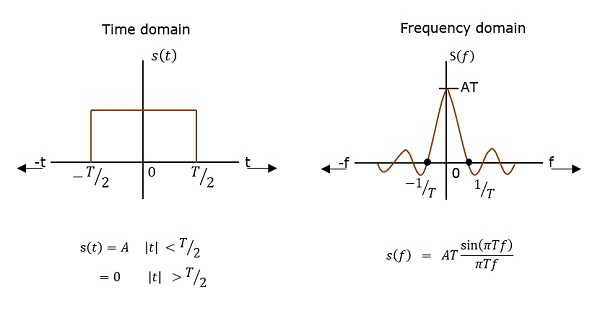
Dérivation PSD
Selon le théorème d'Einstein-Wiener-Khintchine, si la fonction d'auto-corrélation ou la densité spectrale de puissance d'un processus aléatoire est connue, l'autre peut être trouvée exactement.
Par conséquent, pour dériver la densité spectrale de puissance, nous utiliserons l'autocorrélation temporelle $ (R_x (\ tau)) $ d'un signal de puissance $ x (t) $ comme indiqué ci-dessous.
$ R_x (\ tau) = \ lim_ {T_p \ rightarrow \ infty} \ frac {1} {T_p} \ int _ {\ frac {{- T_p}} {2}} ^ {\ frac {T_p} {2}} x (t) x (t + \ tau) dt $
Puisque $ x (t) $ se compose d'impulsions, $ R_x (\ tau) $ peut s'écrire comme
$ R_x (\ tau) = \ frac {1} {T} \ displaystyle \ sum \ limits_ {n = - \ infty} ^ \ infty R_n \ delta (\ tau - nT) $
Où $ R_n = \ lim_ {N \ rightarrow \ infty} \ frac {1} {N} \ sum_ka_ka_ {k + n} $
Apprendre à savoir que $ R_n = R _ {- n} $ pour les signaux réels, nous avons
$ S_x (w) = \ frac {1} {T} (R_0 + 2 \ displaystyle \ sum \ limits_ {n = 1} ^ \ infty R_n \ cos nwT) $
Puisque le filtre d'impulsions a le spectre de $ (w) \ leftrightarrow f (t) $, nous avons
$ s_y (w) = \ milieu F (w) \ milieu ^ 2S_x (w) $
$ = \ frac {\ mid F (w) \ mid ^ 2} {T} (\ displaystyle \ sum \ limits_ {n = - \ infty} ^ \ infty R_ne ^ {- jnwT_ {b}}) $
$ = \ frac {\ mid F (w) \ mid ^ 2} {T} (R_0 + 2 \ displaystyle \ sum \ limits_ {n = 1} ^ \ infty R_n \ cos nwT) $
Par conséquent, nous obtenons l'équation de la densité spectrale de puissance. En utilisant cela, nous pouvons trouver le PSD de divers codes de ligne.