Théorème de codage source
Le Code produit par une source discrète sans mémoire doit être représenté efficacement, ce qui est un problème important dans les communications. Pour cela, il existe des mots de code, qui représentent ces codes sources.
Par exemple, en télégraphie, nous utilisons le code Morse, dans lequel les alphabets sont désignés par Marks et Spaces. Si la lettreE est considéré, qui est le plus utilisé, il est noté “.” Alors que la lettre Q qui est rarement utilisé, est désigné par “--.-”
Jetons un coup d'œil au diagramme.
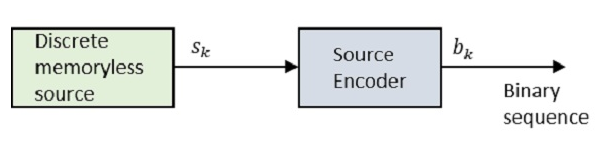
Où Sk est la sortie de la source discrète sans mémoire et bk est la sortie du codeur source qui est représentée par 0s et 1s.
La séquence codée est telle qu'elle est convenablement décodée au niveau du récepteur.
Supposons que la source ait un alphabet avec k symboles différents et que le kth symbole Sk se produit avec la probabilité Pk, où k = 0, 1…k-1.
Laissez le mot de code binaire affecté au symbole Sk, par le codeur ayant une longueur lk, mesuré en bits.
Par conséquent, nous définissons la longueur moyenne du mot de code L du codeur source comme
$$ \ overline {L} = \ displaystyle \ sum \ limits_ {k = 0} ^ {k-1} p_kl_k $$
L représente le nombre moyen de bits par symbole source
Si $ L_ {min} = \: minimum \: possible \: valeur \: of \: \ overline {L} $
ensuite coding efficiency peut être défini comme
$$ \ eta = \ frac {L {min}} {\ overline {L}} $$
Avec $ \ overline {L} \ geq L_ {min} $ nous aurons $ \ eta \ leq 1 $
Cependant, l'encodeur source est considéré comme efficace lorsque $ \ eta = 1 $
Pour cela, la valeur $ L_ {min} $ doit être déterminée.
Faisons référence à la définition, «étant donné une source discrète d'entropie sans mémoire $ H (\ delta) $, la longueur moyenne du mot de codeL pour tout encodage source est délimité par $ \ overline {L} \ geq H (\ delta) $. "
En termes plus simples, le mot de code (exemple: le code Morse du mot QUEUE est -.- ..-. ..-.) Est toujours supérieur ou égal au code source (QUEUE dans l'exemple). Ce qui signifie que les symboles du mot de code sont supérieurs ou égaux aux alphabets du code source.
Donc, avec $ L_ {min} = H (\ delta) $, l'efficacité de l'encodeur source en termes d'entropie $ H (\ delta) $ peut s'écrire comme
$$ \ eta = \ frac {H (\ delta)} {\ overline {L}} $$
Ce théorème de codage source est appelé noiseless coding theoremcar il établit un codage sans erreur. Il est également appelé commeShannon’s first theorem.