Algorithmes de classification - Arbre de décision
Introduction à l'arbre de décision
En général, l'analyse d'arbre de décision est un outil de modélisation prédictive qui peut être appliqué dans de nombreux domaines. Les arbres de décision peuvent être construits par une approche algorithmique qui peut diviser l'ensemble de données de différentes manières en fonction de différentes conditions. Les décisions tress sont les algorithmes les plus puissants qui entrent dans la catégorie des algorithmes supervisés.
Ils peuvent être utilisés pour les tâches de classification et de régression. Les deux principales entités d'un arbre sont les nœuds de décision, où les données sont divisées et partent, où nous avons obtenu le résultat. L'exemple d'un arbre binaire pour prédire si une personne est apte ou inapte, fournissant diverses informations telles que l'âge, les habitudes alimentaires et les habitudes d'exercice, est donné ci-dessous -
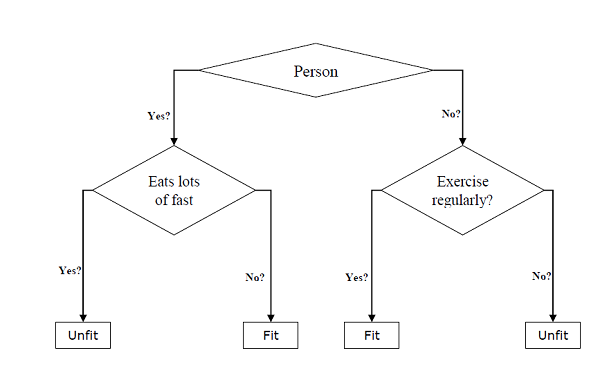
Dans l'arbre de décision ci-dessus, la question concerne les nœuds de décision et les résultats finaux sont les feuilles. Nous avons les deux types d'arbres de décision suivants -
Classification decision trees- Dans ce type d'arbres de décision, la variable de décision est catégorique. L'arbre de décision ci-dessus est un exemple d'arbre de décision de classification.
Regression decision trees - Dans ce type d'arbres de décision, la variable de décision est continue.
Mise en œuvre de l'algorithme d'arbre de décision
Index de Gini
C'est le nom de la fonction de coût qui est utilisée pour évaluer les fractionnements binaires dans le jeu de données et qui fonctionne avec la variable cible catégorielle «Succès» ou «Échec».
Plus la valeur de l'indice de Gini est élevée, plus l'homogénéité est élevée. Une valeur d'indice de Gini parfaite est 0 et la pire est 0,5 (pour le problème à 2 classes). L'indice de Gini pour un fractionnement peut être calculé à l'aide des étapes suivantes -
Tout d'abord, calculez l'indice de Gini pour les sous-nœuds en utilisant la formule p ^ 2 + q ^ 2, qui est la somme du carré de probabilité de succès et d'échec.
Ensuite, calculez l'indice de Gini pour la division en utilisant le score de Gini pondéré de chaque nœud de cette division.
L'algorithme CART (Classification and Regression Tree) utilise la méthode Gini pour générer des fractionnements binaires.
Création fractionnée
Une division comprend essentiellement un attribut dans l'ensemble de données et une valeur. Nous pouvons créer une division dans l'ensemble de données à l'aide des trois parties suivantes -
Part1: Calculating Gini Score - Nous venons de discuter de cette partie dans la section précédente.
Part2: Splitting a dataset- Il peut être défini comme séparant un ensemble de données en deux listes de lignes ayant l'index d'un attribut et une valeur fractionnée de cet attribut. Après avoir récupéré les deux groupes - droite et gauche, à partir de l'ensemble de données, nous pouvons calculer la valeur de la division en utilisant le score de Gini calculé en première partie. La valeur de fractionnement décidera dans quel groupe l'attribut résidera.
Part3: Evaluating all splits- La partie suivante après avoir trouvé le score de Gini et le jeu de données de fractionnement est l'évaluation de toutes les divisions. À cette fin, nous devons d'abord vérifier chaque valeur associée à chaque attribut en tant que fractionnement candidat. Ensuite, nous devons trouver la meilleure répartition possible en évaluant le coût de la répartition. La meilleure division sera utilisée comme nœud dans l'arbre de décision.
Construire un arbre
Comme nous le savons, un arbre a un nœud racine et des nœuds terminaux. Après avoir créé le nœud racine, nous pouvons construire l'arbre en suivant deux parties -
Partie 1: création du nœud terminal
Lors de la création de nœuds terminaux de l'arbre de décision, un point important est de décider quand arrêter la croissance de l'arbre ou créer d'autres nœuds terminaux. Cela peut être fait en utilisant deux critères à savoir la profondeur maximale de l'arbre et les enregistrements de nœuds minimum comme suit -
Maximum Tree Depth- Comme son nom l'indique, il s'agit du nombre maximum de nœuds dans une arborescence après le nœud racine. Il faut arrêter d'ajouter des nœuds terminaux une fois qu'un arbre atteint à la profondeur maximale c'est à dire une fois qu'un arbre a obtenu le nombre maximum de nœuds terminaux.
Minimum Node Records- Il peut être défini comme le nombre minimum de modèles d'apprentissage dont un nœud donné est responsable. Nous devons arrêter d'ajouter des nœuds terminaux une fois que l'arborescence atteint ces enregistrements de nœuds minimum ou en dessous de ce minimum.
Le nœud terminal est utilisé pour faire une prédiction finale.
Partie 2: Fractionnement récursif
Comme nous avons compris quand créer des nœuds terminaux, nous pouvons maintenant commencer à construire notre arbre. Le fractionnement récursif est une méthode pour construire l'arbre. Dans cette méthode, une fois qu'un nœud est créé, nous pouvons créer les nœuds enfants (nœuds ajoutés à un nœud existant) de manière récursive sur chaque groupe de données, générés en fractionnant le jeu de données, en appelant encore et encore la même fonction.
Prédiction
Après avoir construit un arbre de décision, nous devons faire une prédiction à ce sujet. Fondamentalement, la prédiction consiste à naviguer dans l'arbre de décision avec la ligne de données spécifiquement fournie.
Nous pouvons faire une prédiction à l'aide de la fonction récursive, comme ci-dessus. La même routine de prédiction est appelée à nouveau avec les nœuds gauche ou droit enfant.
Hypothèses
Voici quelques-unes des hypothèses que nous faisons lors de la création de l'arbre de décision -
Lors de la préparation des arbres de décision, l'ensemble d'apprentissage est en tant que nœud racine.
Le classificateur d'arbre de décision préfère que les valeurs des caractéristiques soient catégoriques. Si vous souhaitez utiliser des valeurs continues, elles doivent être discrétisées avant la création du modèle.
En fonction des valeurs de l'attribut, les enregistrements sont distribués de manière récursive.
Une approche statistique sera utilisée pour placer des attributs à n'importe quelle position de nœud, à savoir le nœud racine ou le nœud interne.
Implémentation en Python
Exemple
Dans l'exemple suivant, nous allons implémenter le classificateur Arbre de décision sur le diabète indien Pima -
Tout d'abord, commencez par importer les packages Python nécessaires -
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_splitEnsuite, téléchargez le jeu de données iris à partir de son lien Web comme suit -
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
pima = pd.read_csv(r"C:\pima-indians-diabetes.csv", header=None, names=col_names)
pima.head()pregnant glucose bp skin insulin bmi pedigree age label
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1Maintenant, divisez l'ensemble de données en entités et variable cible comme suit -
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variableEnsuite, nous allons diviser les données en train et test split. Le code suivant divisera l'ensemble de données en 70% de données d'entraînement et 30% de données de test -
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)Ensuite, entraînez le modèle à l'aide de la classe DecisionTreeClassifier de sklearn comme suit -
clf = DecisionTreeClassifier()
clf = clf.fit(X_train,y_train)Enfin, nous devons faire des prédictions. Cela peut être fait à l'aide du script suivant -
y_pred = clf.predict(X_test)Ensuite, nous pouvons obtenir le score de précision, la matrice de confusion et le rapport de classification comme suit -
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Production
Confusion Matrix:
[[116 30]
[ 46 39]]
Classification Report:
precision recall f1-score support
0 0.72 0.79 0.75 146
1 0.57 0.46 0.51 85
micro avg 0.67 0.67 0.67 231
macro avg 0.64 0.63 0.63 231
weighted avg 0.66 0.67 0.66 231
Accuracy: 0.670995670995671Visualiser l'arbre de décision
L'arbre de décision ci-dessus peut être visualisé à l'aide du code suivant -
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('Pima_diabetes_Tree.png')
Image(graph.create_png())