Algorithmes de classification - Régression logistique
Introduction à la régression logistique
La régression logistique est un algorithme de classification d'apprentissage supervisé utilisé pour prédire la probabilité d'une variable cible. La nature de la variable cible ou dépendante est dichotomique, ce qui signifie qu'il n'y aurait que deux classes possibles.
En termes simples, la variable dépendante est de nature binaire ayant des données codées soit 1 (signifie succès / oui) ou 0 (signifie échec / non).
Mathématiquement, un modèle de régression logistique prédit P (Y = 1) en fonction de X. C'est l'un des algorithmes ML les plus simples qui peut être utilisé pour divers problèmes de classification tels que la détection de spam, la prédiction du diabète, la détection du cancer, etc.
Types de régression logistique
Généralement, la régression logistique signifie la régression logistique binaire ayant des variables cibles binaires, mais il peut y avoir deux autres catégories de variables cibles qui peuvent être prédites par elle. Sur la base de ce nombre de catégories, la régression logistique peut être divisée en types suivants -
Binaire ou binomial
Dans un tel type de classification, une variable dépendante n'aura que deux types possibles, soit 1 et 0. Par exemple, ces variables peuvent représenter un succès ou un échec, oui ou non, une victoire ou une perte, etc.
Multinomial
Dans un tel type de classification, la variable dépendante peut avoir 3 types non ordonnés ou plus possibles ou les types n'ayant aucune signification quantitative. Par exemple, ces variables peuvent représenter «Type A» ou «Type B» ou «Type C».
Ordinal
Dans un tel type de classification, la variable dépendante peut avoir 3 types ordonnés ou plus possibles ou les types ayant une signification quantitative. Par exemple, ces variables peuvent représenter «mauvais» ou «bon», «très bon», «excellent» et chaque catégorie peut avoir des scores comme 0,1,2,3.
Hypothèses de régression logistique
Avant de plonger dans la mise en œuvre de la régression logistique, nous devons être conscients des hypothèses suivantes à propos du même -
En cas de régression logistique binaire, les variables cibles doivent toujours être binaires et le résultat souhaité est représenté par le facteur niveau 1.
Il ne doit pas y avoir de multi-colinéarité dans le modèle, ce qui signifie que les variables indépendantes doivent être indépendantes les unes des autres.
Nous devons inclure des variables significatives dans notre modèle.
Nous devrions choisir une grande taille d'échantillon pour la régression logistique.
Modèle de régression logistique binaire
La forme la plus simple de régression logistique est la régression logistique binaire ou binomiale dans laquelle la variable cible ou dépendante ne peut avoir que 2 types possibles, soit 1 ou 0. Elle nous permet de modéliser une relation entre plusieurs variables prédictives et une variable cible binaire / binomiale. En cas de régression logistique, la fonction linéaire est essentiellement utilisée comme entrée d'une autre fonction comme dans la relation suivante -
$$ h _ {\ theta} {(x)} = g (\ theta ^ {T} x) ℎ 0≤h _ {\ theta} ≤1 $$Voici la fonction logistique ou sigmoïde qui peut être donnée comme suit -
$$ g (z) = \ frac {1} {1 + e ^ {- z}} ℎ = \ theta ^ {T} $$La courbe sigmoïde peut être représentée à l'aide du graphique suivant. Nous pouvons voir que les valeurs de l'axe y sont comprises entre 0 et 1 et croise l'axe à 0,5.

Les classes peuvent être divisées en positives ou négatives. La sortie relève de la probabilité de classe positive si elle est comprise entre 0 et 1. Pour notre implémentation, nous interprétons la sortie de la fonction d'hypothèse comme positive si elle est ≥0,5, sinon négative.
Nous devons également définir une fonction de perte pour mesurer les performances de l'algorithme en utilisant les poids sur les fonctions, représentés par thêta comme suit -
ℎ = ()
$$ J (\ theta) = \ frac {1} {m}. (- y ^ {T} log (h) - (1 -y) ^ Tlog (1-h)) $$Maintenant, après avoir défini la fonction de perte, notre objectif principal est de minimiser la fonction de perte. Cela peut être fait en ajustant les poids, c'est-à-dire en augmentant ou en diminuant les poids. Avec l'aide de dérivés de la fonction de perte pour chaque poids, nous pourrions savoir quels paramètres devraient avoir un poids élevé et lesquels devraient avoir un poids plus petit.
L'équation de descente de gradient suivante nous indique comment la perte changerait si nous modifiions les paramètres -
$$ \ frac {()} {\ theta_ {j}} = \ frac {1} {m} X ^ {T} (() -) $$Implémentation en Python
Nous allons maintenant implémenter le concept ci-dessus de régression logistique binomiale en Python. À cette fin, nous utilisons un ensemble de données de fleurs multivariées nommé «iris» qui a 3 classes de 50 instances chacune, mais nous utiliserons les deux premières colonnes d'entités. Chaque classe représente un type de fleur d'iris.
Tout d'abord, nous devons importer les bibliothèques nécessaires comme suit -
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasetsEnsuite, chargez le jeu de données iris comme suit -
iris = datasets.load_iris()
X = iris.data[:, :2]
y = (iris.target != 0) * 1Nous pouvons tracer nos données d'entraînement s suit -
plt.figure(figsize=(6, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend();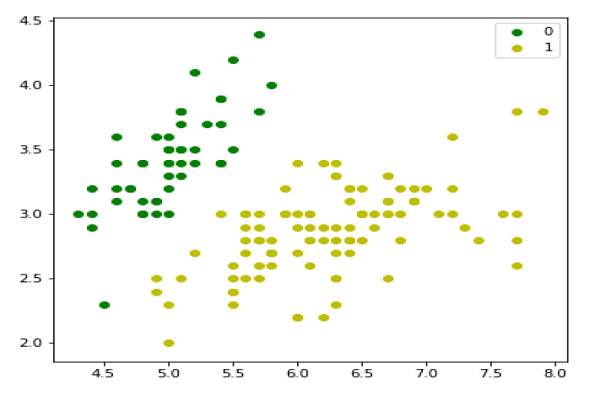
Ensuite, nous définirons la fonction sigmoïde, la fonction de perte et la descente du gradient comme suit -
class LogisticRegression:
def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
self.lr = lr
self.num_iter = num_iter
self.fit_intercept = fit_intercept
self.verbose = verbose
def __add_intercept(self, X):
intercept = np.ones((X.shape[0], 1))
return np.concatenate((intercept, X), axis=1)
def __sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def __loss(self, h, y):
return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
def fit(self, X, y):
if self.fit_intercept:
X = self.__add_intercept(X)Maintenant, initialisez les poids comme suit -
self.theta = np.zeros(X.shape[1])
for i in range(self.num_iter):
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
gradient = np.dot(X.T, (h - y)) / y.size
self.theta -= self.lr * gradient
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
loss = self.__loss(h, y)
if(self.verbose ==True and i % 10000 == 0):
print(f'loss: {loss} \t')Avec l'aide du script suivant, nous pouvons prédire les probabilités de sortie -
def predict_prob(self, X):
if self.fit_intercept:
X = self.__add_intercept(X)
return self.__sigmoid(np.dot(X, self.theta))
def predict(self, X):
return self.predict_prob(X).round()Ensuite, nous pouvons évaluer le modèle et le tracer comme suit -
model = LogisticRegression(lr=0.1, num_iter=300000)
preds = model.predict(X)
(preds == y).mean()
plt.figure(figsize=(10, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend()
x1_min, x1_max = X[:,0].min(), X[:,0].max(),
x2_min, x2_max = X[:,1].min(), X[:,1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = model.predict_prob(grid).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red');
Modèle de régression logistique multinomiale
Une autre forme utile de régression logistique est la régression logistique multinomiale dans laquelle la variable cible ou dépendante peut avoir 3 types non ordonnés ou plus possibles, c'est-à-dire les types n'ayant aucune signification quantitative.
Implémentation en Python
Nous allons maintenant implémenter le concept ci-dessus de régression logistique multinomiale en Python. Pour cela, nous utilisons un ensemble de données de sklearn nommé digit.
Tout d'abord, nous devons importer les bibliothèques nécessaires comme suit -
Import sklearn
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
from sklearn.model_selection import train_test_splitEnsuite, nous devons charger l'ensemble de données numériques -
digits = datasets.load_digits()Maintenant, définissez la matrice de caractéristiques (X) et le vecteur de réponse (y) comme suit -
X = digits.data
y = digits.targetAvec l'aide de la prochaine ligne de code, nous pouvons diviser X et y en ensembles d'entraînement et de test -
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)Créez maintenant un objet de régression logistique comme suit -
digreg = linear_model.LogisticRegression()Maintenant, nous devons entraîner le modèle en utilisant les ensembles d'apprentissage comme suit -
digreg.fit(X_train, y_train)Ensuite, faites les prédictions sur l'ensemble de test comme suit -
y_pred = digreg.predict(X_test)Imprimez ensuite la précision du modèle comme suit -
print("Accuracy of Logistic Regression model is:",
metrics.accuracy_score(y_test, y_pred)*100)Production
Accuracy of Logistic Regression model is: 95.6884561891516À partir de la sortie ci-dessus, nous pouvons voir que la précision de notre modèle est d'environ 96%.